Chapter 9
Complexity of Counting
How do I love thee? Let me count the ways.
I love thee to the depth and breadth and height
My soul can reach.
—Elizabeth Barrett Browning
Informally, the complexity class NP contains the decision problems in which an input instance is accepted if and only if there exists a good witness. The complexity classes PP and BPP contain the problems in which an input instance is accepted if and only if the majority of the witnesses are good. All these problems are just the restricted forms of a more general counting problem: for any input instance, count the number of good witnesses for it. Such counting problems occur very often in practical problems. For instance, for the HAMILTONIAN CIRCUIT problem, one is often interested not only in the existence of a Hamiltonian circuit in a graph but also interested in the total number of different Hamiltonian circuits. In this chapter, we study the complexity of these counting problems and its relation to the complexity of nondeterministic and probabilistic computation. We define two complexity classes, #P and ![]() , of counting problems. The main result of this chapter shows that decision problems in the polynomial-time hierarchy are polynomial-time reducible to counting problems in these complexity classes. We also investigate the relation between the relativized #P and the relativized polynomial-time hierarchy.
, of counting problems. The main result of this chapter shows that decision problems in the polynomial-time hierarchy are polynomial-time reducible to counting problems in these complexity classes. We also investigate the relation between the relativized #P and the relativized polynomial-time hierarchy.
9.1 Counting Class 
Almost all problems we studied so far are decision problems that for an input x ask for answers of a single bit (i.e., YES or NO). In practice, however, we often encounter search problems that for an input x ask for an output y that may be muchlonger than one bit. We have seen in Chapter 2 how to reduce some search problems, particularly the optimization problems, to the corresponding decision problems. Still complexity classes for decision problems, such as NP and BPP, are not adequate to characterize precisely the complexity of search problems. A particularly interesting class of search problems is the class of counting problems related to nondeterministic computation. A decision problem in NP asks, for each input x, whether there exists a witness (or a solution) to x. The corresponding counting problem asks, for any input x, the number of witnesses for x.
Example 9.1
The above example can be extended to other NP-complete problems such as VERTEX COVER and HAMILTONIAN CIRCUIT. In general, for each NP-complete decision problem, there is a corresponding counting problem that is not polynomial-time solvable if ![]() .
.
Example 9.2
Formally, a counting problem is a function f mapping an input ![]() to an integer
to an integer ![]() . The computational model for counting problems is the DTM transducer. A counting problem
. The computational model for counting problems is the DTM transducer. A counting problem ![]() is computable if there exists a DTM transducer M such that for each input
is computable if there exists a DTM transducer M such that for each input ![]() , M(x) outputs integer f(x) in the binary form; it is polynomial-time computable if it is computable by a polynomial-time DTM transducer. In other words, a counting problem f is polynomial-time computable if it is in FP. Note that a function
, M(x) outputs integer f(x) in the binary form; it is polynomial-time computable if it is computable by a polynomial-time DTM transducer. In other words, a counting problem f is polynomial-time computable if it is in FP. Note that a function ![]() must be polynomially length bounded, that is, for all x,
must be polynomially length bounded, that is, for all x, ![]() for some polynomial p. Thus, if a counting problem f is in FP, then
for some polynomial p. Thus, if a counting problem f is in FP, then ![]() for some polynomial p.
for some polynomial p.
Many counting problems such as #SAT and ![]() can easily be defined in terms of NTMs. For any polynomial-time NTM M, we define a counting problem φM as follows: For any
can easily be defined in terms of NTMs. For any polynomial-time NTM M, we define a counting problem φM as follows: For any ![]() ,
, ![]() is the number of accepting computation paths of M(x). As each computation path of M(x), with
is the number of accepting computation paths of M(x). As each computation path of M(x), with ![]() , is of length
, is of length ![]() for some polynomial p, we have the bounds
for some polynomial p, we have the bounds ![]() , where c is a constant bounding the number of nondeterministic choices of M in a nondeterministic move. Thus, all functions φM are polynomial-length bounded. Let
, where c is a constant bounding the number of nondeterministic choices of M in a nondeterministic move. Thus, all functions φM are polynomial-length bounded. Let ![]() denote the class of all polynomial-time NTMs.
denote the class of all polynomial-time NTMs.
Definition 9.3
It is easy to see that each counting function in FP is also in #P. The fundamental question concerning counting problems is whether ![]() .
.
Proposition 9.4
Proof
To understand the power of the counting class #P, we first consider its relation with class NP. From the definition of φM, it is clear that M accepts x if and only if ![]() . Thus, it follows that
. Thus, it follows that ![]() is at least as powerful as NP. Next we consider the relation between
is at least as powerful as NP. Next we consider the relation between ![]() and PP. Assume that
and PP. Assume that ![]() is computed by a polynomial-time PTM M in uniform time t(n), that is, every branch of the computation of M(x) halts in exactly
is computed by a polynomial-time PTM M in uniform time t(n), that is, every branch of the computation of M(x) halts in exactly ![]() moves. Define an NTM M1 that on input x guesses a string y of length
moves. Define an NTM M1 that on input x guesses a string y of length ![]() and accepts x if and only if
and accepts x if and only if ![]() accepts. Then, it follows that
accepts. Then, it follows that ![]() if and only if
if and only if ![]() . Thus,
. Thus, ![]() is at least as powerful as PP.
is at least as powerful as PP.
In the following, we formalize these observations in terms of polynomial-time reducibilities to show that the classes ![]() and PP are equivalent under the polynomial-time Turing reducibility. The notions of function-oracle Turing machines and polynomial-time Turing reducibility on functions have been defined in Chapter 2. Recall that a set A is polynomial-time Turing reducible to a function f, written
and PP are equivalent under the polynomial-time Turing reducibility. The notions of function-oracle Turing machines and polynomial-time Turing reducibility on functions have been defined in Chapter 2. Recall that a set A is polynomial-time Turing reducible to a function f, written ![]() or
or ![]() , if there is a polynomial-time function-oracle TM that computes the characteristic function χA of A when the function f is used as an oracle. Let
, if there is a polynomial-time function-oracle TM that computes the characteristic function χA of A when the function f is used as an oracle. Let ![]() be a class of functions. We let
be a class of functions. We let ![]() denote the class of all sets A that are
denote the class of all sets A that are ![]() -reducible to some functions
-reducible to some functions ![]() .
.
To prepare for this result, we first show that we can restrict ![]() to contain only functions φM that correspond to NTMs that run in polynomial time in uniform time complexity.
to contain only functions φM that correspond to NTMs that run in polynomial time in uniform time complexity.
Proposition 9.5
Proof
Theorem 9.6
Proof
From the above theorem and Theorem 8.16, we have immediately the following relation between ![]() and the polynomial-time hierarchy.
and the polynomial-time hierarchy.
Corollary 9.7
In Section 9.4, we will extend this result to show that the whole polynomial-time hierarchy is contained in ![]() .
.
9.2  -Complete Problems
-Complete Problems
Similar to the notion of NP-completeness, the notion of ![]() -completeness can be used to characterize precisely the complexity of certain counting problems. In this section, we present some
-completeness can be used to characterize precisely the complexity of certain counting problems. In this section, we present some ![]() -complete problems.
-complete problems.
Definition 9.8
We establish the first ![]() -complete problem #SAT from the generic reduction of Cook's theorem.
-complete problem #SAT from the generic reduction of Cook's theorem.
Theorem 9.9
Proof
Let ![]() -SAT be the problem #SAT restricted to 3-CNF Boolean formulas.
-SAT be the problem #SAT restricted to 3-CNF Boolean formulas.
Corollary 9.10
Proof
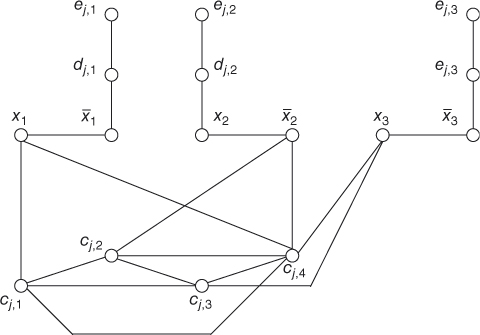
Figure 9.1 The subgraph Gj.
We observe that most reductions used to prove NP-completeness in Section 2.3 either preserve a simple relation between the number of solutions of the two problems or can be easily modified to have this property. Thus, these reductions can be extended into reductions for the corresponding counting problems. In the following, we show that the counting problem for VERTEX COVER is #P-complete. Other #P-complete problems are included in exercises. We let ![]() denote the problem of counting the number of vertex covers of a given size K for a given graph G.
denote the problem of counting the number of vertex covers of a given size K for a given graph G.
Theorem 9.11
Proof
From the above theorem and other similar results (see Exercise 9.1), one might suspect that ![]() -completeness is just a routine extension from NP-complete decision problems to their corresponding counting problems. The following result shows that this is not true: there exist some decision problems in P whose corresponding counting problems are nevertheless
-completeness is just a routine extension from NP-complete decision problems to their corresponding counting problems. The following result shows that this is not true: there exist some decision problems in P whose corresponding counting problems are nevertheless ![]() -complete.
-complete.
We first show that the problem PERM, of computing the permanent of an integer matrix, is ![]() -complete. The permanent of an
-complete. The permanent of an ![]() integer matrix A is
integer matrix A is
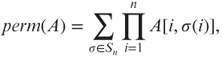
where Sn is the set of all permutations on ![]() . Note that the determinant of a matrix A has a similar form except that a factor of
. Note that the determinant of a matrix A has a similar form except that a factor of ![]() is multiplied to each odd permutation. It is well known that determinants of integer matrices are computable in polynomial time (indeed in NC2). However, no polynomial-time algorithms for permanents are known, despite the similarity between the two problems. The
is multiplied to each odd permutation. It is well known that determinants of integer matrices are computable in polynomial time (indeed in NC2). However, no polynomial-time algorithms for permanents are known, despite the similarity between the two problems. The ![]() -completeness of the function perm shows that the two problems are really quite different as far as their complexity is concerned (assuming
-completeness of the function perm shows that the two problems are really quite different as far as their complexity is concerned (assuming ![]() ).
).
The problem PERM has a number of equivalent formulation. One of them is the problem ![]() of counting the number of perfect matchings (Example 9.2). Another one is the cycle covering problem. Let
of counting the number of perfect matchings (Example 9.2). Another one is the cycle covering problem. Let![]() be a directed graph and
be a directed graph and ![]() a weight function on the edges of G, where
a weight function on the edges of G, where ![]() denotes the set of integers. A collection C of node-disjoint cycles that cover all nodes in G is called a cycle cover of G. The weight of a cycle cover C is the product of the weights of all edges in C. The cycle covering problem is the following:
denotes the set of integers. A collection C of node-disjoint cycles that cover all nodes in G is called a cycle cover of G. The weight of a cycle cover C is the product of the weights of all edges in C. The cycle covering problem is the following:
#CC: Given a directed graph G with a weight function w on edges of G, find the sum of the weights of all cycle covers of G.
For any ![]() integer matrix A, define GA to be the directed graph that has n vertices
integer matrix A, define GA to be the directed graph that has n vertices ![]() and has a weight function
and has a weight function ![]() , that is, the adjacency matrix of GA is A. The following lemma shows a simple relation between the problems
, that is, the adjacency matrix of GA is A. The following lemma shows a simple relation between the problems ![]() and PERM.
and PERM.
Lemma 9.12
Proof
![]()
Theorem 9.13
Proof
Theorem 9.14
Proof
Claim 1. A route Q that is not good has weight 0.
Proof
Claim 2. A good route Q has weight ![]() .
.
Proof
Claim 3. Each interchange Rj has the following properties:
- There is no good route for Rj.
- Let
 be Rj with at least one of
be Rj with at least one of  removed,
removed,  . Then, there is a unique good route for
. Then, there is a unique good route for  .
.
Proof
The following claim finishes the proof of the theorem.
Claim 4. There are exactly s(F) good routes for G.
Proof
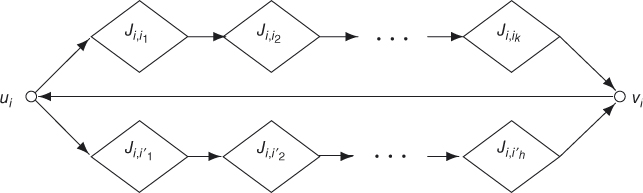
Figure 9.2 The track Ti.
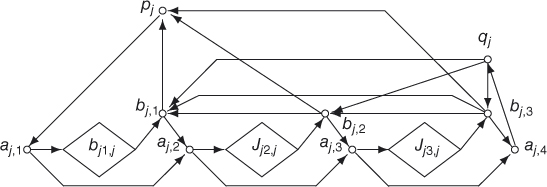
Figure 9.3 The interchange Rj.
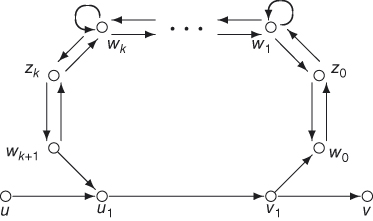
Figure 9.4 Graph Hk.
Now we apply the above result to show that the perfect matching problem is ![]() -complete. As the problem of determining whether a given bipartite graph G has a perfect matching is polynomial-time solvable, this result demonstrates the first
-complete. As the problem of determining whether a given bipartite graph G has a perfect matching is polynomial-time solvable, this result demonstrates the first ![]() -complete problem whose corresponding decision problem is in P.
-complete problem whose corresponding decision problem is in P.
Let ![]() be a bipartite graph in which
be a bipartite graph in which ![]() . Define an
. Define an ![]() (0,1)-matrix MG as follows:
(0,1)-matrix MG as follows:
Then, it is clear that ![]() is exactly the number of perfect matchings in G. Thus, it suffices to prove that the problem of computing the permanents of
is exactly the number of perfect matchings in G. Thus, it suffices to prove that the problem of computing the permanents of ![]() -matrices is
-matrices is ![]() -complete.
-complete.
