Theorem 1.23

Proof

A nondecreasing function f(n) is called superpolynomial if

for all i ≥ 1. For instance, the exponential function 2ⁿ is superpolynomial, and the functions , for k > 1, are also superpolynomial.

Corollary 1.24

Proof

Corollary 1.25

It follows that and .

The above time and space hierarchy theorems can also be extended to nondeterministic time- and space-bounded complexity classes. The proofs, however, are more involved, because acceptance and rejection in NTMs are not symmetric. We only list the simpler results on nondeterministic space-bounded complexity classes, which can be proved by a straightforward diagonalization. For the nondeterministic time hierarchy, see Exercise 1.28.

Theorem 1.26

Proof

In addition to the diagonalization technique, some other proof techniques for separating complexity classes are known. For instance, the following result separating the classes and PSPACE is based on a closure property of PSPACE that does not hold for . Unfortunately, this type of indirect proof techniques is not able to resolve the question of whether or .

Theorem 1.27

Proof

Corollary 1.33

The above results, together with the ones proved in the last section, are the best we know about the relationship among time/space-bounded deterministic/nondeterministic complexity classes. Many other important relations are not known. We summarize in Figure 1.7 the known relations among the most familiar complexity classes. More complexity classes between P and PSPACE will be introduced in Chapters 3, 8, 9, and 10. Complexity classes between LOGSPACE and P will be introduced in Chapter 6.

Exercises

1.1 Let be q natural numbers, and Σ be an alphabet of r symbols. Show that there exist q strings over Σ, of lengths , respectively, which form an alphabet if and only if .

1. 1.2 a. Let c ≥ 0 be a constant. Prove that no pairing function 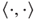exists such that for all , .
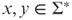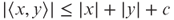2. b. Prove that there exists a pairing function such that (i) for any 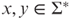, , 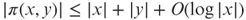(ii) it is polynomial-time computable, and (iii) its inverse function is polynomial-time computable (if 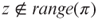, then ).
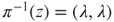3. c. Let 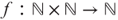be defined by 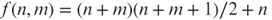. Prove that f is one–one, onto, polynomial-time computable (with respect to the binary representations of natural numbers) and that is polynomial-time computable. (Therefore, f is an efficient pairing function on natural numbers.)

1.3 There are two cities T and F. The residents of city T always tell the truth and the residents of city F always lie. The two cities are very close. Their residents visit each other very often. When you walk in city T you may meet a person who came from city F, and vice versa. Now, suppose that you are in one of the two cities and you want to find out which city you are in. Also suppose that you are allowed to ask a person on the street for only one YES/NO question. What question should you ask? [Hint: You may first design a Boolean function f of two variables, the resident and the city, for your need, and then find a question corresponding to f.]

1.4 How many Boolean functions of n variables are there?

1.5 Assume that f is a Boolean function of more than two variables. Prove that for any minterm p of , there exists a minterm of f containing p as a subterm.

1.6 Design a multi-tape DTM M to accept the language . Show the computation paths of M on inputs and .

1.7 Design a multi-tape NTM M to accept the language for some . Show the computation tree of M on input . What is the time complexity of M?

1.8 Show that the problem of Example 1.2 can be solved by a DTM in polynomial time.

1.9 Give formal definitions of the configurations and the computation of a k-tape DTM.

1.10 Assume that M is a three-tape DTM using tape alphabet . Consider the one-tape DTM M₁ that simulates M as described in Theorem 1.16. Describe explicitly the part of the transition function of M₁ that moves the tape head from left to right to collect the information of the current tape symbols scanned by M.

1.11 Let is an undirected graph, are connected}. Design an NTM M that accepts set C in space . Can you find a DTM accepting C in space ? (Assume that . Then, the input to the machine M is , where if and otherwise.)

1.12 Prove that any finite set of strings belongs to .

1.13 Estimate an upper bound for the number of possible computation histories in the proof of Proposition 1.13.

1.14 A random access machine (RAM) is a machine model for computing integer functions. The memories of a RAM M consists of a one-way read-only input tape, a one-way write-only output tape, and an infinite number of registers named Each square of the input and output tapes and each register can store an integer of an arbitrary size. Let denote the content of the register R_i. An instruction of a RAM may access a register R_i to get its content or it may access the register by the indirect addressing scheme. Each instruction has an integer label, beginning from 1. A RAM begins the computation on instruction with label 1 and halts when it reaches an empty instruction. The following table lists the instruction types of a RAM.

In the above table, we only listed the arguments in the direct addressing scheme. It can be changed to indirect addressing scheme by changing the argument R_i to . For instance, add means to write to R_k. Each instruction can also use a constant argument i instead of R_j. For instance, copy means to write integer i to the register .

1. a. Design a RAM that reads inputs 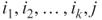and outputs 1 if for some 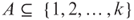and outputs 0 otherwise (cf. Example 1.7).
2. b. Show that for any TM M, there is a RAM M^′ that computes the same function as M. (You need to first specify how to encode tape symbols of the TM M by integers.)
3. c. Show that for any RAM M, there is a TM M^′ that computes the same function as M (with the integer n encoded by the string aⁿ).

1.15 In this exercise, we consider the complexity of RAMs. There are two possible ways of defining the computational time of a RAM M on input x. The uniform time measure counts each instruction as taking one unit of time and so the total runtime of M on x is the number of times M executes an instruction. The logarithmic time measure counts, for each instruction, the number of bits of the arguments involved. For instance, the total time to execute the instruction mult is . The total runtime of M on x, in the logarithmic time measure, is the sum of the instruction time over all instructions executed by M on input x. Use both the uniform and the logarithmic time measures to analyze the simulations of parts (b) and (c) of Exercise 1.14. In particular, show that the notion of polynomial-time computability is equivalent between TMs and RAMs with respect to the logarithmic time measure.

1.16 Suppose that a TM is allowed to have infinitely many tapes. Does this increase its computation power as far as the class of computable sets is concerned?

1.17 Prove Blum's speed-up theorem. That is, find a function such that for any DTM M₁ computing f there exists another DTM M₂ computing f with for infinitely many .

1.18 Prove that if c > 1, then for any ε > 0,

1.19 Prove Theorem 1.15.

1.20 Prove that if f(n) is an integer function such that (i) and (ii) f, regarded as a function mapping aⁿ to , is computable in deterministic time , then f is fully time constructible. [Hint: Use the linear speed-up of Proposition 1.13 to compute the function f in less than f(n) moves, with the output compressed.]

1.21 Prove that if f is fully space constructible and f is not a constant function, then . (We say if there exists a constant c > 0 such that for almost all n ≥ 0.)

1.22 Prove that and are fully space constructible.

1.23 Prove that the question of determining whether a given TM halts in time p(n) for some polynomial function p is undecidable.

1.24 Prove that for any one-worktape DTM M that uses space s(n), there is a one-worktape DTM M^′ with such that it uses space s(n) and its tape head never moves to the left of its starting square.

1.25 Recall that (k iterations of on n) . Let k > 0 and t₂ be a fully time-constructible function. Assume that

Prove that there exists a language L that is accepted by a k-tape DTM in time but not by any k-tape DTM in time .

1.26 Prove that .

1. 1.27 a. Prove Theorem 1.26 (cf. Theorems 1.30 and 1.32).
2. b. Prove that for any integer k ≥ 1 and any rational ε > 0, .

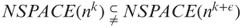1. 1.28 a. Prove that .
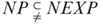2. b. Prove that 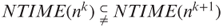for any k ≥ 1.

1.29 Prove that and .

1.30 A set A is called a tally set if for some symbol a. A set A is called a sparse set if there exists a polynomial function p such that for all n ≥ 1. Prove that the following are equivalent:

1. .
2. All tally sets in NP are actually in P.
3. All sparse sets in NP are actually in P. (Note: The above implies that if then .)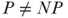

1.31 (BUSY BEAVER) In this exercise, we show the existence of an r.e., nonrecursive set without using the diagonalization technique. For each TM M, we let denote the length of the codes for M. We consider only one-tape TMs with a fixed alphabet . Let and . That is, f(x) is the size of the minimum TM that outputs x on the input λ, and g(m) is the least x that is not printable by any TM M of size on the input λ. It is clear that both f and g are total functions.

1. Prove that neither f nor g is a recursive function.
2. Define . Apply part (a) above to show that A is r.e. but is not recursive.

1.32 (BUSY BEAVER, time-bounded version) In this exercise, we apply the busy beaver technique to show the existence of a set computable in exponential time but not in polynomial time.

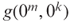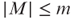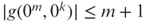1. Let be the least that is not printable by any TM M of size on input λ in time . It is easy to see that , and hence, g is polynomial length bounded. Prove that 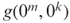is computable in time 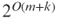but is not computable in time polynomial in .
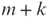2. Can you modify part (a) above to prove the existence of a function that is computable in subexponential time (e.g., ) but is not polynomial-time computable?

1.33 Assume that an NTM computes the characteristic function χ_A of a set A in polynomial time, in the sense of Definition 1.8. What can you infer about the complexity of set A?

1.34 In the proof of Theorem 1.30, the predicate reach was solved by a deterministic recursive algorithm. Convert it to a nonrecursive algorithm for the predicate reach that only uses space .

1.35 What is wrong if we use the following simpler algorithm to compute N_k in the proof of Theorem 1.32?

For each k, to compute N_k, we generate each configuration one by one and, for each one, nondeterministically verify whether (by machine M₁), and increments the counter for N_k by one if holds.

1.36 In this exercise, we study the notion of computability of real numbers. First, for each , we let denote its binary expansion, and for each , let if x ≥ 0, and if x < 0. An integer is represented as . A rational number with , b ≠ 0, and has a unique representation over alphabet : . We write ( and ) to denote both the set of natural numbers (integers and rational numbers, respectively) and the set of their representations. We say a real number x is Cauchy computable if there exist two computable functions and satisfying the property C_f,m: . A real number x is Dedekind computable if the set is computable. A real number x is binary computable if there is a computable function , with the property for all n > 0, such that

where if x ≥ 0 and if x < 0. (The function b_x is not unique for some x, but notice that for such x, both the functions b_x are computable.) A real number x is Turing computable if there exists a DTM M that on the empty input prints a binary expansion of x (i.e., it prints the string followed by the binary point and then followed by the infinite string ).

Prove that the above four notions of computability of real numbers are equivalent. That is, prove that a real number x is Cauchy computable if and only if it is Dedekind computable if and only if it is binary computable if and only if it is Turing computable.

1.37 In this exercise, we study the computational complexity of a real number. We define a real number x to be polynomial-time Cauchy computable if there exist a polynomial-time computable function and a polynomial function , satisfying C_f,m, where f being polynomial-time computable means that f(n) is computable by a DTM in time p(n) for some polynomial p (i.e., the input n is written in the unary form). We say x is polynomial-time Dedekind computable if L_x is in P. We say x is polynomial-time binary computable if b_x, restricted to inputs n > 0, is polynomial-time computable, assuming that the inputs n are written in the unary form.

Prove that the above three notions of polynomial-time computability of real numbers are not equivalent. That is, let P_C (P_D, and P_b) denote the class of polynomial-time Cauchy (Dedekind and binary, respectively) computable real numbers. Prove that .

Historical Notes

McMillan's theorem is well known in coding theory; see, for example, Roman (1992). TMs were first defined by Turing (1936, 1937). The equivalent variations of TMs, the notion of computability, and the Church–Turing Thesis are the main topics of recursive function theory; see, for example, Rogers (1967) and Soare (1987). Kleene (1979) contains an interesting personal account of the history. The complexity theory based on TMs was developed by Hartmanis and Stearns (1965), Stearns, Hartmanis, and Lewis (1965) and Lewis, Stearns, and Hartmanis (1965). The tape compression theorem, the linear speed-up theorem, the tape-reduction simulations (Corollaries 1.14–1.16) and the time and space hierarchy theorems are from these works. A machine-independent complexity theory has been established by Blum (1967). Blum's speed-up theorem is from there. Cook (1973a) first established the nondeterministic time hierarchy. Seiferas (1977a, 1977b) contain further studies on the hierarchy theorems for nondeterministic machines. The indirect separation result, Theorem 1.27, is from Book (1974a). The identification of P as the class of feasible problems was first suggested by Cobham (1964) and Edmonds (1965). Theorem 1.30 is from Savitch (1970). Theorem 1.32 was independently proved by Immerman (1988) and Szelepcsényi (1988). Hopcroft et al. (1977) and Paul et al. (1983) contain separation results between , , and . Context-sensitive languages and grammars are major topics in formal language theory; see, for example, Hopcroft and Ullman (1979).

RAMs were first studied in Shepherdson and Sturgis (1963) and Elgot and Robinson (1964). The improvements over the time hierarchy theorem, including Exercises 1.25 and 1.26, can be found in Paul (1979) and Fürer (1984). Exercise 1.30 is an application of the Translation Lemma of Book (1974b); see Hartmanis et al. (1983). The busy beaver problems (Exercises 1.31 and 1.32) are related to the notion of the Kolmogorov complexity of finite strings. The arguments based on the Kolmogorov complexity avoids the direct use of diagonalization. See Daley (1980) for discussions on the busy beaver proof technique, and Li and Vitányi (1997) for a complete treatment of the Kolmogorov complexity. Computable real numbers were first studied by Turing (1936) and Rice (1954). Polynomial-time computable real numbers were studied in Ko and Friedman (1982) and Ko (1991a).