Chapter 3
The Polynomial-Time Hierarchy and Polynomial Space
One thing nice about space is that it keeps on going ...
—Willem de Kooning
We study complexity classes beyond the class NP. First, the polynomial-time hierarchy of complexity classes is introduced based on nondeterministic oracle machines. This hierarchy lies between the class P and the class PSPACE, and the class NP is the first level of the hierarchy. Characterizations of these complexity classes in terms of alternating quantifiers and alternating Turing machines (ATMs) are proven. Finally, we present some natural complete problems for this hierarchy and for complexity classes PSPACE and EXP.
3.1 Nondeterministic Oracle Turing Machines
We have defined in Chapter 2 the notions of polynomial-time Turing reducibility and oracle TMs, and have seen that many optimization problems, when formulated in the search problem form, are solvable in polynomial time relative to a set in NP. We now extend this notion to nondeterministic oracle TMs and study problems that are solvable in nondeterministic polynomial time relative to sets in NP.
A nondeterministic (function-)oracle Turing machine (oracle NTM) is an NTM equipped with an additional query tape and two additional states: the query state and the answer state. The computation of an oracle NTM is similar to that of an oracle DTM, except that at each nonquery state an oracle NTM can make a nondeterministic move. We require that the query step of the computation be a deterministic move determined by the oracle. Let M be an oracle NTM and f an oracle function. We write 
to denote the computation of M on input x, using f as the oracle function (note that this is a computation tree). If the oracle function is a characteristic function of a set A, we say M is a set-oracle NTM and write MA to denote Mf, and write 
to denote the set of strings accepted by MA.
The time complexity of a set-oracle NTM is also defined similar to that of a set-oracle DTM. In particular, the actions from the query state to the answer state count as only one step. For any fixed oracle set A, we let 
be the length of the shortest accepting computation path of 
and 
accepts x}). For a set-oracle NTM M, we say 
is bounded by a function g(n), if for all oracle sets A, 
. An oracle NTM M is a polynomial-time oracle NTM if 
is bounded by a polynomial function p. Let A be a set and 
be a complexity class. We let NPA denote the class of sets accepted by polynomial-time oracle NTMs relative to the oracle A, and let 
(or, 
) denote the class of sets accepted by polynomial-time oracle NTMs using an oracle 
(i.e., 
).
Proposition 3.1
Let A≤NPTB denote that A∈NPB. It is provable that 
does not have the transitivity property and, hence, is not really a reducibility (see Exercise 4.13). Thus, property (d) above does not fully extend to the case when 
. In Exercise 3.1, we give a partial extension of this property.
Proposition 3.2
Proof
3.2 Polynomial-Time Hierarchy
The polynomial-time hierarchy is the polynomial analog of the arithmetic hierarchy in recursion theory (Rogers, 1967). It can be defined inductively by oracle NTMs.
Definition 3.3
Thus, 
, 
, 
, and so on. It is easy to verify that these classes form a hierarchy.
Proposition 3.4
Proof
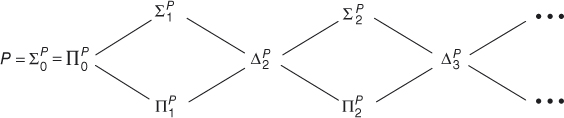
Figure 3.1 The polynomial-time hierarchy.
Based on the above proposition, we show in Figure 3.1 the basic structure of the polynomial-time hierarchy. To further understand the structure of the polynomial-time hierarchy, we first extend Theorem 2.1 to a characterization of the polynomial-time hierarchy in terms of the polynomial-length-bounded quantifiers.
First, we observe some closure properties of the polynomial-time hierarchy under the Boolean operations.
Lemma 3.5
Proof
The following lemma can be proved in a similar way.
Lemma 3.6
In the following, we say a predicate 
of n variables 
is a 
-predicate (or a 
-predicate), where k ≥ 0, if the set 
is in 
(or, respectively, in 
). Lemma 3.5 then states that if Q1 and Q2 are two 
-predicates (or, 
-predicates), then 
and 
are also 
-predicates (or, 
-predicates), and 
is a 
-predicate (or, respectively, 
-predicate).
Lemma 3.7
Proof
Theorem 3.8
Proof
Using the above characterization, we can prove that if any two levels of the polynomial-time hierarchy collapses, then the whole hierarchy collapses to that level.
Theorem 3.9
Proof
Corollary 3.10
Proof
The above corollary reveals an interesting property of the polynomial-time hierarchy; namely, if any two levels of the hierarchy collapses into one, then the whole hierarchy collapses to that level. Still, the main question of whether the hierarchy is properly infinite is not known. Many questions about relations between complexity classes are often reduced to the question of whether the polynomial-time hierarchy collapses. Notice that the assumption of the polynomial-time hierarchy not collapsing is stronger than the assumption of 
. Thus, when the assumption of 
is not sufficient to establish the intractability of a problem A, this stronger assumption might be useful. We will present some applications in Chapters 6 and 10.
3.3 Complete Problems in PH
We have proved in Example 2.20 that the problem EXACT-CLIQUE is in 
, and it is 
-hard for NP. Therefore, it is 
-complete for 
, because all problems in 
are 
-reducibleto a problem in NP. For most NP-complete optimization problems, it can be easily shown that the corresponding version of the decision problem of determining whether a given integer K is the size of the optimum solutions is 
-complete for 
.
In addition to complete problems in 
, there are also natural problems complete for the classes in the higher levels of the polynomial-time hierarchy. First, we show that the generic NP-complete problem BOUNDED HALTING PROBLEM, or BHP, has relativized versions that are complete for classes 
for k > 1. Let A be an arbitrary set.
BHP relative to set A (BHPA): Given an oracle NTM M, an input w, and a time bound t, written in the unary form 0t, determine whether MA accepts w in t moves.
First, a simple modification of the universal NTM yields a universal oracle NTM Mu that can simulate any oracle NTM in polynomial time. Thus, 
. Next, we observe that the reduction in Theorem 2.11 from any set 
to BHP relativizes. So, for any set A, BHPA is 
-complete for the class NPA.
Now, define 
, and for k ≥ 0, 
.
Lemma 3.11
Proof
Theorem 3.12
Proof
Next, for natural complete problems, we show that for each k ≥ 1, there is a generalization of the problem SAT that is complete for the class 
. In the following, we write 
to mean a Boolean assignment τ defined on variables in the set X. Let k ≥ 1.
SATk: Given k sets of variables, and a Boolean formula F over variables in
, determine whether it is true that
where Qk denotes 
if k is odd, and it denotes 
if k is even.
In the above, 
denotes that the combined assignment 
satisfies F.
Theorem 3.13
Proof
Again, for the reductions from SATk to other 
-complete problems, the restricted forms of SATk would be more useful. Recall that a 3-CNF formula is a formula in CNF such that each clause has exactly three literals defined from three distinct variables. A 3-DNF (3-disjunctive normal form) formula is a formula in DNF such that each term has exactly three literals defined from three distinct variables.
We let 3-CNF-SATk (3-DNF-SATk) denote the problem of determining whether a given 3-CNF (3-DNF, respectively) formula F satisfies (3.3). We also let 3-CNF-TAUk (3-DNF-TAUk) denote the problem of determining whether a given 3-CNF (3-DNF, respectively) formula F satisfies
where 
if k is odd, and 
if k is even.
Corollary 3.14
Proof
In addition to SATk, there are a few natural problems known to be complete for the complexity classes in the first three levels of the polynomial-time hierarchy but very few known to be complete for classes in the higher levels. In the following, we show a generalization of the maximum clique problem to be 
-complete for 
. Some other examples are included in exercises.
We say that a graph 
is k-colored if it is associated with a function 
. The Ramsey number Rk, for each integer k > 0, is the minimum integer n such that every two-colored complete graph G of size n contains a monochromatic clique Q of size k (i.e., all edges between two vertices in Q are of the same color). The existence of the number Rk for each k > 0 is the famous Ramsey theorem. A generalized form of the question of computing the Ramsey numbers is the following: