Chapter 4
Structure of NP
In order to understand the difficulty of solving the P versus NP problem, we study in this chapter the internal structure of the complexity class NP. We demonstrate some natural problems as candidates of incomplete problems in NP–P and study the notion of one-way functions. We also introduce the notion of relativization to help us understand the possible relations between subclasses of NP. One of the main proof techniques used in this study is stage-construction diagonalization, which has been used extensively in recursion theory.
4.1 Incomplete Problems in NP
We have seen many NP-complete problems in Chapter 2. Many natural problems in NP turn out to be NP-complete. There are, however, a few interesting problems in NP that are not likely to be solvable in deterministic polynomial time but also are not known to be NP-complete. The study of these problems is thus particularly interesting, because it not only can classify the inherent complexity of the problems themselves but can also provide a glimpse of the internal structure of the class NP. We start with some examples.
Example 4.1
There are many number-theoretic problems in NP that are neither known to be NP-complete nor known to be in P. We list three of them that have major applications in cryptography. An integer ![]() is called a quadratic residue modulo n if
is called a quadratic residue modulo n if ![]() for some
for some ![]() . We write
. We write ![]() to denote this fact.
to denote this fact.
Example 4.2
The above examples suggest that there are problems in NP–P that are not complete for NP. However, we do not even know that such sets exist at all. In the following we show, in an abstract form, that such sets indeed exist, if ![]() . To prepare for the proof of the theorem, we recall from Chapter 1 that there exists an effective enumeration
. To prepare for the proof of the theorem, we recall from Chapter 1 that there exists an effective enumeration ![]() ofall polynomial-time DTMs, as well as an effective enumeration
ofall polynomial-time DTMs, as well as an effective enumeration ![]() of all polynomial-time oracle DTMs. For the following theorem, we need an even stronger property of these enumerations, that is, the enumerations can be done in polynomial time in the sense that the functions
of all polynomial-time oracle DTMs. For the following theorem, we need an even stronger property of these enumerations, that is, the enumerations can be done in polynomial time in the sense that the functions ![]() [code of Mi] and
[code of Mi] and ![]() [code of Ni] are polynomial-time computable. It is easy to see that this stronger property follows from our enumeration method in Section 1.5. Also, in the following theorem, we let
[code of Ni] are polynomial-time computable. It is easy to see that this stronger property follows from our enumeration method in Section 1.5. Also, in the following theorem, we let ![]() denote the set difference between two sets A and B, that is,
denote the set difference between two sets A and B, that is, ![]() .
.
Theorem 4.3
Proof
The above proof method is called the delayed diagonalization, because the diagonalization requirements ![]() and
and ![]() are satisfied by a search process that always halts but the amount of time for the search is not known in advance.
are satisfied by a search process that always halts but the amount of time for the search is not known in advance.
The following theorem, an analog of Post's problem in the classical recursion theory, reveals further structural properties of languages in NP. It can be proved using the technique of delayed diagonalization. We leave its proof as an exercise.
Theorem 4.4
4.2 One-Way Functions and Cryptography
One-way functions are a fundamental concept in cryptography, having a number of important applications, including public-key cryptosystems, pseudorandom generators, and digital signatures. Intuitively, a one-way function is a function that is easy to compute but its inverse is hard to compute. Thus it can be applied to develop cryptosystems that need easy encoding but difficult decoding. If we identify the intuitive notion of “easiness” with the mathematical notion of “polynomial-time computability,” then one-way functions are subproblems of NP, because the inverse function of a polynomial-time computable function is computable in polynomial-time relative to an oracle in NP, assuming that the functions are polynomially honest. Indeed, all problems in NP may be viewed as one-way functions.
Example 4.5
Strictly speaking, function ![]() is, however, not really a one-way function because it is not a one-to-one function and its inverse is really a multivalued function. In the following, we define one-way functions for one-to-one functions. We say that a function
is, however, not really a one-way function because it is not a one-to-one function and its inverse is really a multivalued function. In the following, we define one-way functions for one-to-one functions. We say that a function ![]() is polynomially honest if there is a polynomial function q such that for each
is polynomially honest if there is a polynomial function q such that for each ![]() ,
, ![]() and
and ![]() .
.
Definition 4.6
The above definition did not define the notion of inverse function of f, because f is not necessarily a surjection. We may arbitrarily define the inverse function![]() of a one-to-one function f to be
of a one-to-one function f to be
and have the following equivalent definition.
Proposition 4.7
Proof
Following the example ![]() , it is easy to see that if
, it is easy to see that if ![]() , then one-way functions do not exist. Indeed, the complexity of weak one-way functions can be characterized precisely by a subclass UP of NP.
, then one-way functions do not exist. Indeed, the complexity of weak one-way functions can be characterized precisely by a subclass UP of NP.
Definition 4.8
It is clear that ![]() . The following characterization of UP is a simple extension of Theorem 2.1.
. The following characterization of UP is a simple extension of Theorem 2.1.
Proposition 4.9
Proposition 4.10
Proof
A one-way function f satisfying the conditions of Definition 4.6 is called a weak one-way function because its inverse is not computable in polynomial time in the very weak worst-case complexity measure. That is, for every polynomial-time computable function g attempting to compute the inverse of f, there are infinitely many instances ![]() , such that
, such that ![]() for all i ≥ 1. However, this function g could be a very good approximation to
for all i ≥ 1. However, this function g could be a very good approximation to ![]() in the sense that such errors occur only on some very sparsely distributed instances
in the sense that such errors occur only on some very sparsely distributed instances ![]() . In the applications of cryptography, a cryptosystem based on such a one-way function is not secure because the approximation function g allows a fast decoding for a large portion of the input instances. Instead, stronger one-way functions whose inverses are hard to compute for the majority of input instances are needed for a secure cryptosystem. We formulate this notion in the following. We only consider functions defined on alphabet {0,1}.
. In the applications of cryptography, a cryptosystem based on such a one-way function is not secure because the approximation function g allows a fast decoding for a large portion of the input instances. Instead, stronger one-way functions whose inverses are hard to compute for the majority of input instances are needed for a secure cryptosystem. We formulate this notion in the following. We only consider functions defined on alphabet {0,1}.
Definition 4.11
In other words, a function f is strongly one way if any polynomial-time function approximating its inverse succeeds only on a small (or negligible) amount of input instances.1 As this notion of strong one-way functions is much stronger than that of Definition 4.6, it is questionable whether strong one-way functions really exist. Most researchers in cryptography, however, believe that many strong one-way functions do exist. Several natural candidates for strong one-way functions have been found in number-theoretic problems. In particular, the problems FACTOR and SQRT are believed to be so hard to solve that any attack to them can only solve a negligible portion of the input instances. That is, the functions multiplication and square modulo an integer are candidates of strong one-way functions.2,3
Corresponding to the notion of strong one-way functions, there are some natural decision problems that are also considered difficult to solve even for a small portion of the input instances. The following definition captures this notion in the spirit of Definition 4.11.
Definition 4.12
For instance, let n be an integer that is a product of two prime numbers, p and q. Then, in general, it is considered as an extremely difficult problem to determine whether a given integer x, ![]() , is in QRn. In theoretical cryptography, it is often assumed that sets QRn are strongly unpredictable in the sense that there exists an infinite set S of positive integers such that for any polynomial-time computable function
, is in QRn. In theoretical cryptography, it is often assumed that sets QRn are strongly unpredictable in the sense that there exists an infinite set S of positive integers such that for any polynomial-time computable function ![]() and any polynomial function p,
and any polynomial function p,
for almost all ![]() . (See an application in Exercise 4.8.)
. (See an application in Exercise 4.8.)
In the rest of this section, we present a public-key cryptosystem based on the assumption that the function multiplication is a strong one-way function. We first introduce some terminology for public-key cryptosystems. In a public-key cryptosystem, a sender S needs to send amessage TP to a receiver R via a communication channel that is open to the public (hence, not secure), and yet the system needs to protect the message from the unauthorized users of the system. To ensure the security, the sender S first applies an encryption algorithm E to map the message TP (the plaintext) to an encrypted message TC (the ciphertext) and then sends the message TC to the receiver R. The receiver R then applies a decryption algorithm D to map TC back to TP. Usually, all users in the system use the same encryption and decryption algorithms but each user uses different parameters when applying these algorithms. That is, the encryption and decryption algorithms compute functions of two parameters: ![]() and
and ![]() . The parameters KE and KD are called the encryption key and the decryption key, respectively. Each pair of users S and R may be required to set up their own keys for communication. The transmission of the message is illustrated in Figure 4.1.
. The parameters KE and KD are called the encryption key and the decryption key, respectively. Each pair of users S and R may be required to set up their own keys for communication. The transmission of the message is illustrated in Figure 4.1.
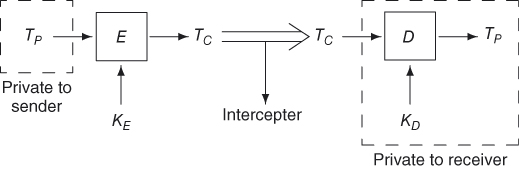
Figure 4.1 A public-key cryptosystem.
In a private-key cryptosystem, both keys KE and KD are kept secret from the public. Each pair of users S and R first, through some other secret channel, develops the encryption and decryption keys and keeps them to themselves. Such a system is secure if it is hard to compute a plaintext from the ciphertext alone.
In a public-key cryptosystem, each user R establishes his/her own pair of keys KE and KD and makes the encryption key KE open to the public but keeps the decryption key KD secret to him/herself. As the encryption key KE is known not only to the sender S but also to all other users, the system is secure only if it is hard to compute the plaintext from the ciphertext and the encryption key. In particular, the decryption key must be hard to compute from the encryption key. In other words, the function ![]() needs to satisfy the following conditions:
needs to satisfy the following conditions:
- f is easy to compute;
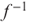 is hard to compute even if KE is known; and
is hard to compute even if KE is known; and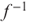 becomes easy to compute if KD is available.
becomes easy to compute if KD is available.
Such a function is called a trapdoor one-way function. So, a one-way function f can be applied to public-key cryptosystems only if it is also a trapdoor function (i.e., to satisfy condition (3) above).
The Rivest–Shamir–Adleman (RSA) cryptosystem is based on the one-way function exponentiation modulo an integer. In this system, each pair of keys KE and KD is selected as follows: First, find two distinct prime numbers p,q, and let ![]() . Next, find a pair of integers
. Next, find a pair of integers ![]() such that
such that
where ![]() is the Euler function, that is,
is the Euler function, that is, ![]() is the number of positive integers x with
is the number of positive integers x with ![]() . Note that for
. Note that for ![]() ,
, ![]() . Let
. Let![]() and
and ![]() . The encryption function E and the decryption function D are defined as follows:
. The encryption function E and the decryption function D are defined as follows:
The following lemma shows that the above functions E and D are inverses of each other.
Lemma 4.13
Proof
To see whether the RSA system is a good public-key cryptosystem, we need to verify whether the encryption function is indeed a trapdoor one-way function. First, we observe that if p,q are known, then the integers e and d satisfying (4.1) are easy to find and, hence, the system is easy to set up. To find the pair (e,d), we first select a prime number e between ![]() and
and ![]() . As
. As ![]() , we have
, we have ![]() , and so e is relatively prime to
, and so e is relatively prime to ![]() . Then, using the Euclidean algorithm, we can find the integer d such that
. Then, using the Euclidean algorithm, we can find the integer d such that ![]() (see, e.g., Knuth (1981)). Next, it is well known that exponentiation function
(see, e.g., Knuth (1981)). Next, it is well known that exponentiation function ![]() can be computed using
can be computed using ![]() modulo multiplications by a simple dynamic programming algorithm. Thus, both E and D are easy to compute. So it is left to determine how hard it is to compute the decryption key
modulo multiplications by a simple dynamic programming algorithm. Thus, both E and D are easy to compute. So it is left to determine how hard it is to compute the decryption key ![]() from the encryption key (the public key)
from the encryption key (the public key) ![]() . If the factors p and q of n are known, then
. If the factors p and q of n are known, then ![]() is known and the integer d can be found easily from e. Thus, the security of the RSA system depends on the hardness of factoring an integer into two primes. Conversely, suppose that integer factoring is known to be an intractable problem. Does it mean that the RSA system is secure? In other words, if we have a fast algorithm breaking the RSA system, do we then have a fast factoring algorithm? The answer is yes if we make some modification on the above scheme (see Rabin (1979)). Thus, the complexity of breaking the (modified) RSA system is equivalent to the complexity of factoring the products of two primes, and the RSA system is considered secure, assuming that the function multiplication is a strong one-way function.4
is known and the integer d can be found easily from e. Thus, the security of the RSA system depends on the hardness of factoring an integer into two primes. Conversely, suppose that integer factoring is known to be an intractable problem. Does it mean that the RSA system is secure? In other words, if we have a fast algorithm breaking the RSA system, do we then have a fast factoring algorithm? The answer is yes if we make some modification on the above scheme (see Rabin (1979)). Thus, the complexity of breaking the (modified) RSA system is equivalent to the complexity of factoring the products of two primes, and the RSA system is considered secure, assuming that the function multiplication is a strong one-way function.4
4.3 Relativization
The concept of relativization originates from recursive function theory. Consider, for example, the halting problem. We may formulate it in the following form: ![]() halts
halts![]() , where Mx is the xth TM in a standard enumeration of all TMs. Now, if we consider all oracle TMs, we may ask whether the set
, where Mx is the xth TM in a standard enumeration of all TMs. Now, if we consider all oracle TMs, we may ask whether the set ![]() halts
halts![]() is recursive relative to A. This is the halting problem relative to set A. It is easily seen from the original proof for thenonrecursiveness of K that KA is nonrecursive relative to A (i.e., no oracle TM can decide KA using A as an oracle). Indeed, most results in recursive function theory can be extended to hold relative to any oracle set. We say that such results relativize. In this section, we investigate the problem of whether
is recursive relative to A. This is the halting problem relative to set A. It is easily seen from the original proof for thenonrecursiveness of K that KA is nonrecursive relative to A (i.e., no oracle TM can decide KA using A as an oracle). Indeed, most results in recursive function theory can be extended to hold relative to any oracle set. We say that such results relativize. In this section, we investigate the problem of whether ![]() in the relativized form. First, we need to define what is meant by relativizing the question of whether
in the relativized form. First, we need to define what is meant by relativizing the question of whether ![]() . For any set A, recall that PA (or P(A)) is the class of sets computable in polynomial time by oracle DTMs using A as the oracle and, similarly, NPA (or
. For any set A, recall that PA (or P(A)) is the class of sets computable in polynomial time by oracle DTMs using A as the oracle and, similarly, NPA (or ![]() ) is the class of sets accepted in polynomial time by oracle NTMs using oracle set A. Using these natural relativized forms of the complexity classes P and NP, we show that the relativized
) is the class of sets accepted in polynomial time by oracle NTMs using oracle set A. Using these natural relativized forms of the complexity classes P and NP, we show that the relativized ![]() question has both the positive and negative answers, depending on the oracle set A.
question has both the positive and negative answers, depending on the oracle set A.
Theorem 4.14
Proof
It is interesting to know that the question of whether ![]() can be answered either way relative to different oracles. What does this mean to the original unrelativized version of the question of whether P is equal to NP? Much research has been done on this subject, and yet we do not have a consensus. We summarize in the following sections some of the interesting results in this study.
can be answered either way relative to different oracles. What does this mean to the original unrelativized version of the question of whether P is equal to NP? Much research has been done on this subject, and yet we do not have a consensus. We summarize in the following sections some of the interesting results in this study.
4.4 Unrelativizable Proof Techniques
First, a common view is that the question of whether P is equal to NP is a difficult question in view of Theorem 4.14. As most proof techniques developed in recursion theory, including the basic diagonalization and simulation techniques, relativize, any attack to the ![]() question must use a new, unrelativizable proof technique. Many more contradictory relativized results like Theorem 4.14 (including some in Section 4.5) on the relations between complexity classes tend to support this viewpoint. On the other hand, some unrelativizable proof techniques do exist in complexity theory. For instance, we will apply an algebraic technique to collapse the complexity class PSPACE to a subclass IP (see Chapter 10). As there exists an oracle X that separates PSPACEX from IPX, this proof is indeedunrelativizable. Though this is a breakthrough in the theory of relativization, it seems still too early to tell whether such techniques are applicable to a wider class of questions.
question must use a new, unrelativizable proof technique. Many more contradictory relativized results like Theorem 4.14 (including some in Section 4.5) on the relations between complexity classes tend to support this viewpoint. On the other hand, some unrelativizable proof techniques do exist in complexity theory. For instance, we will apply an algebraic technique to collapse the complexity class PSPACE to a subclass IP (see Chapter 10). As there exists an oracle X that separates PSPACEX from IPX, this proof is indeedunrelativizable. Though this is a breakthrough in the theory of relativization, it seems still too early to tell whether such techniques are applicable to a wider class of questions.
4.5 Independence Results
One of the most interesting topics in set theory is the study of independence results. A statement A is said to be independent of a theory T if there exist two models M1 and M2 of T such that A is true in M1 and false in M2. If a statement A is known to be independent of the theory T, then neither A nor its negation ![]() is provable in theory T. The phenomenon of contradictory relativized results looks like a mini-independent result: neither the statement
is provable in theory T. The phenomenon of contradictory relativized results looks like a mini-independent result: neither the statement ![]() nor its negation
nor its negation ![]() is provable by relativizable techniques. This observation raises the question of whether they are provable within a formal proof system. In the following, we present a simple argument showing that this is indeed possible.
is provable by relativizable techniques. This observation raises the question of whether they are provable within a formal proof system. In the following, we present a simple argument showing that this is indeed possible.
To prepare for this result, we first briefly review the concept of a formal proof system. An axiomatizable theory is a triple ![]() , where Σ is a finite alphabet,
, where Σ is a finite alphabet, ![]() is a recursive set of well-formed formulas, and
is a recursive set of well-formed formulas, and ![]() is an r.e. set. The elements in T are called theorems. If T is recursive, we say the theory F is decidable. We are only interested in a sound theory in which we can prove the basic properties of TMs. In other words, we assume that TMs form a submodel for F, all basic properties of TMs are provable in F, and all theorems in F are true in the TM model. In the following, we let
is an r.e. set. The elements in T are called theorems. If T is recursive, we say the theory F is decidable. We are only interested in a sound theory in which we can prove the basic properties of TMs. In other words, we assume that TMs form a submodel for F, all basic properties of TMs are provable in F, and all theorems in F are true in the TM model. In the following, we let ![]() be a fixed enumeration of multi-tape DTMs.
be a fixed enumeration of multi-tape DTMs.
Theorem 4.15
Proof
We remark that although the above machine ![]() accepts an empty set, this does not imply that the statement
accepts an empty set, this does not imply that the statement ![]() is independent of F because the equivalence of
is independent of F because the equivalence of ![]() and P and the equivalence of
and P and the equivalence of ![]() and NP are not necessarily provable in the system F. So, the above result proves that for any reasonable formal proof system F, there are some statements of interests to complexity theory that are independent of F. Whether the statement
and NP are not necessarily provable in the system F. So, the above result proves that for any reasonable formal proof system F, there are some statements of interests to complexity theory that are independent of F. Whether the statement ![]() is independent of any specific formal proof system is yet still unknown.
is independent of any specific formal proof system is yet still unknown.
4.6 Positive Relativization
Still another viewpoint is that the formulation of the relativized complexity class NPA used in Theorem 4.14 does not reflect correctly the concept of nondeterministic computation. Consider the set LB in the proof of Theorem 4.14. Note that although each computation path of the oracle NTM M that accepts LB asks only one question to determine whether 0n is in B, the whole computation tree of ![]() makes an exponential number of queries. While it is recognized that this is the distinctive property of an NTM to make, in the whole computation tree, an exponential number of moves, the fact that M can access an exponential amount of information about the oracle B immediately makes the oracle NTMs much stronger than oracle DTMs. To make the relation between oracle NTMs and oracle DTMs close to that between regular NTMs and regular DTMs, we must not allow the oracle NTMs to make arbitrary queries. Instead, we would like to know whether an oracle NTM that is allowed to make, in the whole computation tree, only a polynomial number of queries is stronger than an oracle DTM. When we add these constraints to the oracle NTMs, it turns out that the relativized
makes an exponential number of queries. While it is recognized that this is the distinctive property of an NTM to make, in the whole computation tree, an exponential number of moves, the fact that M can access an exponential amount of information about the oracle B immediately makes the oracle NTMs much stronger than oracle DTMs. To make the relation between oracle NTMs and oracle DTMs close to that between regular NTMs and regular DTMs, we must not allow the oracle NTMs to make arbitrary queries. Instead, we would like to know whether an oracle NTM that is allowed to make, in the whole computation tree, only a polynomial number of queries is stronger than an oracle DTM. When we add these constraints to the oracle NTMs, it turns out that the relativized ![]() question is equivalent to the unrelativized version. This result supports the viewpoint that the relativized separation of Theorem 4.14 is due to the extra information that an oracle NTM can access, rather than the nondeterminism of the NTM and, hence, this kind of separation results bear no relation to the original unrelativized questions. This type of relativization is called positive relativization. We present a simple result of this type in the following.
question is equivalent to the unrelativized version. This result supports the viewpoint that the relativized separation of Theorem 4.14 is due to the extra information that an oracle NTM can access, rather than the nondeterminism of the NTM and, hence, this kind of separation results bear no relation to the original unrelativized questions. This type of relativization is called positive relativization. We present a simple result of this type in the following.
Definition 4.16
Theorem 4.17
Proof
The above theorem shows that we are not able to separate ![]() from PA for any oracle A unless we can show
from PA for any oracle A unless we can show ![]() . On the other hand, we note that
. On the other hand, we note that ![]() for all PSPACE-complete sets A. Thus, the relativized collapsing of
for all PSPACE-complete sets A. Thus, the relativized collapsing of ![]() to PA still works, but it only demonstrates the power of a PSPACE-complete set as an oracle and does not provide much information about the unrelativized
to PA still works, but it only demonstrates the power of a PSPACE-complete set as an oracle and does not provide much information about the unrelativized ![]() question.
question.
