Regarding an AC0 circuit of depth d as a depth-![]() circuit of the type considered in Theorem 6.37, we obtain the following.
circuit of the type considered in Theorem 6.37, we obtain the following.
Corollary 6.38
This corollary completes the proof of Theorem 6.34. Actually, we can obtain a better lower bound than that in Corollary 6.38 by using the argument in the proof of Theorem 6.37 once again. We leave it as an exercise.
The rest of this section is devoted to the proof of the Switching Lemma.
First, we notice that each AND-OR circuit corresponds to a CNF and each OR-AND circuit corresponds to a DNF. Recall, from Chapter 5, that for any Boolean function f, D(f) denotes the minimum depth of a decision tree computing f. Also recall that in a decision tree computing f, each path from root to a leaf with label 1 corresponds to an implicant. Therefore, if ![]() , then f can be computed by an OR-AND circuit of bottom fan-in at most s. The above observation shows that to prove the Switching Lemma, it suffices to prove that for any AND-OR circuit G with bottom fan-in at most t,
, then f can be computed by an OR-AND circuit of bottom fan-in at most s. The above observation shows that to prove the Switching Lemma, it suffices to prove that for any AND-OR circuit G with bottom fan-in at most t,
The following is a stronger form.
Lemma 6.39
Proof
6.7 P-Completeness
From the discussion in Section 6.4, we see that the question of whether ![]() is a major open question in complexity theory. Intuitively, this question asks whether all polynomial-time computable problems (representing problems with efficient sequential algorithms) can be recognized by circuits of poly-log depth (representing efficient parallel algorithms). Thus, it is a question of interest not only to the theoreticians who are concerned with the time/space tradeoff but also to the algorithm designers who are interested in finding efficient parallel algorithms.
is a major open question in complexity theory. Intuitively, this question asks whether all polynomial-time computable problems (representing problems with efficient sequential algorithms) can be recognized by circuits of poly-log depth (representing efficient parallel algorithms). Thus, it is a question of interest not only to the theoreticians who are concerned with the time/space tradeoff but also to the algorithm designers who are interested in finding efficient parallel algorithms.
Similar to the study of the P versus NP question, we can use the notion of P-completeness to demonstrate that some problems are the hardest problems that can be solved in polynomial time by sequential machines. If a problem A is shown to be P-complete, then it is in NC if and only if ![]() . Thus, this fact demonstrates that A is probably not in NC under the (commonly believed) assumption that
. Thus, this fact demonstrates that A is probably not in NC under the (commonly believed) assumption that ![]() .
.
Definition 6.40
Our first P-complete problem is the following:
Theorem 6.41
Proof
Some special subproblems of CVP remain P-complete. The following are two examples.
Corollary 6.42
Proof
A circuit C is a planar circuit if it can be laid out in the plane.
Corollary 6.43
Proof
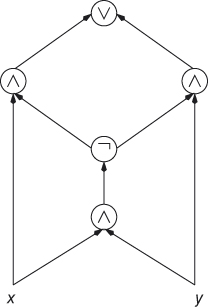
Figure 6.8 A planar circuit for  .
.
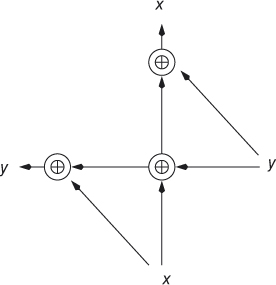
Figure 6.9 A crosser.
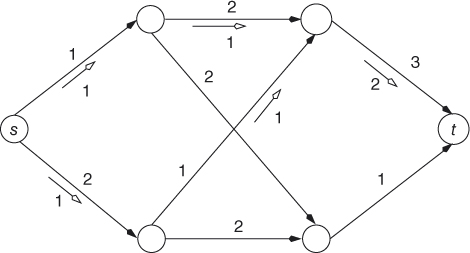
Figure 6.10 A network N and a flow f.
The next example is the odd maximum flow problem. A network ![]() is a digraph
is a digraph ![]() with two specific vertices, the source s and the sink t, and a positive-integer capacity
with two specific vertices, the source s and the sink t, and a positive-integer capacity ![]() for each edge (i,j) (see Figure 6.10). The source s has no incoming edge and the sink t has no outgoing edge. A flow in the network is an assignment of a nonnegative integer value
for each edge (i,j) (see Figure 6.10). The source s has no incoming edge and the sink t has no outgoing edge. A flow in the network is an assignment of a nonnegative integer value ![]() to each edge (i,j) such that
to each edge (i,j) such that ![]() and that for each vertex other than the source and the sink the sum of the assigned values for incoming edges equals the sum of the assigned values for outgoing edges. The value of a flow f equals the sum of the assigned values
and that for each vertex other than the source and the sink the sum of the assigned values for incoming edges equals the sum of the assigned values for outgoing edges. The value of a flow f equals the sum of the assigned values ![]() for all outgoing edges at the source s (or the sum of the assigned values
for all outgoing edges at the source s (or the sum of the assigned values ![]() for all incoming edges at the sink t).
for all incoming edges at the sink t).
Theorem 6.44
Proof
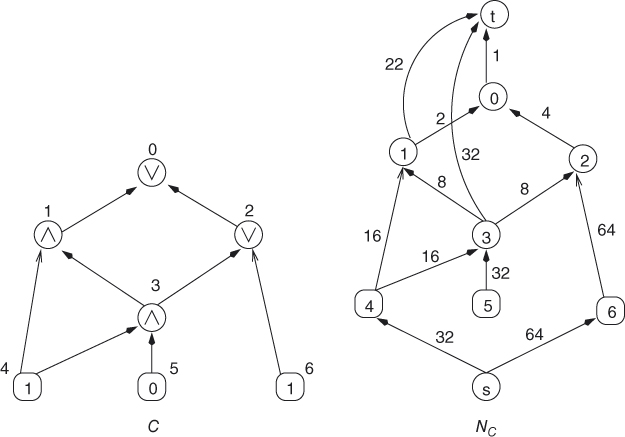
Figure 6.11 Reduction from MCV to OMF.
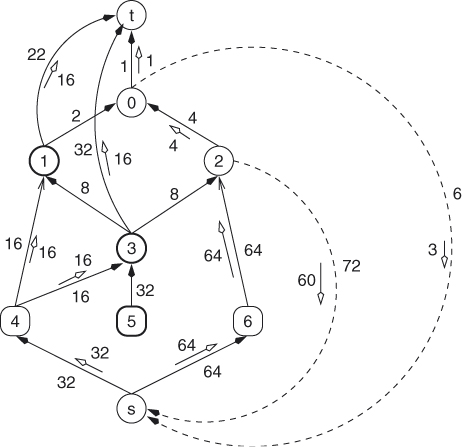
Figure 6.12 The maximum flow for NC with the imaginary edges. The dark vertices are the false ones.
We remark that there is a rich collection of P-complete problems in literature. As we mentioned before, these P-complete problems are not in NC unless ![]() . In addition to these P-complete problems, there also exist a number of problems in P for which one does not know whether it is P-complete or in NC. The following is an example.
. In addition to these P-complete problems, there also exist a number of problems in P for which one does not know whether it is P-complete or in NC. The following is an example.
A comparator gate has two output wires. In the first one, it outputs ![]() and in the second one, it outputs
and in the second one, it outputs ![]() , where x and y are its two inputs. The problem COMPARATOR CIRCUIT VALUE is the circuit value problem on circuits consisting of comparator gates. Again, it is easy to see that this problem is in P. It is, however, not known whether it is P-complete. All problems that are logarithmic-space reducible to this problem form a complexity class, called CC. It is known that
, where x and y are its two inputs. The problem COMPARATOR CIRCUIT VALUE is the circuit value problem on circuits consisting of comparator gates. Again, it is easy to see that this problem is in P. It is, however, not known whether it is P-complete. All problems that are logarithmic-space reducible to this problem form a complexity class, called CC. It is known that ![]() but not known whether the inclusions are proper or not.
but not known whether the inclusions are proper or not.
6.8 Random Circuits and RNC
A random circuit is a circuit with random variables. Let ![]() be a circuit of variables x1,
be a circuit of variables x1, ![]() , xn and y1,
, xn and y1, ![]() , ym, where y1,
, ym, where y1, ![]() , ym are random variables with the distribution satisfying
, ym are random variables with the distribution satisfying
Let a and b be two real numbers satisfying ![]() . We say a language
. We say a language ![]() is(a,b)-accepted by the random circuit
is(a,b)-accepted by the random circuit ![]() with n input variables if for all
with n input variables if for all ![]() , we have
, we have ![]() and for all
and for all ![]() , we have
, we have ![]() .
.
In the following, we show that a random circuit can be simulated by a deterministic circuit with an increase of a constant number in depth and a polynomial factor in size. Let C be a random circuit and C1, C2, ![]() , Ck be copies of C with different random variables. Define two new random circuits
, Ck be copies of C with different random variables. Define two new random circuits ![]() and
and ![]() .
.
Lemma 6.45
Proof
Theorem 6.46
Proof
The following is an application of this result to the lower bound of the parity function. We say a (deterministic) circuit C c-approximates a function f if ![]() for at least
for at least ![]() inputs x.
inputs x.
Theorem 6.47
Proof
We now define a new complexity class based on random circuits. A language is in RNC if there is a uniform family of NC circuits, with polynomially many random variables, that ![]() accepts the language. It is obvious that
accepts the language. It is obvious that ![]() . It is not known whether the inclusion is proper. Note that Theorem 6.46 showed that a language in RNC can be computed bya family of polynomial-size deterministic circuits. However, the proof was nonconstructive and so this family is a nonuniform-NC family of circuits. It is not known whether there is a way to find the deterministic circuits uniformly.
. It is not known whether the inclusion is proper. Note that Theorem 6.46 showed that a language in RNC can be computed bya family of polynomial-size deterministic circuits. However, the proof was nonconstructive and so this family is a nonuniform-NC family of circuits. It is not known whether there is a way to find the deterministic circuits uniformly.
It is known that ![]() , but it is not clear whether
, but it is not clear whether ![]() . (It is obvious that
. (It is obvious that ![]() , where R is the class of languages accepted by polynomial-time probabilistic TMs with bounded errors on inputs in the language and no error on inputs not in the language see Chapter 8). On the other hand, it is unlikely that
, where R is the class of languages accepted by polynomial-time probabilistic TMs with bounded errors on inputs in the language and no error on inputs not in the language see Chapter 8). On the other hand, it is unlikely that ![]() , and so, a problem is probably not P-hard if it is in RNC. The following is an example.
, and so, a problem is probably not P-hard if it is in RNC. The following is an example.
It is well known that PM is polynomial-time solvable (Lawler, 1976). Before we show that PM is in RNC, we first prove a probabilistic lemma, which will also be used in Chapter 9.
Lemma 6.48
Proof
Theorem 6.49
Proof
Exercises
6.1 Design a monotone Boolean circuit with at most six gates and with fan-in at most three that computes the following Boolean function:
6.2 Construct a Boolean circuit computing the function fcon on graphs of n vertices (defined in Section 5.2). How many gates do you need?
6.3 Design a multioutput circuit that combines two levels of a branching program into one.
6.4 Prove that for a monotone increasing Boolean function f,
Using this formula, find an upper bound for C(f) when f is a monotone increasing Boolean function.
6.5
- Prove that any planar circuit that computes the product of two n-bit binary integers must have at least
 vertices.
vertices. - Prove that any planar circuit that computes the product of two
 Boolean matrices must contain at least
Boolean matrices must contain at least  vertices for some constant c.
vertices for some constant c.
6.6 Show that if ![]() , then
, then ![]() .
.
6.7 Let x and y be Boolean variables, and let ![]() and
and ![]() . Show that both
. Show that both ![]() and
and ![]() can be represented monotonely from x, y, u, and v (with only AND and OR operations).
can be represented monotonely from x, y, u, and v (with only AND and OR operations).
6.8 The inverter is the collection In of functions ![]() of variables
of variables ![]() such that
such that ![]() . Design a circuit with n inputs and n outputs computing In with at most
. Design a circuit with n inputs and n outputs computing In with at most ![]() negation gates.
negation gates.
6.9
- Show that the problem of multiplying a given sequence of integers is in NC1.
- Show that the problem of multiplying a given sequence of permutations in Sn is in LOGSPACE.
6.10 Suppose that ![]() for some class
for some class ![]() that contains P as a subclass. Show that
that contains P as a subclass. Show that ![]() if and only if there exist
if and only if there exist ![]() and
and ![]() such that
such that
6.11 Prove that P/poly contains nonrecursive sets.
6.12 Prove Propositions 6.9 and 6.10.
6.13 Let log be the class of all functions h from integers to strings over {0,1} such that ![]() for some constant c > 0. Prove the following statements:
for some constant c > 0. Prove the following statements:
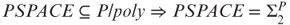 .
. .
.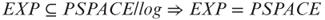 .
.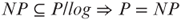 .
.
6.14 A function f is called a slice function if for some positive integer k,
- Show that a general circuit computing a slice function can be converted into a monotone circuit by adding only a polynomial number of extra gates.
- Show that it is NP-complete to determine whether a given graph G with 2n vertices has a clique of size n.
- Show that it is also NP-complete to determine whether a given graph with 2n vertices has a clique of size n or at least
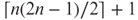 edges.
edges. - Define a sequence of slice functions that represents the above NP-complete problem.
6.15 Let G be an AND-OR circuit with bottom fan-in 1 and ρ a random restriction from Rp. Prove that the probability that ![]() cannot be switched to an OR-AND circuit with bottom fan-in less than s is bounded by qs where
cannot be switched to an OR-AND circuit with bottom fan-in less than s is bounded by qs where ![]() .
.
6.16 We refer to the proof of Lemma 6.39. Prove that there exist values ![]() for
for ![]() such that
such that
6.17 Prove that for sufficiently large n, the parity function pn cannot be computed by a depth-d circuit of size at most ![]() .
.
6.18 Let ![]() denote the maximum size of minterms of a Boolean function f. Let G be an AND-OR circuit with bottom fan-in t. Let ρ be a random restriction from Rp. Then for any Boolean formula F and s > 0, we have
denote the maximum size of minterms of a Boolean function f. Let G be an AND-OR circuit with bottom fan-in t. Let ρ be a random restriction from Rp. Then for any Boolean formula F and s > 0, we have
where q satisfies
6.19 Let ![]() be a partition of variables in a circuit. Let
be a partition of variables in a circuit. Let ![]() be a probability space of restrictions defined as follows: For each Bi, first randomly pick one value, denoted by si, from
be a probability space of restrictions defined as follows: For each Bi, first randomly pick one value, denoted by si, from ![]() with probabilities
with probabilities
Then for every ![]() , define
, define
For each ![]() , define a (deterministic) restriction
, define a (deterministic) restriction ![]() as follows: For each Bi with
as follows: For each Bi with ![]() , let Vi be the set of all variables in Bi, which are given value
, let Vi be the set of all variables in Bi, which are given value ![]() . The restriction
. The restriction ![]() selects, for each Bi, a variable yi in Vi and assigns value
selects, for each Bi, a variable yi in Vi and assigns value ![]() to yi and value 1 to all other variables in Vj. Let G be an AND-OR circuit with bottom fan-in
to yi and value 1 to all other variables in Vj. Let G be an AND-OR circuit with bottom fan-in ![]() . Then from a random restriction ρ from
. Then from a random restriction ρ from ![]() , the probability that
, the probability that ![]() is not equivalent to an OR-AND circuit with bottom fan-in
is not equivalent to an OR-AND circuit with bottom fan-in ![]() is bounded by qs where
is bounded by qs where ![]() .
.
6.20 Let ![]() be the depth-d levelable circuit that has the following structure: (a)
be the depth-d levelable circuit that has the following structure: (a) ![]() has a top OR gate, (b) the fan-in of all gates is n, (c)
has a top OR gate, (b) the fan-in of all gates is n, (c) ![]() has exactly nd variables, each variable occurring exactly once in a leaf in the positive form. Let the function computed by
has exactly nd variables, each variable occurring exactly once in a leaf in the positive form. Let the function computed by ![]() be
be ![]() . Prove that, for any k > 0, there exists an integer nk such that if a depth-d circuit D computes the function
. Prove that, for any k > 0, there exists an integer nk such that if a depth-d circuit D computes the function ![]() , with
, with ![]() , which has bottom fan-in
, which has bottom fan-in ![]() and fan-ins
and fan-ins ![]() for all gates at level 1 to d − 2 (and with fan-ins of gates at level d − 1 unrestricted), then D must have size
for all gates at level 1 to d − 2 (and with fan-ins of gates at level d − 1 unrestricted), then D must have size ![]() for some constant c > 0. [Hint: Use the random restriction of the last exercise.]
for some constant c > 0. [Hint: Use the random restriction of the last exercise.]
6.21 Let ![]() be a collection of AND-OR circuits of bottom fan-in
be a collection of AND-OR circuits of bottom fan-in ![]() . Then for a random restriction ρ from
. Then for a random restriction ρ from ![]() , the probability that every
, the probability that every ![]() can be switched to an OR-AND circuit with bottom fan-in
can be switched to an OR-AND circuit with bottom fan-in ![]() is greater than 2/3, if
is greater than 2/3, if ![]() , where
, where ![]() .
.
6.22 Show that the graph accessibility problem on undirected graphs is in LOGSPACE.
6.23 A language A is said to be NC-reducible to another language B if there exists a mapping f from strings to strings computable by a uniform family of NCi circuits for some i > 0 such that ![]() if and only if
if and only if ![]() . Prove the following:
. Prove the following:
- If A is NC-reducible to B and B is NC-reducible to C, then A is NC-reducible to C.
- If A is NC-reducible to B and B is in NC, then A is in NC.
6.24 Prove that NLOGSPACE ![]() .
.
6.25 Prove ![]() by designing and combining three logarithmic-space algorithms that perform the following tasks:
by designing and combining three logarithmic-space algorithms that perform the following tasks:
- Generate a circuit in the given uniform family of circuits with logarithmic depth.
- Transform the generated circuit to an equivalent circuit with all outdegree one (i.e., a tree-like circuit).
- Evaluate the tree-like circuit.
6.26 A Boolean circuit is called an AM2 circuit if, in the circuit, (a) on any path from an input to the output the gates are required to alternate between OR and AND gates, (b) inputs are connected to only OR gates, (c) the output also comes from an OR gate, and (d) every gate has fan-out at most two. The problem AM2 CIRCUIT VALUE is defined as follows: Given an AM2 circuit and an assignment to its variables, determine whether the circuit value equals 1. Prove that AM2 CIRCUIT VALUE is P-complete.
6.27 An NAND gate can be obtained by putting a NOT gate at output of an AND gate. An NAND circuit is a Boolean circuit consisting of only NAND gates. The NAND CIRCUIT VALUE problem is to determine, for a given NAND circuit and a given assignment to its variables, whether the circuit value equals 1. Prove that NAND CIRCUIT VALUE is P-complete.
6.28 Show that the following problem is P-complete: Given a network ![]() and a nonnegative integer k, determine whether the maximum flow of N has value
and a nonnegative integer k, determine whether the maximum flow of N has value ![]() .
.
6.29 Prove than if a bipartite graph has a perfect matching, then a perfect matching can be found in RNC.
6.30 Show that if ![]() , then
, then ![]() .
.
6.31 An r-circuit is a circuit with AND and OR gates of fan-in two and at most r negation gates. Let ![]() denote the size of the smallest r-circuit computing f. Show that for any Boolean function f of n variables,
denote the size of the smallest r-circuit computing f. Show that for any Boolean function f of n variables,
6.32 Prove that if a random circuit ![]() accepts A, then
accepts A, then ![]() accepts A.
accepts A.
6.33 Show that if ![]() , then
, then ![]() , where pn is the parity function of n variables.
, where pn is the parity function of n variables.
6.34 Show that the problem of finding the determinant of an integer matrix is in NC2.
Historical Notes
Shannon (1949) first considered the circuit size of a Boolean function as a measure of its computational complexity. Lupanov (1958) showed the general upper bound ![]() . Fischer (1974) proved the existence of Boolean functions with circuit complexity
. Fischer (1974) proved the existence of Boolean functions with circuit complexity ![]() . An explicit language with circuit complexity
. An explicit language with circuit complexity ![]() was found by Blum (1984). See Dunne (1988) and Wegener (1987) for more complete treatment on Boolean circuits. Karp and Lipton (1982) studied the class of sets having polynomial-size circuits and obtained a number of results on P/poly, including Theorem 6.11 and Exercise 6.13. Sparse sets are first studied in Lynch (1975) and Berman and Hartmanis (1977). They are further studied in Chapter 7. For the sets with succinct descriptions (such as sets with polynomial-size circuits), see the survey paper of Balcázar et al. (1997).
was found by Blum (1984). See Dunne (1988) and Wegener (1987) for more complete treatment on Boolean circuits. Karp and Lipton (1982) studied the class of sets having polynomial-size circuits and obtained a number of results on P/poly, including Theorem 6.11 and Exercise 6.13. Sparse sets are first studied in Lynch (1975) and Berman and Hartmanis (1977). They are further studied in Chapter 7. For the sets with succinct descriptions (such as sets with polynomial-size circuits), see the survey paper of Balcázar et al. (1997).
Razborov (1985a) obtained the first superpolynomial lower bound ![]() for the size of monotone circuits computing the function
for the size of monotone circuits computing the function ![]() . The exponential lower bound of Theorem 6.15 was given by Alon and Boppana (1987). Razborov (1985b) showed that the perfect matching problem for bipartite graphs also requires monotone circuits of superpolynomial size. Tardos (1988) showed an exponential lower bound for another problem in P. Berkowitz (1982) introduced slice functions and showed that circuits computing slice functions can be converted into monotone circuits with a polynomial number of additional gates (see Exercise 6.14). He also pointed out that there exist NP-complete slice functions. Yao (1994) adapted Razborov's technique to show that the connectivity requires depth
. The exponential lower bound of Theorem 6.15 was given by Alon and Boppana (1987). Razborov (1985b) showed that the perfect matching problem for bipartite graphs also requires monotone circuits of superpolynomial size. Tardos (1988) showed an exponential lower bound for another problem in P. Berkowitz (1982) introduced slice functions and showed that circuits computing slice functions can be converted into monotone circuits with a polynomial number of additional gates (see Exercise 6.14). He also pointed out that there exist NP-complete slice functions. Yao (1994) adapted Razborov's technique to show that the connectivity requires depth ![]() in a monotone circuit. Goldman and Hastad (1995) improved the bound to
in a monotone circuit. Goldman and Hastad (1995) improved the bound to ![]() . There are also many references on circuits with limited number of negation gates; see, for instance, Beals et al. (1995).
. There are also many references on circuits with limited number of negation gates; see, for instance, Beals et al. (1995).
The class NC was first defined by Nick Pippenger (1979); indeed, the term NC was coined by Cook to mean “Nick's Class.” There are, in literature, a number of models for parallel computation, including PRAMs (Fortune and Wyllie, 1978), SIMDAGs (Goldschlager, 1978),Alternating Turing machines (Chandra et al., 1981), and vector machines (Pratt et al., 1974). See, for instance, van Emde Boas (1990) for a survey of these models and their relations to the Boolean circuit model. The fact that LOGSPACE and NLOGSPACE are in NC2 was proved by Borodin (1977). Exercise 6.9 is from Beame et al. (1984), Cook and McKenzie (1987), and Immerman and Landau (1989). Exercise 6.22 is from Reingold (2008).
The fact that the parity function is not in AC0 was first proved by Furst et al. (1984) and Ajtai (1983). They proved that the parity function requires constant-depth circuits of superpolynomial size. Yao (1985) pushed up this lower bound to exponential size. Hastad (1986a, 1986b) simplified Yao's proof and proved the first Switching Lemma. Exercises 6.18 and 6.19 are from Hastad (1986a, 1986b). The idea of using the inversion formula in the proof of the Switching Lemma was initially proposed by Moran (1987). However, in his proof, he used ![]() instead of D(G), so that the inequality corresponding to (6.7) was incorrect. The current idea of using D(G) was suggested by Cai (1991). For other applications of the random restriction and the Switching Lemma, see, for instance, Aiello et al. (1990) and Ko (1989b). Exercise 6.21 is from Ko (1989a). Smolensky (1987) extended Yao's result to modulo functions. Fortnow and Laplante (1995) (see also section 6.12 of Li and Vitanyi (1997)) offer a different proof of Hastad's Lemma using the notion of Kolmogorov complexity.
instead of D(G), so that the inequality corresponding to (6.7) was incorrect. The current idea of using D(G) was suggested by Cai (1991). For other applications of the random restriction and the Switching Lemma, see, for instance, Aiello et al. (1990) and Ko (1989b). Exercise 6.21 is from Ko (1989a). Smolensky (1987) extended Yao's result to modulo functions. Fortnow and Laplante (1995) (see also section 6.12 of Li and Vitanyi (1997)) offer a different proof of Hastad's Lemma using the notion of Kolmogorov complexity.
P-complete problems were first studied by Cook (1973b). The P-completeness of the the problem CVP was established by Ladner (1975b). The circuit value problem for monotone and planar circuits was studied by Goldschlager (1977). Exercise 6.5 is from Lipton and Tarjan (1980). The problem OMF is proved to be P-complete by Goldschlager et al. (1982). Greenlaw et al. (1995) included a list of hundreds of P-complete problems. Mayr and Subramanian (1989) defined the class CC and studied its properties.
Random circuits were studied by Ajtai and Ben-Or (1984). Feather (1984) showed that finding the size of the maximum matching is in RNC. Karp et al. (1986) found the first RNC algorithm for finding the maximum matching. Our proof using the Isolation Lemma is from Mulmuley et al. (1987). The fact that the determinant of an integer matrix can be computed in NC was first proved by Csansky (1976) and Borodin, Cook and Pippenger (1983). See Cook (1985) for more discussions about the problem of computing integer determinants.
