Using the notion of polynomial-time Turing reducibility, it is not hard to show that the search problem of TSP that asks for the minimum-cost tour is equivalent to the above decision problem (see Exercise 2.18). Therefore, the search problem of TSP is also NP-hard. In the following, we show that the approximation to TSP is also NP-hard. For each graph G with a cost function c on its edges, let An important subproblem of TSP is the traveling salesman problem satisfying the triangle inequality, that is, the problem whose cost function c satisfies for any three vertices Note that the graph G′ and its cost function c constructed in the reduction from HC to TSP of Theorem 2.25 do not satisfy the triangle inequality. Yet, it is easy to modify that proof to show that TSP with the triangle inequality restriction on the cost function is still NP-complete (see Exercise 2.17). On the other hand, the story is quite different when we consider the approximation to this restricted version of TSP. Namely, there exists a polynomial-time algorithm that solves the problem r-APPROX-TSP, for all To establish this result, we first review three well-known problems that all are known to have polynomial-time solutions. Let Let A graph Now we are ready for the following result: Figure 2.3 (a) An Eulerian circuit; (b) a shortcut. In the above, we have considered three variations of the problem TSP, namely, TSP on arbitrary graphs, TSP on graphs that satisfy the triangle inequality, and TSP on graphs on the Euclidean plane. We have seen that the optimization versions of these three variations of TSP are all NP-complete, but their approximation versions belong to three different complexity classes. Let us review these three complexity classes of approximation problems. The first class consists of approximation problems that are NP-hard for all approximation ratios r > 1. The problem APPROX-TSP on arbitrary graphs belongs to this class. The second class consists of approximation problems for each of which there exists a constant r0 such that the problem is NP-hard for all approximation ratios The third class consists of all approximation problems that are polynomial-time solvable for all ratios r > 1. Problems in the third class can be further classified into two subclasses. A problem may have, for each k ≥ 1, a polynomial-time algorithm Ak for the approximation ratio Intuitively, we say each ci is the cost of item i and vi is the value of item i, and the problem KS is to maximize the total value while keeping the total cost below a given bound B. The approximation version of the optimization problem KNAPSACK, called APPROX-KS, is to find, for a given list L, a given integer B, and a given rational r > 1, an index set Theorem 2.25
Proof
![]() denote the cost of a minimum-cost tour of G. We formulate the problem of approximation to TSP as the following search problem. Let r be a rational number with r ≥ 1.
denote the cost of a minimum-cost tour of G. We formulate the problem of approximation to TSP as the following search problem. Let r be a rational number with r ≥ 1.r-APPROX-TSP: Given a complete graph
![]() with a cost function
with a cost function ![]() , find a tour of G with the total cost
, find a tour of G with the total cost ![]() .
.Theorem 2.26
Proof
![]()
![]() of the graph G. For instance, if the input graph G is a Euclidean graph in the sense that its vertices are points in an Euclidean space Ek and the cost of an edge is the distance of the two end points in this space, then this cost function satisfies the triangle inequality.
of the graph G. For instance, if the input graph G is a Euclidean graph in the sense that its vertices are points in an Euclidean space Ek and the cost of an edge is the distance of the two end points in this space, then this cost function satisfies the triangle inequality.![]() , on graphs having the triangle inequality. It is an open question whether this bound
, on graphs having the triangle inequality. It is an open question whether this bound ![]() can be improved. Furthermore, if the graph G is a Euclidean graph on the two-dimensional plane E2, then there exist polynomial-time algorithm that solves the problem r-APPROX-TSP, for all r > 1. In the following, we present a polynomial-time approximation algorithm for
can be improved. Furthermore, if the graph G is a Euclidean graph on the two-dimensional plane E2, then there exist polynomial-time algorithm that solves the problem r-APPROX-TSP, for all r > 1. In the following, we present a polynomial-time approximation algorithm for ![]() -APPROX-TSP on graphs satisfying the triangle inequality. We leave the problem r-APPROX-TSP for graphs on the Euclidean plane as an exercise (Exercise 2.19).
-APPROX-TSP on graphs satisfying the triangle inequality. We leave the problem r-APPROX-TSP for graphs on the Euclidean plane as an exercise (Exercise 2.19).![]() be a connected graph. A spanning tree of the graph G is a subgraph
be a connected graph. A spanning tree of the graph G is a subgraph ![]() with the same vertex set V such that T is a tree, that is, T is connected and contains no cycle. For a graph G with a cost function c on edges, the minimum spanning tree problem is to find a spanning tree T of G with the minimum total cost. The existence of a polynomial-time algorithm for the minimum spanning tree problem is well known (see, e.g., Aho, Hopcroft and Ullman (1974)).
with the same vertex set V such that T is a tree, that is, T is connected and contains no cycle. For a graph G with a cost function c on edges, the minimum spanning tree problem is to find a spanning tree T of G with the minimum total cost. The existence of a polynomial-time algorithm for the minimum spanning tree problem is well known (see, e.g., Aho, Hopcroft and Ullman (1974)).![]() be a complete graph of an even number of vertices and c a cost function on the edges. A matching of the graph G is a partition of the set V into
be a complete graph of an even number of vertices and c a cost function on the edges. A matching of the graph G is a partition of the set V into ![]() subsets each of two vertices. The cost of a matching is the total cost of the edges connecting the vertices in the same subsets of the matching. The minimum matching problem is to find a minimum-cost matching of a given graph G with a cost function c. The minimum matching problem is polynomial-time solvable (Lawler, 1976).
subsets each of two vertices. The cost of a matching is the total cost of the edges connecting the vertices in the same subsets of the matching. The minimum matching problem is to find a minimum-cost matching of a given graph G with a cost function c. The minimum matching problem is polynomial-time solvable (Lawler, 1976).![]() is an Eulerian graph if each vertex
is an Eulerian graph if each vertex ![]() has a positive, even degree. An Eulerian circuit of a graph
has a positive, even degree. An Eulerian circuit of a graph ![]() is a path that passes through each edge
is a path that passes through each edge ![]() exactly once. The Eulerian circuit problem is to find anEulerian circuit for a given graph. This problem, although similar to the problem HC, has a simple solution in polynomial time. That is, a graph has an Eulerian circuit if and only if it is an Eulerian graph. In addition, there is a polynomial-time algorithm finding an Eulerian tour of any given Eulerian graph (Liu, 1968).
exactly once. The Eulerian circuit problem is to find anEulerian circuit for a given graph. This problem, although similar to the problem HC, has a simple solution in polynomial time. That is, a graph has an Eulerian circuit if and only if it is an Eulerian graph. In addition, there is a polynomial-time algorithm finding an Eulerian tour of any given Eulerian graph (Liu, 1968).Theorem 2.27
Proof
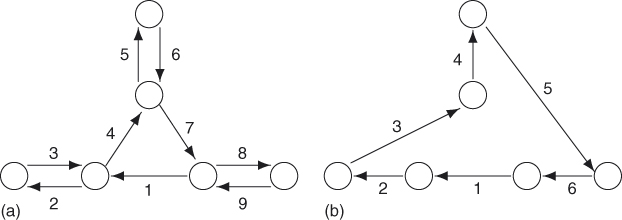
![]() and is polynomial-time solvable for
and is polynomial-time solvable for ![]() . The problem APPROX-TSP on graphs satisfying the triangle inequality is a candidate of problems in the second class. We will see in Chapter 11 more approximation problems that belong to the first and second classes.
. The problem APPROX-TSP on graphs satisfying the triangle inequality is a candidate of problems in the second class. We will see in Chapter 11 more approximation problems that belong to the first and second classes.![]() , such that the runtime of the algorithm Ak is polynomial in the input size but superpolynomial in the parameter k. We say such a problem has a polynomial-time approximation scheme (PTAS). The problem APPROX-TSP on graphs on the Euclidean plane belongs to this subclass. A problem with a PTAS, although considered as polynomial-time approximable, is not feasibly solvable when we need good approximation with a small ratio r ≈ 1. Instead, we would like to have a fully polynomial-time approximation Scheme (FPTAS) A that takes a problem instance and an approximation parameter k as inputs and outputs an approximate solution with the approximation ratio
, such that the runtime of the algorithm Ak is polynomial in the input size but superpolynomial in the parameter k. We say such a problem has a polynomial-time approximation scheme (PTAS). The problem APPROX-TSP on graphs on the Euclidean plane belongs to this subclass. A problem with a PTAS, although considered as polynomial-time approximable, is not feasibly solvable when we need good approximation with a small ratio r ≈ 1. Instead, we would like to have a fully polynomial-time approximation Scheme (FPTAS) A that takes a problem instance and an approximation parameter k as inputs and outputs an approximate solution with the approximation ratio ![]() in time polynomial in the instance size and the parameter k. Such a scheme would be the best we can expect, short of proving
in time polynomial in the instance size and the parameter k. Such a scheme would be the best we can expect, short of proving ![]() . In the following, we demonstrate that the approximation version of the knapsack problem has an FPTAS.
. In the following, we demonstrate that the approximation version of the knapsack problem has an FPTAS.KNAPSACK (KS): Given a list of positive integer pairs
![]() ,
, ![]() and an integer
and an integer ![]() , find the set
, find the set ![]() that maximizes
that maximizes ![]() , subject to the condition of
, subject to the condition of ![]() .
.![]() , such that
, such that ![]() and
and ![]() , where
, where ![]() is the maximum solution VI with respect to input (L,B). It is clear that the sum of subset problem SS is a subproblem of KS and, hence, KS is NP-hard.
is the maximum solution VI with respect to input (L,B). It is clear that the sum of subset problem SS is a subproblem of KS and, hence, KS is NP-hard.
Theorem 2.28
Proof
Remark
Exercises
2.1 A binary relation ![]() is called polynomially honest if there exists a polynomial function p such that
is called polynomially honest if there exists a polynomial function p such that ![]() only if
only if ![]() and
and ![]() . A function
. A function ![]() is polynomially honest if the relation
is polynomially honest if the relation ![]() is polynomially honest. Prove that
is polynomially honest. Prove that ![]() is in NP if and only if
is in NP if and only if ![]() for some polynomially honest function
for some polynomially honest function ![]() .
.
2.2 For any set B, define ![]() . Assume that
. Assume that ![]() such that for each x,
such that for each x, ![]() for some polynomially honest relation
for some polynomially honest relation ![]() . Prove that
. Prove that ![]() and
and ![]() . Under what conditions does the relation
. Under what conditions does the relation ![]() hold?
hold?
- a. Prove that if
 , then
, then  .
. - Prove that if
 , then
, then  .
.
2.4 Assume that A is NP-complete and ![]() . Prove that if
. Prove that if ![]() , then
, then ![]() is NP-complete. What can you say about the complexity of
is NP-complete. What can you say about the complexity of ![]() if A and B are not known to be disjoint?
if A and B are not known to be disjoint?
2.5 Prove that a nonempty finite set is NP-complete if and only if ![]() .
.
2.6 Assume that set A has the following property: There exist a set ![]() and two polynomial functions p,q, such that for any string
and two polynomial functions p,q, such that for any string ![]() ,
, ![]() if and only if there are at least
if and only if there are at least ![]() strings y of length
strings y of length ![]() satisfying
satisfying ![]() . Prove that
. Prove that ![]() .
.
2.7 Let Fx be the Boolean formula constructed from an input x of length 2n in the proof of Cook's theorem and ![]() be the 3-CNF formula obtained from Fx by the reduction of Corollary 2.13. Show that the clauses of the formula
be the 3-CNF formula obtained from Fx by the reduction of Corollary 2.13. Show that the clauses of the formula ![]() can be labeled as
can be labeled as ![]() so that the function
so that the function ![]() is computable in time polynomial in n.
is computable in time polynomial in n.
2.8 Prove that a DNF formula can be switched in polynomial time to a CNF formula, with possibly more variables, preserving satisfiability.
2.9 Prove that if ![]() , then there is no polynomial-time algorithm that switches a CNF formula to a DNF formula preserving satisfiability.
, then there is no polynomial-time algorithm that switches a CNF formula to a DNF formula preserving satisfiability.
2.10 Define 2-SAT to be the problem of determining whether a given 2-CNF formula, which is a CNF formula with each clause having at most two literals, is satisfiable. Prove that 2-SAT is in P.
2.11 For each of the following problems, prove that it is NP-complete.
- 1-IN-3-3SAT: Given a 3-CNF formula, determine whether there is a Boolean assignment that assigns the value TRUE to exactly one literal of each clause.
- NOT-ALL-EQUAL-3SAT: Given a 3-CNF formula, determine whether there is a Boolean assignment that assigns the value TRUE to at least one and at most two literals of each clause.
- 3-DIMENSIONAL MATCHING (3DM): Given three disjoint sets A,B, and C; each of n elements; and a set
 , determine whether there is a subset
, determine whether there is a subset  of size n such that no two elements of T agree in any of three coordinates.
of size n such that no two elements of T agree in any of three coordinates. - SUBGRAPH ISOMORPHISM: Given two graphs G and H, determine whether G has a subgraph that is isomorphic to graph H.
- SET SPLITTING: Given a finite set S and a collection C of subsets of S, determine whether there is a partition of S into two subsets S1 and S2, such that no subset T in C is contained in either S1 or S2.
2.12 Formally define the notion of the computation of a function-oracle DTM and the notion of a function-oracle DTM computing a partial function g relative to a total function f.
2.13 Prove that if A is computable by an oracle TM M using oracle B, such that ![]() is bounded by a polynomial function p, then
is bounded by a polynomial function p, then ![]() . (That is,
. (That is, ![]() via some other oracle machine M1 that halts in polynomial time for all oracles.)
via some other oracle machine M1 that halts in polynomial time for all oracles.)
2.14 The polynomial-time Turing reducibility is often called an adaptive reducibility because the ![]() th query made by an oracle machine M on an input x may depend on the answers to the first k queries. A nonadaptive version of the polynomial-time Turing reducibility works as follows: The oracle machine must determine all the queries it wants to ask before the first query is made, and then it presents all queries to the oracle together. Such a reducibility is called a polynomial-time truth-table reducibility and denoted by
th query made by an oracle machine M on an input x may depend on the answers to the first k queries. A nonadaptive version of the polynomial-time Turing reducibility works as follows: The oracle machine must determine all the queries it wants to ask before the first query is made, and then it presents all queries to the oracle together. Such a reducibility is called a polynomial-time truth-table reducibility and denoted by ![]() . Formally, we define
. Formally, we define ![]() if there exists a function
if there exists a function ![]() and a set
and a set ![]() such that for any x,
such that for any x, ![]() if and only if
if and only if ![]() , where
, where ![]() and χB is the characteristic function of set B.
and χB is the characteristic function of set B.
- Prove that
 .
. - Prove that there exist sets A,B, such that
 but
but  .
. - Prove that there exist sets C,D, such that
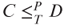 but
but 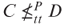 .
.
2.15 An oracle TM M is called a positive oracle machine if for all oracles X, Y, ![]() implies
implies ![]() . We say that A is polynomial-time positive Turing reducible to B, denoted by
. We say that A is polynomial-time positive Turing reducible to B, denoted by ![]() , if
, if ![]() via a positive oracle machine M.
via a positive oracle machine M.
- Prove that NP is closed under the
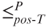 -reducibility, that is,
-reducibility, that is, 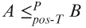 and
and 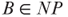 imply
imply  .
. - Show that there exist sets A,B, such that
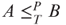 but
but 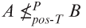 .
.
2.16
- a. Using the first type of space measure for oracle TMs (i.e., the space measure that includes the space in the query tape), show that there exists a set A that is not log-space Turing reducible to itself.
- Using the second type of space measure for oracle TMs (i.e., the space measure that excludes the query tape while requiring the query tape to be write only), show that there exist sets A,B, such that
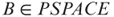 ,
, 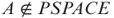 , but A is computable by a polynomial-space-bounded oracle machine with respect to the oracle B, that is, PSPACE is not closed under the polynomial-space Turing reducibility.
, but A is computable by a polynomial-space-bounded oracle machine with respect to the oracle B, that is, PSPACE is not closed under the polynomial-space Turing reducibility. - Using the second type of space measure for oracle TMs, show that the polynomial-space Turing reducibility does not satisfy the transitivity property (and, hence, should not be called a reducibility).
2.17 Prove that the problem TSP on graphs that satisfy the triangle inequality is still NP-complete.
2.18 In this exercise, we consider the decision problem EXACT-TSP that asks, for a given weighted graph G and an integer K, whether the cost of a minimum-cost tour of G is exactly K and the search problem MIN-TSP that asks for a minimum-cost tour of a given weighted graph G.
- Show that EXACT-TSP is
 -equivalent to TSP.
-equivalent to TSP. - Show that MIN-TSP is
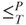 -equivalent to TSP.
-equivalent to TSP. - The notion of polynomial-time many-one reducibility can be extended to functions. Namely, we say function ϕ is polynomial-time many-one reducible to function ψ if there exist two polynomial-time computable functions f and g such that for each x,
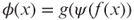 . Let MAX-3SAT be the problem that asks, for a given 3-CNF formula and a given weight function on clauses, to find the Boolean assignment that maximizes the weight of satisfied clauses. Show that MAX-3SAT is
. Let MAX-3SAT be the problem that asks, for a given 3-CNF formula and a given weight function on clauses, to find the Boolean assignment that maximizes the weight of satisfied clauses. Show that MAX-3SAT is 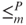 -complete for the class
-complete for the class  .
. - Prove that MIN-TSP is
 -complete for the class
-complete for the class 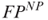 by reducing MAX-3SAT to MIN-TSP.
by reducing MAX-3SAT to MIN-TSP.
2.19 Prove that r-APPROX-TSP is polynomial-time solvable for all r > 1 when it is restricted to graphs on the two-dimensional Euclidean plane.
2.20 For each of the following optimization problems, first define a decision version of the problem, then prove that the search version is ![]() -equivalent to the decision version and that the decision version is NP-complete.
-equivalent to the decision version and that the decision version is NP-complete.
- GRAPH COLORING (GCOLOR): Given a graph
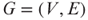 , find a (coloring) function
, find a (coloring) function  that uses the minimum number k of colors such that
that uses the minimum number k of colors such that 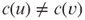 for any two adjacent vertices
for any two adjacent vertices 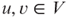 .
. - BIN PACKING (BP): Given a list of rational numbers
 , with
, with  , for each
, for each 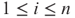 , find a partition L into k parts
, find a partition L into k parts 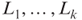 such that the sum of each part Li,
such that the sum of each part Li, 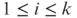 , is at most 1 and the number k of parts is minimized.
, is at most 1 and the number k of parts is minimized. - SHORTEST COMMON SUPERSTRING (SCS): Given a list of strings
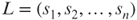 over a finite alphabet Σ, find the shortest string t such that each si is a substring of t.
over a finite alphabet Σ, find the shortest string t such that each si is a substring of t.
- a. Prove that
 -APPROX-GCOLOR is NP-hard.
-APPROX-GCOLOR is NP-hard. - Prove that APPROX-BP has a PTAS.
- Prove that 3-APPROX-SCS is solvable in polynomial time.
2.22 In this problem, we explore the similarity between the computation of an NTM and the computation of an oracle DTM. Assume that M1 is an NTM in which each nondeterministic move has exactly two choices. Then, we can construct an oracle DTM M2 to simulate M1 as follows: On any input x, ![]() simulates
simulates ![]() deterministically; when M1 makes a nondeterministic move, M2 asks the oracle H whether y is in H, where y is a string encoding the computation of
deterministically; when M1 makes a nondeterministic move, M2 asks the oracle H whether y is in H, where y is a string encoding the computation of ![]() up to this point. It follows the first choice if and only if the answer to the query is YES.
up to this point. It follows the first choice if and only if the answer to the query is YES.
- Assume that M1 is a polynomial-time NTM. Prove that there exists an oracle
 such that foreach x,
such that foreach x, 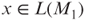 if and only if
if and only if 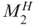 accepts x in polynomial time.
accepts x in polynomial time. - We say M2 is a robust oracle machine if for any oracle H,
 , that is, the set of strings accepted by M2 does not depend on the oracle. Show that a set A is computable by a robust oracle machine M with the property that relative to some oracle H,
, that is, the set of strings accepted by M2 does not depend on the oracle. Show that a set A is computable by a robust oracle machine M with the property that relative to some oracle H, 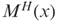 always halts in polynomial time, if and only if
always halts in polynomial time, if and only if 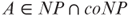 .
.
2.23 Determine the complexity of the following problem: Given a set of points on the first quadrant of the rectilinear plane (the plane with the rectilinear metric: ![]() ), find a minimum total-edge-length-directed tree rooted at the origin that connect the given points with edges in direction either to the right or upward.
), find a minimum total-edge-length-directed tree rooted at the origin that connect the given points with edges in direction either to the right or upward.
When I feel like exercising,I just lie down until the feeling goes away.
—Robert M. Hutchins
Historical Notes
Many-one and Turing reducibilities are major tools in recursion theory. Rogers (1967) contains a complete treatment of these topics. The first natural NP-complete problem, SAT, was proved by Cook (1971), who used the polynomial-time Turing reducibility. Karp (1972) proved more natural NP-complete problems, including the problems VC, CLIQUE, IS, HC, IP, SS, PARTITION, KS, 3DM, and GCOLOR, under the polynomial-time many-one reducibility. Levin (1973) independently proved the NP-completeness of the tiling problem. Garey and Johnson (1979) collected several hundred NP-complete problems. They also included a discussion on the proof techniques to establish NP-completeness results. The problem TSP has been studied widely in literature. The approximation algorithm for TSP satisfying the triangle inequality is from Christofides (1976). The PTAS for TSP on two-dimensional Euclidean plane (Exercise 2.19) is from Arora (1996). The FPTAS for KS is from Ibarra and Kim (1975). Fora complete treatment of approximation algorithms, see Du, Ko, and Hu (2012).
The fact that 2-SAT is polynomial-time solvable was proved in Cook (1971). A number of variations of 3-SAT, including 1-IN-3-SAT and NOT-ALL-EQUAL-3SAT, are shown to be NP-complete in Schaefer (1978a). The problem SET SPLITTING was proved to be NP-complete by Lovasz (1973). Different notions of polynomial-time reducibilities have been compared in Ladner et al. (1975). Exercise 2.14 is taken from Ladner et al. (1975). The two models of space-bounded oracle machines discussed in Section 2.4 and other modifications have been studied by Ladner and Lynch (1976), Orponen (1983), Ruzzo et al. (1984), Buss (1986), and Wilson (1988). The nonapproximability results on GCOLOR can be found in Garey and Johnson (1976), Lund and Yannakakis (1994), and Khanna et al. (1993). Karmarkar and Karp (1982) gave a PTAS for BIN PACKING. See also Coffman et al. (1985) for a survey on BIN PACKING. The problem SHORTEST COMMON SUPERSTRING was first proved to be NP-complete by Maier and Storer (1977). The ratio-3 approximation algorithm was given by Blum et al. (1991), who also showed, by the results of Chapter 11, that r-APPROX-SCS is NP-hard for some r > 1. Exercise 2.22 is from Schöning (1985) and Ko (1987).
