Chapter 10
Interactive Proof Systems
Those who consider a thing proved simply
because it is in print are fools.
—Maimonides
The complexity classes RP and BPP are the probabilistic extensions of the deterministic feasible class P. In this chapter, we study interactive proof systems as the probabilistic extension of the polynomial-time hierarchy and the class PSPACE. Although the original motivation of interactive proof systems is for their applications in the theory of cryptography, they have found many interesting applications in complexity theory too. In particular, we will discuss characterizations of complexity classes between NP and PSPACE in terms of interactive proof systems. We also demonstrate an interesting application of this study in which some intractable problems in NP are proved to be not NP- complete unless the polynomial-time hierarchy collapses.
10.1 Examples and Definitions
The notion of interactive proof systems is most easily explained from a game-theoretic view of the complexity classes. In the general setting, each problem A is interpreted as a two-person game in which the first player, the prover, tries to convince the second player, the verifier, that a given instance x is in A. On a given instance x, each player takes turn sending a string yi to the other player, where the ith string yi may depend on the input x and the previous strings y1, ![]() ,
, ![]() . After a number m of moves, the prover wins the game if the verifier is able to verify that the strings x, y1,
. After a number m of moves, the prover wins the game if the verifier is able to verify that the strings x, y1, ![]() , ym satisfy a predetermined condition; otherwise, the verifier wins. Depending on the computational power of the two players, and on the type of protocols allowed between the two players, this game-theoretic view of the computational problems can be used to characterize some familiar complexity classes.
, ym satisfy a predetermined condition; otherwise, the verifier wins. Depending on the computational power of the two players, and on the type of protocols allowed between the two players, this game-theoretic view of the computational problems can be used to characterize some familiar complexity classes.
As a simple example, consider the famous NP-complete problem SAT. To prove that a Boolean formula F is satisfiable, the prover simply sends a truth assignment t on the variables that occurred in F to the verifier, then the verifier verifies, in polynomial time, whether t satisfies F or not and accepts F if t indeed satisfies F. Thus, we say that SAT has a proof system with the following properties:
- The verifier has the power of a polynomial-time DTM, and the prover has the unlimited computational power.
- The game lasts for one round only, with the prover making the first move.
- A formula F is in SAT if and only if the prover is able to win the game on F.
Indeed, it is easy to see that the class NP consists of exactly those sets having proof systems of the above properties.
A more interesting example is the proof systems for the polynomial-time hierarchy. Recall the following alternating quantifier characterization of the polynomial-time hierarchy (Theorem 3.8): A set A is in ![]() if and only if there exist a polynomial-time computable predicate R and a polynomial q such that for all x,
if and only if there exist a polynomial-time computable predicate R and a polynomial q such that for all x,
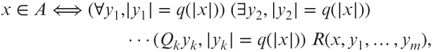
where ![]() if k is odd and
if k is odd and ![]() if k is even. From the game-theoretic point of view, the above characterization means that a set A in
if k is even. From the game-theoretic point of view, the above characterization means that a set A in ![]() has a proof system of the following properties:
has a proof system of the following properties:
- The verifier has the power of a polynomial-time DTM, and the prover has the unlimited computational power.
- The game lasts for exactly k rounds, with the verifier making the first move.
- An instance x is in A if and only if the prover has a winning strategy on x.
The above game-theoretic view of the complexity classes in PH, though helpful in our understanding of the problems in these classes, does not help us to prove them efficiently in practice. For instance, consider the above game for some set ![]() . This game consists of only two moves: the verifier sends to the prover a string y1 and the prover responds with a string y2. Following these two moves, the verifier verifies whether
. This game consists of only two moves: the verifier sends to the prover a string y1 and the prover responds with a string y2. Following these two moves, the verifier verifies whether ![]() holds and decides who wins the game. In this game, even if the prover is able to win the games on the same input x polynomially many times (with respect to different strings y1), the verifier is not necessarily convinced that the prover has a winning strategy. The reason is that the verifier has an exponential number of choices for the first string y1 and only polynomially many of them have been defeated by the prover. The prover might simply be lucky in winning in these special cases. An exhaustive proof by the prover would convince the verifier that x indeed belongs to A but it would, unfortunately, take an exponential amount of time.
holds and decides who wins the game. In this game, even if the prover is able to win the games on the same input x polynomially many times (with respect to different strings y1), the verifier is not necessarily convinced that the prover has a winning strategy. The reason is that the verifier has an exponential number of choices for the first string y1 and only polynomially many of them have been defeated by the prover. The prover might simply be lucky in winning in these special cases. An exhaustive proof by the prover would convince the verifier that x indeed belongs to A but it would, unfortunately, take an exponential amount of time.
Following the spirit of probabilistic computing, we studied in Chapter 8, it is possible, however, that for a subclass of problems A in ![]() , the prover is able to demonstrate probabilistically that astring x is in A in polynomial time. To do this, the prover first shows the verifier that if
, the prover is able to demonstrate probabilistically that astring x is in A in polynomial time. To do this, the prover first shows the verifier that if ![]() , then there exist not just one but many bad strings y1 such that
, then there exist not just one but many bad strings y1 such that ![]()
![]() . (Therefore, only a subclass of problems A in
. (Therefore, only a subclass of problems A in ![]() qualify.) Assume, for instance, there are
qualify.) Assume, for instance, there are ![]() such bad y1's for some constant c > 0. Then, the verifier may randomly choose a string z1 of length
such bad y1's for some constant c > 0. Then, the verifier may randomly choose a string z1 of length ![]() and has the probability c to win the game with this string z1. If this game on x is played repeatedly for a number of times and the prover is able to win the game consistently, then the verifier is more convinced that x is indeed in A (or, the verifier is extremely unlucky). This type of probabilistic game is called a probabilistic interactive proof system or, simply, an interactive proof system. The main difference between the probabilistic proof systems and the deterministic proof systems described earlier is that the verifier is allowed to use a random number generator to help him/her to compute new strings yi, as well as verifying the final accepting condition. That is, an interactive proof system for a set A is a proof system with the following properties:
and has the probability c to win the game with this string z1. If this game on x is played repeatedly for a number of times and the prover is able to win the game consistently, then the verifier is more convinced that x is indeed in A (or, the verifier is extremely unlucky). This type of probabilistic game is called a probabilistic interactive proof system or, simply, an interactive proof system. The main difference between the probabilistic proof systems and the deterministic proof systems described earlier is that the verifier is allowed to use a random number generator to help him/her to compute new strings yi, as well as verifying the final accepting condition. That is, an interactive proof system for a set A is a proof system with the following properties:
- The verifier has the power of a polynomial-time PTM, and the prover has the power of a PTM, without a limit on time or space bound.
- If an instance x is in A, then the prover is able to win the game of x with probability
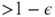 ; and if
; and if 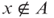 , then the probability that the prover is able to win the game of x is
, then the probability that the prover is able to win the game of x is 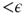 , where ε is a constant strictly less than 1/2.1
, where ε is a constant strictly less than 1/2.1
We look at some examples before giving the formal definition of interactive proof systems.
Example 10.1
Example 10.2
The above two examples demonstrate simple interactive proof systems for some problems in coNP that are not known to be complete for coNP. The next example shows a more complicated interactive proof system for a ![]() -complete problem, with a hint of the general theorem that all problems in PSPACE have interactive proof systems (Theorem 10.26).
-complete problem, with a hint of the general theorem that all problems in PSPACE have interactive proof systems (Theorem 10.26).
Example 10.3
Weak Interactive Proof System for PERM.
Input: An ![]() Boolean matrix A and an integer q. (The prover needs to prove that
Boolean matrix A and an integer q. (The prover needs to prove that ![]() .)
.)
Initially, let ![]() and
and ![]() .
.
Stage i, ![]() . Ai is an
. Ai is an ![]() matrix. The prover sends integers
matrix. The prover sends integers ![]() ,
, ![]() , to the verifier, where Bi,j is the submatrix of Ai obtained by deleting the first row and the jth column of Ai. Next, the verifier verifies that
, to the verifier, where Bi,j is the submatrix of Ai obtained by deleting the first row and the jth column of Ai. Next, the verifier verifies that
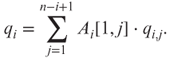
If the above equation does not hold, then the verifier rejects the input (A,q). Otherwise, the verifier chooses a random ![]() and lets
and lets ![]() and
and ![]() . He/she sends
. He/she sends ![]() and
and ![]() to the prover and goes to the next stage.
to the prover and goes to the next stage.
Stage n. The verifier has a ![]() matrix An and an integer qn. The verifier accepts the input if and only if
matrix An and an integer qn. The verifier accepts the input if and only if ![]() .
.
Assume that ![]() . Then the prover can always compute the correct values
. Then the prover can always compute the correct values ![]() at each stage i and, hence, can prove that
at each stage i and, hence, can prove that ![]() with probability 1.
with probability 1.
On the other hand, when ![]() , the error probability could be very large. More precisely, assume that at stage i,
, the error probability could be very large. More precisely, assume that at stage i, ![]() . Then, the prover could give
. Then, the prover could give ![]() correct values
correct values ![]() and only one incorrect value qi,j and could still satisfy (10.1). The probability that the verifier chooses this incorrect value to be
and only one incorrect value qi,j and could still satisfy (10.1). The probability that the verifier chooses this incorrect value to be ![]() is
is ![]() . As a whole, the probability that all pairs
. As a whole, the probability that all pairs ![]() are incorrect in all stages i is only
are incorrect in all stages i is only ![]() . Thus, the above proof system is too weak.
. Thus, the above proof system is too weak.
To remedy this problem, we modify the above proof system to reduce the error probability. Let us call a pair (C,r) of a matrix C and an integer r incorrect if ![]() . We have just seen that if at each stage i, the verifier only recursively tests the correctness of a random pair
. We have just seen that if at each stage i, the verifier only recursively tests the correctness of a random pair ![]() , then the error probability is too large. On the other hand, if the verifier recursively tests every pair
, then the error probability is too large. On the other hand, if the verifier recursively tests every pair ![]() at stage i, then it would take an exponential amount of time. The idea here is to combine all
at stage i, then it would take an exponential amount of time. The idea here is to combine all ![]() pairs
pairs ![]() to create a single pair that, with a large probability, is incorrect as long as one of the original pairs is incorrect. Therefore, the total number of pairs
to create a single pair that, with a large probability, is incorrect as long as one of the original pairs is incorrect. Therefore, the total number of pairs ![]() considered is polynomially bounded, and yet the error probability is kept small.
considered is polynomially bounded, and yet the error probability is kept small.
Interactive Proof System for PERM.
Input: (A,q).
Choose a large prime number p such that ![]() . (It could be done in polynomial time by the verifier; or, the prover could send the prime number, together with a short proof that it is indeed a prime, to the verifier.)
. (It could be done in polynomial time by the verifier; or, the prover could send the prime number, together with a short proof that it is indeed a prime, to the verifier.)
Let ![]() and
and ![]() .
.
Stage i, ![]() . The prover needs to prove that
. The prover needs to prove that ![]() .
.
Substage ![]() . The prover finds
. The prover finds ![]() ,
, ![]() and sends them to the verifier, where Bi,j is the submatrix of Ai obtained by deleting the first row and the jth column of Ai. Next, theverifier verifies that
and sends them to the verifier, where Bi,j is the submatrix of Ai obtained by deleting the first row and the jth column of Ai. Next, theverifier verifies that

If the above equation does not hold, then the verifier rejects the input (A,q). Otherwise, let ![]() and
and ![]() , and go to substage
, and go to substage ![]() .
.
Substage ![]() ,
, ![]() . The verifier forms an
. The verifier forms an ![]() linear-polynomial matrix
linear-polynomial matrix
and sends D(x) to the prover, asking forits permanent f(x) (a polynomial of degree ![]() ). When the verifier receives the permanent polynomial f(x) from the prover, he/she checks that
). When the verifier receives the permanent polynomial f(x) from the prover, he/she checks that ![]() and
and ![]() ; if either equation fails, he/she rejects the input. Otherwise, the verifier chooses a random integer
; if either equation fails, he/she rejects the input. Otherwise, the verifier chooses a random integer ![]() and let
and let ![]() (i.e., C is the
(i.e., C is the ![]() integer matrix obtained by substituting the integer a for the variable x in D) and
integer matrix obtained by substituting the integer a for the variable x in D) and ![]() .
.
At the end of substage ![]() , let
, let ![]() and
and ![]() .
.
Stage n. The verifier has a ![]() matrix An and an integer qn. The verifier accepts the input if and only if
matrix An and an integer qn. The verifier accepts the input if and only if ![]() .
.
First notice that an ![]() Boolean matrix A must have
Boolean matrix A must have ![]() , and so, for any
, and so, for any ![]() ,
, ![]() implies
implies ![]() . Thus, we do not lose any generality using arithmetic modulo p. (In the following lemma, we say (C,r) is incorrect if and only if
. Thus, we do not lose any generality using arithmetic modulo p. (In the following lemma, we say (C,r) is incorrect if and only if ![]() .) Next, we observe again that if
.) Next, we observe again that if ![]() , then the prover can always compute correct permanent values, including the permanent f of the polynomial matrix D in each substage
, then the prover can always compute correct permanent values, including the permanent f of the polynomial matrix D in each substage ![]() , and wins the game with probability 1. We only need to prove that when
, and wins the game with probability 1. We only need to prove that when ![]() , the probability of the prover winning the game is small.
, the probability of the prover winning the game is small.
Lemma 10.4
Proof
We observe that if ![]() is incorrect, then after substage
is incorrect, then after substage ![]() , one of the pairs
, one of the pairs ![]() is incorrect. Now, following the above lemma, the error in the pair
is incorrect. Now, following the above lemma, the error in the pair ![]() at stage i will be passed to the next pair
at stage i will be passed to the next pair ![]() at stage i + 1 with probability
at stage i + 1 with probability ![]() . The total error probability of the above interactive proof system is thus bounded by
. The total error probability of the above interactive proof system is thus bounded by
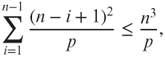
which is negligible when n is reasonably large.
From the above examples, we can see that an interactive proof system consists of an honest verifier who wants to learn whether or not a given instance x is in a set A and an unreliable prover whose task is to answer questions of the verifier to maximize his winning probability. As the prover is potentially treacherous, it is the verifier's job to detect the cheating to minimize the error probability. Thus, it is natural to define the interactive proof systems from the verifier's point of view, that is, we define the verifier as a probabilistic machine and let the prover take the role of an oracle. Formally, we define an interactive Turing machine to be a polynomial time oracle PTM Mv that uses an oracle function fp with the following special rule of making queries: The machine Mv makes a query y to the oracle fp by writing on the query tape (1) the input x, (2) the whole history of queries and answers exchanged between the machine Mv and the oracle fp, and (3) the new query y. (This special rule reflects the assumption that the prover can send a message yi based on the input x as well as the history of the messages exchanged between the prover and the verifier.) Note that the polynomial-time bound on Mv implies that it can only work with polynomial-length-bounded oracle functions fp. The notion of interactive proof systems can be defined by interactive TMs, working with unreliable oracles. (See Exercise 10.1 for an alternative formulation of the notion of interactive proof systems.)
Definition 10.5
The time complexity of an interactive TM is restricted to be polynomially bounded. In addition to the time complexity, an important complexity measure of an interactive proof system ![]() is the number of queries made by Mv to the oracle fp. Recall that a computation of a probabilistic oracle machine M, relative to an oracle f, is a sequence of successive configurations of Mf, from a starting configuration to a halting configuration. We define the number of rounds of a computation of an interactive proof system
is the number of queries made by Mv to the oracle fp. Recall that a computation of a probabilistic oracle machine M, relative to an oracle f, is a sequence of successive configurations of Mf, from a starting configuration to a halting configuration. We define the number of rounds of a computation of an interactive proof system ![]() to be the number of messages (queries and answers) exchanged between the machine Mv and the oracle fp in this computation. For an integer function r, we say that a set A has an r(n)-round interactive proof system if there exists an interactive proof system
to be the number of messages (queries and answers) exchanged between the machine Mv and the oracle fp in this computation. For an integer function r, we say that a set A has an r(n)-round interactive proof system if there exists an interactive proof system ![]() for A such that the number of rounds of all the computations of the system
for A such that the number of rounds of all the computations of the system ![]() on all x is bounded by
on all x is bounded by ![]() .3
.3
Definition 10.6
Similar to the probabilistic complexity classes RP and BPP, the classes IP and IPk remain the same if we change the error bound 1/4 to any constant ![]() .
.
Proposition 10.7
Proof
Finally, we observe the simple relations that ![]() and
and ![]() , and that the problems
, and that the problems ![]() and QNR of Examples 10.1 and 10.2 above are both in
and QNR of Examples 10.1 and 10.2 above are both in ![]() .
.
10.2 Arthur–Merlin Proof Systems
In order to analyze the computational power of interactive proof systems, we first study a weaker type of probabilistic proof system called the Arthur–Merlin proof system. An Arthur–Merlin proof system is similar to an interactive proof system where Arthur is a verifier with the power of a polynomial-time PTM and Merlin is a prover, except that Merlin is even more powerful than an ordinary prover so that he is able to read the whole history of the computation of Arthur on the given input, including the random numbers generated by Arthur. If we examine the interactive proof systems of Examples 10.1 and 10.2, we can see that the secrecy of the random bits used by the verifier is critical to the correctness of the system. Indeed, if in Example 10.1 the prover knows the random bit b chosen by the verifier, then he/she can always win the game by sending back the bit b, regardless of whether ![]() or not. Thus, the extra power of Merlin appears to be a strong restriction to the notion of interactive proof systems. Later, however, we will show that this restriction is not really so strong and that the two notions of proof systems are essentially equivalent. Yet, the simplicity of the Arthur–Merlin proof systems allows us to perform detailed analysis of its computational power.
or not. Thus, the extra power of Merlin appears to be a strong restriction to the notion of interactive proof systems. Later, however, we will show that this restriction is not really so strong and that the two notions of proof systems are essentially equivalent. Yet, the simplicity of the Arthur–Merlin proof systems allows us to perform detailed analysis of its computational power.
As Merlin is so powerful that Arthur is not able to hide his random numbers from Merlin, we may as well require that in an Arthur–Merlin proof system, Arthur always sends the random numbers he used to Merlin. Furthermore, Merlin can alwayssimulate Arthur's computation to compute the next query to be asked by Arthur from the history of the computation and the new random numbers received from Arthur. Thus, Arthur really does not have to send Merlin anything except the new random numbers generated by the random number generator. In other words, Arthur really plays a passive role whose only task is to verify, at the end, whether the computation satisfies a predetermined condition and whether to accept the input. Formally, we define an Arthur machine to be an interactive TM such that
- each new query of Arthur is simply a new sequence of random bits; and
- every random number generated by Arthur must be sent to Merlin as a query, even if Arthur does not expect an answer from Merlin (so that the last random number generated by Arthur counts as one round of communication between the two players).
To understand how such a simplistic communication protocol could work, it is helpful to review the interactive proof system of Example 10.3 for the problem PERM and observe that it is actually an Arthur–Merlin system. In particular, at each substage ![]() ,
, ![]() , the verifier only needs to verify that the answer f satisfies the two equations,
, the verifier only needs to verify that the answer f satisfies the two equations, ![]() and
and ![]() , and then sends a random number
, and then sends a random number ![]() to the prover. At the next substage, the prover can compute the matrix D by itself and sends its permanent f to the verifier.
to the prover. At the next substage, the prover can compute the matrix D by itself and sends its permanent f to the verifier.
Definition 10.8
The notion of the number of rounds in an Arthur–Merlin proof system is defined exactly the same as that of an interactive proof system. Here, we distinguish the proof systems in which Merlin sends the messages first from those in which Arthur sends the messages first.
Definition 10.9
Again, the classes AM and ![]() remain unchanged for any constant error probability ε > 0. We omit the proof.
remain unchanged for any constant error probability ε > 0. We omit the proof.
Proposition 10.10
In the above, we have defined the Arthur–Merlin proof system from Arthur's point of view, that is, we view such a proof system as Arthur working with an unreliable oracle Merlin trying to prove that an instance x is in A. As Merlin knows every random bit Arthur uses and has the unlimited computational power to simulate Arthur's computation, we may also look at this proof system from Merlin's point of view. Namely, we may think that Merlin tries to convince Arthur, who is a passive verifier, that an instance x is in A by showing the complete probabilistic proof to him, where the two players share a common trustable random number generator. That is, Merlin can demonstrate the proof by playing both roles in the game: he nondeterministically generates his messages for himself and randomly generates messages for Arthur. To formalize this idea, we consider a new computational model of probabilistic NTMs.
A probabilistic NTM is an NTM M attached with a random number generator ϕ. The machine M has two nonstandard states: the nondeterministic state and the random state. When the machine enters the nondeterministic state, it generates a bit nondeterministically, and when it enters a random state, it obtains a random bit from the random number generator. We call a probabilistic NTM a Merlin machine if there exists a polynomial p such that for each input x, it always halts in ![]() moves.
moves.
To simplify the notion of the accepting probability of a Merlin machine, we assume that such a machine M has two extra read-only tapes, called the Merlin tape and the Arthur tape, in addition to the input/output/work tape. The Arthur tape is just the random-bit tape of a PTM, where a sequence of random bits is supplied by the random number generator ϕ. The Merlin tape contains the messages to be sent from Merlin to Arthur. We assume that when a Merlin machine enters the nondeterministic state, it reads the next bit from the Merlin tape and when the machine enters the random state, it reads the next bit from the Arthur tape. Thus a configuration of a Merlin machine consists of the following information: (1) the current state q, (2) the current string s in the input/output/work tape to the left of the tape head, (3) the current string t at and on the right of the tape head in the input/output/work tape, (4) the current string α on the Merlin tape (from the beginning cell to the cell scanned by the tape head), and (5) the current string β on the Arthur tape (from the beginning cell to the cell scanned by the tape head). We define the successor relation ![]() on configurations and the concept of accepting configurations similar to that for PTMs (see Section 9.2). In particular, a configuration
on configurations and the concept of accepting configurations similar to that for PTMs (see Section 9.2). In particular, a configuration ![]() in the random state (or in the nondeterministic state) has two successor configurations,
in the random state (or in the nondeterministic state) has two successor configurations, ![]() and
and ![]() (or, respectively,
(or, respectively, ![]() and
and ![]() ) for some states q0 and q1.
) for some states q0 and q1.
To define the notion of the accepting probability, we first define the accepting probability ![]() of a configuration c. For any configuration
of a configuration c. For any configuration ![]() , we let
, we let ![]() if q is an accepting state and
if q is an accepting state and ![]() if q is a rejecting state. If q is a regular deterministic state and c1 is the unique successor configuration of c, then let
if q is a rejecting state. If q is a regular deterministic state and c1 is the unique successor configuration of c, then let ![]() . If q is a random state and c0 and c1 are two successor configurations of c, then let
. If q is a random state and c0 and c1 are two successor configurations of c, then let ![]() be the average of
be the average of ![]() and
and ![]() . If q is a nondeterministic state and c0 and c1 are two successor configurations of c, then let
. If q is a nondeterministic state and c0 and c1 are two successor configurations of c, then let ![]() be the maximum of
be the maximum of ![]() and
and ![]() . For any input x, the accepting probability of a Merlin machine on x is equal to
. For any input x, the accepting probability of a Merlin machine on x is equal to ![]() , where cx is the starting configuration for x. We also write
, where cx is the starting configuration for x. We also write ![]() to denote the accepting probability
to denote the accepting probability ![]() of M on x. As a Merlin game always halts in polynomial time, the probability
of M on x. As a Merlin game always halts in polynomial time, the probability ![]() is well defined.
is well defined.
The concept of rounds can also be defined in a Merlin machine. We define a random round of a computation of a Merlin machine M to be a maximum-length sequence of configurations that are either in a deterministic state or in the random state. Similarly, a nondeterministic round of a computation of a Merlin machine M is a maximum-length sequence of configurations that are either in a deterministic state or in the nondeterministic state. For k ≥ 1, a k-round Merlin machine M is one all of whose computations have at most k random and nondeterministic rounds.
Proposition 10.11
Proof
It is interesting to observe that the above conversions between the two types of machines preserve the number of rounds in each machine.
10.3 AM Hierarchy Versus Polynomial-Time Hierarchy
In this section, we consider the complexity classes AMk of sets having Arthur–Merlin proof systems of a bounded number of rounds. It is clear that these classes form a hierarchy:
We are going to see that this hierarchy collapses to the second level. In addition, they are contained in the second level ![]() of the polynomial-time hierarchy.
of the polynomial-time hierarchy.
To begin with, we first give an alternating quantifier characterization for the AM hierarchy like that for the polynomial-time hierarchy in Theorem 3.8. Intuitively, a move by Merlin demonstrates a new piece of proof to Arthur, and so it corresponds to an existential quantifier ![]() , while a move by Arthur is simply a sequence of random bits, and to a probabilistic quantifier
, while a move by Arthur is simply a sequence of random bits, and to a probabilistic quantifier ![]() . (Recall that
. (Recall that ![]() means “for at least
means “for at least ![]() strings y of length m,” and
strings y of length m,” and ![]() is the abbreviation for
is the abbreviation for ![]() .)
.)
Recall that two predicates R1 and R0 are complementary if R1 implies ![]() .
.
Definition 10.12
A simple induction shows that complementary ![]() - and
- and ![]() -predicates are indeed complementary if
-predicates are indeed complementary if ![]() . We are going to show that if
. We are going to show that if ![]() , then the predicates
, then the predicates ![]() and
and ![]() are complementary AMk-predicates. Before we prove that, we need to show that the notion of complementary AMk-predicates remains unchanged with respect to different values r. This can be proved by the majority vote technique. As it is more involved than the proofs of Theorems 10.7 and 10.10, we give a complete proof below. In the following, we write
are complementary AMk-predicates. Before we prove that, we need to show that the notion of complementary AMk-predicates remains unchanged with respect to different values r. This can be proved by the majority vote technique. As it is more involved than the proofs of Theorems 10.7 and 10.10, we give a complete proof below. In the following, we write ![]() to mean “for more than
to mean “for more than ![]() numbers
numbers ![]() .”
.”
