Figure 11.2 Path px. The following property of L-reduction shows the precise relation between the corresponding approximation problems. (Recall the definition of r-APPROX-Π from Section 2.5.) From Proposition 11.35, we have the following relations: We know from Corollary 11.28 that there exists a number s > 1 such that the problem s-APPROX-3SAT is F in which each variable appears in at most three clauses, find a Boolean assignment to the variables of F to maximize the number of true clauses. We are going to show that for some constant δ > 0. From Lemma11.9, we know that there is a family Figure 11.3 Trees for fan-out, where the open circles denote new vertices. Figure 11.4 Graph H. There is a big class of approximation problems that can be proved to be NP-hard using the L-reduction. The following is another example. In Section 2.5, we divided the optimization problems into three classes, according to their approximability. The third class contains the problems with polynomial-time approximation schemes. The second class contains the problems for each of which there is a constant Next, we turn our attention to problems in the first class, the class of problems for which the corresponding approximation problems are NP-hard for all ratios r > 1. In the last section, we saw that the problem CLIQUE belongs to this class. We can actually further divide this class into subclasses according to the best approximation ratio r(n), where r(n) is a function of input size n. For instance, consider the following problem: It is known that SC has a polynomial-time approximation algorithm with approximation ratio Note that both the problems SC and CLIQUE belong to the first class of inapproximable optimization problems, but they still have different approximation ratios: CLIQUE is so hard to approximate that it is not approximable in polynomial time within ratio The problem SC is a fundamental problem for classifying optimization problems to the first class. We show an application below.Example 11.33
Proof
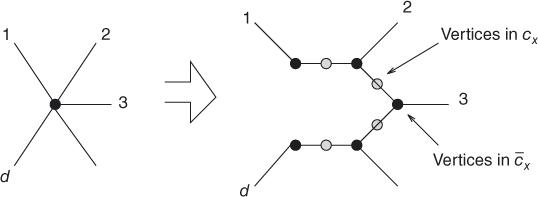
Example 11.34
Proof
Proposition 11.35
Proof
![]() and Γ has a polynomial-time linear approximation algorithm (meaning that the approximation ratio r is a constant), then Π also has a polynomial-time linear approximation algorithm.
and Γ has a polynomial-time linear approximation algorithm (meaning that the approximation ratio r is a constant), then Π also has a polynomial-time linear approximation algorithm.![]() and Γ has a (fully) polynomial-time approximation scheme, then Π has a (fully, respectively) polynomial-time approximation scheme.
and Γ has a (fully) polynomial-time approximation scheme, then Π has a (fully, respectively) polynomial-time approximation scheme.![]() -hard for NP. The L-reduction can pass this inapproximability result from 3-SAT to other problems. We first consider the following restricted version of 3-SAT, which is a fundamental problem for proving inapproximability results.
-hard for NP. The L-reduction can pass this inapproximability result from 3-SAT to other problems. We first consider the following restricted version of 3-SAT, which is a fundamental problem for proving inapproximability results.3SAT-3: Given a 3-CNF formula6
![]() S
S![]() -3. To prove this, we need a combinatorial lemma involving expanders. Recall that a d-regular graph
-3. To prove this, we need a combinatorial lemma involving expanders. Recall that a d-regular graph ![]() is an expander if
is an expander if![]()
![]() of d0-regular expanders of n vertices that have
of d0-regular expanders of n vertices that have ![]() , where d0 and
, where d0 and ![]() are global constants. In other words, for any
are global constants. In other words, for any ![]() , with
, with ![]() ,
, ![]() . We now prove a lemma using these expander graphs as a tool.
. We now prove a lemma using these expander graphs as a tool.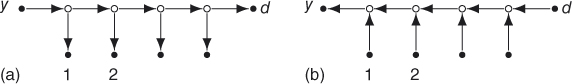
Lemma 11.36
Proof
Theorem 11.37
Proof
Theorem 11.38
Proof

VC-IN-CUBIC-GRAPHS (VC-CG): Given a graph G in which every vertex has degree exactly 3 (called a cubic graph), find the minimum vertex cover of G.
Theorem 11.39
Proof
![]() such that it is polynomial-time approximable with respect to ratio r0 but is inapproximable in polynomial time for any ratio
such that it is polynomial-time approximable with respect to ratio r0 but is inapproximable in polynomial time for any ratio ![]() unless
unless ![]() . We just showed that the maximum satisfiability belongs to this class. As L-reductions preserve linear-ratio approximation, all problems that are L-equivalent to 3-SAT belong to this class, including the problems VC-3, IS-3, 3SAT-3, and VC-CG studied above (cf. Exercise 11.16).
. We just showed that the maximum satisfiability belongs to this class. As L-reductions preserve linear-ratio approximation, all problems that are L-equivalent to 3-SAT belong to this class, including the problems VC-3, IS-3, 3SAT-3, and VC-CG studied above (cf. Exercise 11.16).SET COVER (SC): Given a finite collection
![]() of subsets of a set U of m elements, find a minimum cardinality subcollection of
of subsets of a set U of m elements, find a minimum cardinality subcollection of ![]() such that the union of all subsets in the subcollection covers U.
such that the union of all subsets in the subcollection covers U.![]() . In fact, this is the best-known result unless NP collapses to a deterministic subexponential time class.
. In fact, this is the best-known result unless NP collapses to a deterministic subexponential time class.Theorem 11.40
Proof
![]() for any ε > 0 (if
for any ε > 0 (if ![]() ), but SC has a polynomial-time approximation algorithm to achieve the approximation ratio
), but SC has a polynomial-time approximation algorithm to achieve the approximation ratio ![]() .
.SUBSET INTERCONNECTION DESIGNS (SID): Given a complete weighted graph H on vertex set X and given subsets
![]() of X, find a minimum-weight subgraph G (called a feasible subgraph) of H such that for every
of X, find a minimum-weight subgraph G (called a feasible subgraph) of H such that for every ![]() , G contains a spanning tree for Xi.
, G contains a spanning tree for Xi.
Theorem 11.41
Proof
Exercises
11.1 Show that co-RP = PCP![]() .
.
11.2 Show that there exists a constant ![]() such that for every Boolean function f with q variables, there exists a 3-CNF formula F with
such that for every Boolean function f with q variables, there exists a 3-CNF formula F with ![]() clauses such that f is satisfiable if and only if F is satisfiable.
clauses such that f is satisfiable if and only if F is satisfiable.
11.3 For each 3-CNF Boolean formula F, construct a constraint graph GF such that F is satisfiable if and only if GF is satisfiable.
11.4 Show that for d-regular graph G, ![]() .
.
11.5 Consider a d-regular graph ![]() . Show that for all
. Show that for all ![]() ,
,
11.6 Prove Lemma 11.14.
11.7 Prove Lemma 11.15.
11.8 Show that two different linear functions from ![]() to {0,1} differ in exactly a fraction 1/2 of locations.
to {0,1} differ in exactly a fraction 1/2 of locations.
11.9 Show Parseval's Identity used in the proof of Theorem 11.21.
11.10 Show that if for every Boolean function ![]() , there exist q Boolean functions
, there exist q Boolean functions ![]() , ...,
, ..., ![]() such that f is satisfiable if and only if
such that f is satisfiable if and only if ![]() is satisfiable, then
is satisfiable, then ![]() .
.
11.11 Show that for every Boolean function ![]() , there exist an alphabet
, there exist an alphabet ![]() and q functions
and q functions ![]() , ...,
, ..., ![]() from
from ![]() to {0,1} such that f is satisfiable if and only if
to {0,1} such that f is satisfiable if and only if ![]() is satisfiable.
is satisfiable.
11.12 The goal of steps (3) and (4) of the assignment testing proof system of Section 11.2.3 is to verify that a satisfies Ψ. Why cannot we just verify this by testing directly whether, for a random ![]() ,
, ![]() ?
?
11.13 (Multiple Prover Interactive Proof Systems). We extend the formulation of the interactive proof systems of Exercise 10.1 to multi-prover interactive proof systems in which more than one provers work together to convince the verifier that the input x is in the language L. To make it more powerful than the one-prover systems, the provers in a multi-prover system are not allowed to communicate with each other, once the proof system is activated. Formally, let ![]() be k DTMs and Mv be a polynomial-time PTM. We say
be k DTMs and Mv be a polynomial-time PTM. We say ![]() is a k-prover interactive protocol if they share a common read-only tape and for each i,
is a k-prover interactive protocol if they share a common read-only tape and for each i, ![]() ,
, ![]() and Mv share a communication tape Ti, and they compute in the same manner as the one-prover interactive protocol. That is, Mv and one of
and Mv share a communication tape Ti, and they compute in the same manner as the one-prover interactive protocol. That is, Mv and one of ![]() ,
, ![]() , take turns in being active. Suppose Mv is activated by
, take turns in being active. Suppose Mv is activated by ![]() ; then it reads the string on tape Ti, computes a string y and an integer j,
; then it reads the string on tape Ti, computes a string y and an integer j, ![]() , and then writes the string y on tape Tj and activates machine
, and then writes the string y on tape Tj and activates machine ![]() (or it may choose to halt and accept or reject). The activity of a prover
(or it may choose to halt and accept or reject). The activity of a prover ![]() is similar, except that it can only read from and write to tape Ti, that is, Mi cannot access tape Tj if
is similar, except that it can only read from and write to tape Ti, that is, Mi cannot access tape Tj if ![]() . We say that a set
. We say that a set ![]() has a k-prover interactive proof system with error bound ε if there exists a PTM Mv such that the following hold:
has a k-prover interactive proof system with error bound ε if there exists a PTM Mv such that the following hold:
- There exist k DTMs
 ,
,  ,
,  such that
such that  ,
,  ,
, 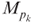 ,
, 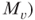 forms a k-prover interactive protocol and for each
forms a k-prover interactive protocol and for each 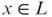 , the probability of these k + 1 machines together accepting x is at least
, the probability of these k + 1 machines together accepting x is at least  ; and
; and - For any k DTMs
 such that
such that  forms a k-prover interactive protocol and for any
forms a k-prover interactive protocol and for any  , the probability of these k + 1 machines together accepting x is at most ε.
, the probability of these k + 1 machines together accepting x is at most ε.
- Extend the above definition to allow the number k of provers being a function depending on the input size
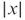 . Show that if a set L is in
. Show that if a set L is in 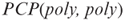 , then L has a k(n)-prover interactive proof system with error bound 1/4 for some polynomial function k.
, then L has a k(n)-prover interactive proof system with error bound 1/4 for some polynomial function k. - Prove that if L has a k(n)-prover interactive proof system with error bound 1/4 for some polynomial function k, then L has a two-prover interactive proof system with error bound 1/4.
- Show that if L has a two-prover interactive proof system with error bound 1/4, then
 .
.
11.14 Show that ![]() .
.
11.15 Extend the PCP characterization of NP to PSPACE and ![]() .
.
11.16 Show that the problems 2APPROX-3SAT, 2-APPROX-VC-3, and 4-APPROX-IS-3 are solvable in polynomial time.
11.17 Show that if ![]() , then the problem r-APPROX-CLIQUE is not polynomial-time solvable with ratio
, then the problem r-APPROX-CLIQUE is not polynomial-time solvable with ratio ![]() for all ε > 0.
for all ε > 0.
11.18 Consider the problem 2SAT-4: Given a 2-CNF formula in which each variable occurs at most four times, find a Boolean assignment to maximize the number of satisfying clauses. Show that there exists a real number r > 1 such that r-APPROX-2SAT-4 is ![]() -hard for NP.
-hard for NP.
11.19 Consider the problem STEINER MINIMUM TREES-IN-GRAPH (SMT-G): Given an edge-weighted graph G and a vertex subset S, find a minimum-weight subgraph interconnecting vertices in S. Show that there exists a real number r > 1 such that r-APPROX-SMT-G is ![]() -hard for NP.
-hard for NP.
11.20 Consider the problem SMT-IN-DIGRAPH (SMT-DG): Given an edge-weighted directed graph G, a vertex x, and a vertex subset S, find a minimum-weight directed tree rooted at x and connected to every vertex in S. Show that
- For some ρ > 0, there is no polynomial-time approximation algorithm with the approximation ratio
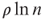 for SMT-DG unless
for SMT-DG unless  ; and
; and - For any ε > 0, there exists a polynomial-time approximation algorithm for SMT-DG with the approximation ratio nε.
11.21 Consider the problem LONGEST PATH (LP): Given a graph G and two vertices x and y in G, find the longest path between x and y in G. For any graph ![]() , let G2 be the graph with vertex set
, let G2 be the graph with vertex set ![]() and edge set
and edge set ![]() . Prove that there exists a path of length k between two vertices x and y in G if and only if there exists a path of length k2 between (x,x) and(y,y) in G2. Use this fact to find the best approximation ratio of any polynomial-time approximation algorithm for LP.
. Prove that there exists a path of length k between two vertices x and y in G if and only if there exists a path of length k2 between (x,x) and(y,y) in G2. Use this fact to find the best approximation ratio of any polynomial-time approximation algorithm for LP.
11.22 Show that 3-SAT is L-reducible to TSP with the triangle inequality.
11.23 Recall the problem SHORTEST COMMON SUPERSTRING (SCS) of Exercise 2.20(c). Show that 3-SAT is L-reducible to SCS.
11.24 Consider the problem MIN-BISECTION: Given a graph G, divide G into two equal halves to minimize the number of edges between the two parts. Study the approximability of this problem.
11.25 Show that the following problems have no polynomial-time approximation with approximation ratio ![]() for
for ![]() unless
unless ![]() :
:
- Given a finite collection
 of subsets of a set U of m elements, find a minimum subset intersecting every subset in
of subsets of a set U of m elements, find a minimum subset intersecting every subset in 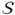 .
. - Given a finite collection
 of subsets of a set U of m elements, find a minimum cardinality subcollection of
of subsets of a set U of m elements, find a minimum cardinality subcollection of 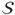 such that all subsets in the subcollection are disjoint and the union of all subsets in the subcollection covers U.
such that all subsets in the subcollection are disjoint and the union of all subsets in the subcollection covers U.
11.26 Show that for each of the following problems, there exists a real number ![]() such that the problem has no polynomial-time approximation with approximation ratio
such that the problem has no polynomial-time approximation with approximation ratio ![]() unless
unless ![]() :
:
- LP (defined above in Exercise 11.21).
- Given a system of n linear equations in m variables
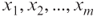 with integer coefficients and
with integer coefficients and 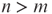 , find the minimum number of equations such that removal of them makes the remaining system feasible (in the sense that the system has at least one solution).
, find the minimum number of equations such that removal of them makes the remaining system feasible (in the sense that the system has at least one solution).
11.27 An optimization problem Π is A-reducible to an optimization problem Γ if there exist three polynomial-time computable functions h,g, and c such that (i) for any instance x of Π, h(x) is an instance of Γ; (ii) for any solution y to h(x), ![]() is a solution to x; and (iii) if the error ratio of y to h(x) is bounded by e, then the error ratio of
is a solution to x; and (iii) if the error ratio of y to h(x) is bounded by e, then the error ratio of ![]() to x is bounded by c(e), where the error ratio of a solution z to an instance x is
to x is bounded by c(e), where the error ratio of a solution z to an instance x is ![]() . Prove that if Π is A-reducible to Γ and Γ is approximable in polynomial time with ratio r(n), then Π is approximable in polynomial time with ratio
. Prove that if Π is A-reducible to Γ and Γ is approximable in polynomial time with ratio r(n), then Π is approximable in polynomial time with ratio ![]() .
.
Historical Notes
The celebrated result of the PCP characterization of NP started with the extension of the notion of interactive proof systems to the multi-prover proof systems (see Exercise 11.13) by Ben-Or et al. (1988). They defined MIP as the class of languages accepted by a multi-prover proof system in polynomial time. Fortnow et al. (1994) presented an equivalent formulation of the class MIP, based on the notion of randomized oracle TMs. Babai, Fortnow, and Lund (1991) showed that MIP = NEXPPOLY. Babai, Fortnow, Levin and Szegedy (1991) and Feige et al. (1996) further improved this result on problems in NP. Particularly, Feige et al. (1996) introduced a new notion of nonadaptive proof systems with restrictions on the number of random bits used and the number of queries asked by the verifier. Arora and Safra (1992, 1998) generalized it and called it the probabilistically checkable proof (PCP) system. They also introduced the idea of composing two proof systems into one and showed that ![]() . The final characterization of
. The final characterization of ![]() (Theorem 11.4) was proved by Arora et al. (1992, 1998). A complete proof along above line can be found in Arora's (1994) Ph.D. thesis (also in the first edition of this book).
(Theorem 11.4) was proved by Arora et al. (1992, 1998). A complete proof along above line can be found in Arora's (1994) Ph.D. thesis (also in the first edition of this book).
An important idea in the above development is to encode the proofs by some error-correcting coding scheme. For a complete treatment of the coding theory, see, for instance, Berlekamp (1968) and Roman (1992). The application of error-correcting coding to program checking has been studied by Blum and Kannan (1989), Blum, Luby, and Rubinfeld (1990), Gemmell et al. (1991), Lipton (1991), and Rubinfeld and Sudan (1996).
Our presentation of the proof of the PCP theorem follows from a short one given by Dinur (2007). This short proof uses the close relationship between the PCP theorem and approximation algorithms. For the general study of expander graphs and their applications to computer science, see Chapter 9 of Alon and Spencer (2011) and Hoory et al. (2006). The assignment tester has been studied in Dinur and Reingold (2006). The BLR test is from Blum, Luby, and Rubinfeld (1990). Radhakrishnan (2006) and Radhakrishnan and Sudan (2007) contain simplified proof of the graph powering step of Dinur's proof.
The study of approximation algorithms for optimization problems has been around for more than 30 years (see, e.g., Graham (1966) and Garey et al. (1972)). While a number of approximation algorithms have been found, the progress on negative results was slow before the 1990s. The first important work on inapproximability was given by Papadimitriou and Yannakakis (1991). They defined a class MAX-SNP that contains many NP-hard optimization problems that have polynomial-time linear approximation algorithms. They also studied complete problems for MAX-SNP under the L-reduction and showed that if any one of these problems has a polynomial-time approximation scheme, then every problem in MAX-SNP has a polynomial-time approximation scheme. The MAX-SNP-hardness was then widely used to establish the inapproximability results (see, e.g., Bern and Plassmann (1989)). In addition to the L-reduction, similar reductions, such as the A-reduction (Crescenzi and Panconesi, 1991) and AP-reduction (Crescenzi et al., 1995), have been proposed to prove inapproximability results. However, all these results relied upon the unproved assumption that r-APPROX-3SAT is not in P for some r > 1.
The breakthrough came in 1991, when Feige discovered the connection between the multi-prover proof systems of NP and approximability of the problem CLIQUE (see Feige et al. (1991, 1996); also see Condon (1993)). Following this piece of work and the PCP characterization of NP, the inapproximability results mushroomed. Arora et al. (1992, 1998) established that 3-SAT is inapproximable in polynomial time for some constant ratio r > 1 and, hence, all MAX-SNP-hard problems are inapproximable for some constant ratio. The best ratio 8/7 for the maximum 3-SAT problem was found by Hastad (1997) and Karloff and Zwick (1997). The problem VC-4 was shown to be one of the MAX-SNP-complete problems in Papadimitriou and Yannakakis (1991). Our result on VC-3 (Theorem 11.38) is from Du et al. (1998). Lund and Yannakakis (1994) built some new PCP systems to prove the inapproximability of problems beyond the class MAX-SNP, including the problem SET COVER. The optimum ratio ![]() for SET COVER in Theorem 11.40 was obtained by Feige (1996). Other results in this direction include Arora and Lund (1996), Bellare et al. (1993),Raz and Safra (1997), and Du et al. (1998). The hardest approximation problems belong to the maximum clique problem and the minimum chromatic number problem, which are known to be inapproximable with respect to ratio
for SET COVER in Theorem 11.40 was obtained by Feige (1996). Other results in this direction include Arora and Lund (1996), Bellare et al. (1993),Raz and Safra (1997), and Du et al. (1998). The hardest approximation problems belong to the maximum clique problem and the minimum chromatic number problem, which are known to be inapproximable with respect to ratio ![]() for any ε > 0 (Feige and Killian, 1996; Hastad, 1996). These inapproximability results also motivated some positive results. Among them, Arora (1996) proved that TSP on the Euclidean plane has a polynomial approximation scheme (see also Mitchell (1999)). Arora (1998) contains a survey of inapproximable results. Condon et al. (1993) and Kiwi et al. (1994) extended the PCP characterizations to classes PSPACE and PH. These papers and that by Ko and Lin (1995a, 1995b) also contain inapproximability results on optimization problems in PSPACE and PH.
for any ε > 0 (Feige and Killian, 1996; Hastad, 1996). These inapproximability results also motivated some positive results. Among them, Arora (1996) proved that TSP on the Euclidean plane has a polynomial approximation scheme (see also Mitchell (1999)). Arora (1998) contains a survey of inapproximable results. Condon et al. (1993) and Kiwi et al. (1994) extended the PCP characterizations to classes PSPACE and PH. These papers and that by Ko and Lin (1995a, 1995b) also contain inapproximability results on optimization problems in PSPACE and PH.
