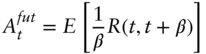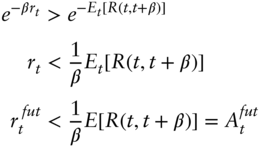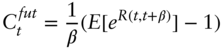This appendix builds on Appendixes A11.2 and A11.3 to explain the pricing of forward and futures rates and the futures‐forward rate difference in term structure models. All expectations here are also with respect to some risk‐neutral or pricing probabilities.

The first step in this Appendix is to show that the futures rate with respect to a term rate, like a Euribor futures rate in the text, is greater than the corresponding forward term rate.

The ‐year rate, years forward, , is the rate that equates the present value at time of receiving a unit of currency at time with the price of a ‐year zero coupon bond, ‐years forward, . Using continuously compounded rates,

(A12.1)

Furthermore, by Equation (A11.19),

(A12.2)

where is the futures price of that zero coupon bond.

Let be the realized ‐year rate at time . Then, by definition, the ‐year zero coupon bond price at that time, , is,

(A12.3)

and, by Equation (A11.14),

(A12.4)

Because of daily settlement payments of futures contracts, and following the same argument as in Appendix A11.2, which leads to Equation (A11.14), it can be shown that the futures rate, , corresponding to the ‐year zero coupon bond rate, is simply today's expectation of that bond rate at time ,

(A12.5)

By Jensen's inequality and Equation (A12.5),

(A12.6)

Stringing together Equations (A12.2), (A12.4), and (A12.6),

(A12.7)

Finally, focusing on the leftmost and rightmost terms of Equation (A12.7),

(A12.8)

as was to be proved.

The next step in this appendix is to show that the futures rate with respect to an average rate, like a one‐month SOFR (Secured Overnight Financing Rate) futures rate or a fed funds futures rate, is greater than the futures rate with respect to a term rate. This fact, combined with the result just proved, implies that futures rates with respect to average rates are also greater than the corresponding forward rates.

Let be the integral of the continuously compounded overnight rates from to , so that the average rate is . Once again, because of the daily settlement of futures contracts, today's futures rate on the average rate, , is today's expectation of the average at time ,

(A12.9)

By definition of the ‐year term rate at time , ,

(A12.10)

where gives the expectation as of time . Applying Jensen's inequality to (A12.10) and rearranging terms,

(A12.11)

where the third equation takes expectations of the second as of today, and the last equality follows from Equation (A12.9). Equation (A12.11) says that the futures rate on the average is greater than the futures rate on the term rates, as was to be proved.

The final step in this appendix is to show that the futures rate with respect to a compounded rate, like a three‐month SOFR futures rate, is greater than the futures rate with respect to an average rate. Once again, because of daily settlement, today's futures rate on a compounded rate, , is the expectation of that compounded rate in the future. Mathematically, in a continuously compounded version of Equation (12.10) in the text,

(A12.12)

By Jensen's inequality and the properties of the exponential function,

(A12.13)

Finally, combining Equations (A12.12), (A12.13), and the definition of the futures rate on the average in (A12.9),

(A12.14)

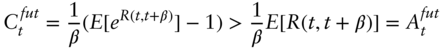
Hence, as was to be proved, the futures rate on a compounded rate is greater than the futures on an average rate.

To summarize, the financial insight is that, because of daily settlement, the forward price on a zero coupon bond is greater than the futures price on that bond. This result, from Chapter 11, plus a convexity effect in moving from price to rate, shows that the futures rate with respect to a term rate exceeds the corresponding forward term rate. Then, accounting for the convexity effects of moving to a futures rate with respect to an average rate or with respect to a compounded rate, these futures rates exceed the futures rate with respect to the term rate. The bottom line, then, is that all of the futures rates discussed in the chapter exceed the corresponding term forward rate.