Appendix 2

PRINCESS DIDO AND THE SINC FUNCTION

We’ll make an alliterative foray further into this forest by generalizing Dido’s “classical” Carthage problem somewhat. Recall that she formed a semicircular arc, with the (presumed) straight Mediterranean coastline as a diameter, thus enclosing a semicircular area for the city.

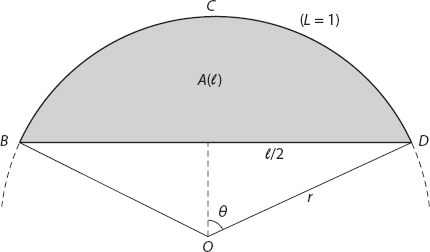
Clearly, the strip length L was shorter than the Mediterranean coastline, but what about the case where the available straight boundary is of variable length l < L; how does the area of the closed region vary with l? In fact, how do we know now that the semicircular area is still a maximum? We’ll do a little more mathematics and put in some numerical values just for fun, and work with l expressed in units of L, so that 0 < l < 1. Note that if l = 1 the enclosed area A is zero; the strip L = 1 is collinear with l, and if l = 0 the area of the circle is just 1/4π square units, half that of the area enclosed by the boundary and the completing semicircular arc. To investigate this, examine the circular segment BCD in Figure A2.1. The shaded area A(l) is enclosed by the circular arc of fixed unit length and the line segment of length l.

The arc subtends an angle 2θ at the center O, 0 < θ ≤ π. The arc length 2rθ = 1. In terms of θ the area of the shaded segment is

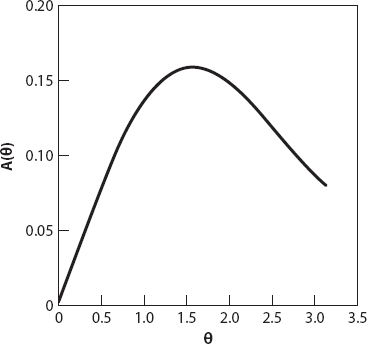
Note that, for π/2 < θ ≤ π this formula is still correct, but now cos θ < 0. A graph of A(θ) is shown below (Figure A2.2). It does indeed appear that the maximum enclosed area occurs when the region is a semicircle (θ = π/2). This is easily verified by noting that

Figure A2.1. Sector notation.

Figure A2.2. Area of sector as a function of θ (radians).

vanishes when θ = π/2 and θ ≈ 4.49 (the latter is well outside the interval of interest). And

But what is A(l)? Although (as indicated below) we cannot write down an exact expression for A(l), we can do so for A′(l), which is even better, for we can find values of θ corresponding to an extremum of A. Since

and

we readily obtain the expression

which is zero when θ = π/2 or tan θ = ±θ. (Note that dA/dl is expressed as a function of θ.) A graph of this derivative over the interval (0, π) shows that it is positive in (0, π/2), zero at θ = π/2, negative in (π/2, 2.029) and positive once more in (2.029, π). Thus A(l(θ)) has a maximum at θ = π/2 and a minimum at θ ≈ 2.029. when θ = π/2, A = 1/2π ≈ 0.159 and l = 2/π ≈ 0.64.

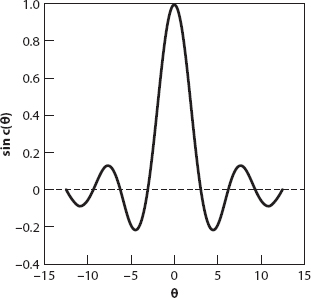
In using the result l = (sin θ)/θ we have made a natural connection between the two independent variables used above to express the area of the enclosed region. More precisely, the function

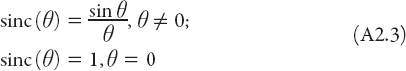
is known as the sine cardinal function, shown in Figure A2.3 for the interval (−4π, 4π).

The sinc function arises in many applications, from diffraction theory in optics to spectroscopy, information theory, and digital signal processing.

Unfortunately, there is no nice “inverse sinc function” to which we can appeal to express θ directly in terms of l. Nevertheless, in an entrepreneurial spirit, we shall attempt to find a reasonable and invertible approximation to this function, sufficient for our purposes. Since we are only interested in the interval [θ, π]we shall use instead the function

The graphs of these two functions are shown in Figure A2.4; f(θ) (the solid line) appears to be good enough for our purposes!

Figure A2.3. The sinc function.

Figure A2.4. The approximation f(θ).

In terms of this approximate function, it follows that since l ≈ f (θ), then

and hence from equation (A2.1),

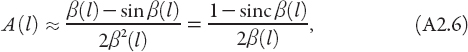
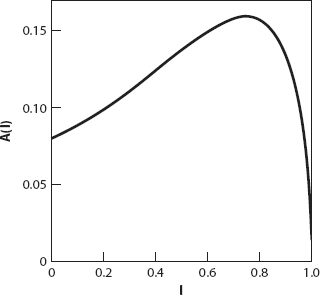
where . The approximation (A2.6) for A(l) is illustrated in Figure A2.5.

Figure A2.5. The approximation for A(l).

How does this compare with the exact results? The maximum value of A(l) according to equation (A2.6), occurs when

The only value of interest to us is when β = π, which corresponds to A ≈ 0.159, θ = π/2 and l = 0.75. Therefore we see that the approximation is “spot on” for the maximum area and where it occurs, but it overestimates the corresponding value of l by about 17%.

Comment: The definition (A2.3) is sometimes called the unnormalized sinc function. The normalized sinc function is defined as

because it may be shown that