Appendix 12

THE EARTH AS VACUUM CLEANER?

How effective is the Earth at clearing a path through “space matter” in its vicinity? This is of interest, of course, with regard to possible close encounters with asteroids, as discussed in Chapter 24. In order to get a handle on this problem, one major task is to determine how effective the Earth is at capturing “errant” asteroids. In order to do so, we will use some elementary physical principles and properties of conic sections.

Because of the gravitational attraction of the Earth (or any other sufficiently massive body), it can in principle “pull in” objects that are not traveling directly toward a head-on collision. This results in a capture cross section (CCS) that is at least as large as its geometric cross section (GCS). It is clear that this will depend (in particular) on the speed of the object relative to the Earth; something “whizzing by” our planet at high speed is less likely to be captured than a much slower object on the same path.

We can reduce this to a simple “two-body” problem by ignoring, for now, the rest of universe (as I so often do). The approach here is based on the article by Tatum (1997) [47]. Essentially, we consider the trajectory of the asteroid to be such that the gravitational attraction of the Earth is the dominant mechanism in this encounter. This is reasonable since the force of attraction of the Earth is ten times that of the sun at a distance of about 52,000 miles, or 13 Earth radii from its center, and about 1700 times that of the moon at this same distance. Under this assumption we can regard the trajectory of the asteroid as a hyperbolic one about a stationary Earth. Of course, both objects are in elliptical orbits around the sun, but in this “geocentric model” a hyperbolic orbit around the Earth is perfectly adequate for a “back of the envelope” calculation such as this.

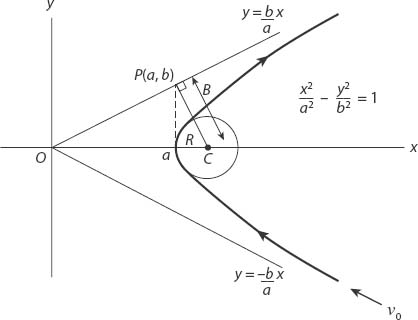
The notation is as follows (see Figure A12.1). The impact parameter B (no pun intended) is the closest distance of approach to Earth’s center that the asteroid would have it were on a straight line path, that is, one unaffected by Earth’s gravitational attraction (or more accurately, by their mutual gravitational attraction). Its initial speed (at “infinity”) is v₀ and the equation of its hyperbolic path is

a being the x-intercept and b the semi-transverse axis of the conjugate hyperbola.

Exercise: Using Figure A12.1, show that the impact parameter

The closest distance of approach on the hyperbolic orbit is called the perigee distance p, and if R is the radius of the Earth, the asteroid will collide with the Earth if p < R (the case p = R corresponds to grazing incidence). The GCS of the Earth is πR² and the potential CCS is defined to be πB². How do these two areas compare as a function of the initial speed v₀?

First we will need to calculate the potential energy Φ() of the asteroid under the action of the Earth’s gravitational field, where is the position vector of the asteroid relative to the Earth. The gravitational force , described by the famous inverse-square law, is directed along the radius vector joining the two bodies, and for a spherically symmetric force Φ is given by

Figure A12.1. The asteroid’s hyperbolic orbit drawn for “grazing incidence” with the Earth. The impact parameter B is the perpendicular distance of the asymptote from the Earth”s center of attraction at C. The radius of the Earth is R and the speed of the asteroid “at infinity” is v₀.

where m_a is the mass of the asteroid, M_e is the mass of the Earth, and G is the gravitational constant. At the perigee distance we suppose the asteroid speed relative to the Earth to be v_p, and we apply the principle of the conservation of energy to the asteroid, namely, that the

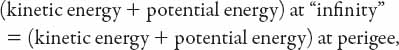
that is,

or, simplifying,

Another fundamental principle is the conservation of angular momentum,

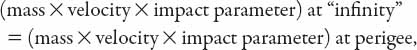
that is,

Elimination of v_p from these two equations results in

In this equation v_e = (2GM_e/R)^1/2 is the escape velocity from the surface of the Earth. To see this we equate the “escape” kinetic energy with the potential energy of a particle of unit mass at infinity. Thus

from which the result follows. Incidentally, v_e ≈ 11.2 km/s. Equation (A12.5) gives that the ratio of capture-to-geometric cross sections has a lower bound of one, as would be expected. It differs significantly from this value only when v₀ < v_e; thus for v₀ = 0.7v_e, B²/R² ≈ 3.

As pointed out by Tatum [47], there is a class of asteroids that approach our planet quite closely, and with small relative speeds, so the CCS/GCS ratio for these may be quite large. One such object is 1991 VG, which at that time was, at eight meters, the smallest astronomical object ever discovered (in orbit). The semi-major axis of its orbit is 1.04 astronomical units (≈ 1.50 × 10⁸ km; the mean Earth-sun distance is approximately 1 A.U.). The eccentricity of its orbit is 0.067 (Earth’s is 0.0167), which brings it inside the Earth’s orbit for part of the time. With this in mind, let the Earth move again (Oh, the power of mathematics!), in a circular orbit for simplicity, and imagine such an asteroid in a nearby circular orbit. Obviously we expect that these orbits will not be concentric in practice, but they may be close enough for a significant portion of the orbit to make this simplification useful. If the distance apart of the two orbits is less than the radius of the CCS, then the object can be captured. The closer the orbit is to that of the Earth, the smaller the relative speed and the larger the CCS becomes.

Suppose that the speed of the Earth in its orbit is V with orbit radius a, and the corresponding speed and orbit radius for the asteroid are V + δV and a + δa, respectively. Now Kepler’s third law of planetary motion states that the square of the orbital period P of a planet is directly proportional to the cube of the semi-major axis of its orbit (here a), or in terms of a constant of proportionality K, P² = Ka³. For a circular orbit, P = 2πa/V_e so that on eliminating P, Kepler’s law reduces to

Using differentials it follows that the relative difference in speed between the two objects is

From the earlier discussion we can identify δV, the relative difference in speeds, as v₀ and the difference in orbital radii, δa, as the impact parameter b. Using equation (A12.7) in (A12.5) we obtain (in the current notation)

The positive real root of this biquadratic equation is

In performing these calculations I found it simplest to write the term

since a/V = T/2π, where T is the period of the Earth’s orbit in seconds. We have already calculated the quantity 2GM/R from equation (A12.6). The result is δa ≈ 8.45 × 10⁵ km (δa ≈ 5.63 × 10⁻³ A.U.). In terms of the Earth’s equatorial radius R ≈ 6.38 × 10³ km, this is about 132 Earth radii, or approximately 2.2 times the Earth-moon semi-major axis.

From equation (A12.7) we find that the corresponding difference in orbital speed |δV| ≈ 0.085 km/s.

Exercise: Show from equations (A12.2) and (A12.5) that, for a grazing collision,

This shows that the perigee speed is quite sensitive to the impact parameter, varying as its square. Using this result we calculate the impact speed at a grazing collision to be ≈11.1 km/s, just a tiny bit less than the escape speed from the Earth. Since we have shown that the Earth sweeps out a toroidal volume of radius approximately 0.056 A.U. in its path around the sun, it can be thought of as a giant vacuum cleaner with CCS (132)² ≈ 1.74 × 10⁴ times that of the Earth’s GCS. Therefore any object moving in a circular orbit with radius between 0.9944 A.U. and 1.0056 A.U. will collide with (be captured by) the Earth. That’s some vacuum cleaner!