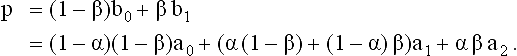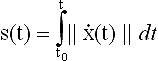2.1.1 Points and vectors

In general a point in n-space is fixed by its coordinates with respect to some Cartesian system¹. Nevertheless, we start our observations with affine aspects.

Let a = [α₁ … α_n]^t and b = [β₁ … β_n]^t denote two points, its difference v = b − ais called a vector, and one has b = a + v. In particular the column o = [0 … 0]^t = a − adenotes the null-vector.

Let a₀, …, a_ddenote d + 1 points in n–space, d ≤ n. The d vectors v_i = a_i- a₀, i = 1, …, d, are called linearly dependent if α₁v₁ + ˙˙˙ + α_dv_d = o, with at least one nonzero α_i, otherwise these vectors are called linearly independent. If v₁,…, v_dare linearly independent, then they span a linear space V^d, and the points a₀,…, a_dare called affinely independent and span an affine space A^d, d is called their dimension.

2.1.2 Affine systems

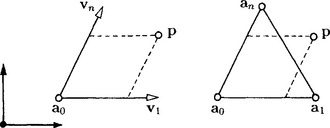
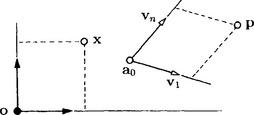
A point a₀and n linearly independent vectors v_idefine an affine system [a₀, v₁ … v_n] of the Aⁿ. In this system every point p = [η₁ … η_n]^t can be written uniquely as

(2.1)

where A = [v₁ … v_n] and x = [ξ₁ … ξ_n]^t. The ξ_iare called the affine coordinates of pwith respect to [a₀, v₁ … v_n], a₀is called the origin of the affine system.

To distinguish between points and vectors described by elements aof the ⁿ one may add a further coodinate, ∈, where

This convention can help to avoid mistakes in handling with points and vectors, see also Sub section 4.1 on homogeneous coordinates.

2.1.3 Barycentric coordinates

Let a₀,…, a_ndenote n + 1 affinely independent points of the Aⁿ and let v_i = a_i- a₀. One may rewrite equation (1) as

The ξ₀, …, ξ_nare called barycentric coordinates of pwith respect to the frame [a₀ … a_n].

Note that ξ₀+˙˙˙+ξ_n = 1. Note also that any n of the ξ_i, i ≠ j, represent affine coordinates of pwith respect to an affine system with origin a_j.

It follows immediately that a vector v = b−ahas barycentric coordinates v₀, …, v_nthat sum to zero, v₀+…+ v_n = 0. Note that the sum of the coordinates ξ_ior v_icorresponds to ∈ above.

2.1.4 Affine subspaces and parallelism

Let points a₀,…, a_d ∈ Aⁿ be given. The point

is called an affine combination of the points a_i. Let d ≤ n and let the points a_ibe affinely independent. Then they span a d-dimensional subspace ⊂ Aⁿ. With barycentric coordinates its points are written as affine combinations or with affine coordinates as

(2.2)

where v_i = a_i- a₀. This subspace is called a line, plane or hyperplane if d = 1, 2 or n − 1, respectively.

For any given pand given a₀, v₁, …, v_das elements of Rⁿ, the linear combination (2) represents a system of n linear equations for the ξ_i. It is solvable only if plies in the subspace.

Conversely, for varying ξ_ithe presentation (2) can be viewed as the solution of some linear system of n- d equations for an unknown p = [η₁ … η_n]^t. In particular, if d = n − 1, this system consists of one linear equation, say

or with barycentric coordinates of p

where additionally η₀ + … + η_n = 1.

Hyperplanes are called linearly independent if the rows [u₀u₁ … u_n] of their coefficients are linearly independent. Consequently, a subspace of dimension d of Aⁿ can be obtained as the intersection of n- d linearly independent hyperplanes. In particular, a point can be obtained as the intersection of n hyperplanes.

Note that the points of an affine subspace solve an inhomogeneous system, while their differences, the vectors, solve the corresponding homogeneous system.

A line p = a + λvis called parallel to a subspace B ⊂ Aⁿ if the coordinates of its points solve the homogeneous system corresponding to B. Moreover, two affine subspaces Aand Bare parallel if all lines of Aare parallel to B, or vice versa.

2.1.5 Affine maps and axonometric images

Equation (1) allows two interpretations. First, it expresses pwith respect to a new affine system [a₀, v₁ … v_n], where x = [ξ₁ … ξ_n]^t are the new coordinates of p. For example, the equation u₀ + u^tp = 0 of a hyperplane reads in the new coordinates q₀ + q^tx = 0, where q₀ = u₀ + u^ta₀and q^t = u^t A.

Second, it represents an affine map φ: x → p, where xand prepresent affine coordinates of two points. In particular, φ maps the origin o = [0 … 0] and the unit vectors²e_i = [δ_i,1 … δ_i,n]^t into a₀and v_i, i = 1,…, n, respectively. This important property defines the map uniquely and allows a simple design and investigation of an affine map. Note that φ maps the points xof the hyperplane q₀+ q^tx = 0 above into the points pof the hyperplane u₀+ u^tp = 0.

If the barycentric coordinate columns of points are denoted by the corresponding hollow letters, φ is written as

Note that affine maps preserve affine combinations, i.e. one has

and also preserve parallelism and the ratio of parallel distances, i.e. w = λvis mapped into [φw] = λ[φv].

If the v_iare linearly dependent, the map is degenerated. In particular, if η_{d +1} = … = η_n = 0 for all x, the map creates an axonometric image as used in descriptive geometry. Simple examples are the so-called cavalier and military projections, see [7].

2.1.6 Affine combinations and A-frame

Many algorithms in CAGD are based on repeated affine combinations. Consider two points, a₀and a₁. The affine combination

represents a point on the line spanned by a₀and a₁, and α represents an affine scale with α = 0 corresponding to a₀and α = 1 corresponding to a₁.

The term r[p; a₀a₁] = α/(1 − α) is called the ratio of pwith respect to a₀a₁.

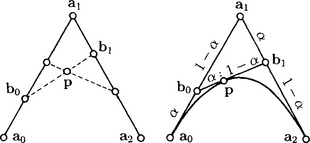
Consider three points a₀, a₁, a₂, and the affine combinations

both related by the same α, and the subsequent affine combination

(2.3)

Obviously, the resulting point pis symmetric in α and β. This means that α and β can be interchanged. This symmetry property is referred to as A-frame lemma and is a fundamental tool in de Casteljau’s work [6].

Let α = β. Then (3) reduces to

For fixed α the involved six points represent the so-called affine A-Frame, which is of great importance in Bernstein-Bézier methods. For varying α the point ptraces out a parabola, defined by a₀and a₂with tangents that intersects in a₁.

2.2.1 Quadrics in affine space

In an affine space a quadric Qconsists of all points xsatisfying a quadratic equation

where C = C^t is a symmetric non-zero matrix.

The intersection with a subspace is a quadric again. In particular, if the subspace is a line, one gets a pair of points. Note that these points can be real, coalescing or non-real.

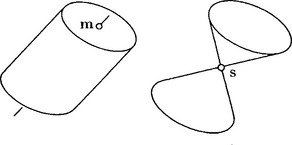
A point mis called a midpoint of Q, if Q(x, x) is symmetric with respect to m. This is the case for all solutions of

Note that a solution may not exist. If a midpoint slies on Q, it satisfies

and is called a singular point, while Qdegenerates to a cone.

2.2.2 Tangents and polar planes

A line L, given by x = q+ λv, where qis a point of Q, intersects Qin a second point. If both points coalesce, then Lis a tangent of Qat qand satisfies

If additionally v^t Cv = 0, then Llies completely on Q, and is called a generatrix of Q. Let v = q−x, then Lis a tangent if

This equation for xrepresents a plane, the tangent plane of Qat q.

Replacing qby an arbitrary point pgives

It represents the polar plane Pof the pole pwith respect to Q. It intersects Qin points qwith tangent planes through p. Note that these points qneed not be real. Note also that Q(p, x) is symmetric in pand x.

A pair of points p, xis called conjugate with respect to Qif Q(p, x) = 0. Hence the points of Qare self-conjugate with respect to Q. A pair of directions u, vis called conjugate with respect to Qif u^t Cv = 0. Conjugate elements play an important role in further investigations on quadrics in affine space.

Quadrics differ by the dimension of their midpoints or singularities, the dimension of their real generatrices and in affine space by the shape of their extensions to infinity.

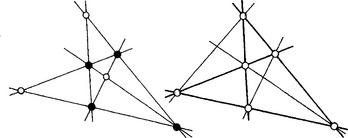
2.2.3 Pascal’s and Brianchon’s theorems

From the past there is a lot of knowledge on conic sections. Of particular interest are the following two theorems on conic sectioncs in the plane:

As a consequence of these theorems a conic section is uniquely determined by five points or five tangents in the plane.

Of particular interest are the theorems if pairs of consecutive points or tangents coalesce. E.g., let a₀, a₂denote two points of a conic section with tangents meeting at a point a₁. Let the points

(2.4)

span a third tangent. Its point of contact pis easily obtained from Brianchon’ theorem,

where α and β as in (4), see also [6].

2.3.1 Cartesian coordinates

An affine system [a₀, v₁… v_n] of Eⁿ is called Cartesian if³v_i⋅ v_j = δ_i,jand it is positively oriented if det[v₁… v_n] >0.

In Cartesian coordinates the distance of two points pand qis given by the length ||v|| of the vector v = q−p,

and the angle ϕ of two vectors uand vis given by

In particular, both vectors are called orthogonal if cos ϕ = 0, i.e. if u^tv = 0.

2.3.2 Gram-Schmidt orthogonalization

A Cartesian system [a₀, b₁… b_d] of a subspace or the Euclidean space itself can easily be constructed from an affine system [a₀, v₁… v_d] in Eⁿ with Gram-Schmidt’s orthogonalization by alternating computation of the coefficients λ_i,jand μ_ias follows:

Note that in a Cartesian system the dot product is written as u⋅ v = u^tv.

2.3.3 Euclidean motions and orthogonal projections

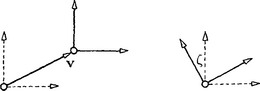
If the frame [a₀, v₁… v_n] is Cartesian, then (1) represents a Cartesian coordinate transformation or a Euclidean motion. Simple examples of motions in 3-space are the translation by vand the rotation around the 3-axis by an angle ζ, in matrices written as

respectively. In particular, let p = B_i(ϕ) xdescribe the rotation around the i-axis by some angle ϕ. Any motion in 3-space can be written as

where α, β, γ are the so–called Eulerian angles.

Any Euclidean motion followed by a map setting the coordinates η_{d +1}, …, η_nof the image pto zero results in an orthogonal projection onto some d–dimensional subspace.

It should be mentioned that orthogonal projections are more informative than simple parallel projections and much more informative then perspectivities. They are the only projections that map spheres to circles. Therefore orthogonal projections should be prefered in presenting technical objects.

2.3.4 Quadrics in Euclidean space

If the vectors v_iof the Cartesian system [a₀, v₁… v_n] are pairwise conjugate with respect to a quadric Q, then the v_iare principal axis directions of Qand C is a diagonal matrix.

One easily checks that for a conic section given by its equation a rotation by an angle α where

turns the coordinate axes into the axis directions of Qand transforms C into diagonal form.

2.4.1 Homogeneous coordinates

Let ξ₁, …, ξ_nbe affine coordinates of a point in Aⁿ with respect to an affine frame [a₀, v₁…v_n] as above. Set ξ_i = β_i/β₀with some β₀≠ 0. Then the β₀,β₁, …, β_nare homogeneous coordinates with respect to the given affine frame. Note that any non-zero multiple of the homogeneous coordinate column b = [β₀β₁… β_n]^t represents the same point. Note also that a point p = o is undefined. It represents the so-called forbidden point.

As before β_i = 0, i ≠ 0 represents the coordinate hyperplane ξ_i = 0. Further, β₀ = 0 represents points at infinity lying in the infinite or ideal hyperplane β₀ = 0. An affine space Aⁿ together with its ideal hyperplane forms a projective space Pⁿ, the projective extension of Aⁿ.

The advantage of this extension is the symmetry of homogeneous coordinates. Points at infinity are handled as points in any other plane. In particular, ideal points allow to intersect parallel lines and subspaces - at infinity. Note that any non-zero multiple of a vector represents the same point at infinity.

Note also that β₀ = 0 and β₀≠ 0 correspond to ∈ = 0 and ∈ = 1 in 1.2above.

2.4.2 Projective coordinates

Let O₀,…, O_dbe linearly independent columns of homogeneous coordinates of d +1 points in Pⁿ with integrated factors such that the sum O = O₀+⋅⋅⋅+ O_drepresents a given further point O called the unit point. These d +2 points determine a projective frame [O₀, …, O_d; O] of some projective subspace Sspanned by the points O₀,…, O_d. Any point p of this subspace can be represented by homogeneous projective coordinates x = [ξ₀… ξ_d]^t as

(2.5)

In particular, if o_i = [1, a^t_i]^t, and o = [1, a^t]^t then ais the center [a₀+ … + a_d]/d of the a_iand the ξ_iare a multiple of the barycentric coordinates of pwith respect to the affine frame [a₀… a_d].

2.4.3 Projective maps

The representation (5), with matrices written as ρp = Ax, allows two interpretations. First it represents the point p ∈ Sby new homogeneous coordinates p ∈S. Second it represents a projective map ψ: x → p of Sinto Pⁿ.

In particular, ψ maps the fundamental points x_i = [δ_0,i… δ_d,i]^t into o_i, i = 0, …, d and the unit point [1 … 1]^t into o. This determines the projective map uniquely - and A except for a common factor ρ.

Note that a projective map does not preserve parallelism and ratio in general, but it preserves the cross ratio

In particular, if then both pairs of points, xy and ob, lie in harmonic position. For example, let α be an affine scale, see 1.6, the pairs of points corresponding to −1, +1 and 0, ∞lie in harmonic position.

2.4.4 The procedure of inhomogeneizing

Any homogeneous equation in projective coordinates can easily be inhomogeneized by setting the homogeneizing coordinate to one. Any point is simply inhomogeneized to xor v, respectively.

Of particular interest is the application of this procedure to the point x of a projective line given by

Let ρ = 1 and let o = [α₀, α₀a^t]^t and b = [β₀, β₀b^t]^t. Then inhomogeneizing x = [ξ₀, ξ₀x^t]^t results in the affine combination

(2.6)

Similar results one gets by inhomogeneizing the points of a projective subspace (5) of higher dimension.

2.4.5 Repeated projective combinations

Repeated affine combinations and A-frames are often used in CAGD to compute polynomial curves and surfaces and can also be applied to the homogeneous coordinates of rational curves and surfaces. It is useful to inhomogeneize the resulting projective combinations by the procedure demonstrated above.

Moreover, after a first inhomogeneizing one can continue with the affine representation of the projective A-frame presented in Subsection 2.3. For more details on this procedure and its applications see [6].

2.4.6 Quadrics in projective space

In homogeneous or projective coordinates o the equation of a quadric Qsimplifies to

and the polarity is written as

Note that in homogeneous coordinates the midpoint of Qis the pole of the infinite plane. Note also that Qis a cylinder, if it has a singular point at infinity, etc.

2.4.7 Parametrizing a quadric and its equation

If a quadric Qis given by its equation , and q represents a point of , then

is a parametrization of Q, which is quadratic in the coordinates of p.

Setting, e.g., p = p₀ζ₀+⋅⋅⋅+p_{n −1}ζ_{n −1}, where the p_iare suitably choosen, it is also quadratic in the homogeneous ζ_i. Note that one may use any other representation for p, e.g., polar coordinates with the center q.

Conversely, the equation of a quadric in Aⁿ or Pⁿ depends on r = (n + 1)(n + 2)/2 homogeneous coefficients, the elements of . Let r − 1 pairs of conjugate points, p_iand q_i, be given, and let x denote some arbitrary point of Q. Then the r − 1 conditions together with form a homogeneous linear system for the r unknown coefficients of . Setting its determinant to zero results in the equation of Q.

2.6.1 Curve and surface

A curve x(t) in affine space Aⁿ is called regular at t₀if .

The curve x(t) is said to have a contact of order r at t₀with a surface given by the equation F(x) = 0, if it is regular at t₀and if F(x(t)) and its derivatives up to order r vanish at t = t₀. This means geometrically that the curve has r + 1 coalescing points in common with the surface at t = t₀. Note that this definition does not depend on the parametrization of x(t). Note also that by its geometric meaning the contact of order r is projectively invariant.

2.6.2 Curve and curve

A second curve y(s) given by the intersection of a number of surfaces contacts x(t) at t₀with order r if x(t) contacts all these surfaces at least with order r.

If the second curve y(s) is given parametrically, then both curves have contact of order r at t₀if there exists a regular reparametrization t = t(s), for x(t) such that the Taylor expansions of x(t(s)) and y(s) agree at t₀ = t(s₀) up to order r. This condition can be expressed by the chain rule as a system of r + 1 linear equations. Therefore contact of order r is referred to as chain rule continuity.

For example, a curve and its osculating circle at a point t₀have contact of order 2.

2.6.3 Surface and surface

Two surfaces have contact of order r at pif all regular curves that lie on one of them and meet phave at least contact of order r with the other surface. This means that after a suitable reparametrization the Taylor expansions of both surfaces at pagree up to order r.

2.6.4 Contur lines, reflection lines and isophotes

There are some important helpful curves to check the smoothness of surfaces visually.

A reflection line on a surface consists of all points pwhose connection with some fixed point e, the eye, is reflected into a ray that meets a given fixed line L.

An isophote on a surface consists of all points pwhose connection with the eye eincludes a fixed angle with the surface normal at p.

Contour lines are special isophotes. They consist of all points p, where the tangent plane meets e.

In general, on composite surfaces contur lines, reflection lines and isophotes have a lower order of contact than the surfaces themselves.

Note that all three kinds of curves can decay in parts. Note also that the use of infinite elements eand Lsimplifies their computation.

2.7.1 Arc length and osculating plane

Let a curve in E³ be given parametrically as x = x(t) and let

denote its point and first two derivatives at some t₀. If v₁≠ 0, its tangent at a₀is given by

If , its osculating plane at a₀is given by

The differential term is called the arc element of x(t), and the integral

its arc length, beginning at t₀. The arc length represents the natural parameter of the curve. In most cases it can only be computed approximately.

2.7.2 Curvature and torsion

The natural parameter s is very helpful to derive general curve properties. E.g., let α(s) and β(s) denote the angles of the tangent and the osculating plane at s with the tangent and osculating plane at some s₀, respectively, and let the prime ′ denote differentiation with respect to the arc length. Then

are called the curvature and the torsion of x(t) at s₀, respectively. Note that ρ = 1/κ represents the radius of the osculating circle.

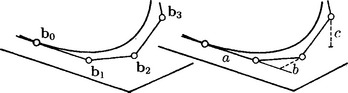
For example, a rational curve of degree n with Bézier points b_i = [β_i, β_ib^t_i]^t has the span of b₀, b₁as tangent at b₀, and the span of b₀, b₁, b₂as osculating plane at b₀. At t = 0 one has

where a, b, c denote the distances of b₁from b₀, of b₂from the tangent at b₀, and of b₃from the osculating plane at b₀, respectively.

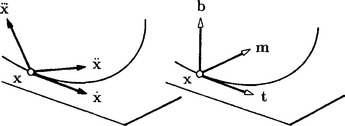
2.7.3 The Frenet frame

Schmidt’s orthogonalization applied to results in the so-called Frenet frame [tmb], which depends on t. One has

which is an important tool for further investigations, see [3],[5] and [9].

2.7.4 Curves on surfaces

Let a surface be given parametrically as

The lines u = fixed, v = fixed are called iso-lines. If the partial derivatives x_uand x_vare linearly independent, the surface normal is defined by

Let u = u(t) denote some curve in the u-plane then, in general, x = x(u(t)) represents a curve on the surface. The arc element ds of this curve is given by its square

where E = x^t_ux_u, F = x^t_ux_v, and G = x^t_vx_vare well–known as Gaussian first fundamental quantities. Note that ||x_uΛ x_v||² = EG - F².

2.7.5 Meusnier’s sphere and Dupin’s indicatrix

Consider all curves on a surface meeting a given point pwith a given tangent tthere. One has:

The osculating circles of these curves lie on a sphere (Meusnier’ sphere).

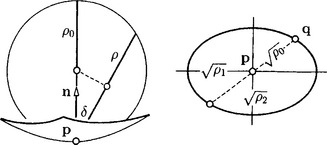
It follows that the radius of the osculating circle of a surface curve is given by ρ = ρ₀cosδ, where δ denotes the angle between the surface normal and the osculating plane and ρ₀is the radius of Meusnier’ sphere. The inverse κ₀ = 1/ρ₀is called the normal curvature of the surface at pin direction of t. Hence it is sufficient to know the curvature of one of these curves and the angle of its osculating plane with nto compute all others.

In general, the normal curvature κ₀differs for different t. For all tangent directions tat pconsider the points

of the tangent plane with distance from p. One has: The points qlie on a conic section with center p(Euler’s theorem).

This conic section is also known as Dupin’ indicatrix. Its axis directions are called the principal directions, and the corresponding values of κ = 1/ρ₀are called the principal curvatures of the surface at p, mostly denoted by κ₁ = 1/ρ₁and κ₂ = 1/ρ₂.

Note that Dupin’ indicatrix can be an ellipse, a pair of parallel lines or a hyperbola. In case of a hyperbola it has two real asymptotic directions. The normal curvature is zero there and ρ₀is infinite.

If κ₁ = κ₂, then Dupin’ indicatrix is a circle and pis called an umbilical or spherical point.

2.7.6 The curvatures of a surface

Because of its geometric meaning Dupin’ indicatrix and consequently the principal curvatures κ₁and κ₂at a point pdo not depend on the parametric representation of the surface.

The expressions

are called the Gaussian curvature and the mean curvature of the surface at p, respectively. Both give important information about the smoothness of a surface. Moreover, Gauss has shown that K depends on E, F, and G and their derivatives only. This means that K depends on the inner measurements on the surface only and is invariant under deformations of the surface that do not distort the measurement of lengths on the surface.

1. Adler, C. Modern Geometry. McGraw Hill; 1967.

2. Berger, M. Geometry 1 & 2. New York: Springer; 1987.

3. Boehm, W. Rational geometric splines. Computer Aided Geometric Design. 1987;4:67–77.

4. Boehm, W., Prautzsch, H. Numerical Methods. Berlin: A.K. Peters; 1992.

5. Boehm, W. Differential Geometry I & II, 3rd Edition. Wellesley: Academic Press; 1993.

6. Boehm, W. An affine representation of de Casteljau’s and de Boor’s rational algorithms. Computer Aided Geometric Design. 1993;10:175–180.

7. Boehm, W., Prautzsch, H. Geometric Concepts for Geometric Design. Boston: A.K. Peters; 1994.

8. Boehm, W. Circles of curvature for curves in space. Computer Aided Geometric Design. 1999;16:633–638.

9. do Carmo, M.P. Differential Geometry of Curves and Surfaces. Wellesley: Prentice Hall; 1976.

10. Coxeter, H.S.M. Introduction to Geometry. Englewood NJ: John Wiley & Son; 1969.

11. Farin, G. Curves and Surfaces for CAGD: a Practical Guide, 3rd Edition. New York: Academic Press; 1993.

12. Farin, G., Hansford, D. The Geometry Toolbox for Graphics and Modelling. Boston: AK Peters; 1998.

13. Farin, G. The Essentials of CAGD. Natick MA: AK Peters; 2000.

14. Hilbert, D., Cohn-Vossen, S. Geometry and the Imagination. Natick MA: Chelsea Publishing Co.; 1990.

15. Ding-yuan, L. Computational Geometry - Curve and Surface Modeling. New York: Academic Press Boston; 1992.

16. to appear Prautzsch, H., Boehm, W., Paluszny, M. Bézier and Spline Techniques. Springer; 2002.

17. Wylie, C. Introduction to Protective Geometry. Berlin/New York: McGraw Hill; 1970.