In Chapter 2, Practical Approach to Real-World Supervised Learning, we discussed different supervised classification techniques that are general and can be used in a wide range of applications. In the area of supervised non-linear techniques, especially in computer-vision, deep learning and its variants are having a remarkable impact. We find that deep learning and associated methodologies can be applied to image-recognition, image and object annotation, movie descriptions, and even areas such as text classification, language modeling, translations, and so on. (References [1, 2, 3, 4, and 5])
To set the stage for deep learning, we will start with describing what neurons are and how they can be arranged to build multi-layer neural networks, present the core elements of these networks, and explain how they work. We will then discuss the issues and problems associated with neural networks that gave rise to advances and structural changes in deep learning. We will learn about some building blocks of deep learning such as Restricted Boltzmann Machines and Autoencoders. We will then explore deep learning through different variations in supervised and unsupervised learning. Next, we will take a tour of Convolutional Neural Networks (CNN) and by means of a use case, illustrate how they work by deconstructing an application of CNNs in the area of computer-vision. We will introduce Recurrent Neural Networks (RNN) and its variants and how they are used in the text/sequence mining fields. We will finally present a case study using real-life data of MNIST images and use it to compare/contrast different techniques. We will use DeepLearning4J as our Java toolkit for performing these experiments.
Historically, artificial neural networks have been largely identified by multi-layer feed-forward perceptrons, and so we will begin with a discussion of the primitive elements of the structure of such networks, how to train them, the problem of overfitting, and techniques to address it.
A single neuron or perceptron is the same as the unit described in the Linear Regression topic in Chapter 2, Practical Approach to Real-World Supervised Learning. In this chapter, the data instance vector will be represented by x and has d dimensions, and each dimension can be represented as 
. The weights associated with each dimension are represented as a weight vector w that has d dimensions, and each dimension can be represented as 
. Each neuron has an extra input b, known as the bias, associated with it.
Neuron pre-activation performs the linear transformation of inputs given by:
The activation function is given by 
, which transforms the neuron input 
as follows:
Figure 1. Perceptron with inputs, weights, and bias feeding to generate outputs.
Multi-layered neural networks are the first step to understanding deep learning networks as the fundamental concepts and primitives of multi-layered nets form the basis of all deep neural nets.
We introduce the generic structure of neural networks in this section. Most neural nets are variants of the structure outlined here. We also present the relevant notation that we will use in the rest of the chapter.
Figure 2. Multilayer neural network showing an input layer, two hidden layers, and an output layer.
The most common supervised learning algorithms pertaining to neural networks use multi-layered perceptrons. The Input Layer consists of several neurons, each connected independently to the input, with its own set of weights and bias. In addition to the Input Layer, there are one or more layers of neurons known as Hidden Layers. The input layer neurons are connected to every neuron in the first hidden layer, that layer is similarly connected to the next hidden layer, and so on, resulting in a fully connected network. The layer of neurons connected to the last hidden layer is called the Output Layer.
Each hidden layer is represented by 
where k is the layer. The pre-activation for layer 0 < k
< l is given by:
The hidden layer activation for 
:
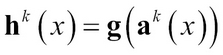
The final output layer activation is:
The output is generally one class per neuron and it is tuned in such a way that only one neuron activates and all others have 0 as the output. A softmax function with 
is used for giving the result.
Some of the most well-known activation functions that are used in neural networks are given in the following sections and they are used because the derivatives needed in learning can be expressed in terms of the function itself.
In this section, we will discuss the key elements of training neural networks from input training sets, in much the same fashion as we did in Chapter 2, Practical Approach to Real-World Supervised Learning. The dataset is denoted by D and consists of individual data instances. The instances are normally represented as the set 
. The labels for each instance are represented as the set 
. The entire labeled dataset with numeric or real-valued features is represented as paired elements in a set as given by 
.
Empirical risk minimization is a general machine learning concept that is used in many classifications or supervised learning. The main idea behind this technique is to convert a training or learning problem into an optimization problem (References [13]).
Given the parameters for a neural network as ? = ({W1, W2, … W l +1}, {b1, b2, …b L +1}) the training problem can be seen as finding the best parameters (?)such that
Where 
Stochastic gradient descent (SGD) discussed in Chapter 2, Practical Approach to Real-World Supervised Learning and Chapter 5, Real-time Stream Machine Learning, is commonly used as the optimization procedure. The SGD applied to training neural networks is:
- initialize ? = ({W1, W2, … Wl +1}, {b1, b2, …bL +1})
- for i=1 to N epochs
-
for each training sample (xt, yt)
// find the gradient of function
2 ?= ?+ a? //move in direction
-
for each training sample (xt, yt)
The learning rate used here (a) will impact the algorithm convergence by reducing the oscillation near the optimum; choosing the right value of a is often a hyper parameter search that needs the validation techniques described in Chapter 2, Practical Approach to Real-World Supervised Learning.
Thus, to learn the parameters of a neural network, we need to choose a way to do parameter initialization, select a loss function 
, compute the parameter gradients 
, propagate the losses back, select the regularization/penalty function O(?), and compute the gradient of regularization 
. In the next few sections, we will describe this step by step.
The parameters of neural networks are the weights and biases of each layer from the input layer, through hidden layers, to the output layer. There has been much research in this area as the optimization depends on the start or initialization. Biases are generally set to value 0. The weight initialization depends on the activation functions as some, such as tanh, value 0, cannot be used. Generally, the way to initialize the weights of each layer is by random initialization using a symmetric function with a user-defined boundary.
The loss function's main role is to maximize how well the predicted output label matches the class of the input data vector.
Thus, maximization 
is equivalent to minimizing the negative of the log-likelihood or cross-entropy:
We will describe gradients at the output layer and the hidden layer without going into the derivation as it is beyond the scope of this book. Interested readers can see the derivation in the text by Rumelhart, Hinton and Williams (References [6]).
Gradient at the output layer can be calculated as:
Where e(y) is called the "one hot vector" where only one value in the vector is 1 corresponding to the right class y and the rest are 0.
The gradient at the output layer pre-activation can be calculated similarly:
= – (e(y) – f(x))
A hidden layer gradient is computed using the chain rule of partial differentiation.
Gradient at the hidden layer 
Gradient at the hidden layer pre-activation can be shown as:
Since the hidden layer pre-activation needs partial derivatives of the activation functions as shown previously (g'(akxj)), some of the well-known activation functions described previously have partial derivatives in terms of the equation itself, which makes computation very easy.
For example, the partial derivative of the sigmoid function is g'(a) = g(a)(1 – g(a)) and, for the tanh function, it is 1 – g(a)2.
The aim of neural network training is to adjust the weights and biases at each layer so that, based on the feedback from the output layer and the loss function that estimates the difference between the predicted output and the actual output, that difference is minimized.
The neural network algorithm based on initial weights and biases can be seen as forwarding the computations layer by layer as shown in the acyclic flow graph with one hidden layer to demonstrate the flow:
Figure 3: Neural network flow as a graph in feed forward.
From the input vector and pre-initialized values of weights and biases, each subsequent element is computed: the pre-activation, hidden layer output, final layer pre-activation, final layer output, and loss function with respect to the actual label. In backward propagation, the flow is exactly reversed, from the loss at the output down to the weights and biases of the first layer, as shown in the following figure:
Figure 4: Neural network flow as a graph in back propagation.
The backpropagation algorithm (References [6 and 7]) in its entirety can be summarized as follows:
Compute the output gradient before activation:
For hidden layers k=l+1 to 1:
Compute the gradient of hidden layer parameters:
Compute the gradient of the hidden layer below the current:
Compute the gradient of the layer before activation:
In the empirical risk minimization objective defined previously, regularization is used to address the over-fitting problem in machine learning as introduced in Chapter 2, Practical Approach to Real-World Supervised Learning. The well-known regularization functions are given as follows.
