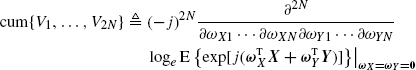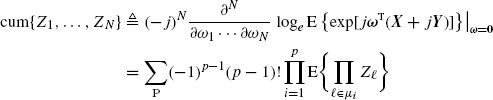1.4 Some Properties of Cumulants

In this section, some properties of cumulants that will be used in the subsequent chapters are reviewed. For comprehensive treatment of higher-order statistics of random variables and stationary and nonstationary signals see (Brillinger 1965, 1981), (Rosenblatt 1974), (Gardner and Spooner 1994), (Spooner and Gardner 1994), (Dandawaté and Giannakis 1994, 1995), (Boashash et al. 1995), (Napolitano 1995), (Izzo and Napolitano 1998a), (Napolitano and Tesauro 2011).

1.4.1 Cumulants and Statistical Independence

Theorem 1.4.1 If two real-valued random-variable vectors and are statistically independent, then

(1.190)

Proof: Let , and . The characteristic function of the random vector X factorizes into the product of the characteristic functions of X₁ and X₂. That is,

(1.191)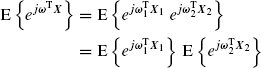

where the second equality is consequence of the statistical independence of the random vectors X₁ and X₂. Thus,

(1.192)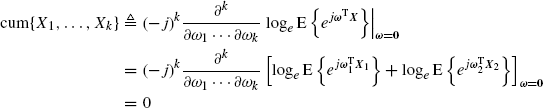

where the kth-order derivative of each of the two terms in the square brackets is zero since the first one depends only on , and the second one depends only on .

This result can be extended with minor changes to the case of complex-valued random-variable vectors.

As a consequence of Theorem 1.4.1, we have that if the stochastic process is asymptotically independent, that is, for every t the random variables x(t) and x(t + τ) are asymptotically (|τ|→ ∞) independent, then

(1.193)

where . In fact, if ||τ||→ ∞, then at least one τ_i→ ∞ and x(t + τ_i) becomes statistically independent of x(t).

1.4.2 Cumulants of Complex Random Variables and Joint Complex Normality

In this section, the non-obvious result is proved that the Nth-order cumulant for complex random variables defined in (Spooner and Gardner (1994) App. A) (see also (1.209)) is zero for N ≥ 3 when the random variables are jointly complex Normal (Napolitano 2007a App. E).

Let V = [V₁, ..., V_N, V_N+1, ..., V_2N]^T [X^T, Y^T]^T be the 2N-dimensional column vector of real-valued random variables obtained by the N-dimensional column vectors X [X₁, ..., X_N]^T, and Y [Y₁, ..., Y_N]^T of real-valued random variables. It is characterized by the 2Nth-order joint probability density function (pdf)

(1.194)

Its moment generating function is the 2N-dimensional Laplace transform

(1.195)

with , which is analytic in the region of convergence of the integral. The mean vector of V is

(1.196)

where μ_X and μ_Y are the mean vectors of X and Y, respectively. The covariance matrix is

(1.197)

where C_XX and C_YY are the covariance matrices of X and Y, respectively, and

(1.198)

is their cross-covariance matrix.

The 2Nth-order cumulant of the real random variables V₁, ..., V_2N is defined as

(1.199)

where ω_X [ω_X1, ..., ω_XN]^T and ω_Y [ω_Y1, ..., ω_YN]^T.

Let us consider, now, the N-dimensional complex-valued column vector Z = [Z₁, ..., Z_N]^T X + jY. It is characterized by the same 2Nth-order joint pdf f_V(v) of the 2N-dimensional real-valued vector V defined above.

Instead of considering the vector V, the following complex augmented-dimension vector

(1.200)

can be considered. Its mean vector and covariance matrix are given by

(1.201)

(1.202)

where

(1.203)

(1.204)

(1.205)

(1.206)

(1.207)

(1.208)

with and C_ZZ referred to as covariance matrix and conjugate covariance matrix, respectively.

The Nth-order cumulant of the complex random variables Z₁, ..., Z_N can be defined as (Spooner and Gardner 1994, App. A)

(1.209)

where ω [ω₁, ..., ω_N]^T and P are the set of distinct partitions of {1, ..., N} each constituted by the subsets {μ_i, i = 1, ..., p}. Note that since each complex variable Z_k is arbitrary, it can also be the complex conjugate of another complex variable. Such a definition turns out to be useful when applied to complex-valued stochastic processes or time series as shown in (Spooner and Gardner 1994, App. A), (Izzo and Napolitano 1998a), (Izzo and Napolitano 2002a). In particular, it is useful since it preserves the same relationship between moments and cumulants of real random variables (Leonov and Shiryaev 1959), (Brillinger 1965, 1981), (Brillinger and Rosenblatt 1967), as such a relationship is purely algebric. In addition, the characteristic function in (1.209) is an analytic function of the complex variables X_k + jY_k, k = 1, ..., N. In contrast, the characteristic function in (1.199) depends separately on X_k and Y_k and hence, in general, is not an analytic function of the complex variables X_k + jY_k. Finally, note that, for deterministic liner time-variant systems, input/output relationships in terms of cumulants defined as in (1.209) have the same form as that in terms of moments (Napolitano 1995), (Izzo and Napolitano 2002a).

Let Z be a N-dimensional column vector of jointly complex Normal random variables. That is, V is a 2N-dimensional column vector of jointly Normal real-valued random variables:

(1.210)

that can also be written in the complex form (Picinbono 1996), (van den Bos 1995)

(1.211)

where ζ₁ [z^T, z^H]^T, which is denoted as .

The moment-generating function (1.195) of f_V(v) is the 2N-dimensional Laplace transform

(1.212)

whose region of convergence is the whole complex space . Therefore, both characteristic functions involved in the cumulant definitions (1.199) and (1.209) can be expressed as slices of the moment-generating function Φ_V(s) given in (1.212). Specifically, in (1.199) we have

(1.213)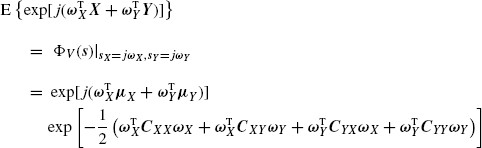

from which it follows that is a quadratic homogeneous polynomial in the real variables ω_X1, ..., ω_XN, ω_Y1, ..., ω_YN. As a consequence, we have the well-known result that jointly real-valued Normal random variables have kth-order cumulants of order k ≥ 3 equal to zero. In addition, in (1.209) we have

(1.214)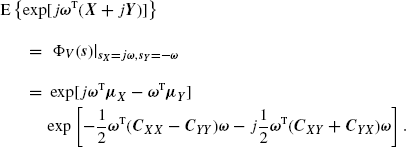

Hence, is a quadratic homogeneous polynomial in the real variables ω_i. Therefore, jointly complex Normal random variables are characterized by the fact that their cumulants of order N ≥ 3 defined as in (1.209) are equal to zero.