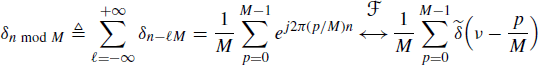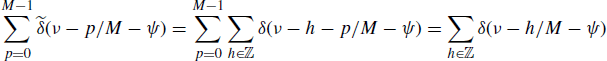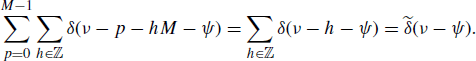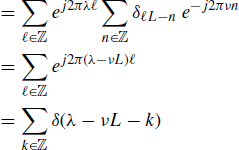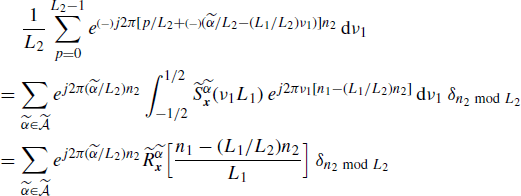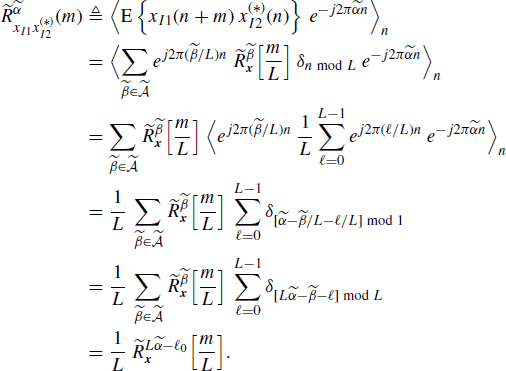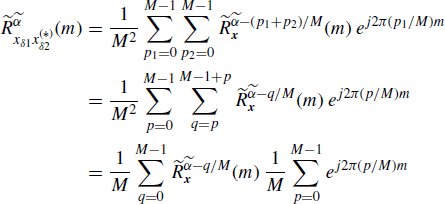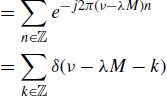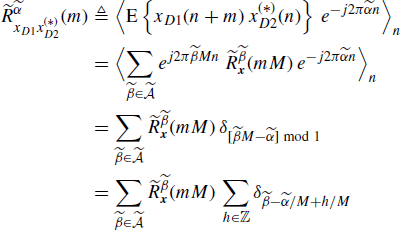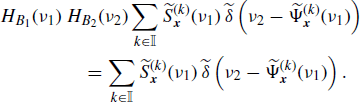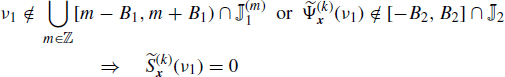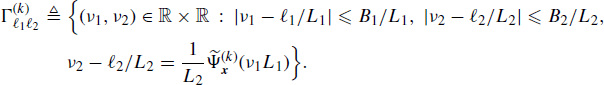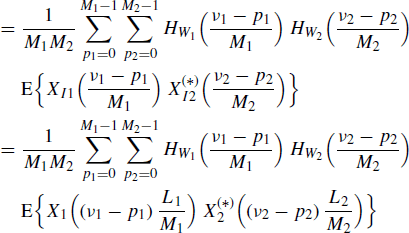5.11 Proofs for Section 4.10 “Multirate Processing of Discrete-Time Jointly SC Processes”

In this section, proofs of results of Section 4.10 are reported.

For future reference, let us consider the discrete-time sample train with sampling period M, its discrete Fourier series (DFS), and its Fourier transform:

(5.190)

where δ_m is the Kronecker delta, that is, δ_m = 1 if m = 0 and δ_m = 0 if m ≠ 0 and mod M denotes modulo operation with values in {0, 1, …, M − 1}. Thus, δ_{n mod M} = 1 if n = kM for some integer k and δ_{n mod M} = 0 otherwise.

Furthermore, in the sequel, the following identities are used

(5.191)

(5.192)

In the following proofs, the bounded variation assumption (4.192) allows to use the Fubini and Tonelli theorem (Champeney 1990, Chapter 3) to interchange the order of the integrals in ν₁ and ν₂.

5.11.1 Expansion (Section 4.10.1): Proof of (4.241), (4.242b), and (4.242c)

From the identity

(5.193)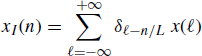

it follows that the impulse-response function of the LTV system that operates expansion is

(5.194)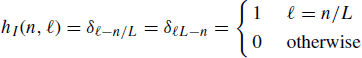

Thus, the transmission function is

(5.195)

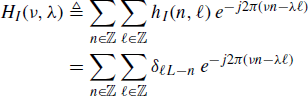
where in the last equality the Poisson's sum formula (Zemanian 1987, p. 189)

(5.196)

is used. Equation (4.242b) follows by using the definition (4.243) of , where equalities should be intended in the sense of distributions (generalized functions) (Zemanian 1987).

From (5.195), using the scaling property of the Dirac's delta δ(bt) = δ(t)/|b| (Zemanian 1987, p. 27) we have

(5.197)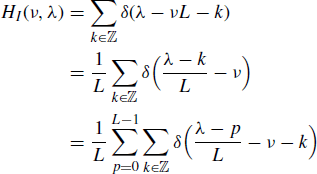

from which (4.242c) follows accounting for the definition of .

5.11.2 Expansion (Section 4.10.1): Proof of (4.250)

The inverse double Fourier transform of both sides of (4.248c) provides the cross-correlation of x_I1(n) and x_I2(n) (see (4.182) and (4.187))

(5.198)

The third equality in (5.198) follows from the Fourier pair

(5.199)

and the fourth equality is due to (5.190). The fifth equality in (5.198) is a consequence of the Fourier-transform pair (4.244)–(4.245).

By substituting n₁ = n + m and n₂ = n into (5.198), (4.250) immediately follows.

5.11.3 Expansion (Section 4.10.1): Proof of (4.253)

From (4.250) with L₁ = L₂ = L and using (5.190) it follows that

(5.200)

The sixth equality of (5.200) follows observing that for every there is at most one value of , say ₀ (depending on , , and L), such that , provided that . In fact, it results that

(5.201)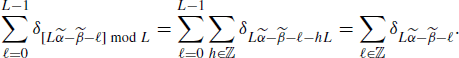

Thus, (4.253) immediately follows since is periodic in with period 1.

5.11.4 Sampling (Section 4.10.2): Proof of (4.261)

Let be M₁ = M₂ = M. Each process x_δi(n) is the product of the almost-cyclostationary discrete-time process x_i(n) and the (real-valued) periodic train δ_{n mod M} with Fourier series expansion given in (5.190). Thus, by using the discrete-time counterpart of (1.143) or (Napolitano 1995, eq. (46)) (specialized to 2 single-input single-output systems, second-order, and reduced-dimension) we have

(5.202)

from which, accounting for (5.190), one obtains (4.261).

In (5.202), in the second equality the variable changes p = p₁ and q = p₁ + p₂ are made and in the third equality the fact that is periodic in with period 1 is used, so that the sum over can be equivalently extended over .

5.11.5 Decimation (Section 4.10.3): Proof of (4.268), (4.269b), and (4.269c)

From the identity

(5.203)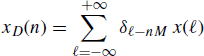

it follows that the impulse-response function of the LTV system that operates decimation is

(5.204)

Consequently, the transmission function is

(5.205)

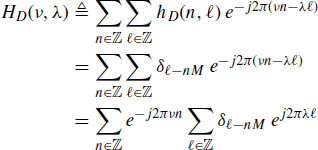
where in the last equality the Poisson's sum formula (5.196) is used. Equation (4.269b) follows by the definition of . From (5.205), using the scaling property of the Dirac delta, we have

(5.206)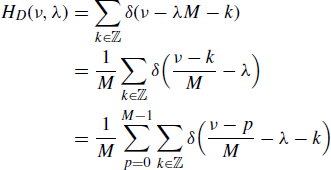

from which (4.269c) follows accounting for the definition of .

5.11.6 Decimation (Section 4.10.3): Proof of (4.277)

By using (4.275) we have

(5.207)

where, in the fourth equality, the Fourier-transform pairs (see (4.270) and (4.272))

(5.208)

(5.209)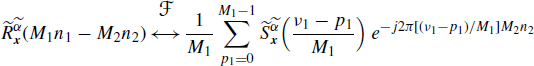

are accounted for.

Equation (4.277) follows by substituting n₁ = n + m and n₂ = n.

5.11.7 Decimation (Section 4.10.3): Proof of (4.278)

From (4.277) with M₁ = M₂ = M it follows that

(5.210)

In the rhs of (5.210), there are at most M (consecutive) values of h such that since when ranges in it results that . Therefore, (4.278) follows, accounting for the periodicity in with period 1 of .

5.11.8 Expansion and Decimation (Section 4.10.4): Proof of (4.286)

Accounting for (4.182) and (4.187) and using (4.285) and the sampling property of the Dirac delta, the cross-correlation function of x_I1(n) and x_D2(n) can be expressed as

(5.211)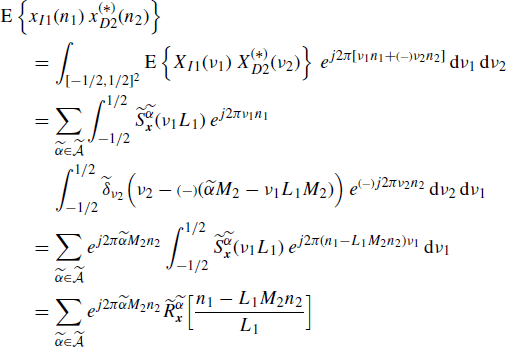

where, in the last equality, the Fourier-transform pair (4.244) and (4.245) is used. By substituting n₁ = n + m and n₂ = n we have (4.286).

5.11.9 Strictly Band-Limited SC Processes (Section 4.9.1): Proof of (4.287a)–(4.288b)

Let x₁(n) and x₂(n) be strictly band-limited processes with bandwidths B₁ and B₂, respectively. It results that

(5.212)

If x₁(n) and x₂(n) are jointly SC with Loève bifrequency cross-spectrum (4.190a), then (5.212) specializes into

(5.213)

Let us define the sets

(5.214)

(5.215)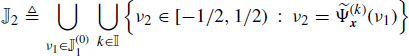

Analogously to the continuous-time case, without lack of generality the functions and in (4.190a) and (4.190b) can be chosen with supports such that the sets and are at most countable (Definition 4.2.4 and Theorem 4.2.7). In addition, let us assume that the number of cluster points (accumulation points) of and is at most finite. Thus, from (5.213) it follows that

(5.216)

where and , with cl{ · } denoting set closure. From (5.216) it follows that

(5.217)

almost everywhere for ν₁ [− 1/2, 1/2). However, since is at most countable, the cross-correlation (4.198a) is not modified assuming that (5.217) holds everywhere. Thus, (4.287a) and (4.287b) immediately follow.

Analogously, starting from (4.190b), the band-limitedness condition (5.212) leads to

(5.218)

from which (4.288a) and (4.288b) follow.

5.11.10 Interpolation Filters (Section 4.10.6): Proof of the Image-Free Sufficient Condition (4.290)

Accounting for (4.246a), (4.287a), and (4.287b), the support of each term in the sum over in (4.289) is given by

(5.219)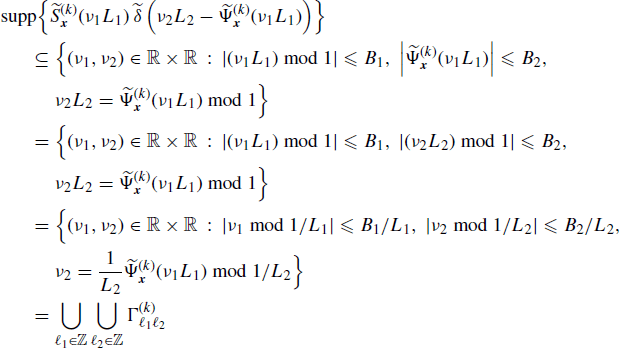

where

(5.220)

Let be the Fourier transform of . It results that

(5.221)

where

(5.222)

The following conditions are sufficient to assure that the Loève bifrequency cross-spectrum in (4.289) is a frequency-scaled image-free version of :

1. B_i ≤ 1/2, (i = 1, 2). So images do not overlap. That is, for every k and k′ in (possibly k = k′), one has

(5.223)

2. W_i ≤ 1/2, (i = 1, 2). So the filter passbands do not overlap. That is,

(5.224)

3. B_i/L_i ≤ W_i, (i = 1, 2). So the low-pass filters and capture the main images (( ₁, ₂) = (m₁L₁, m₂L₂), in (5.220)), i.e., those centered in . That is, one has

(5.225)

4. W_i ≤ 1/(2L_i), (i = 1, 2). So the low-pass filters and do not capture images different from the main ones. That is, one has

(5.226)

The sufficient conditions in items 1–4 can be summarized into the sufficient condition (4.290).

5.11.11 Interpolation Filters (Section 4.10.6): Proof of the Sufficient Conditions (4.291) and (4.292)

Let us assume that (4.290) holds. Thus the Loève bifrequency cross-spectrum in (4.289) is a frequency-scaled image-free version of with given by (4.246a)–(4.246c). In addition, form (4.290) and B₁ ≤ 1/2 it follows that

(5.227)

For a fixed , due to condition (4.291), it results that

(5.228)

If both conditions (5.227) and (5.228) are satisfied, then in expression (4.246b) of the Loève bifrequency cross-spectrum , for ν₁ [− 1/(2L₁), 1/(2L₁)] the support curve of the replica with h = 0 can intersect other support curves with the same k (h ≠ 0) only if on these other curves the spectral correlation density is zero. In fact, 1/L₁ − B₁/L₁ is the smallest |ν₁| in correspondence of which the image around ν₁ = ± 1/L₁ of the replica centered in ν₂ = 0 (h = 0 in (4.246b)) can have nonzero spectral correlation density. Moreover, 1/L₂ − B₂/L₂ is the smallest |ν₂| in correspondence of which the image around ν₁ = 0 of the replica centered in ν₂ = ± 1/L₂ (h = ± 1 in (4.246b)) can have nonzero spectral correlation density. Thus, the density of Loève bifrequency cross-spectrum (4.289) along the considered support curve is a frequency-scaled image-free version of the corresponding density of Loève bifrequency cross-spectrum ∀ν₁ [− 1/(2L₁), 1/(2L₁)].

Condition (5.228) holding for every jointly with B₂ ≤ 1/2 gives

(5.229)

(5.230)

which prove sufficiency of (4.291).

The proof of sufficiency of (4.292) is similar.

5.11.12 Decimation Filters (Section 4.10.7): Proof of the Aliasing-Free Sufficient Condition (4.293)

The Loève bifrequency cross-spectrum of x_D1(n) and x_D2(n) is given by (4.273a)–(4.273c). Accounting for (4.287a) and (4.287b), the support of each term in the sums over k, p₁, and p₂ in (4.273a) is given by

(5.231)

where

(5.232)

with p_i {0, 1, …, M_i − 1} and , (i = 1, 2).

If M_iB_i ≤ 1/2, (i = 1, 2), then

(5.233)

for every k and k′ in (possibly k = k′). Therefore, (4.293) is a sufficient condition to assure that the Loève bifrequency cross-spectrum is a frequency-scaled alias-free version of .

5.11.13 Decimation Filters (Section 4.10.7): Proof of the Sufficient Conditions (4.294) and (4.295)

Let us assume that condition (4.293) holds. Thus, the Loève bifrequency cross-spectrum in (4.273a)–(4.273c) is a frequency-scaled alias-free version of . From (4.293) it immediately follows that

(5.234)

For a fixed , due to condition (4.294) one obtains

(5.235)

If conditions (5.234) and (5.235) are both verified, then in expression (4.273b) of the Loève bifrequency cross-spectrum , for ν₁ [− 1/2, 1/2] the support curve of the replica with h = 0, p₁ = 0 can intersect other support curves with the same k (h ≠ 0, p₁ ≠ 0) only if on these other curves the spectral correlation density is zero. In fact, 1 − M₁B₁ is the smallest |ν₁| in correspondence of which replicas with p₁ = ± 1 can have nonzero spectral correlation density and 1 − M₂B₂ is the smallest |ν₂| in correspondence of which replicas with h = ± 1 can have nonzero spectral correlation density. Thus, the density of Loève bifrequency cross-spectrum (4.273b) along the considered support curve is a frequency-scaled alias-free version of the corresponding density of Loève bifrequency cross-spectrum for every ν₁ [− 1/2, 1/2].

Condition (5.235) holding for every jointly with B₂ ≤ 1/(2M₂) prove sufficiency of (4.294).

The proof of sufficiency of (4.295) is similar.

5.11.14 Fractional Sampling Rate Converters (Section 4.10.8): Proof of (4.296)

It results that

(5.236)

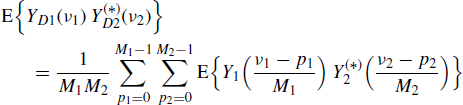
where, in the first and third equality, (4.272) and (4.245) are accounted for, respectively. By using (4.190a) into (5.236), (4.296) immediately follows.