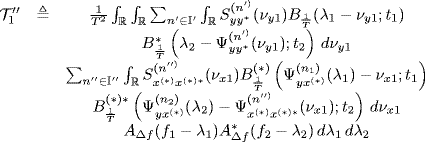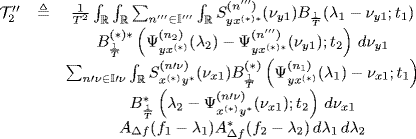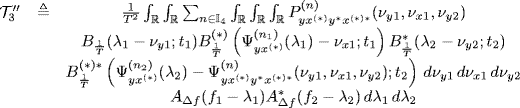4.6 The Frequency-Smoothed Cross-Periodogram
It is well known that the power spectrum of WSS processes can be consistently estimated by the frequency-smoothed periodogram, provided that some mixing assumptions regulating the memory of the process are satisfied (Parzen 1957), (Brillinger 1981), (Thomson 1982). Moreover, for ACS processes, the frequency-smoothed cyclic periodogram at a given cycle frequency is a mean-square consistent and asymptotically Normal estimator of the cyclic spectrum at that cycle frequency (Alekseev 1988), (Hurd 1989a), (Hurd 1991), (Hurd and Gerr 1991), (Hurd and Le
kow 1992a), (Dandawatacute; and Giannakis 1994), (Dehay and Hurd 1994), (Gerr and Allen 1994), (Dehay and Lekow 1996), (Sadler and Dandawatacute; 1998). In both cases of WSS and ACS processes, the frequency-smoothing procedure consists in considering frequency averages of the cross-periodogram along the support lines (with unity slope) of the Loève bifrequency spectrum. This technique was extended in (Allen and Hobbs 1992), (Lii and Rosenblatt 1998), and (Lii and Rosenblatt 2002) to the case of SC processes with known support lines with not necessarily unit slope.
By following the above idea, in this section the cross-periodogram frequency-smoothed along a known given support curve is proposed as estimator of the spectral correlation density on this support curve (Napolitano 2007c).
According to Definition 4.4.1, the bifrequency cross-periodogram of two stochastic processes 
and 
observed for t 
(− T/2, T/2) is defined as
Under Assumptions 4.4.3a and 4.4.5 (with Δf = 1/T), the expected value of the bifrequency cross-periodogram (4.146) is given in Lemma 4.4.6 (eq. (4.106) with Δf = 1/T). Under Assumptions 4.4.2a, 4.4.3a, and 4.4.5 (with Δf = 1/T), the covariance of the bifrequency cross-periodogram (4.146) is given in Lemma 4.4.7 (eq. (4.108) with Δf = 1/T). Under Assumptions 4.4.2a, 4.4.3a, 4.4.4, and 4.4.5 (with Δf = 1/T), the asymptotic (T→ ∞) expected value of the bifrequency cross-periodogram of two jointly SC processes is given in Theorem 4.4.8 (eq. (4.112) with Δf = 1/T). Finally, under Assumptions 4.4.2, 4.4.3, 4.4.4, and 4.4.5 (with Δf = 1/T), the asymptotic (T→ ∞) covariance of the bifrequency cross-periodogram of two zero-mean jointly SC processes is given in Theorem 4.4.9 (eq. (4.115) with Δf = 1/T). These results show that, as for WSS and ACS processes, the properly normalized cross-periodogram of SC processes is an asymptotically unbiased but not consistent estimator of the spectral correlation density function.
Definition 4.6.1 Given two jointly SC stochastic processes 
and 
, their frequency-smoothed cross-periodogram along the support curve 
is defined as
where AΔf(f1) is a Δf-bandwidth frequency-smoothing window and 
denotes convolution with respect to f1. 
Assumption 4.6.2 Frequency-Smoothing Window Regularity. AΔf(f) is a Δf-bandwidth frequency-smoothing window such that
with WA(f) a.e. continuous, 
, 
, and
By using the expressions of the expected value (Lemma 4.4.6) and covariance (Lemma 4.4.7) of the bifrequency cross-periodogram, the following results are obtained, where the made assumptions allow the interchange of the order of expectation, integral, and sum operations.
Theorem 4.6.3 Expected Value of the Frequency-Smoothed Cross-Periodogram. Let 
and 
be second-order harmonizable jointly SC stochastic processes with bifrequency cross-spectrum (4.15). Under Assumptions 4.4.3a (series regularity), 4.4.5 (data-tapering window regularity) (with Δf = 1/T), and 4.6.2 (frequency-smoothing window regularity), the expected value of the frequency-smoothed cross-periodogram (4.147) is given by
where
Proof: See Section 5.4.
The expected value of the frequency-smoothed cross-periodogram along a given support curve 
is influenced not only by 
, but also by the spectral cross-correlation densities 
relative to all the others support curves 
, m ≠ n, the influence being stronger from support curves 
closer to 
and with larger 
. Such a phenomenon is similar to the cyclic leakage phenomenon occurring in cyclic spectra estimates of ACS processes (Gardner 1986a), (Gardner 1987d) and the leakage phenomenon occurring in the estimation of cyclic statistics of GACS processes (Theorem 2.4.6), (Napolitano 2007a). Moreover, accounting for (4.151), in the sum over m in (4.150), all terms such that 
, give a significantly nonzero contribution. Thus, in correspondence of the at most countable set of values of f in which 
for n ≠ m, we have spikes in the spectral density estimate. In the special case of linear support curves, this behavior was observed in (Lii and Rosenblatt 2002).
Theorem 4.6.4 Covariance of the Frequency-Smoothed Cross-Periodogram. Let 
and 
be second-order harmonizable zero-mean singularly and jointly SC stochastic processes with bifrequency spectra and cross-spectra (4.95). Under Assumptions 4.4.2 (SC statistics), 4.4.3 (series regularity), 4.4.5 (data-tapering window regularity) (with Δf = 1/T), and 4.6.2 (frequency-smoothing window regularity) the covariance of the frequency-smoothed cross-periodogram (4.147) is given by
(4.152) 
where
Proof: See Section 5.4.