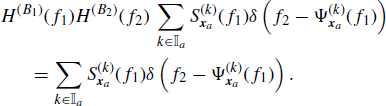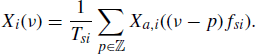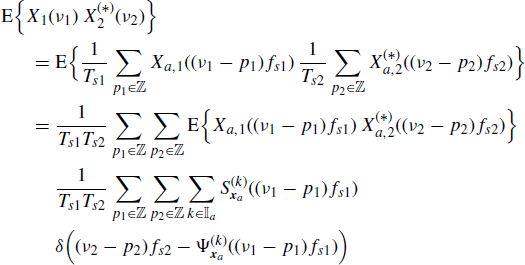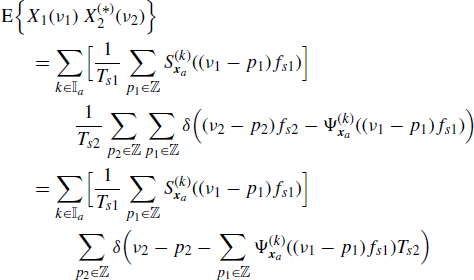5.10 Proofs for Section 4.9 “Sampling of SC Processes”

5.10.1 Proof of Theorem 4.9.2 Strictly Band-Limited Spectrally Correlated Processes

The strictly band-limitedness condition (4.204) considered in the frequency domain implies that

(5.179)

where . In the case of jointly SC processes, replacing (4.209a) into (5.179) leads to

(5.180)

Let

(5.181)

(5.182)

Without lack of generality, the functions and in (4.209a) and (4.209b) can be chosen such that both and are at most countable (Definition 4.2.4 and Theorem 4.2.7). Let us assume that the number of possible accumulation points (cluster points) of and is at most finite. Thus, from (5.180) it necessarily results that

(5.183)

where , with cl denoting set closure, represents the set of points f_i where there is no curve intersection (or accumulation points of such f_i). Consequently, condition in (4.210a) holds almost everywhere (a.e.). However, since is at most countable and with at most a finite number of accumulation points, the cross-correlation (4.24b) (with ) is not modified by assuming also for f₁ such that |f₁| > B₁ and . Therefore, we can assume that (4.210a) holds everywhere using suitable modifications of . Furthermore, from (5.180) it follows that for strictly band-limited SC processes the functions are undetermined for . Thus, for can be assumed in order to have these functions with compact support. The proof of (4.210b) is similar and, analogously, can be assumed for .

The proof of the converse is straightforward.

5.10.2 Proof of Theorem 4.9.4 Loève Bifrequency Spectrum of Sampled Jointly Spectrally Correlated Processes

The Fourier transform (4.185) of the sequence x_i(n) is linked to the Fourier transform (4.5) of the continuous-time signal x_a,i(t) by the relationship (Lathi 2002, Section 9.5)

(5.184)

Thus, accounting for (4.209a), one obtains

(5.185)

from which (4.213) follows by a scale change in the argument of the Dirac delta (Zemanian 1987, Section 1.7).

5.10.3 Proof of Theorem 4.9.5 Loève Bifrequency Spectrum of Sampled Strictly Band-Limited Jointly SC Processes

For strictly band-limited processes x_a,i(t), according to Corollary 4.9.3, the support of the replica with p₁ = p₂ = 0 in (4.213) is such that

(5.186)

Since the functions have compact support contained in [− B₁, B₁], are invertible, and have values in [− B₂, B₂] (Theorem 4.9.2), under the assumption f_si ≥ 2B_i, the result is that for every and there exists only one pair (ν₁, ν₂) [p₁ − 1/2, p₁ + 1/2) × [p₂ − 1/2, p₂ + 1/2) such that in the argument of the Dirac delta in the right-hand side of (5.185). Consequently, (5.185) can be written as

(5.187)

from which (4.190a) with (4.220a) and (4.221a) immediately follow. In addition, since replicas in (5.187) are separated by 1 in both variables ν₁ and ν₂ and the functions (of ν₁) and have compact support contained in [− B₁/f_s1, B₁/f_s1], condition f_s1 ≥ 2B₁ assures that replicas in (4.220a) and (4.221a) do not overlap.

The proof of (4.190b) with (4.220b) and (4.221b) is similar.

5.10.4 Proof of Theorem 4.9.6

Let us assume that f_si ≥ 2B_i, (i = 1, 2). Thus, according to Theorem 4.9.5, replicas in (5.187) do not overlap. However, mappings (4.222), (4.223) do not necessarily hold ∀ν₁ [− 1/2, 1/2].

From f_s1 ≥ 2B₁ it immediately follows that ∀ν₁ [− 1/2, 1/2]

(5.188)

Due to condition (4.226) for , it results that ∀ν₁ [− 1/2, 1/2]

(5.189)

Then in (5.187), for ν₁ [− 1/2, 1/2] the support curve of the replica with p₁ = p₂ = 0 can overlap support curves of other replicas (p₁ ≠ 0 and/or p₂ ≠ 0) only if on these other curves the spectral correlation density is zero. In fact, 1 − B₁/f_s1 [1 − B₂/f_s2] is the smallest |ν₁| [|ν₂|] such that replicas with p₁ = ± 1 [p₂ = ± 1] can have nonzero spectral correlation density. Thus conditions (4.222), (4.223) hold ∀ν₁ [− 1/2, 1/2]. (5.188) and (5.189) holding prove sufficiency of condition (4.226).

Analogous considerations lead to prove sufficiency of condition (4.227).