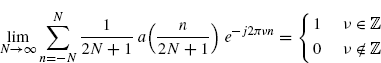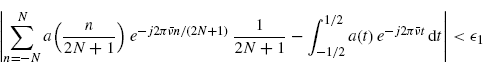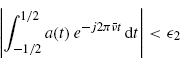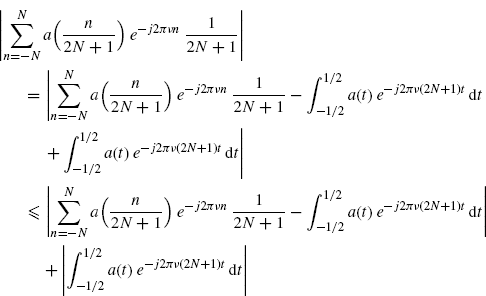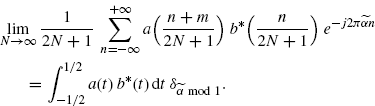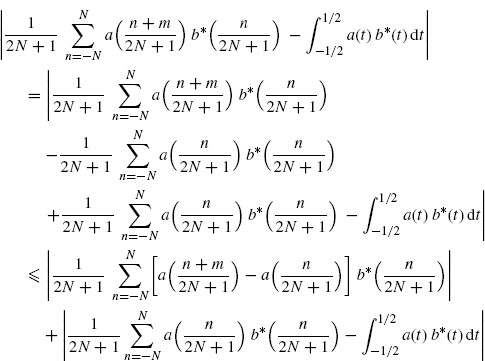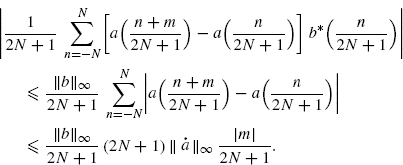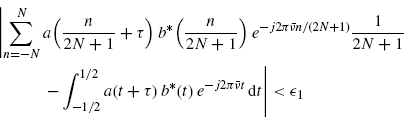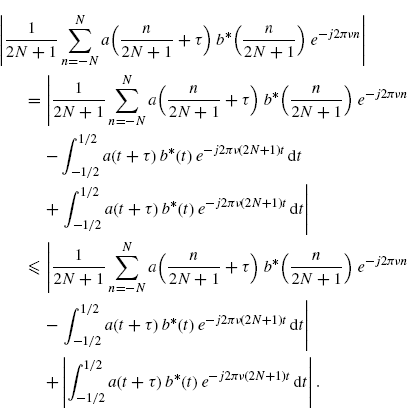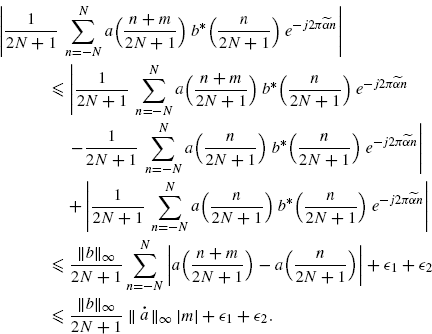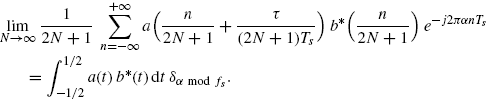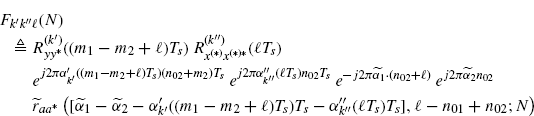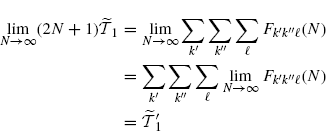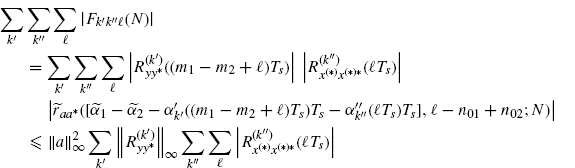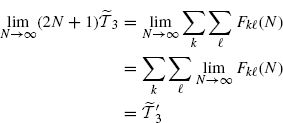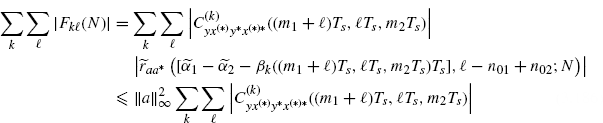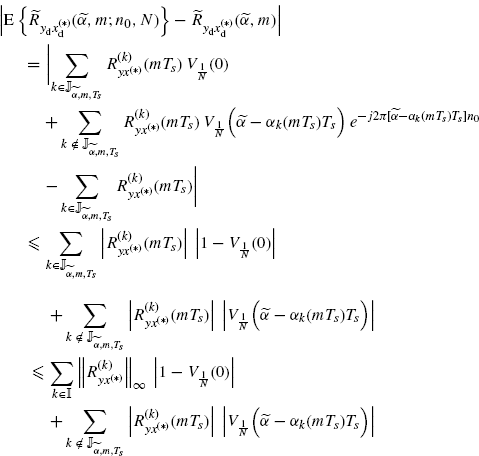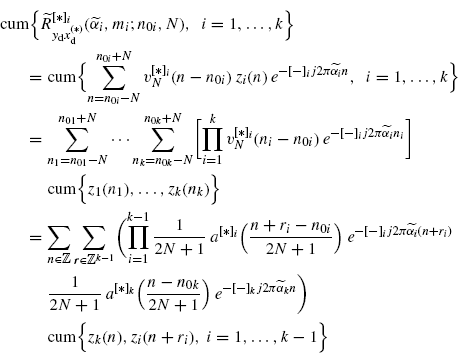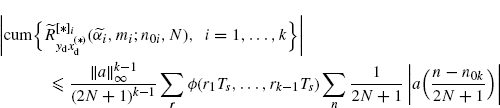3.10 Proofs for Section 2.6.2 “Asymptotic Results as N→ ∞”

Lemma 3.10.1 Let be given by (2.184) with a(t) as in Assumption 2.4.5. It results that

(3.155)

Proof: Since a(t) has finite support [− 1/2, 1/2), to prove (3.155) is equivalent to prove that

(3.156)

Let us consider first the case .

Since a(t) is Riemann integrable (Assumption 2.4.5), we have

(3.157)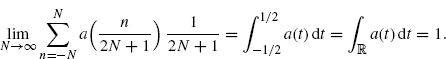

Let us consider now the case , ν > 0.

For every the function is Riemann integrable and we have

(3.158)

that is, ∀₁ > 0 such that for

(3.159)

(not necessarily uniformly with respect to ).

Since , the Riemann-Lebesgue theorem (Champeney 1990, Chapter 3) can be applied. Thus,

(3.160)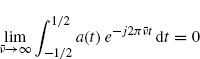

that is, ∀₂ > 0 such that for

(3.161)

Let us consider, now, the following inequality:

(3.162)

Since ν > 0, take ₂ arbitrarily small in (3.158), and define such that . Fix in (3.158) and take ₁ arbitrarily small and in (3.159). Let and . It results in in (3.161) and in (3.159). Thus, the right-hand side of (3.162) is bounded by ₁ + ₂ with ₁ and ₂ arbitrarily small, which proves (3.156) for ν > 0. Finally, note that the result holds for every non-integer ν since the function is periodic in ν with period 1.

As a final remark, note that Lemma 3.10.1 can also be obtained as corollary of the following Lemma 3.10.2 with b(t) = rect(t), m = 0. To prove Lemma 3.10.1, however, the assumption bounded is not used.

Lemma 3.10.2 Let a(t) be bounded and continuous in (− 1/2, 1/2) except, possibly, at t = ± 1/2, derivable almost-everywhere with bounded derivative, and let . Let both a(t) and b(t) be with finite support [− 1/2, 1/2], and such that for every τ [− 1, 1] the function a(t + τ)b^*(t) is Riemann integrable in [− 1/2, 1/2]. We have

(3.163)

Proof: The function b(t) has finite support [− 1/2, 1/2]. Thus the sum in (3.163) can be extended from −N to N.

. The following inequality holds

(3.164)

As regards the first term in the right-hand side of (3.164), observe that the first-order derivative exists a.e. and is bounded (Assumption 2.4.5). Therefore, for almost all t₁ and t₂ there exists such that and, hence, . Consequently,

(3.165)

As regards the second term in the right-hand side of (3.164), observe that the function a(t + τ)b^*(t) is Riemann integrable in [− 1/2, 1/2] so that, for τ = 0,

(3.166)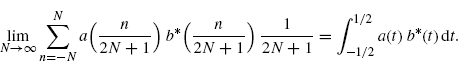

That is, ∀ > 0 ∃ N such that for N > N one has

(3.167)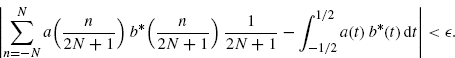

Therefore, the right-hand side of (3.164) is bounded by

which can be made arbitrarily small, provided that N is sufficiently large.

This proves (3.163) for .

. For every , , the function is Riemann integrable in [− 1/2, 1/2]. Thus

(3.168)

that is, ∀₁ > 0 such that for

(3.169)

not necessarily uniformly with respect to and τ. Since and , it results in . Thus, the Riemann-Lebesgue theorem (Champeney 1990, Section 3.7 can be applied:

(3.170)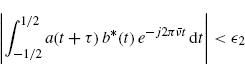

that is, ∀₂ > 0 such that for

(3.171)

not necessarily uniformly with respect to τ.

For arbitrarily small ₂, fix so that (3.171) holds. Once is fixed, for arbitrarily small ₁ fix such that (3.169) holds. Thus, by setting , in (3.169) and (3.171), we have the following inequality

(3.172)

Let such that . For , the right-hand side of (3.172) is bounded by ₁ + ₂ with ₁ and ₂ arbitrarily small. Thus, for ν ≠ 0 (and hence for ν non-integer due to the periodicity in ν) we have

(3.173)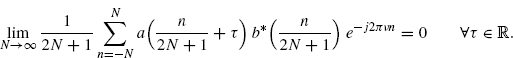

Accounting for (3.165) and (3.172) (with τ = 0), we have the following inequality.

(3.174)

The rhs of (3.174) can be made arbitrarily small. This proves (3.163) for .

This proof is simplified when a slightly modified version of this Lemma is used in Section 3.11 for the proof of the asymptotic covariance of the hybrid cyclic cross-correlogram. Specifically, we have the following.

(3.175)

3.10.1 Proof of Theorem 2.6.4 Asymptotic Expected Value of the Discrete-Time Cyclic Cross-Correlogram

From (2.183) it follows

(3.176)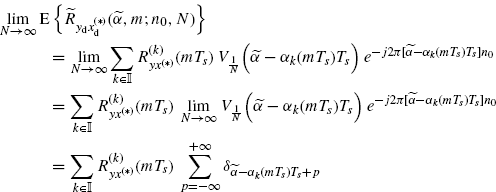

where, in the third equality, Lemma 3.10.1 is used.

In the second equality, the interchange of the limit and sum operations is justified by the Weierstrass criterium (Johnsonbaugh and Pfaffenberger 2002, Theorem 62.6; Smirnov 1964) since the series of functions of N

is uniformly convergent. In fact, by using (3.145) and Assumptions 2.4.3a and 2.4.5, we have

(3.177)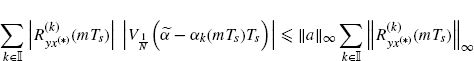

with the right-hand side bounded and independent of N.

3.10.2 Proof of Theorem 2.6.5 Asymptotic Covariance of the Discrete-Time Cyclic Cross-Correlogram

Let us consider the covariance expression (2.186). As regards the term defined in (2.187), let

It results that

(3.179)

where is defined in (2.196) and Lemma 3.10.2 (with a ≡ b) has been accounted for.

The interchange of the order of limit and sum operations in (3.179) is allowed since the three-index series over (k′, k^′′, ) of functions of N is uniformly convergent for the Weierstrass criterium (Johnsonbaugh and Pfaffenberger 2002, Theorem 62.6), (Smirnov 1964). In fact,

(3.180)

with the right-hand side independent of N, where the inequality

(3.181)

is used. The inequality in (3.181) follows from the fact that the sum over n is at most on 2N + 1 nonzero terms. The right-hand side of (3.180) is bounded due to Assumptions 2.4.3a and 2.4.8a. In particular, from Assumption 2.4.8a it follows that

(3.182)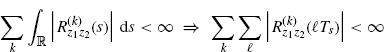

In fact, is the Riemann sum for the integral , with the function assumed to be Riemann integrable.

Analogously, it can be shown that

(3.183)

where is defined in (2.197).

As regards the term defined in (2.189), let

(3.184)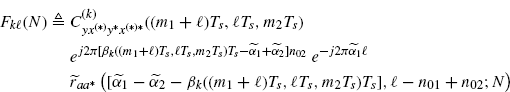

It results that

(3.185)

where is defined in (2.198) and Lemma 3.10.2 (with a ≡ b) has been accounted for.

The interchange of the order of limit and sum operations in (3.185) is allowed since the double-index series over k and of functions of N is uniformly convergent for the Weierstrass criterium (Johnsonbaugh and Pfaffenberger 2002, Theorem 62.6), (Smirnov 1964). In fact,

(3.186)

with the right-hand side independent of N, where the inequality (3.181) is used. The right-hand side of (3.186) is bounded due to Assumption 2.4.8b from which it follows that

(3.187)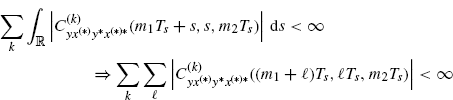

under the assumption that the function is Riemann integrable with respect to s.

As a final remark, observe that the sum over in (3.180) is finite. In fact, a(t) has finite support [− 1/2, 1/2] and, hence, only for −2N ≤ m ≤ 2N. Consequently, in (3.180), −2N ≤ − n₀₁ + n₀₂ ≤ 2N. This fact, however, is not sufficient to make the right-hand side of (3.180) independent of N. Therefore, Assumption 2.4.8a needs to be exploited.

Lemma 3.10.3 Let [− 1/2, 1/2], ≠ 0, and γ > 1. Thus

(3.188)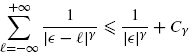

where .

Proof: For [− 1/2, 1/2], ≠ 0 one has

(3.189)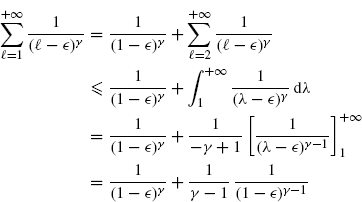

Thus,

(3.190)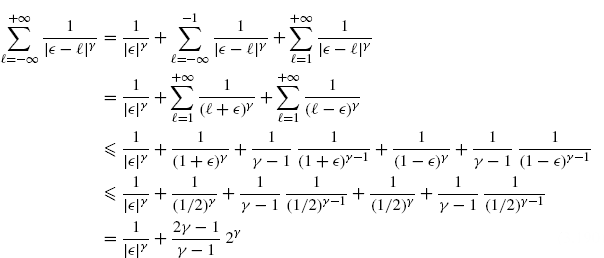

3.10.3 Proof of Theorem 2.6.7 Rate of Convergence of the Bias of the Discrete-Time Cyclic Cross-Correlogram

From (2.179b) and (2.200) it follows

(3.191)

and from (2.183) we have

Therefore,

(3.192)

Let us consider the first term in the rhs of (3.192). Accounting for (2.184) we have

(3.193)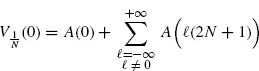

where A(f) is the Fourier transform of a(t) and A(0) = 1 (see (3.64)). According to Assumption 2.4.5, we have |A(f)| ≤ K/|f|^γ for |f| sufficiently large, say, |f| > f^*. Thus, for N sufficiently large such that 2N + 1 > f^* (and for | | 1), we have

(3.194)

where the sum in the third line is convergent when γ > 1. Note that in the special case of a rectangular data-tapering window a(t) = rect(t) ⇒ A(f) = sinc(f). Even if γ = 1, the result is that A( (2N + 1)) = 0 for ≠ 0, N integer. Thus, .

Let us now consider the second term in the rhs of (3.192).

From (2.184) we have

(3.195)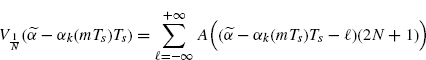

with never equal to zero since integer when . Moreover, under Assumption 2.6.6,

(3.196)

Let N be sufficiently large such that . Thus, for all and for all it results in and, hence,

(3.197)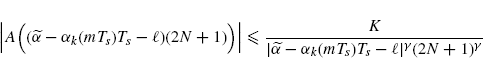

By taking in Lemma 3.10.3 (_k [− 1/2, 1/2), _k ≠ 0 for ), for every fixed , m, T_s, and k one obtains

(3.198)

Thus, by using (3.194)–(3.198) into (3.192), we have

(3.199)

where, in the last inequality, Assumption 2.6.6 () is used. Thus, (2.202) immediately follows.

For a rectangular lag-product-tapering window, , K_γ = 0 can be taken in (3.194), and (3.199) (with γ = 1) must be accordingly modified.

For a rectangular signal-tapering window, the corresponding lag-product-tapering window has Fourier transform such that (Fact 3.5.3)

(3.200)

Thus, (3.200) and (3.199) (with γ = 1) lead to

(3.201)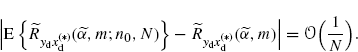

3.10.4 Proof of Lemma 2.6.9 Rate of Convergence to Zero of Cumulants of Discrete-Time Cyclic Cross-Correlograms

By using (2.181), (2.182), and the multilinearity property of cumulants we have

(3.202)

where, in the third equality, the variable changes n_k = n and n_i = n + r_i, i = 1, ..., k − 1 are made, r [r₁, ..., r_k−1], and all the sums are finite since the function a(·) has finite support (Assumption 2.4.5). Note that the order of finite sums can be freely interchanged. From (3.202) it follows that

(3.203)

where Assumption 2.6.8 is used and all the sums converge. In fact, ∑_rϕ(r₁T_s, ..., r_k−1T_s)T_s is the Riemann sum for and ∑_n|a((n − n_0k)/(2N + 1))|/(2N + 1) is the Riemann sum for . Thus, (2.206) immediately follows.

This lemma is the discrete-time counterpart of Lemma 2.4.17 on the rate of convergence to zero of the cumulant of continuous-time cyclic cross-correlograms. Note that in the discrete-time case Assumption 2.4.16 is not used. In fact, such assumption is used in the continuous-time case in Lemma 2.4.17 to interchange the order of integrals. In the discrete-time case, as a consequence of the finite support of a(·), all the sums are finite and their order can be freely interchanged.

3.10.5 Proof of Theorem 2.6.10 Asymptotic Joint Normality of the Discrete-Time Cyclic Cross-Correlograms

From Theorem 2.6.7 holding for γ > 1 (or γ = 1 if a(t) = rect(t)) we have

(3.204)

From Theorem 2.6.5 it follows that the asymptotic covariance

(3.205)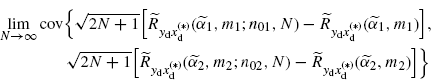

is finite. From Theorem 3.13.2 it follows that the asymptotic conjugate covariance is finite. Moreover, from Lemma 2.6.9 with and k 3 we have

(3.206)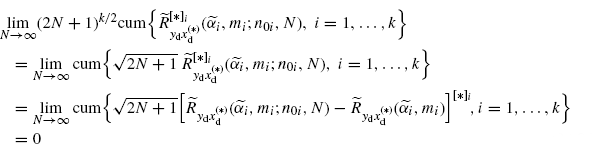

where the second equality holds since the value of the cumulant does not change by adding a constant to each of the random variables (Brillinger 1981, Theorem 2.3.1).

Thus, according to the results of Section 1.4.2, for every fixed the random variables , i = 1, ..., k, are asymptotically (N→ ∞) zero-mean jointly complex Normal (Picinbono 1996; van den Bos 1995).