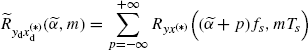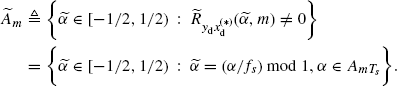2.5 Sampling of GACS Processes

In this section, the problem of uniformly sampling GACS processes is addressed. Aliasing formulas for second-order cyclic cross-moments are derived. It is shown that uniformly sampling a continuous-time GACS process leads to a discrete-time ACS process. Moreover, it is shown that continuous-time GACS processes do not have a discrete-time counterpart, that is, discrete-time GACS processes do not exist.

Let

(2.172)

be the discrete-time processes obtained by uniformly sampling with period T_s = 1/f_s the continuous-time (jointly) GACS processes x(t) and y(t).

Definition 2.5.1 The cyclic cross-correlation function of the discrete-time sequences y_d(n) and x_d(n) at cycle frequency is defined as

(2.173)

The magnitude and phase of are the amplitude and phase of the finite-strength additive complex sinewave component at frequency contained in the discrete-time cross-correlation .

Theorem 2.5.2 (Izzo and Napolitano 2003), (Napolitano 2009, Theorem 4.1). Uniformly sampling continuous-time jointly GACS processes leads to discrete-time jointly ACS processes.

Proof: Let be , with A_τ defined in (2.32a). Using (2.31b) and (2.31c) we have

(2.174a)

(2.174b)

(2.174c)

(2.174d)

where, (2.174d) is obtained observing that for every m the discrete-time almost-periodic function of n in (2.174c) can be expressed by a (generalized) Fourier series expansion with coefficients , defined in (2.173) and, moreover, let

(2.175)

the set

(2.176)

is countable. Then, the sum in (2.174d) can be extended either to or to . By substituting (2.174c) into (2.173) results in

(2.177)

In (2.177), mod b is the modulo b operation with values in [− b/2, b/2), that is,

(2.178)

with Mod b being the usual modulo b operation with values in [0, b). Thus, if and if .

From (2.174d) it follows that the cross-correlation function of the discrete-time processes y_d(n) and x_d(n) obtained by uniformly sampling two continuous-time jointly GACS processes y(t) and x(t) is a (discrete-time) almost-periodic function of n that can be expressed by a (generalized) Fourier series with cycle frequencies not depending on the lag parameter m. That is, y_d(n) and x_d(n) are jointly ACS.

The function is periodic in with period 1. It is linked to the cyclic cross-correlation function (2.33) and the generalized cyclic cross-correlation function (2.34)–(2.35) of the continuous-time signals y(t) and x(t) by the following result.

Theorem 2.5.3 Aliasing Formula for the Cyclic Cross-Correlation Function (Izzo and Napolitano 2003), (Napolitano 2009, Theorem 4.2). Let y_d(n) and x_d(n) be the discrete-time processes defined in (2.172). It results that

(2.179a)

(2.179b)

Proof: See Section 3.8.

Note that (2.179a) is the generalization to GACS signals of the analogous formula for ACS signals ((1.174) when y ≡ x).

In the following, consequences of Theorems 2.5.2 and 2.5.3 are analyzed. Furthermore, difficulties arising in cyclic spectral analysis of a continuous-time GACS process starting from the discrete-time process of its samples are discussed.

The set of cycle frequencies at lag m, accounting for (2.179a) can be expressed as

(2.180)

The set is countable and can contain cluster points (accumulation points) or be dense in [− 1/2, 1/2) if f_s is incommensurate with a countable infinity of cycle frequencies (e.g., if and ).

From (2.179a) it follows that, in general, due to the presence of aliasing in the cycle frequency domain. However, if the jointly GACS continuous-time signals y(t) and x(t) are such that at lag τ = mT_s there is no lag-dependent cycle frequency α_k(τ), , such that for p ≠ 0 then, by comparing (2.179b) with (2.39), it follows that . Such an equality could be difficult to be realized in the whole domain (Izzo and Napolitano 2003), as a consequence of the fact that GACS signals have the power spread over an infinite bandwidth (Sections 2.2.2 and 2.2.3), (Izzo and Napolitano 1998a, 2005). Furthermore, in Theorem 2.5.2, it is shown that the discrete-time signal constituted by the samples of a continuous-time GACS signal is a discrete-time ACS signal. Thus, discrete-time ACS signals can arise from sampling ACS and non-ACS continuous-time GACS signals. Moreover, in Section 2.7.6 it is shown that, starting from the sampled signal, the possible ACS or non-ACS nature of the continuous-time GACS signal can only be conjectured, provided that analysis parameters such as sampling period, padding factor, and data-record length are properly chosen. Thus, the results for discrete-time processes cannot be obtained straightforwardly from those of the continuous-time case as it can be made in the stationary case e.g., in (Brillinger and Rosenblatt 1967). In fact, unlike the case of WSS and ACS processes, continuous-time GACS processes do not have a discrete-time counterpart, that is, discrete-time GACS processes do not exist. This is a consequence of the fact that even if the set can be uncountable, the set is always countable.

From the above facts it follows that the sampling frequency f_s cannot be easily chosen in order to avoid or limit aliasing, as it happens for bandlimited WSS and ACS signals (Napolitano 1995), (Izzo and Napolitano 1996), even if, in some cases, as for the chirp-modulated signal (2.99), analytical results can be obtained (Section 2.7.1). However, in the following it will be shown that the discrete-time cyclic cross-correlogram of the sampled process can be made as close as desired to samples of the continuous-time cyclic cross-correlation function by taking the sampling period sufficiently small and the data-record length sufficiently large.