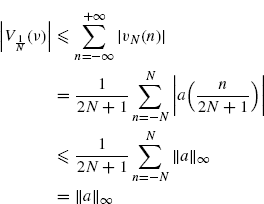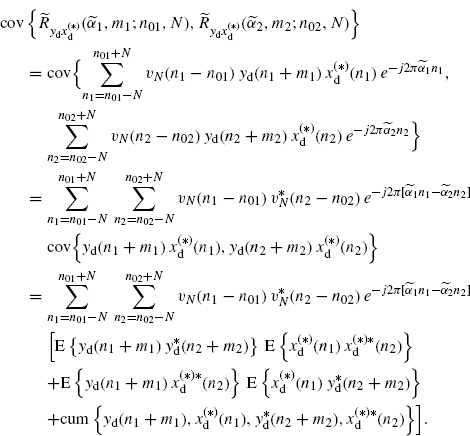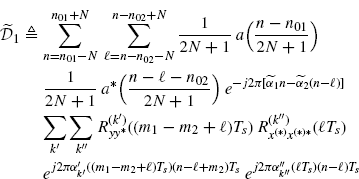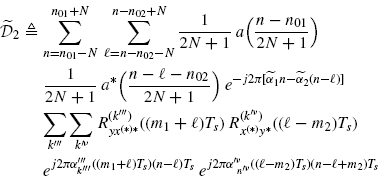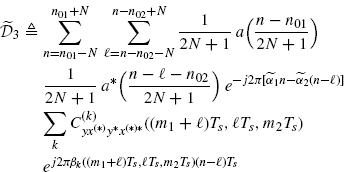3.9 Proofs for Section 2.6.1 “Discrete-Time Cyclic Cross-Correlogram”

3.9.1 Proof of Theorem 2.6.2 Expected Value of the Discrete-Time Cyclic Cross-Correlogram

By taking the expected value of both sides in (2.181) and using (2.174c) we get

(3.143)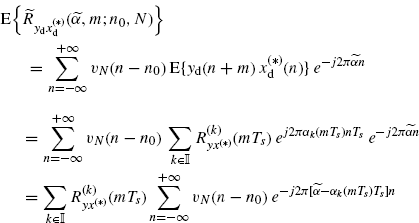

from which (2.183) immediately follows.

The data-tapering window is finite length (see (2.182)). Thus, in the first equality the sum over n is finite and can be freely interchanged with the expectation operator. In the second equality, Assumption 2.4.2a is used. In the third equality the order of the two sums can be interchanged since the double-index series over k and n is absolutely convergent (Johnsonbaugh and Pfaffenberger 2002, Theorem 29.4). In fact,

(3.144)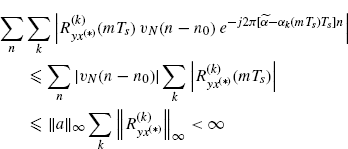

where Assumption 2.4.3a, (2.182), and the inequality (Assumption 2.4.5)

(3.145)

are used.

By substituting (2.182) into the first line of (2.184) we get

(3.146)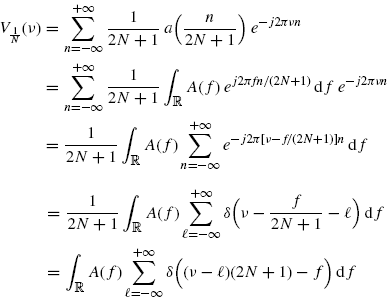

from which the right-hand side of (2.184) immediately follows. In (3.92), in the fourth equality the Poisson's sum formula (Zemanian 1987, p. 189)

(3.147)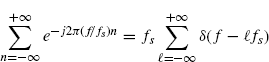

and in the fifth equality the scaling property of the Dirac delta δ(bt) = δ(t)/|b| (Zemanian 1987, p. 27) are used. Furthermore, equalities should be intended in the sense of distributions (generalized functions) (Zemanian 1987).

3.9.2 Proof of Theorem 2.6.3 Covariance of the Discrete-Time Cyclic Cross-Correlogram

For zero-mean stochastic processes, the covariance of the lag product can be expressed in terms of second-order moments and a fourth-order cumulant (see (3.45)). Then, using the multilinearity property of covariance, one obtains

(3.148)

By substituting (2.119) and (2.120) (Assumption 2.4.2) into (3.148), accounting for (2.182) and making the variable changes n₁ = n and n₂ = n− , it results in

(3.149)

where

(3.150)

(3.151)

(3.152)

In (3.150)–(3.152), for notation simplicity, , , , and . The sums over n and can be extended from −∞ to +∞, they remain the same finite sums due to the presence of the product of the two finite-length data-tapering windows a(·) and a^*(·). Then, by making the variable change n = n′+ n₀₂ + into (3.150)–(3.152) and using (2.190), (2.186)–(2.189) easily follow.

The interchange of covariance and sum operations in the second equality of (3.148) is allowed since the sums are finite (due to the finite support of ). The interchange of the order of sums to get (3.149)–(3.152) and then (2.186)–(2.189) is justified since the four-index series over (k′, k^′′, , n) in (3.150) and over (k^′′′, k ′ ν, , n) in (3.151) and the three-index series over (k, , n) in (3.152) are absolutely convergent (Johnsonbaugh and Pfaffenberger 2002, Theorem 29.4). In fact, as regards the term in (3.150), one has

(3.153)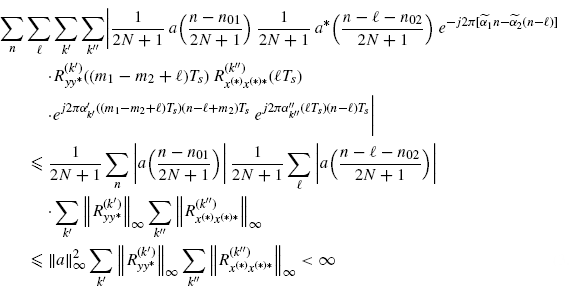

where the sums over n and are at most over 2N + 1 terms, and Assumptions 2.4.3a and 2.4.5 are used. The term in (3.151) can be treated analogously. As regards the term in (3.152), one has

(3.154)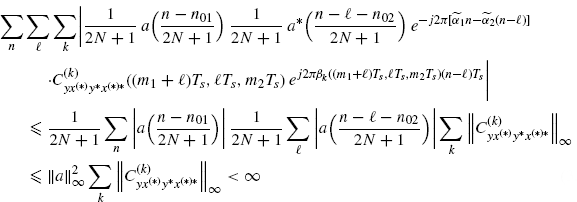

where Assumptions 2.4.3b and 2.4.5 are used.