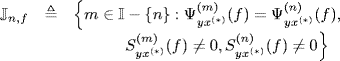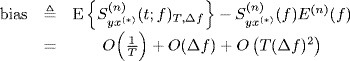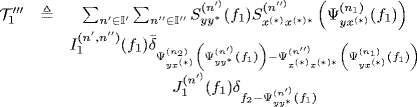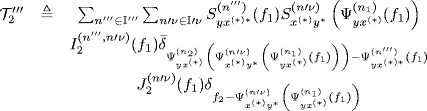4.7 Measurement of Spectral Correlation –Known Support Curves

In this section, for jointly SC processes the properly normalized frequency-smoothed cross-periodogram along a given support curve is considered as an estimator of the spectral cross-correlation density function on this support curve. Bias and covariance are determined. Moreover asymptotic unbiasedness, consistency, and asymptotic complex Normality are proved.

4.7.1 Mean-Square Consistency of the Frequency-Smoothed Cross-Periodogram

Assumption 4.7.1 Lack of Support-Curve Clusters (II). Let

(4.156)

be the set of indices of the curves , m ≠ n, that intercept in f.

There is no cluster of support curves. That is, for every and , the set is finite (or empty) and no curve with , can be arbitrarily close to the curve in f. That is, for every and

(4.157)

Assumption 4.7.1 is a slightly different formulation of the equivalent Assumption 4.5.3.

Assumption 4.7.2 Data-Tapering Window Regularity. The data-tapering window satisfies the regularity conditions of Assumption 4.4.5. In addition, the first-order derivative W_B exists a.e. and, where it exists, is uniformly bounded, , p = 1, 2, and there exists γ ≥ 1 such that W_B(f) = (|f|^−γ) as |f|→ ∞.

Assumption 4.7.3 Frequency-Smoothing Window Regularity. The frequency-smoothing window satisfies the regularity conditions of Assumption 4.6.2. In addition, , p = 1, 2.

Assumption 4.7.4 Spectral Cross-Correlation Density Regularity. The spectral cross-correlation density functions , , are a.e. derivable with uniformly bounded derivative.

Starting from the expressions of the expected value (Theorem 4.6.3) and covariance (Theorem 4.6.4) of the frequency-smoothed cross-periodogram, the following results are obtained, where the made assumptions allow the interchange of the order of sum, integral, and limit operations.

Theorem 4.7.5 Asymptotic Expected Value of the Frequency-Smoothed Cross-Periodogram. Let and be second-order harmonizable jointly SC stochastic processes with bifrequency cross-spectrum (4.15). Under Assumptions 4.4.3a (series regularity), 4.4.4 (support-curve regularity (I)), 4.4.5 (data-tapering window regularity) (with Δf = 1/T), and 4.8 (frequency-smoothing window regularity), the asymptotic (T→ ∞, Δf → 0, with TΔf→ ∞) expected value of the frequency-smoothed cross-periodogram (4.147) is given by

(4.158)

where

(4.159)

with denoting the first-order derivative of .

Proof: See Section 5.5.

From Theorem 4.7.5 it follows that the asymptotic expected value of the cross-periodogram frequency-smoothed along a known support curve is equal to the product of the spectral correlation density along the same curve and a multiplicative known bias term E⁽ⁿ⁾(f). Such a term does not depend on f if the support curve is a line (with any slope). In particular, it does not depend on f in the ACS case.

The contribution to the expected value of of spectral cross-correlation densities of support curves such that , m ≠ n, is present for finite T and Δf. It disappears in the limit as T→ ∞ and Δf → 0, provided that the order of these limits is not interchanged (TΔf→ ∞). In fact, for T→ ∞ and Δf fixed, the kernel K_T,Δf(f, ν ; n, m ; t) in (4.151) becomes smaller and smaller for m ≠ n, even if f = ν (see also (Lii and Rosenblatt 2002, Figure 3) for the case of support lines).

Theorem 4.7.6 Rate of Convergence of the Bias of the Frequency-Smoothed Cross-Periodogram. Let and be second-order harmonizable jointly SC stochastic processes with bifrequency cross-spectrum (4.15). Under Assumptions 4.2 a (series regularity), 4.3 (support-curve regularity (I)), 4.4 (data-tapering window regularity) (with Δf = 1/T), 4.7 (support-curve regularity (II)), 4.8 (frequency-smoothing window regularity), 4.9 (lack of support-curve clusters (II)), under the further regularity conditions on the data-tapering and frequency-smoothing windows Assumptions 4.10 and 4.11, and the spectral cross-correlation density regularity Assumption 4.12, asymptotically (T→ ∞, Δf → 0, with TΔf→ ∞) for every , that is, for all points f where two or more different curves do not intercept, one obtains

(4.160)

provided that T(Δf)² → 0.

Proof: See Section 5.5.

Theorem 4.7.7 Asymptotic Covariance of the Frequency-Smoothed Cross-Periodogram. Let and be second-order harmonizable zero-mean singularly and jointly SC stochastic processes with bifrequency spectra and cross-spectra (4.95). Under Assumptions 4.4.2 (SC statistics), 4.4.3 (series regularity), 4.4.4 (support-curve regularity (I)), 4.4.5 (data-tapering window regularity) (with Δf = 1/T), and 4.6.2 (frequency-smoothing window regularity), the asymptotic (T→ ∞, Δf → 0, with TΔf→ ∞) covariance of the frequency-smoothed cross-periodogram (4.147) is such that

(4.161)

where

(4.162)

(4.163)

with

(4.164)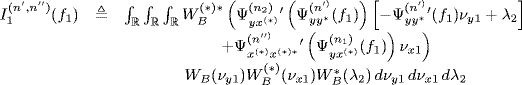

(4.165)

(4.166)

(4.167)

and if g(f) = 0 in a neighborhood of f and otherwise (then also if g(ν) = 0 for ν = f but g(ν) ≠ 0 for ν ≠ f).

Proof: See Section 5.5.

From Theorem 4.7.5 it follows that the frequency-smoothed cross-periodogram (smoothed along the known support curve ), normalized by E⁽ⁿ⁾(f), is an asymptotically unbiased estimator of the spectral cross-correlation density function along the same curve. Moreover, from Theorem 4.7.7 with n₁ = n₂, f₁ = f₂, and t₁ = t₂, it follows that the frequency-smoothed cross-periodogram has asymptotically vanishing variance of the order O((TΔf)⁻¹). Therefore, the properly normalized frequency-smoothed cross-periodogram is a mean-square consistent estimator of the spectral correlation density. That is,

(4.168)

In the special case of jointly ACS processes, the support curves , , , and are given by (4.118), (4.119), (4.120), and (4.118), respectively. By substituting these expressions and

into the asymptotic covariance expression (4.161), an expression equivalent, but for a multiplicative constant not depending on cycle and spectral frequencies, to the asymptotic covariance of the time-smoothed cyclic cross-periodogram (4.143) is obtained. In fact, in in (4.162) one has

(4.169)

(4.170)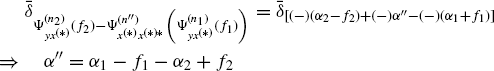

and in in (4.163) one has

(4.171)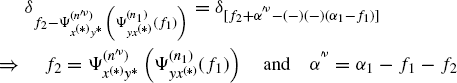

(4.172)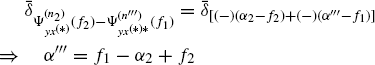

This result is in agreement with the asymptotic equivalence between time-and frequency-smoothed cyclic periodogram proved in (Gardner 1987d) for ACS signals.

4.7.2 Asymptotic Normality of the Frequency-Smoothed Cross-Periodogram

Assumption 4.7.8 Spectral Cumulants. For any choice of V_i, i = 1, . . . , k in {X, X^*, Y, Y^*}, V_i(f) are the (generalized) Fourier transforms of k processes kth-order jointly spectrally correlated (Section 4.2.3). That is,

(4.173)

with

(4.174)

where the cumulant of complex random variables is defined according to (Spooner and Gardner 1994) (see also (Napolitano 2007a) and Section 1.4.2).

Assumption 4.7.9 Derivatives of Support Functions. For every the support function is invertible. Both and its inverse are differentiable with uniformly bounded derivative.

In the stationary case the periodogram is distributed as and two periodograms are jointly (that is, are exponentially distributed) (Brillinger 1981, Theorem 5.2.6 p. 126) and the periodogram is asymptotically (T→ ∞) exponentially distributed.

In Section 1.4.2, it is shown that the Nth-order cumulant for complex random variables as defined in (Spooner and Gardner 1994, App. A) is zero for N ≥ 3 when the random variables are jointly complex Normal (Napolitano 2007a). This results is exploited in the following to prove the asymptotic complex Normality of the frequency-smoothed cross-periodogram.

Lemma 4.7.10 Cumulants of Frequency-Smoothed Cross-Periodograms. Let and be second-order harmonizable zero-mean singularly and jointly SC stochastic processes with bifrequency spectra and cross-spectra (4.95). Under Assumptions 4.4.5 (data-tapering window regularity), 4.6.2 (frequency-smoothing window regularity), 4.7.8 (spectral cumulants), 4.7.9 (derivatives of support functions), and assuming the spectral cross-correlation densities continuous a.e. (a weaker condition w.r.t. that in Assumption 4.12 (spectral cross-correlation density regularity)), for any k ≥ 2, one obtains

(4.175)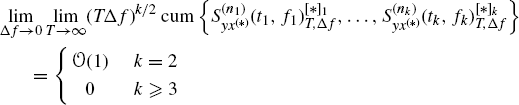

where [*]_i denotes ith optional complex conjugation and the order of the two limits cannot be interchanged (T→ ∞ and Δf → 0 with TΔf→ ∞).

Proof: See Section 5.6.

Theorem 4.7.11 Asymptotic Joint Complex Normality of the Frequency-Smoothed Cross-Periodograms. Under the assumptions for Theorem 4.7.6 (rate of convergence of the bias of the frequency-smoothed cross-periodogram) and Lemma 4.7.10 (cumulants of frequency-smoothed cross-periodograms), if Δf ≡ Δf_T = T^−a, with 3/5 < a < 1, it follows that for every fixed n_i, f_i, t_i the random variables

(4.176)

are asymptotically (T→ ∞ and Δf → 0 with TΔf→ ∞) zero-mean jointly complex Normal with asymptotic covariance matrix Σ with entries

(4.177)

given by (4.161) and asymptotic conjugate covariance matrix Σ^(c) with entries

(4.178)

given by (5.165).

Proof: See Section 5.6.

Corollary 4.7.12 Asymptotic Complex Normality of the Frequency-Smoothed Cross-Periodogram. Under the assumptions of Theorem 4.7.11, it follows that for every fixed n, f, t, the random variable is asymptotically zero-mean complex Normal:

(4.179)

as T→ ∞ and Δf → 0 with TΔf→ ∞.

From the asymptotic Normality and the expression of the asymptotic covariance of the frequency-smoothed cross-periodogram, it follows the asymptotic independence of the frequency-smoothed cross-periodograms for frequencies separated of at least Δf.

4.7.3 Final Remarks

In this section, some remarks are made on the results of Sections 4.5, 4.7.1, and 4.7.2. Specifically, it is shown how some assumptions made to obtain results of Sections 4.5, 4.7.1, and 4.7.2 can be relaxed or modified.

• In the asymptotic results of Theorems 4.7.13 and 4.7.15, we have that T→ ∞ and Δf → 0, in this order, so that TΔf→ ∞. Therefore, we can take Δf finite and fixed, make T→ ∞, and then make Δf → 0. Analogously, we could consider Δf = Δf_T such that Δf_T → 0 and TΔf_T→ ∞ as T→ ∞. This approach is adopted in Theorem 4.7.16 and in (Dandawatacute; and Giannakis 1994) and (Sadler and Dandawatacute; 1998) for ACS processes.
• In general, a rectangular data-tapering window cannot be used in the previous results since it does not satisfy Assumption 4.4. In fact,

• The proofs of the Theorems of Sections 4.4 –4.7.1 can be carried out with minor changes by substituting Assumption 4.2 with the following one.

Assumption 4.7.13 Spectral-Density Summability.

a. For any choice of z₁ and z₂ in {x, x^*, y, y^*}, the functions in (4.95) are almost everywhere (a.e.) continuous and such that

(4.180)

b. The functions in (4.96) are a.e. continuous and such that

(4.181)

Assumption 4.7.13a is similar to Assumption A1 in (Lii and Rosenblatt 2002), where, however, only a finite set of support curves (lines) are considered.

If Assumption 4.7.13 is made instead of Assumption 4.2, then several bounds derived in the proofs of Theorems of Sections 4.4 –4.7.1 (see Sections 5.2 – 5.5) should be modified as shown in Section 5.7. In this case, W_B(f) does not need to be summable and we can take (i.e., ).

• If there is no cluster of support curves (Assumption 4.6) and W_B(f) and W_A(f) are both rigorously band-limited, then all the sums in (4.150), (4.153), (4.154), and (4.155) reduce to finite sums.

In fact, let Λ₁ = λ₁ or , and Λ₂ = λ₂ or , and let or or or . In the case of W_B rigorously bandlimited, in the arguments of the integrals in (4.150), (4.153), (4.154), and (4.155) there are products of the kind

with ν integration variable.

For fixed Λ₁ and Λ₂, each product is nonzero only in correspondence of a finite number of values of n since ν (Λ₁ − 1/(2T), Λ₁ + 1/(2T)) due to the presence of the second rect. This result is still valid if Λ₁ and Λ₂ range in a finite interval of values, that is, if also W_A is rigorously bandlimited.

Thus, Assumption 4.4.3 can be relaxed. Specifically, (4.97) and (4.98) are not necessary. This situation occurs in the simulation experiment in Section 4.12.2 and in (Napolitano 2003, Section V), where the Fourier transform B_Δf of the data-tapering window is rectangular and, for the PAM signal with full duty-cycle rectangular pulse, (4.97) (or (Napolitano 2003, eq. (36))) is not satisfied.