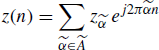1.2 Almost-Periodic Functions
In this section, definitions and main results on almost-periodic (AP) functions and their generalizations are presented for both continuous-and discrete-time cases. For extensive treatments on almost-periodic functions, see (Besicovitch 1932), (Bohr 1933), and (Corduneanu 1989) for continuous-time, and (Corduneanu 1989, Chapter VII), (Jessen and Tornehave 1945), and (von Neumann 1934) for discrete-time.
1.2.1 Uniformly Almost-Periodic Functions
Definition 1.2.1 (Besicovitch 1932, Chapter 1). A function z(t), ![]() , is said to be uniformly almost-periodic if
, is said to be uniformly almost-periodic if ![]() such that for any interval
such that for any interval ![]() such that
such that
(1.51) ![]()
The quantity ![]() is said translation number of z(t) corresponding to
is said translation number of z(t) corresponding to ![]() .
. ![]()
A set ![]() is said to be relatively dense in
is said to be relatively dense in ![]() if
if ![]() such that
such that ![]() the result is that D∩ I ≠ .
the result is that D∩ I ≠ .
Thus, defined the set of the translation numbers of z(t) corresponding to ![]()
(1.52) ![]()
according to Definition 1.2.1, the function z(t) is uniformly almost periodic if and only if ![]() the set
the set ![]() is relatively dense in
is relatively dense in ![]() . That is, there are many translation numbers of z(t) corresponding to
. That is, there are many translation numbers of z(t) corresponding to ![]() .
.
Theorem 1.2.2 (Besicovitch 1932, Chapter 1). Any uniformly AP function is the limit of a uniformly convergent sequence of trigonometric polynomials in t (generalized Fourier series):
where the frequencies α ![]() A, with A countable set of possibly incommensurate reals and possibly containing cluster points, and
A, with A countable set of possibly incommensurate reals and possibly containing cluster points, and
with the limit independent of t0. Thus, z(t) is bounded and uniformly continuous. ![]()
Theorem 1.2.3 (Besicovitch 1932, Chapter 1). For any uniformly AP function the following Parseval's equality holds
(1.55) ![]()
![]()
A function z(t) is periodic with period T0 > 0 if T0 is the smallest nonzero value such that
(1.56) ![]()
Thus, periodic functions are obtained as special case of almost-periodic functions with ![]() independent of
independent of ![]() ,
, ![]() . In such a case, the frequencies of the set A are all multiple of a fundamental frequency 1/T0, that is,
. In such a case, the frequencies of the set A are all multiple of a fundamental frequency 1/T0, that is, ![]() and (1.53) is the ordinary Fourier series expansion of the periodic function z(t).
and (1.53) is the ordinary Fourier series expansion of the periodic function z(t).
An example of uniformly AP function which is not periodic is
(1.57) ![]()
Both cosines are periodic functions with periods T0 and ![]() , respectively. However, their sum is not periodic since the ratio of the two periods T0 and
, respectively. However, their sum is not periodic since the ratio of the two periods T0 and ![]() is the irrational number
is the irrational number ![]() .
.
The functions defined in Definition 1.2.1 and characterized in Theorem 1.2.1 are called almost-periodic in the sense of Bohr (Bohr 1933, paragraphs 84–92) or, equivalently, uniformly almost periodic in the sense of Besicovitch (Besicovitch 1932, Chapter 1), or, equivalently, almost-periodic with respect to the sup norm. More general classes of almost-periodic functions, including possibly discontinuous functions, are treated in (Besicovitch 1932, Chapter 2) and the following sections.
1.2.2 AP Functions in the Sense of Stepanov, Weyl, and Besicovitch
The almost-periodicity property can be defined with respect to the following norms or seminorms, with p ≥ 1, (Besicovitch 1932, Chapter 2):
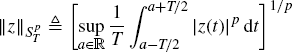
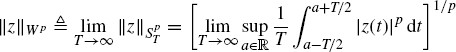
(1.60) 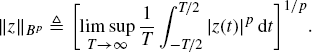
Functions belonging to ![]() with finite Besicovitch Bp-seminorm form a seminormed space called Marcinkiewicz space
with finite Besicovitch Bp-seminorm form a seminormed space called Marcinkiewicz space ![]() .
.
Let ![]() denote any of the above defined (semi)norms, that is,
denote any of the above defined (semi)norms, that is, ![]() ,
, ![]() , or
, or ![]() . For each (semi)norm, a definition of almost-periodicity can be given.
. For each (semi)norm, a definition of almost-periodicity can be given.
Definition 1.2.4 ![]() , Wp, and Bp Almost Periodicity (Besicovitch (1932) Chapter 2). A function z(t) is said to be Gp almost-periodic (Gp-AP), p ≥ 1, if ∀
, Wp, and Bp Almost Periodicity (Besicovitch (1932) Chapter 2). A function z(t) is said to be Gp almost-periodic (Gp-AP), p ≥ 1, if ∀![]() > 0 ∃
> 0 ∃ ![]()
![]() > 0 such that for any interval
> 0 such that for any interval ![]() such that
such that
(1.61) ![]()
Specifically, if ![]() , then z(t) is said
, then z(t) is said ![]() -AP; If
-AP; If ![]() , then z(t) is said
, then z(t) is said ![]() ; If
; If ![]() , then z(t) is said
, then z(t) is said ![]() -AP.
-AP. ![]()
Theorem 1.2.5 (Besicovitch 1932, Chapter 2). Any Gp-AP function is Gp-bounded (![]() ) and is the Gp-limit of a sequence of trigonometric polynomials in t:
) and is the Gp-limit of a sequence of trigonometric polynomials in t:
where An is an increasing sequence of countable sets such that ![]() and
and ![]() . The coefficients zα of the generalized Fourier series are given by (1.54).
. The coefficients zα of the generalized Fourier series are given by (1.54). ![]()
In (Besicovitch 1932, p. 74) it is shown that: If ![]() , then z1(t) = z2(t) a.e.; If
, then z1(t) = z2(t) a.e.; If ![]() , then z1(t) and z2(t) may differ at a set of points of finite and even of infinite measure. In addition, for p ≥ 1 the result is that (Besicovitch 1932, p. 73)
, then z1(t) and z2(t) may differ at a set of points of finite and even of infinite measure. In addition, for p ≥ 1 the result is that (Besicovitch 1932, p. 73) ![]() .
.
Theorem 1.2.6 (Besicovitch 1932, Chapter 2). For any G2-AP function the following Parseval's equality holds
(1.63) ![]()
![]()
Further generalizations of almost-periodic functions can be found in (Besicovitch 1932, Chapter 2), (Bohr 1933, paragraphs 94–102), and (Corduneanu 1989, Chapter VI).
1.2.3 Weakly AP Functions in the Sense of Eberlein
Definition 1.2.7 Weakly Almost-Periodic Functions (Eberlein 1949, 1956). A continuous and bounded function z(t) is said to be weakly almost-periodic (w.a.p.) (in the sense of Eberlein) if the set of translates z(t + τ), ![]() , is (conditionally) weakly compact in the set of continuous and bounded functions
, is (conditionally) weakly compact in the set of continuous and bounded functions ![]() .
. ![]()
Examples of w.a.p. functions are the uniformly almost periodic functions (in the sense of Definition 1.2.1), the positive definite functions (hence Fourier-Stieltjes transforms), and functions vanishing at infinity (Eberlein 1949, Theorems 11.1 and 11.2). A w.a.p. function is uniformly continuous (Eberlein 1949, Theorem 13.1).
Theorem 1.2.8 (Eberlein 1956). Every w.a.p. function z(t) admits a unique decomposition
(1.64) ![]()
where zuap(t) is a uniformly almost-periodic function in the sense of Definition 1.2.1 and z0(t) is a zero-power function
Moreover, it results that
(1.66a) 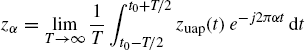
(1.66b) 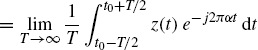
and, accordingly with (1.65) and using the notation of Theorem 1.2.5, the result is that
(1.67) ![]()
![]()
Theorem 1.2.9 (Eberlein 1956). For any w.a.p. function the following Parseval's equality holds
(1.68) ![]()
![]()
It is worthwhile emphasizing that the set of w.a.p. functions, unlike other classes of generalized AP functions, is closed under multiplication (Eberlein 1949). That is, the product of two w.a.p. functions is in turn a w.a.p. function.
Other definitions of w.a.p. functions different from Definition 1.2.7 are given in (Amerio and Prouse 1971, Chapter 3), (Corduneanu 1989, Section VI.5), (Zhang and Liu 2010).
Theorem 1.2.10 (Eberlein 1949, Theorem 15.1). Let z1(t) and z2(t) be w.a.p. functions. Then
(1.69) ![]()
exists and is a uniformly almost periodic function of t. A similar result also holds with different definitions of w.a.p. functions (Zhang and Liu 2010). ![]()
1.2.4 Pseudo AP Functions
Definition 1.2.11 (Ait Dads and Arino 1996). The function z(t) is said to be pseudo almost-periodic in the sense of Ait Dads and Arino, shortly ![]() , if it admits the (unique) decomposition
, if it admits the (unique) decomposition
(1.70) ![]()
where zuap(t) is a uniformly almost-periodic function in the sense of Definition 1.2.1 and z0(t), referred to as the ergodic perturbation, is a Lebesgue measurable function such that
(1.71) ![]()
shortly ![]() .
. ![]()
The classes ![]() and
and ![]() are slight generalizations of the classes
are slight generalizations of the classes ![]() and
and ![]() , respectively, of the pseudo almost-periodic functions in the sense of Zhang (Zhang 1994, 1995), where z(t) and z0(t) are assumed to be continuous and bounded.
, respectively, of the pseudo almost-periodic functions in the sense of Zhang (Zhang 1994, 1995), where z(t) and z0(t) are assumed to be continuous and bounded.
Theorem 1.2.12 (Ait Dads and Arino 1996). Let be ![]() . It results that
. It results that
(1.72a) 
(1.72b) 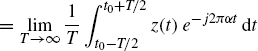
![]()
Proposition 1.2.13 (Ait Dads and Arino 1996). If ![]() exists, then
exists, then ![]() 0 and z(t) belong to the class of the asymptotically almost-periodic functions in the sense of Frechet.
0 and z(t) belong to the class of the asymptotically almost-periodic functions in the sense of Frechet.
Properties of asymptotically almost-periodic functions are given in (Le![]() kow and Napolitano 2006, Section 6.2).
kow and Napolitano 2006, Section 6.2).
1.2.5 AP Functions in the Sense of Hartman and Ryll-Nardzewski
Definition 1.2.14 (Kahane 1962), (Andreas et al. (2006) Definition 7.1). The function ![]() is said to be almost periodic in the sense of Hartman, shortly
is said to be almost periodic in the sense of Hartman, shortly ![]() , if,
, if, ![]()
exists and is finite. ![]()
Definition 1.2.15 (Kahane 1962), (Andreas et al. (2006) Definition 7.2). The function ![]() is said to be almost periodic in the sense of Ryll-Nardzewski, shortly
is said to be almost periodic in the sense of Ryll-Nardzewski, shortly ![]() , if,
, if, ![]()
exists uniformly with respect to ![]() and is finite.
and is finite. ![]()
Obviously, if ![]() , then
, then ![]() and
and ![]() , but the converse is not true. That is,
, but the converse is not true. That is, ![]() .
.
If ![]() or
or ![]() , then
, then ![]() and the Fourier coefficients of the (generalized) Fourier series in (1.62) are coincident with those in (1.74). If
and the Fourier coefficients of the (generalized) Fourier series in (1.62) are coincident with those in (1.74). If ![]() , then
, then ![]() (but not necessarily
(but not necessarily ![]() ) and the Fourier coefficients of the (generalized) Fourier series in (1.62) are (obviously) those in (1.73).
) and the Fourier coefficients of the (generalized) Fourier series in (1.62) are (obviously) those in (1.73).
Theorem 1.2.16 (Kahane 1961), (Andreas et al. (2006) Theorem 7.5). The spectrum of ![]() , that is the set
, that is the set ![]() , is at most countable. Consequently, also the spectrum of
, is at most countable. Consequently, also the spectrum of ![]() is at most countable.
is at most countable. ![]()
Theorem 1.2.17 (Urbanik 1962), (Kahane 1961). Let ![]() , p > 1. Then, the following unique decomposition holds
, p > 1. Then, the following unique decomposition holds
where zBap(t) is a Bp-AP function and ![]() with empty spectrum, that is
with empty spectrum, that is ![]()
(1.76) ![]()
![]()
In particular, since uniformly AP functions in the sense of Definition 1.2.1 are special cases of Bp-AP functions, the function zBap(t) in decomposition (1.75) can reduce to a uniformly AP function.
Let us define the sets
(1.77) ![]()
(1.78) ![]()
Obviously R0 ⊂ H0.
Theorem 1.2.18 (Kahane 1962). Let be ![]() . Then, there exists
. Then, there exists ![]()
![]() such that
such that ![]() . Let be
. Let be ![]() . Then, there exists
. Then, there exists ![]() such that
such that ![]() .
. ![]()
Theorem 1.2.19 (Kahane 1962). Let be ![]() . Then, there exist
. Then, there exist ![]() such that
such that ![]() .
. ![]()
Theorem 1.2.20 (Kahane 1962). Let x(t) be uniformly continuous and bounded. Then, there exist ![]() uniformly continuous and bounded such that
uniformly continuous and bounded such that ![]() . In particular, x(t) can be uniformly almost periodic.
. In particular, x(t) can be uniformly almost periodic. ![]()
1.2.6 AP Functions Defined on Groups and with Values in Banach and Hilbert Spaces
Almost-periodic functions and their generalizations on groups are treated in (Corduneanu 1989, Chapter VII), (von Neumann 1934), (Casinovi 2009).
Almost-periodic functions with values in Hilbert spaces are treated in (Phong 2007). Further classes of AP functions with values in Banach spaces and a survey of their properties are presented in (Andreas et al. 2006), (Chérif 2011a,b).
1.2.7 AP Functions in Probability
Let ![]() , denoted shortly by z(t), be a random process defined on a probability space
, denoted shortly by z(t), be a random process defined on a probability space ![]() .
.
Definition 1.2.21 Random Functions Almost-Periodic in Probability (Corduneanu (1989) Sect. II.3). A random process z(t), ![]() , is called almost-periodic in probability if
, is called almost-periodic in probability if ![]() ,
, ![]() , there exists
, there exists ![]() such that for every set of length
such that for every set of length ![]() , say
, say ![]() , there exists at least one number
, there exists at least one number ![]() such that
such that
(1.79) ![]()
The real number ![]() is said
is said ![]() -almost period in probability.
-almost period in probability. ![]()
Theorem 1.2.22 (Corduneanu 1989, Sect. II.3). Any random process AP in probability is bounded in probability and is the limit in probability of a sequence of random trigonometric polynomials in t. That is, ∀η > 0,
(1.80) ![]()
where An is an increasing sequence of countable sets of real numbers α and zα(ω) are random variables.
1.2.8 AP Sequences
Definition 1.2.23 Discrete-Time Almost-Periodic Functions (Corduneanu 1989, Chapter VII), (Jessen and Tornehave 1945), (von Neumann 1934). A sequence z(n), ![]() , is said to be almost-periodic if
, is said to be almost-periodic if ![]() such that for any set
such that for any set ![]()
![]() such that
such that
(1.81) ![]()
The integer m![]() is said to be the translation number of z(n) corresponding to
is said to be the translation number of z(n) corresponding to ![]() .
. ![]()
Theorem 1.2.24 (Corduneanu 1989, Chapter VII), (von Neumann 1934). Every AP sequence ![]() is the limit of a sequence of trigonometric polynomials in n:
is the limit of a sequence of trigonometric polynomials in n:
where the frequencies ![]() , with
, with ![]() countable set with possibly incommensurate elements in [− 1/2, 1/2) and possibly containing cluster points,
countable set with possibly incommensurate elements in [− 1/2, 1/2) and possibly containing cluster points,
(1.83) 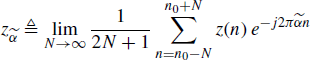
with the limit independent of n0 and
(1.84) ![]()
Thus, z(n) is bounded. ![]()
A sequence z(n) is periodic with period N0 if N0 is the smallest non-zero integer such that
(1.85) ![]()
Thus, periodic sequences are obtained as a special case of almost-periodic sequences with m![]() = kN0 independent of
= kN0 independent of ![]() ,
, ![]() . In such a case,
. In such a case, ![]() is the finite set {0, 1/N0, ..., (N0 − 1)/N0} or any equivalent set k0 + A
is the finite set {0, 1/N0, ..., (N0 − 1)/N0} or any equivalent set k0 + A ![]() {k0, k0 + 1/N0, ..., k0 + (N0 − 1)/N0} with k0 integer, and (1.82) is the discrete Fourier series (DFS) of z(n).
{k0, k0 + 1/N0, ..., k0 + (N0 − 1)/N0} with k0 integer, and (1.82) is the discrete Fourier series (DFS) of z(n).
In continuous-time, the complex sinewave ![]() is periodic with period
is periodic with period ![]() and the polynomial phase signal
and the polynomial phase signal ![]() , γ > 1, is not almost periodic. Complex discrete-time sinewaves and polynomial phase sequences require more attention. The sequence
, γ > 1, is not almost periodic. Complex discrete-time sinewaves and polynomial phase sequences require more attention. The sequence ![]() with
with ![]() , p, q relative prime integers or co-prime (that is, they have no common positive divisor other than 1 or, equivalently, their greatest common divisor is 1 or, equivalently, p/q is an irreducible fraction), is periodic with period q. In contrast, the sequence
, p, q relative prime integers or co-prime (that is, they have no common positive divisor other than 1 or, equivalently, their greatest common divisor is 1 or, equivalently, p/q is an irreducible fraction), is periodic with period q. In contrast, the sequence ![]() with
with ![]() , is almost periodic (not periodic). For every positive integer L ≥ 2, the sequence
, is almost periodic (not periodic). For every positive integer L ≥ 2, the sequence ![]() with
with ![]() , p, q relative prime integers, is periodic with period q whereas it is not almost periodic for
, p, q relative prime integers, is periodic with period q whereas it is not almost periodic for ![]() .
.
1.2.9 AP Sequences in Probability
Definition 1.2.25 Almost-Periodic Random Sequences in Probability (Han and Hong 2007). A random sequence z(n), ![]() , is called almost-periodic in probability if
, is called almost-periodic in probability if ![]() ,
, ![]() , there exists
, there exists ![]() such that for every set of length
such that for every set of length ![]() , say
, say ![]() , there exists at least one number
, there exists at least one number ![]() such that
such that
(1.86) ![]()
The integer m![]() ,η is said to be (
,η is said to be (![]() , η)-almost period in probability.
, η)-almost period in probability.