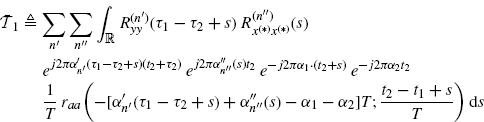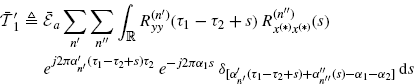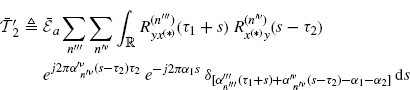3.7 Conjugate Covariance

For complex-valued processes, both covariance and conjugate covariance are needed for a complete second-order wide-sense characterization (Picinbono 1996; Picinbono and Bondon 1997; Schreier and Scharf 2003a,2003b).

In this section, results analogous to those stated in Theorems 2.4.7 and 2.4.13 are presented for the conjugate covariance of the cyclic cross-correlogram.

By reasoning as for Theorem 2.4.7, we get the following result.

Theorem 3.7.1 Conjugate Covariance of the Cyclic Cross-Correlogram. Let y(t) and x(t) be zero-mean wide-sense jointly GACS stochastic processes with cross-correlation function (2.31c). Under Assumptions 2.4.2–2.4.5, the conjugate covariance of the cyclic cross-correlogram is given by

(3.132)

where

(3.13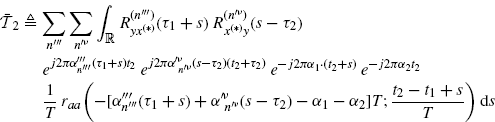3)

(3.134)

(3.135)

with

(3.136)

In (3.133)–(3.135), for notational simplicity, , , , and .

By reasoning as for Theorem 2.4.13, we get the following result.

Theorem 3.7.2 Asymptotic Conjugate Covariance of the Cyclic Cross-Correlogram. Let y(t) and x(t) be zero-mean wide-sense jointly GACS stochastic processes with cross-correlation function (2.31c). Under Assumptions 2.4.2–2.4.5, and 2.4.8, the asymptotic conjugate covariance of the cyclic cross-correlogram is given by

(3.137)

where

(3.138)

(3.139)

(3.140)

with .