2.9
Structure and Electron Transport in Irradiated Monolayer Graphene
I. Shlimak, A.V. Butenko, E. Zion, V. Richter, Yu. Kaganovskii, L. Wolfson, A. Sharoni, A. Haran, D. Naveh, E. Kogan and M. Kaveh
Department of Physics and Faculty of Engineering, Jack and Pearl Institute of Advanced Technology, Bar Ilan University, 52900 Ramat Gan, Israel
1 Introduction
Disordered graphene has attracted the attention of many researchers.1–3 Mainly, this is due to the possibility of obtaining a high-resistance state of graphene films, which is of interest for application in electronics. Experimentally, the disorder is achieved in various ways: by oxidation,4 hydrogenation,5 chemical doping,6 and irradiation by different ions with different energies.7–11 In this chapter, we discuss ion bombardment as a way of gradually inducing disorder in monolayer graphene.
2 Samples
The initial specimens were purchased from the Graphenea company, who grew monolayer graphene by chemical vapor deposition (CVD) on a copper catalyst and used a wet transfer process to move it to a 300 nm SiO2/Si substrate. The typical specimen size was 5 × 5 mm. Graphene films of such a large area are not monocrystalline but rather polycrystalline with an average microcrystal size of up to 10 µm.
On one of these specimens, gold electrical contacts were deposited directly on the graphene surface through a metallic mask (reference sample 0). On the other 5 × 5 mm specimens, many small devices of 200 × 200 µm area were prepared by e-beam lithography (EBL), with Ti/Pd 5:45 nm metal electrical contacts. All small samples on the surface of the 5 × 5 mm specimen were divided into six groups: one group was not irradiated (sample 1), whereas the other groups were irradiated with 35 keV C+ ions at five doses: 5 × 1013, 1 × 1014, 2 × 1014, 4 × 1014, and 1 × 1015 cm−2 (samples 2–6, respectively).
3 Raman scattering (RS) spectra
In the Raman spectra measurements, the samples were excited with a λ = 532 nm laser beam at low power (<2 mW) to avoid heating and film damage. Figure 1(a) compares the Raman spectra of the unirradiated reference sample 0 and sample 1, which was also not irradiated but had gone through EBL. Reference sample 0 has a typical Raman spectrum for monolayer graphene film,7 consisting of three main lines: a weak D-line at 1350 cm−1 related to the intervalley double resonant process in graphene with defects (edges, vacancies, etc.); a 2D-line at 2700 cm−1 related to an intervalley two-phonon mode, characteristic of the perfect crystalline honeycomb structure; and a graphite-like G-line at 1600 cm−1 that is common for different carbon-based films. Usually, the intensity ratio ID/IG between the D- and G-lines is used as a measure of disorder in graphene films. This ID/IG ratio was ∼0.15 in the reference sample 0, indicating that the initial large specimen was of reasonably good quality, albeit not perfect.
Analogous measurements on sample 1 showed that ID/IG increased from ∼0.15 to ∼1.8 (see Fig. 1(a)). It means that EBL introduces disorder even without ion irradiation. The damage in our case could be due to the lift-off process during EBL near the edges of the polycrystalline film.

Figure 1 Raman spectra of graphene monolayers. (a) Reference sample 0 versus sample 1 (nonirradiated, but after EBL); (b) samples 1–6 versus irradiation dose in cm−2: 0 (sample 1), 5 × 1013 (2), 1014 (3), 2 × 1014 (4), 4 × 1014 (5), and 1015 (6). The lines are shifted for clarity.
Ion bombardment leads to further increase in disorder. Figure 1(b) shows the transformation of the Raman spectra in samples 2–6 with increasing irradiation dose Φ. As the dose increases to Φ = 1 × 1014 cm−2, the amplitude of the defect-associated D-line increases, while the crystalline 2D-line quickly disappears. Furthermore, new defect lines appear: the D′ line at 1620 cm−1 and (D+G)-line at 2950 cm−1. As for the G-line, it remains approximately constant, broadening slightly because of the appearance of the nearby D′-line. At Φ = 1 × 1014 cm−2, the increasing intensity of the D-line enhances the ID/IG ratio to ∼3.2. Further increase in the dose leads to decrease and broadening of the D-line, so ID/IG decreases. At higher doses, the G-line also broadens and becomes weaker; eventually, at the maximum 1 × 1015 cm−2 dose all Raman scattering structure disappears (sample 6). We are not aware of any reports of all RS lines disappearing in disordered graphene. Usually, dependence of ID/IG on irradiation-induced disorder displays two different behaviors. In the “low defect density” regime, ID/IG increases with irradiation dose Φ, whereas in the “high defect density” regime ID/IG falls with as Φ increases because the amorphization of the graphene structure attenuates all Raman peaks. However, the complete disappearance of all RS lines cannot be explained by amorphization because G-line is observed even in amorphous carbon films.12 We assume that at the maximum level of disorder achieved in our experiments, the graphene film ceases to be continuous and splits into separate spots of small size (quantum dots). The small size of the quantum dots makes it impossible to form phonons responsible for the structural line in the RS.
The degree of disorder can be characterized by the concentration of defects ND or by the mean distance between defects LD = ND−1/2. Our irradiation conditions (35 keV C+ ions) were the same as used by Buchowicz et al.,8 chosen such that the end-of-range damage would be away from the graphene film. In this case, concentration of induced defects ND is much less than the dose Φ: ND = kΦ, where ![]() . Simulations showed that for our case,
. Simulations showed that for our case, ![]() .13
.13
We will use the empirical model that describes the dependence of ID/IG versus LD in both low and high defect density regimes developed by Lucchese et al.14 In this model, a single defect causes modification of two different length scales, rA and rS (rA > rS). In the immediate vicinity of a defect, the area ![]() is structurally disordered, but at
is structurally disordered, but at ![]() , the lattice structure is saved, though the proximity to a defect leads to breaking of selection rules and contribution to the D-line. The activated area responsible for the D-line is
, the lattice structure is saved, though the proximity to a defect leads to breaking of selection rules and contribution to the D-line. The activated area responsible for the D-line is ![]() . In the low defect density regime, the D-line intensity linearly increases with ND, which means that ID/IG ∼ LD−2. The maximum value of ID is achieved when LD falls down to rA. Further decrease of LD leads to overlap between A and S areas, at which point the ID/IG ratio begins to fall. The final equation for the dependence ID/IG on LD has the form15
. In the low defect density regime, the D-line intensity linearly increases with ND, which means that ID/IG ∼ LD−2. The maximum value of ID is achieved when LD falls down to rA. Further decrease of LD leads to overlap between A and S areas, at which point the ID/IG ratio begins to fall. The final equation for the dependence ID/IG on LD has the form15
Figure 2 shows the result of fitting the theoretical curve (1) with experimental data. First, the experimental points for irradiated samples 2–6 were plotted. We choose k = 6%; LD for these samples was defined as LD = (0.06Φ)−1/2. Then, the curve (1) was calculated to fit the experimental points. The best fit shown in Fig. 2 was obtained for CA = 5.3, CS = 0, rS = 1.8 nm, and rA = 5.5 nm. Finally, the values of ID/IG for two nonirradiated samples – the reference sample 0 and the post-EBL sample 1 – were placed on the curve for the purposes of LD (and hence ND) estimation. We obtain ND ∼ 8 × 1010 cm−2 in the reference sample 0 and ND ∼ 1012 cm−2 in sample 1.

Figure 2 Ratio ID/IG versus mean distance between defects LD. Solid line represents Eq. (1) with CA = 5.3, CS = 0, rS = 1.8 nm, and rA = 5.5 nm. Numbers near the points indicate sample number.
4 Sample resistance
Room-temperature measurements of the current–voltage (I–V) characteristics for all samples showed that for highly irradiated samples 5 and 6, the I–V is strongly nonlinear even at very small currents. For this reason, we have focused our studies of the temperature dependence of sample resistance R(T) to samples 0–4. (We note that the resistance was equal to resistivity due to the square shape of samples.) The R(T) was measured by two-probe method in a helium cryostat down to T = 1.8 K in magnetic fields B up to 4 T. Figure 3 shows R(T) curves on a log–log scale for samples 0–4 in zero B field. Sample 0 shows typical metallic behavior, when R slightly decreases with decrease of T. For sample 1, R slightly increases with decreasing T, characteristic for a “dirty” metal. For other samples, R changes with T exponentially, which is characteristic for strongly localized carriers.

Figure 3 Resistivity of disordered monolayer graphene samples versus temperature T, with sample numbers indicated. Inset shows the density of structural defects ND in samples.15
• Weak localization (WL)
Plot of the temperature dependence of conductivity on the scale σ versus ln(T) in Fig. 4 shows logarithmic behavior of σ at low T, characteristic of weak localization (WL).16 The WL regime in monolayer graphene is interesting due to the fact that charge carriers are chiral Dirac fermions that reside in two nonequivalent valleys at the K and K′ points of the Brillouin zone. Due to chirality, Dirac fermions acquire a phase of π upon intravalley scattering, which leads to destructive interference with its time-reversed counterpart and weak antilocalization (WAL). Intervalley scattering leads to restoration of WL because fermions in K and K′ valleys have opposite chiralities.

Figure 4 Conductivity of sample 1 versus ln(T). Circles and squares present experimental data, and theoretical calculation with parameters determined from fitting the magnetoconductance in Fig. 5. These parameters are shown in inset: Bφ and Bi (solid and dashed lines, left axis) and B* (right axis).
Quantum corrections to the conductivity of graphene have been studied theoretically.17 18 It was predicted that WAL corrections will dominate at relatively high T, while WL corrections will dominate at low T. For the magnetoconductance (MC) Δσ(B, T), the theory predicts19
where ![]() and
and ![]() ,where Ψ is the digamma function,
,where Ψ is the digamma function, ![]() is the coherence time,
is the coherence time, ![]() is the intervalley scattering rate, and
is the intervalley scattering rate, and ![]() is the combined scattering rate of intravalley and intervalley scattering and of trigonal warping.
is the combined scattering rate of intravalley and intervalley scattering and of trigonal warping.
Fitting Eq. (2) to experimental data for MC of sample 1 at different temperatures is illustrated in Fig. 5. In the process of fitting, we were able to extract all three parameters ![]() entering the equation. These parameters are shown in inset in Fig. 4. One can see that, in agreement with theoretical prediction,
entering the equation. These parameters are shown in inset in Fig. 4. One can see that, in agreement with theoretical prediction, ![]() . The saturation of
. The saturation of ![]() at low temperatures is well known in classical 2D systems and may be connected with existence of dephasing centers (e.g., magnetic impurities).20 21
at low temperatures is well known in classical 2D systems and may be connected with existence of dephasing centers (e.g., magnetic impurities).20 21

Figure 5 Magnetoconductance of sample 1 versus perpendicular magnetic field B at various T: solid lines – experiment, dashed lines – Eq. (2) with fitting parameters shown in the inset of Fig. 4.
• Strong localization
Resistance of samples 2–4 exhibited pronounced insulating behavior, as shown in Fig. 3. Plotting the data on the Arrhenius scale, as ln(R) versus 1/T showed that the energy of activation continuously decreases with decreasing T, which is characteristic for the variable-range-hopping (VRH) conductivity.22 There are two kinds of VRH depending on the structure of the density of states (DOS) g(E) in the vicinity of the Fermi level EF. When g(E) = g(EF) is constant, R(T) is described by the Mott Law, also known as the “T−1/3”-law in the case of 2D conductivity:
Here CM = 13.8 is the numerical coefficient22 and a is the radius of localization.
The Coulomb interaction between localized carriers leads to appearance of a soft Coulomb gap in the vicinity of EF. In the 2D case, this gap has a linear form:
where κ is the dielectric constant of the material, leading to the Efros–Shklovskii (ES) VRH or “![]() ”-law:
”-law:
where CES = 2.8.22
Coulomb interaction can alter the DOS only near EF. Far from EF, the DOS is restored to its initial value, which is approximately equal to g(EF), as illustrated in the inset in Fig. 6. Denoting the half-width of the Coulomb gap as Δ one can conclude, therefore, that the ES dependence should be observed when kT < Δ, whereas in the opposite kT > Δ regime one should observe the Mott Law.

Figure 6 Plot of log(R) versus T−1/3 for samples 2–4 (sample numbers next to the curves). Inset shows a schematic illustration of the 2D Coulomb gap in the DOS near EF. Arrows indicate the crossover temperature TC between Mott- and ES-VRH.
In Fig. 6, log(R) is plotted versus T−1/3. At high T, R(T) follows the T−1/3 dependence for all samples, but deviations to a stronger power-law dependence are observed with decreasing T for samples 3 and 4, as the samples approach the ES-VRH behavior, which should dominate at lowest temperatures. The slopes of the straight lines on T−1/3 and T−1/2 scale give the values of TM and TES. We get correspondingly 300 and 50 K for sample 3 and 6000 and 500 K for sample 4.
In VRH, only localized states within an optimal energy band ΔE(T) near the Fermi level are involved in the hopping process. This band becomes continuously narrower with decreasing T. The crossover temperature TC can be determined from the equality ΔE(TC) = Δ, which gives23
The values of TC calculated from Eq. (6) for samples 3 and 4 are shown as arrows in Fig. 6. One can see a good agreement with experiment.
5 Hopping magnetoresistance
The magnetoresistance (MR) of samples 2–4 was measured at temperatures down to 1.8 K in perpendicular ![]() and in-plane (parallel)
and in-plane (parallel) ![]() magnetic fields up to B = 8 T. It turns out that
magnetic fields up to B = 8 T. It turns out that ![]() leads to the increase of conductivity, or negative MR, while
leads to the increase of conductivity, or negative MR, while ![]() results in positive MR at low temperatures.24 This strong anisotropy indicates unambiguously different mechanisms of MR: negative MR in perpendicular fields is connected with orbital effects, while positive MR in parallel fields is determined by the spin polarization.
results in positive MR at low temperatures.24 This strong anisotropy indicates unambiguously different mechanisms of MR: negative MR in perpendicular fields is connected with orbital effects, while positive MR in parallel fields is determined by the spin polarization.
• Negative MR in perpendicular fields
Figure 7 shows the MR curves ΔR(B)/R(0) ≡ [R(B) − R(0)]/R(0) at different T for all three samples on a log–log scale. On this scale, the slope of the curve is equal to the power α in ΔR/R ∼ Bα. Quadratic dependence (α = 2) is observed at low fields up to some value B*.

Figure 7 Negative MR of samples 2 (a), 3 (b), and 4 (c) at different T plotted on a log–log scale. Long-dashed lines correspond to the quadratic dependence ΔR/R ∼ B2, whereas short-dashed lines correspond to linear dependence.
Theoretically, the effect of orbital negative MR in the VRH regime has been discussed earlier.25–27 The idea suggested in Ref. 25 is based on the following considerations. In VRH, the hopping distance rh increases with decreasing T and becomes much larger than the mean distance between localized centers. As a result, the probability of a long-distance hop is determined by the interference of many tunneling paths via intermediate sites that may include scattering processes – see Fig. 8 for a schematic illustration. All these scattered waves together with the nonscattered direct wave contribute additively to the amplitude of the wave function ψ12 that reflects the probability for a charge carrier localized on site 1 to appear on site 2.

Figure 8 Schematics of the cigar-shaped region with localized states contributing to the probability of an electron tunneling from center 1 to center 2.
An important feature is that there is no backscattering, and scattered waves decay rapidly with increasing distance as ![]() , where ξ is the localization radius. Therefore, only the shortest paths contribute to ψ12. All these paths are concentrated in a cigar-shaped domain of the length rh, width D ≈ (rhξ)1/2, and area A ≈ rh3/2ξ1/2.
, where ξ is the localization radius. Therefore, only the shortest paths contribute to ψ12. All these paths are concentrated in a cigar-shaped domain of the length rh, width D ≈ (rhξ)1/2, and area A ≈ rh3/2ξ1/2.
As a result of averaging over different configurations, the contribution of the scattering sites to the total hopping probability vanishes due to destructive interference. The perpendicular magnetic field suppresses the interference, which leads to an increase of the hopping probability and, therefore, to the negative MR. In accordance with theoretical considerations, negative MR as a function B is linear at moderate fields and quadratic at very low fields. We assume that quadratic dependence ends at a magnetic field B* when the magnetic flux through the average cigar-shaped area ΦB = B*A will be equal to the magnetic flux quantum Φ0 = h/2e ≈ 2.07 × 10−15 Wb. This gives ![]() . The square-root dependence B* ∼ T1/2 has been indeed observed in experiment – see Fig. 9.24
. The square-root dependence B* ∼ T1/2 has been indeed observed in experiment – see Fig. 9.24

Figure 9 The values of B* as a function of T1/2. The sample numbers are indicated near the straight lines.
We also use the values of B* in an attempt to normalize the negative MR data for all samples and temperatures below 25 K. In Fig. 10, MR curves on a linear scale are plotted as a function of dimensionless parameter B/B*. One can see that all curves are fully described by a single common magnetic field dependence.

Figure 10 Negative MR curves for different samples and temperatures plotted versus  . The arrows and numbers show the end of each curve and indicate samples (2, 3, 4) and T. The inset shows negative MR data for small values
. The arrows and numbers show the end of each curve and indicate samples (2, 3, 4) and T. The inset shows negative MR data for small values  .
.
• Positive MR in parallel fields
In our samples, positive MR in parallel fields was observed at low temperatures (see Fig. 11). Earlier, positive MR in VRH regime had been observed in different 2D systems, particularly in a 2D electron gas formed in a GaAs/AlxGa1−x heterostructure.28 The parallel magnetic field couples only to the electron spin, meaning that the spin state of localized electrons influences the hopping conductivity despite the fact that it is not included explicitly in Eqs (3) and (5).

Figure 11 Positive MR of sample 3 plotted as a function of 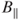 . Inset shows the MR data for low fields on a quadratic scale.
. Inset shows the MR data for low fields on a quadratic scale.
A possible mechanism of positive MR was suggested by Kurobe and Kamimura29 and studied in more detail in Ref. 30. In this model, it is recognized that a certain fraction of the states can accommodate two electrons. Double occupancy is possible if the on-site Coulomb repulsion U between the electrons is smaller than the energy distribution occupied by localized states. It was already mentioned that in VRH, only localized states with energy level within the narrow optimal band of width ΔE(T) around EF are involved in the hopping process. However, for some states, which cannot participate in VRH at a given temperature because the energy of the first electron E(1) is well below EF, the energy of the second electron E(2) = E(1) + U may be located just within the optimal band. This allows those states to participate in the VRH at zero magnetic field. In the strong field limit, all spins are polarized and, therefore, transitions through the double occupied states are suppressed, resulting in positive MR. In this mechanism, contribution of the doubly occupied states in zero-field VRH is significant only when the width of the optimal band ΔE(T), which decreases with T, falls below U. In the opposite limit, ![]() , the localized states will either participate or not participate in VRH independently of the existence of doubly occupied states. This explains why positive MR is observable only at low T. At moderate fields, theory predicts the linear dependence ΔR/R ∼ B, while at weak fields one expects30 a quadratic dependence, ΔR/R ∼ B2. This prediction agrees with experiment, as shown in Fig. 11. Theory also predicts that positive MR should saturate at strong fields when all electron spins are polarized. In our samples, no saturation was observed in magnetic fields up to 8 T.
, the localized states will either participate or not participate in VRH independently of the existence of doubly occupied states. This explains why positive MR is observable only at low T. At moderate fields, theory predicts the linear dependence ΔR/R ∼ B, while at weak fields one expects30 a quadratic dependence, ΔR/R ∼ B2. This prediction agrees with experiment, as shown in Fig. 11. Theory also predicts that positive MR should saturate at strong fields when all electron spins are polarized. In our samples, no saturation was observed in magnetic fields up to 8 T.
References
- 1. M. I. Katsnelson, Graphene: Carbon in Two Dimensions, Cambridge, UK: Cambridge University Press, 2012.
- 2. L. E. F. Foa Torres, S. Roche, and J.-C. Charlier, Introduction to Graphene-Based Nanomaterials: From Electronic Structure to Quantum Transport, Cambridge, UK: Cambridge University Press, 2014.
- 3. J. H. Warner, F. Schaffel, M. Rummeli, and A. Bachmatiuk, Graphene: Fundamentals and Emergent Applications, Amsterdam: Elsevier, 2012.
- 4. L. Liu, S. Ryu, M. R. Tomasik, et al., “Graphene oxidation: Thickness-dependent etching and strong chemical doping,” Nano Lett. 8, 1965–1970 (2008).
- 5. D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, et al., “Control of graphene's properties by reversible hydrogenation: Evidence for graphane,” Science 323, 610–613 (2009).
- 6. H. Liu, Y. Liu, and D. Zhu, “Chemical doping of graphene,” J. Mater. Chem. 21, 3335–3345 (2011).
- 7. R. Saito, M. Hofmann, G. Dresselhaus, A. Jorio, M. S. Dresselhaus, “Raman spectroscopy of graphene and carbon nanotubes,” Adv. Phys. 30, 413–550 (2011).
- 8. G. Buchowicz, P. R. Stone, J. T. Robinson, C. D. Cress, J. W. Beeman, and O. D. Dubon, “Correlation between structure and electrical transport in ion-irradiated graphene grown on Cu foils,” Appl. Phys. Lett. 98, 032102 (2011).
- 9. B. Guo, Q. Liu, E. Chen, H. Zhu, L. Fang, and J. R. Gong, “Controllable N-doping of graphene,” Nano Lett. 10, 4975–4980 (2010).
- 10. Q. Wang, W. Mao, D. Ge, Y. Zhang, Y. Shao, and N. Ren, “Effects of Ga ion-beam irradiation on monolayer graphene,” Appl. Phys. Lett. 103, 073501 (2013).
- 11. A. C. Ferrari, J. C. Meyer, V. Scardaci, et al., “Raman spectrum of graphene and graphene layers,” Phys. Rev. Lett. 97, 187401 (2006).
- 12. A. C. Ferrari and J. Robertson, “Interpretation of Raman spectra of disordered and amorphous carbon,” Phys. Rev. B 61, 14095–14107 (2000).
- 13. O. Lehtinen, J. Kotakoski, A. V. Krasheninnikov, A. Tolvanen, K. Nordlund, and J. Keinonen, “Effects of ion bombardment on a two-dimensional target: Atomistic simulations of graphene irradiation,” Phys. Rev. B 81, 153401 (2010).
- 14. M. M. Lucchese, F. Stavale, E. H. Ferreira, et al., “Quantifying ion-induced defects and Raman relaxation length in graphene,” Carbon 48, 1592–1597 (2010).
- 15. I. Shlimak, A. Haran, E. Zion, et al., “Raman scattering and electrical resistance of highly disordered graphene,” Phys. Rev. B 91, 045414 (2015).
- 16. B. L. Altshuler, A. G. Aronov, and D. E. Khmelnitsky, “Effects of electron–electron collisions with small energy transfers on quantum localization,” J. Phys. C: Solid State Phys. 15, 7367–7386 (1982).
- 17. I. L. Aleiner and K. B. Efetov, “Effect of disorder on transport in graphene,” Phys. Rev. Lett. 97, 236801 (2006).
- 18. P. M. Ostrovsky, I. V. Gornyi, and A. D. Mirlin, “Electron transport in disordered graphene,” Phys. Rev. B 74, 235443 (2006).
- 19. E. McCann, K. Kechedzhi, V. I. Fal'ko, H. Suzuura, T. Ando, and B. L. Altshuler, “Weak-localization magnetoresistance and valley symmetry in graphene,” Phys. Rev. Lett. 97, 146805 (2006).
- 20. D. J. Bishop, D. C. Tsui, and R. C. Dines, “Non-metallic conduction in electron-inversion layers at low temperatures,” Phys. Rev. Lett. 44, 1153–1156 (1980).
- 21. V. F. Gantmakher, Electrons and Disorder in Solids, New York: Oxford University Press, 2005.
- 22. B. I. Shklovskii and A. L. Efros, Electronic Properties of Doped Semiconductors, Berlin: Springer-Verlag, 1984.
- 23. E. Zion, A. Haran, A. V. Butenko, et al., “Localization of charge carriers in monolayer graphene gradually disordered by ion irradiation,” Graphene 4, 45–53 (2015).
- 24. I. Shlimak, E. Zion, A. V. Butenko, et al., “Hopping magnetoresistance in ion irradiated monolayer graphene,” Physica E 76, 158–163 (2016).
- 25. V. L. Nguen, B. Z. Spivak and B. I. Shklovskii, “Tunnel hopping in disordered systems,” Sov. Phys. JETP 62, 1021–1029 (1985).
- 26. B. I. Shklovskii and B. Z. Spivak, “Scattering and interference effects in variable range hopping conduction,” chapter in: M. Pollak and B. Shklovskii, eds. Hopping Transport in Solids, Amsterdam: Elsevier, 1991, p. 217.
- 27. W. Schirmacher, “Quantum-interference magnetoconductivity in the variable-range hopping-regime,” Phys. Rev. B 41, 2461–2468 (1990).
- 28. I. Shlimak, S. I. Khondaker, M. Pepper, and D. A. Ritchie, “Influence of parallel magnetic fields on a single-layer two-dimensional electron system with a hopping mechanism of conductivity,” Phys. Rev. B 61, 7253–7256 (2000).
- 29. A. Kurobe and H. Kamimura, “Correlation-effects on variable-range-hopping conduction and the magnetoresistance,” J. Phys. Soc. Japan 51, 1904–1913 (1982).
- 30. K. A. Matveev, L. I. Glazman, P. Clark, D. Ephron, and M. R. Beasley, “Theory of hopping magnetoresistance induced by Zeeman splitting,” Phys. Rev. B 52, 5289–5297 (1995).

