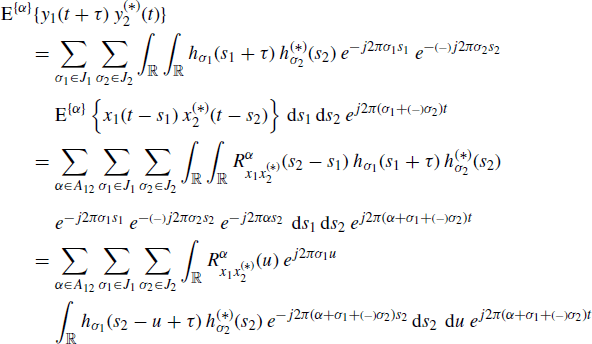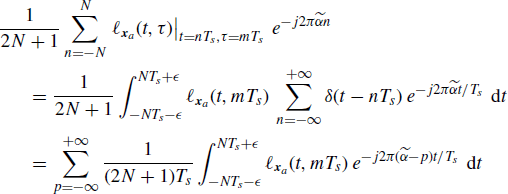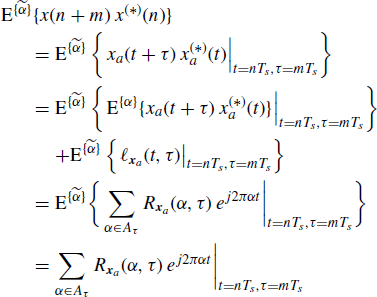6.5 Proofs of FOT Counterparts of Some Results on ACS and GACS Signals

In this section, proofs of some results presented in Section 1.3 in the stochastic approach are carried out in the functional approach. Moreover, when possible, results are derived in the more general case of GACS signals.

6.5.1 Proof of FOT Counterpart of (1.114)

By substituting (1.112) into (1.113) we have

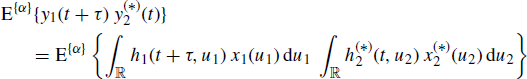
(6.79)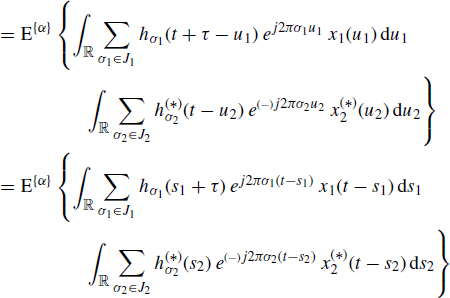

where, in the last equality, the variable changes s₁ = t − u₁ and s₂ = t − u₂ are made. Thus by assuming that the order of sum, integral, and almost-periodic component extraction operations can be interchanged, and observing that almost-periodic functions can be led outside the almost-periodic component extraction operator, we get

(6.80)

where, in the last equality, the variable change s₂ − s₁ = u is made and, according to (1.95) (with the replacements and ), we put

(6.81)

By substituting (1.115) into (6.80), we get the FOT counterpart of (1.114) which is formally the same as (1.114).

6.5.2 Proof of FOT Counterpart of (1.116)

By taking the Fourier coefficient at frequency β of the almost periodic-function in the FOT counterpart of (1.114), we have

(6.82)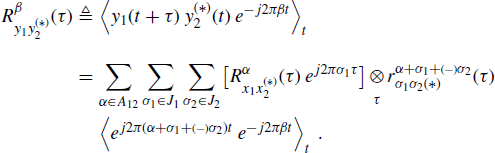

Since

(6.83)

the FOT counterpart of (1.116), which is formally identical to (1.116), easily follows.

6.5.3 Proof of FOT Counterparts of (1.135) and (1.136)

By using the FOT counterparts of (1.131) and (1.132), which are formally identical to (1.131) and (1.132), we get

(6.84)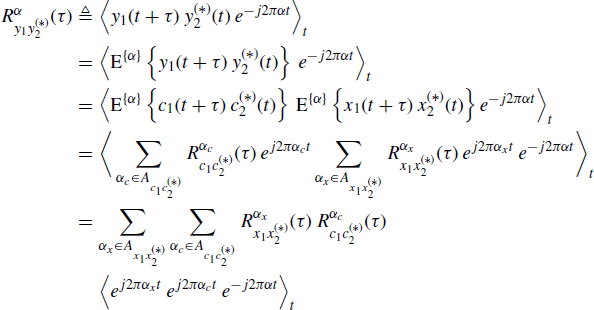

from which the FOT counterpart of (1.135), formally identical to (1.135), follows observing that

(6.85)

The FOT counterpart of (1.136) easily follows by Fourier transforming both sides of the FOT counterpart of (1.135).

6.5.4 Proof of the FOT Counterpart of (1.173) for GACS Signals

Let , , be the discrete-time signal obtained by uniformly sampling the complex-valued continuous-time signal x_a(t) with sampling period T_s = 1/f_s. The FOT counterpart of (1.173) is

(6.86)

where E^{α}{ · } is the continuous-time almost-periodic component extraction operator (see (6.22)) and is the discrete-time almost-periodic component extraction operator which is defined similarly to its continuous-time counterpart.

Proof: The second-order lag product can be decomposed into the sum of its almost-periodic component and a residual term not containing any finite-strength additive sinewave component (Section 6.3.3). For a GACS signal, the result is that

(6.87)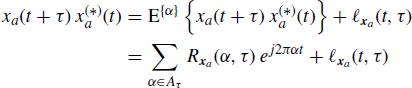

where , , and

(6.88)

For any 0 < < T_s we formally have

(6.89)

where, in the second equality, the Poisson sum formula

(6.90)

is accounted for. Taking the limit for N→ ∞ in (6.89) and accounting for (6.88) one has

(6.91)

That is, if the continuous-time residual term does not contain any (continuous-time) finite-strength additive sinewave component (see (6.88)), then also the sampled residual term does not contain any discrete-time finite-strength additive sinewave component.

Thus,

(6.92)

where in the third equality (6.91) is accounted for and in the last equality the fact that the right-hand side of (6.92) is a discrete-time almost periodic function is exploited.

Equation (6.86) is then proved observing that the right-hand side of (6.92) is coincident with the right-hand side of (6.86).

Note that, as in the stochastic approach, uniformly sampling a continuous-time GACS signal leads to a discrete-time ACS signal (Theorem 2.5.2).