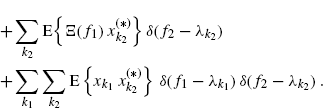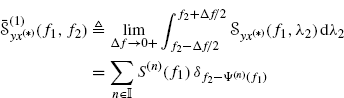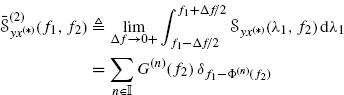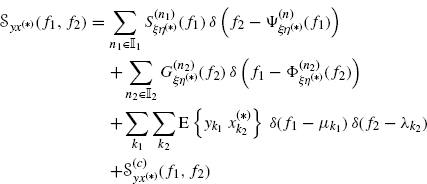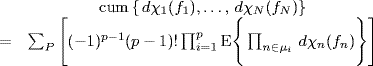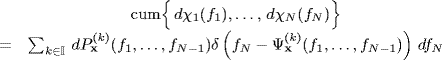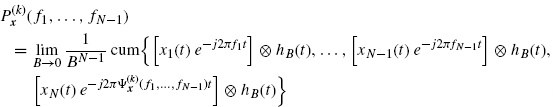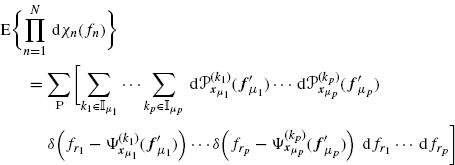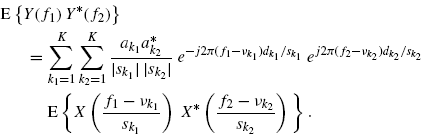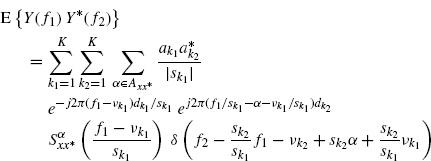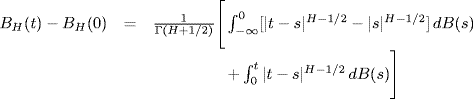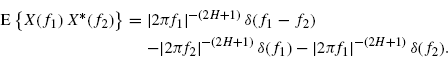4.2 Characterization of SC Stochastic Processes

In this section, spectrally correlated stochastic processes are introduced (Definitions 4.2.4–4.2.8) and characterized (Theorems 4.2.7 and 4.2.9). Moreover, examples of applications where such processes occur are presented.

4.2.1 Second-Order Characterization

Definition 4.2.1 A covariance function is said to be harmonizable if there exists a spectral covariance function of bounded variation on

(4.1)

such that

(4.2)

where the integral is a Fourier-Stieltjes transform (Loève 1963).

Definition 4.2.2 A second-order stochastic process is said to be (strongly) harmonizable if there exists a second-order stochastic process χ(f) with increments dχ(f) having covariance function with of bounded variation on such that

(4.3)

with probability one (Loève 1963).

The function χ(f) is named integrated spectrum (Gardner 1985, Section 10.1.2).

In (Loève 1963), it is shown that a necessary condition for a stochastic process to be harmonizable is that it is second-order continuous (or mean-square continuous) (Definition 2.2.11, Theorem 2.2.12). Moreover, it is shown that a stochastic process is harmonizable if and only if its covariance function is harmonizable. In fact, convergence of integrals in (4.2) and (4.3) is in the mean-square sense. In (Hurd 1973), the harmonizability of processes obtained by some processing of other harmonizable processes is studied.

In the following, the spectral characterization of stochastic processes will be provided in the sense of distributions (generalized functions) (Gelfand and Vilenkin 1964, Chapter 3), (Henniger 1970). Instead of considering Fourier-Stieltjes transforms as in (4.2) and (4.3), integrals have to be intended as Lebesgue integrals if the argument is a summable function and as formal representations for functional operators if the argument is a distribution (e.g., a Dirac delta) (Gardner 1985, Section 10.1.2), (Papoulis 1991, Section 12-4). Therefore, χ(f) and are assumed to have zero singular component (Cramér 1940).

Furthermore, all the ordinary functions are assumed to be Lebesgue measurable and considerations made at the beginning of Section 3.4 hold.

Definition 4.2.3 Let be a second-order complex-valued harmonizable stochastic process. Its bifrequency spectral correlation function or Loève bifrequency spectrum (Loève 1963), (Thomson 1982), also called generalized spectrum in (Gerr and Allen 1994), cointensity spectrum in (Middleton 1967), or dual frequency spectral correlation in (Hanssen and Scharf 2003), is defined as

(4.4)

In (4.4),

(4.5)

is the Fourier transform of x(t) and is assumed to exist (at least) in the sense of distributions (Gelfand and Vilenkin 1964, Chapter 3), (Henniger 1970) w.p.1.. Superscript (*) denotes an optional complex conjugation.

The functions defined in (4.4) and (4.5) can be linked to those in (4.2) and (4.3). In fact, even if γ(f₁, f₂) and χ(f) contain first kind discontinuities (jumps), in the sense of distributions we can formally write (Gardner 1985, Section 10.1.2), (Papoulis 1991, Section 12-4)

(4.6)

(4.7)

Such representation does not hold in the presence of singular components (Hurd and Miamee 2007, p. 197).

Note that, two functions are defined in (4.4) depending on the choice of conjugating or not the second term even if, in general, only the function with the conjugation is named bifrequency spectrum and is considered in the literature. Both possibilities on (*) need to be considered, however, in dealing with nonstationary complex signals (Thomson 1982), (Picinbono and Bondon 1997), (Schreier and Scharf 2003a), (Schreier and Scharf 2003b).

The Loève bifrequency spectrum (4.4) is the statistical correlation between the spectral components of x(t) at frequencies f₁ and f₂. It is well known that for second-order WSS stochastic processes the bifrequency spectrum (with (*) present) is zero unless f₁ = f₂. Then, the presence of spectral correlation for f₁ ≠ f₂ can be adopted to detect the presence of nonstationarity in the data (Thomson 1982), (Hurd 1988, 1991), (Hurd and Gerr 1991), (Allen and Hobbs 1992), (Genossar 1992), (Dehay and Hurd 1994), (Gerr and Allen 1994), (Varghese and Donohue 1994).

Definition 4.2.4 A complex-valued second-order harmonizable stochastic process , is said to be spectrally correlated if its Loève bifrequency spectrum can be expressed as

(4.8)

where denotes Dirac delta, is a countable set, the curves , describe the support of , and the functions , referred to as spectral correlation density functions, describe the density of the Loève spectrum on its support curves.

According to (Lii and Rosenblatt 2002) where the special case of support lines is considered, the curve is said a support curve if in a set of positive one-dimensional Lebesgue measure.

Note that the functions depend on the choice made for (*), can always be chosen invertible if no correlation exists along lines with f₁ = constant, but cannot be arbitrary since the symmetry condition needs to be satisfied (Picinbono and Bondon 1997). Furthermore, the functions and can always be chosen such that the set

(4.9)

is at most countable . In such a case, the condition of bounded variation of the covariance can be written as

(4.10)

which is the generalization to SC processes of eq. (4.4) in (Hurd 1991) derived for ACS processes (see also (10) in (Hurd 1989a) and (13) in (Ogura 1971) for the case of cyclostationary processes).

From Definition 4.2.4, it follows that the process x(t) does not contain a deterministic or random almost-periodic component (Section 1.2.7). In fact, if

(4.11)

with ξ(t) zero-mean and SC according to Definition 4.2.4 and x_k deterministic coefficients or random variables, then, denoting by Ξ(f) the Fourier transform in the sense of distributions of ξ(t), we have the following expression for the Loève bifrequency spectrum of x(t):

(4.12)

where

(4.13)

is the Loève bifrequency spectrum of the SC process ξ(t).

From Definition 4.2.4, it follows that SC processes are those nonstationary processes for which the Loève bifrequency spectrum is constituted by spectral masses located on a countable set of support curves in the bifrequency plane (f₁, f₂). If the process x(t) contains a deterministic or random almost-periodic component, then also isolated points and lines parallel to the frequency axis are present in the support of the Loève bifrequency spectrum. Strictly speaking, terms with can be accommodated by (4.8). This case, however, will be excluded in the following by assuming the functions invertible.

More generally, the Loève bifrequency spectrum can be constituted by both an impulsive and a continuous part.

Definition 4.2.5 A complex-valued second-order harmonizable stochastic process with no finite-strength additive sinewave components, is said to exhibit spectral correlation if its Loève bifrequency spectrum can be expressed as

(4.14)

where is a continuous function.

Nonstationary processes with are treated in (Soedjack 2002), where a consistent estimator of is obtained by using several realizations of the stochastic process. In (Allen and Hobbs 1997) a consistent estimator based on a single realization is proposed for the case of nonstationary white noise.

A single SC stochastic process is also said singularly SC if a distinction is necessary with the joint spectral correlation property of two different processes.

Definition 4.2.6 Two complex-valued second-order harmonizable stochastic processes and are said jointly SC if their bifrequency cross-spectrum is constituted by spectral masses located on a countable set of support curves in the bifrequency plane (f₁, f₂), that is,

(4.15)

where is a countable set, the functions can always be chosen invertible, and the functions are referred to as the spectral cross-correlation density functions.

In the following, for notation simplicity, when this does not generate ambiguity, we will put

Moreover, with reference to definitions given in the following Theorem 4.2.7, we will put

Accounting for the fact that and (Zemanian 1987, Section 1.7), with Φ⁽ⁿ⁾(·) denoting the inverse function of Ψ⁽ⁿ⁾(·), and and the derivatives of Φ⁽ⁿ⁾(·) and Ψ⁽ⁿ⁾(·), respectively, and by using the sampling property of the Dirac delta, the following result can be proved.

Theorem 4.2.7 Let and be continuous-time complex-valued second-order jointly harmonizable stochastic processes not containing any additive finite-strength sinewave component. If the processes are jointly spectrally correlated, then their Loève bifrequency cross-spectrum can be expressed in one of the two equivalent forms

(4.16a)

(4.16b)

In (4.16a) and (4.16b), δ(·) is Dirac delta, is a countable set, the curves f₂ = Ψ⁽ⁿ⁾(f₁) or, equivalently, f₁ = Φ⁽ⁿ⁾(f₂), describe the support of , and the complex-valued functions S⁽ⁿ⁾(f₁) and G⁽ⁿ⁾(f₂), called spectral correlation density functions, represent the density of the Loève bifrequency spectrum on its support curves. The functions S⁽ⁿ⁾(f₁) and G⁽ⁿ⁾(f₂) are not unambiguously determined since each of them can be expressed as sum of more functions with non overlapping supports. Assuming that the functions Ψ⁽ⁿ⁾(f₁) and Φ⁽ⁿ⁾(f₂) are not constant within intervals of positive Lebesgue measure, the functions S⁽ⁿ⁾(f₁) and G⁽ⁿ⁾(f₂) can be chosen with supports such that Ψ⁽ⁿ⁾(·) and Φ⁽ⁿ⁾(·) are invertible functions and the curves f₂ = Ψ⁽ⁿ⁾(f₁) and for n ≠ n′ intersect at most in a countable set of points. If the real-valued functions Ψ⁽ⁿ⁾(·) are assumed to be differentiable, Φ⁽ⁿ⁾(·) are their inverse and are also differentiable, then

(4.17a)

(4.17b)

where superscript ′ denotes derivative.

The differentiability assumption for both Ψ⁽ⁿ⁾(·) and Φ⁽ⁿ⁾(·) prevents that their derivatives are zero or infinity. This assumption is fulfilled in all practical cases considered in Section 4.2.4 except the fBm. Such an assumption can be relaxed by considering differentiability almost everywhere and the possibility of derivatives equal to zero or infinity, even in frequency intervals with nonzero Lebesgue measure, as it happens in (4.12) or for the fBm discussed in Section 4.2.4. In such a case, results similar to those subsequently derived hold, but proofs are more cumbersome.

The assumption that y(t) and x(t) do not contain additive finite-strength sinewave components, say and prevents that the Loève bifrequency cross-spectrum (4.15) contains spectral masses concentrated in isolated points of the bifrequency plane or on lines parallel to the frequency axes. That is, the Loève bifrequency cross-spectrum does not contain additive terms as , , and , with g₁(f₁) and g₂(f₂) functions depending on x(t) and y(t) (see (4.12) for the case y ≡ x).

The bounded variation condition (4.1), which is consequence of the harmonizability assumption, in the case of jointly SC processes can be written as

(4.18)

Definition 4.2.8 Given two complex-valued second-order harmonizable jointly SC stochastic processes and , their bifrequency spectral cross-correlation density function is defined as

(4.19)

where δ_f denotes Kronecker delta (i.e., δ_f = 1 for f = 0 and δ_f = 0 otherwise).

The function is named bifrequency spectral cross-correlation density function since it is the generalization to SC processes (and two frequency arguments) of the spectral cross-correlation density function defined for ACS processes in (Gardner 1986a), (Gardner 1987d), and (Gardner 1991b). For any pair (f₁, f₂), is given by the sum of all S⁽ⁿ⁾(f₁) such that f₂ = Ψ⁽ⁿ⁾(f₁). Thus, it represents the density of the spectral cross-correlation E{Y(f₁)X^(*)(f₂)} between the spectral components at frequencies f₁ and f₂ of y(t) and x(t), respectively.

The arguments of the Dirac deltas in (4.16a) and (4.16b) contain (possibly nonlinear) functions Ψ⁽ⁿ⁾(f₁) and Φ⁽ⁿ⁾(f₂), respectively. Thus, two kinds of bifrequency spectral-correlation densities should be considered, depending on which one of the two frequency variables, f₁ or f₂, is considered as independent in the argument of δ(·). Specifically, under the assumption that there is no cluster of support curves, by integrating both sides of (4.16a) w.r.t. f₂ and both sides of (4.16b) w.r.t. f₁, the following two bifrequency spectral cross-correlation density (SCD) functions can be defined:

(4.20a)

(4.20b)

In the sequel, unlike otherwise specified, the term bifrequency spectral correlation density will be used for the function that will be denoted by if it does not create ambiguity.

Representation (4.16a) for the bifrequency cross-spectrum must be used if spectral correlation exists along lines with f₂ = constant, whereas representation (4.16b) must be used if spectral correlation exists along lines with f₁ = constant. Let be

(4.21)

(4.22)

with ξ(t) and η(t) zero-mean and SC according to Definition 4.2.4 and x_k and y_k deterministic coefficients or random variables statistically independent of ξ(t) and η(t) ∀t. The most general expression for the bifrequency cross-spectrum of x(t) and y(t) which accommodates also possible spectral correlation along lines parallel to the f₁ and f₂ axes (when some of the and/or functions are constant) and a continuous term, can be obtained by splitting the support curves into two disjoint sets:

(4.23)

where the decomposition is not unique and is a continuous function.

Accounting for (4.15) and the sampling property of the Dirac delta, the following result can be proved.

Theorem 4.2.9 Second-Order Temporal Cross-Moment of Jointly SC Processes. Let and be complex-valued second-order harmonizable jointly SC stochastic processes with Loève bifrequency cross-spectrum (4.16a). The second-order temporal cross-moment of y(t) and x(t) is given by

(4.24a)

(4.24b)

(4.24c)

(4.24d)

where (−) is an optional minus sign to be considered only if (*) is present, denotes convolution with respect to t₁,

(4.25)

(4.26)

and the Fourier transforms are in the sense of distributions (Gelfand and Vilenkin 1964), (Henniger 1970), (Zemanian 1987).

Proof: See Section 5.1.

Theorem 4.2.10 Time-Variant Cross-Spectrum of Jointly SC Processes. Let and be complex-valued second-order harmonizable jointly SC stochastic processes with Loève bifrequency cross-spectrum (4.16a). The time-variant cross-spectrum of y(t) and x(t) is given by

(4.27a)

(4.27b)

Proof: See Section 5.1.

From (4.27b) it follows that the time-variant cross-spectrum of jointly SC processes is an almost periodic function of t with both coefficient and frequencies depending on f.

The class of the SC stochastic processes includes, as a special case, the class of the second-order wide-sense ACS processes which, in turn, includes the class of the second-order WSS processes. For ACS processes, the support of the bifrequency spectrum in the bifrequency plane is constituted by lines with unit slope (Hurd 1989a), (Dehay and Hurd 1994). Consequently, the separation between correlated spectral components assumes values belonging to a countable set. Such values, called cycle frequencies, are the frequencies of the Fourier series expansion of the almost-periodically time-variant statistical autocorrelation function (Gardner 1987d), (Dehay and Hurd 1994). Thus, for ACS processes, a one-to-one correspondence exists between elements and cycle frequencies α, and

(4.38)

Furthermore, the spectral correlation density functions are coincident with the (conjugate if (*) is absent) cyclic spectra . Therefore,

(4.29)

(4.30)

where denotes the countable set of the (conjugate) cycle frequencies and are the (conjugate) cyclic autocorrelation functions, that is, the inverse Fourier transforms of the (conjugate) cyclic spectra . Moreover, for ACS processes the time-variant spectrum (4.27a) is an almost-periodic function of t with coefficients depending on f and equal to the cyclic spectra and frequencies not depending on f and coincident with the cycle frequencies (see (1.90)). Note that the terms SC and ACS are used as synonyms in (Gardner 1987d), (Gardner 1991b), where it is considered only the case in which the separation between correlated spectral components can assume values in a countable set. WSS processes can be obtained as a special case of ACS processes when the set contains the only element α = 0. In such a case, by specializing (4.29) and (4.30), one has

(4.31)

(4.32)

where is the power spectral density function of x(t). From (4.31) and (4.32) it is evident that a zero-mean stochastic process x(t) is WSS (i.e., is a function of t₁ − t₂) if and only if no correlation exists between spectral components that are separated (i.e., is concentrated on the diagonal f₂ = f₁ of the bifrequency plane). If the process is also circular (i.e., R_xx(t₁, t₂) ≡ 0 (Picinbono and Bondon 1997)), then it also results S_xx(f₁, f₂) ≡ 0.

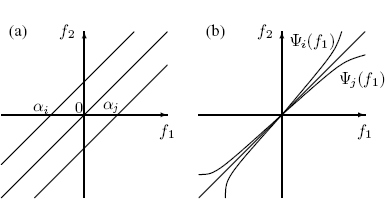
In Figures 4.1(a) and 4.1 (b), two examples of supports of Loève bifrequency spectra in the bifrequency plane are represented. The case of an ACS process is considered in Figure 4.1(a) and that of an SC not ACS process in Figure 4.1(b).

4.2.2 Relationship among ACS, GACS, and SC Processes

In Chapter 2, the class of the generalized almost-cyclostationary (GACS) processes (Izzo and Napolitano 1998b) is characterized. GACS processes exhibit an almost-periodically time-variant statistical autocorrelation function whose (generalized) Fourier series expansion has coefficients and frequencies (cycle frequencies) depending on the lag parameter. ACS processes are obtained as special case when the frequencies are constant with respect to the lag parameter.

SC processes have a Loève bifrequency spectrum with spectral masses concentrated on a countable set of curves in the bifrequency plane. ACS processes are obtained as special case of SC processes when the support curves are lines with unit slope (Hurd 1989a), (Hurd and Gerr 1991), (Dehay and Hurd 1994), (see 4.29). For ACS processes, correlation exists only between spectral components that are separated by quantities belonging to a countable set of values, the cycle frequencies. In such a case, the (conjugate) autocorrelation function E{x(t₁)x^(*)(t₂)} obtained as double inverse Fourier transform of the Loève bifrequency spectrum (4.4), as a function of t = t₂ and τ = t₁ − t₂, is almost periodic in t with frequencies equal to the cycle frequencies and independent of τ (see (4.30)).

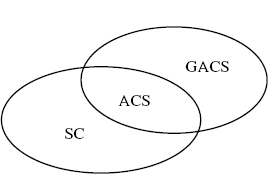
Therefore, ACS processes are obtained by the intersection of the class of the GACS processes and the class of the SC processes (Figure 4.2). In particular, ACS processes are the subclass of the GACS processes that exhibit the spectral correlation property.

4.2.3 Higher-Order Statistics

In this section, the higher-order characterization of SC processes is carried out in the frequency domain. Specifically, higher-order spectral moments and cumulants are defined and their relationships established.

Let x_i(t), (i = 1, …, N), be (possibly distinct) complex-valued harmonizable processes with Cramèr representation

(4.33)

Since the processes are denoted as distinct, without lack of generality no optional complex conjugation is necessary in the notation of the following definitions. In fact, if , then .

Accordingly with the (second-order) harmonizability definition (Definition 4.2.1) and the definitions in (Brillinger and Rosenblatt 1967), (Brillinger 1974), (Hanssen and Scharf 2003), for higher-order moment and cumulants, we have the following, where cumulants of complex variables and processes are defined according to (Spooner and Gardner 1994, App. A), (Napolitano 2007a), and Section 1.4.2.

Definition 4.2.11 The processes x_i(t), (i = 1, …, N) are said to be jointly harmonizable for the moment if there exists a spectral moment function such that

(4.34)

with

(4.35)

Definition 4.2.12 The processes x_i(t), (i = 1, …, N) are said to be jointly harmonizable for the cumulant if there exists a spectral cumulant function such that

(4.36)

with

(4.37)

Accounting for the relationships existing between moments and cumulants of real-valued random variables and processes (Leonov and Shiryaev 1959), (Brillinger 1965), (Brillinger and Rosenblatt 1967), and their extension to the complex case (Spooner and Gardner 1994, App. A), (Napolitano 2007a), (Section 1.4.2), one obtains

(4.38)

where P is the set of distinct partitions of {1, . . . , N}, each constituted by the subsets {μ_i, i = 1, . . . , p}. Moreover, it results that

(4.39)

Definition 4.2.13 Let x_i(t), (i = 1, …, N) be processes jointly harmonizable for the cumulant. The processes are said to be (Nth-order) jointly SC if

(4.40)

where x [x₁, …, x_N] and does not contain jumps. If, in addition, does not have singular component, is absolutely continuous and

(4.41)

It results that

(4.42)

where

(4.53)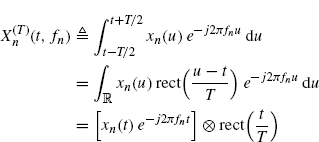

By letting h_B(t) Brect(Bt) with B = 1/T, (4.42) becomes

(4.44)

which is the Nth-order cross-cumulant of low-pass filtered versions of the frequency-shifted signals , when the frequency shifts are such that

(4.55)

and the bandwidth B of the low-pass filters h_B(t) approaches zero.

In the special case of jointly ACS processes, (4.42) and (4.44) reduce to (13.19) and (13.20) of (Gardner et al. 2006), respectively.

Cumulants are invariant with respect to permutation of the random variables. Consequently, let {i₁, …, i_N} be any permutation of {1, …, N}, one has

(4.46)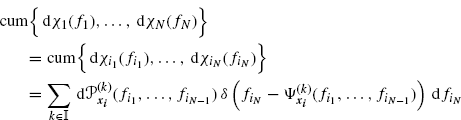

where .

Theorem 4.2.14 For every partition {μ₁, …, μ_p} of {1, …, N}, let x_n(t), n μ_i, be jointly SC. That is,

(4.47)

where the functions do not contain jumps. In (4.47), is the |μ_i|-dimensional vector whose components are those of x having indices in μ_i, with |μ_i| the number of elements in μ_i, r_i represents the last element in μ_i, and each partition is ordered so that μ_p always contains N as last element (i.e., r_p = N). Moreover, and is a countable set. If, in addition, the functions do not have singular components, they are are absolutely continuous and

(4.48)

where , with .

By substituting (4.47) into (4.39) the result is that

(4.49a)

(4.49b)

where the second equality holds if all are absolutely continuous.

In the absence of singular components, the following notation can be used (Section 1.1.2 and Definition 4.2.3)

(4.50)

(4.51)

The above definitions and results specialize to first-and second-order as follows.

A stochastic process x(t) is said to be first-order SC if its spectral mean is given by

(4.52)

That is, x(t) is an almost periodic function

(4.53)

with possibly random coefficients x_k with and deterministic frequencies .

Two jointly harmonizable processes x₁(t) and x₂(t) are said to be jointly SC if their spectral covariance function is given by

(4.54)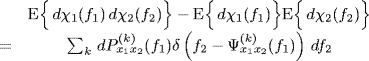

where does not contain jumps. If, in addition, has zero singular component, then is absolutely continuous and we have

(4.55)

Note that in the above definition, unlike the definition in Theorem 4.2.7, it is not assumed that the processes have no finite-strength additive sinewave components. In fact, since a covariance function is considered, the contributions of the Fourier transform of possible almost-periodic components present in the processes x₁(t) and x₂(t) are subtracted in the covariance definition.

From (4.49a) it follows that the Nth-order spectral moment function is given by the sum of the term (4.40) corresponding to the (only) partition with p = 1 in (4.49a) and the term corresponding to all other partitions with p ≥ 2. The former, containing only one Dirac delta, is refereed to as the pure Nth-order spectrally correlated component of the processes x₁, x_N. The latter is constituted by the sum of terms each containing the product of at least two Dirac deltas with different frequency variables. For this reason, the Nth-order spectral moment function is referred to as the impure Nth-order spectrally correlated component of the processes x₁, x_N. In fact, a nonzero is also due to terms with p ≥ 2 in (4.40), which arise from products of lower-than-Nth-order spectrally correlated components.

In contrast, the contribution of term (4.40) is not generated by products of lower-order spectrally correlated components. Moreover, according to (4.38), it can be obtained by depurating the spectral moment function (the term with p = 1 in (4.38)) from all possible products of lower-order spectrally correlated components.

Note that, in the special case of ACS processes, these considerations are the frequency-domain counterparts of the interpretation of the Nth-order temporal cumulant of an ACS signal as the pure additive finite-strength sinewave components that can be generated by the Nth-order lag-product of the signal (Gardner and Spooner 1994), (Spooner and Gardner 1994). However, the interpretation of pure and impure spectrally correlated components applies to a class of stochastic processes wider than that of the ACS process, namely the class of the SC processes.

4.2.4 Motivating Examples

Nonstationary (possibly jointly) SC processes that are not (possibly jointly) ACS can arise from linear not-almost-periodically time-variant transformations of ACS processes. For example, an ACS signal transmitted by a moving source and received by two stationary sensors, in the case of constant radial speed, gives rise to two signals that are jointly SC but are not jointly ACS (Allen and Hobbs 1992). Moreover, reverberation mechanisms generate coherency relationships ensemblewise between spectral components (Middleton 1967). In the following, examples where the SC model is appropriate to describe stochastic processes are discussed. Applications to communications, radar, and sonar are treated in Chapter 7.

4.2.4.1 Multipath Doppler Channel

Let us consider an ACS process passing through a multipath Doppler channel, that is, a linear time-variant system such that for the input complex-envelope signal x(t) the output complex-envelope y(t) is given by (Section 7.6.1)

(4.56)

where, for each path of the channel, a_k is the (possibly complex) scaling amplitude, d_k the delay, s_k the time-scale factor, and ν_k the frequency shift. Such a model is appropriate for describing the multipath channel when, for each path, the relative radial speeds between transmitter, receiver, and reflecting moving objects can be considered constant within the observation interval (Van Trees 1971) (Section 7.3). For example, in the case of moving transmitter and stationary receiver (e.g., transmitter is a mobile device and receiver is a base station), it results in and , where c is the medium propagation speed, is the relative radial speed for the kth-path, and f_c the carrier frequency of the real signals.

Accounting for the Fourier transform of (4.56), it can be shown that the Loève bifrequency spectrum of the output y(t) is given by (Section 7.7.2)

(4.57)

Furthermore, by substituting into (4.57) the expression (4.29) of the Loève bifrequency spectrum of an ACS process, it results in (Section 7.7.2)

(4.58)

That is, when an ACS process passes throughout a multipath Doppler channel, the output process is SC and the support in the bifrequency plane of its Loève bifrequency spectrum is constituted by lines with slopes (Figure 4.3).

In Section 7.5.1 it is shown that time-scale factors s_k can be considered unity in the argument of the complex envelope x(·) in (4.56) if the condition

(4.59)

is fulfilled, where B is input-signal bandwidth and T is the data-record length (see also (Van Trees 1971)). In such a case, the channel can be modelled as linear almost-periodically time variant and y(t) is ACS. However, in modern communication systems, wider and wider bandwidths are required to get higher and higher bit rates. Moreover, large data-record lengths are necessary for blind channel identification techniques or detection algorithms in highly noise-and interference-corrupted environments. That is, there are practical situations where the BT product does not satisfy (4.59) and, hence, the time-scale factors cannot be considered unity in the argument of the complex envelope x(·) in (4.56) so that the output process y(t) must be modelled as SC. For example, let us consider the direct-sequence spread-spectrum (DSSS) transmitted signal in a code-division multiple access (CDMA) system

(4.60)

where , with b_k { ± 1}, is the information-bit sequence, , with c_n { ± 1}, the spreading-code sequence, T_c the chip period, N_c the number of chip per bit, T_b = N_cT_c the bit period, and q(t) is a T_c-duration rectangular pulse. By assuming an approximate bandwidth B 1/T_c for x(t) in (4.60), condition (4.59) becomes

(4.61)

where N_b = T/T_b = T/(N_cT_c) is the number of processed bits in the data-record of length T. Therefore, if c 3 · 10⁸ m s⁻¹, =100 km h⁻¹, and N_c = 512, then (4.61) leads to N_b < 2 · 10⁴. That is, if the maximum number of processed bits exceeds few hundreds, then the received signal must be modelled as SC instead of as ACS.

Further situations where condition (4.59) is not satisfied and, hence, nonunit time-scale factors should be accounted for, can be encountered in sonar applications (Van Trees 1971, pp. 339–340), acoustic detection of aircrafts (Ferguson 1999), time-delay and Doppler estimation of wide-band signals (Jin et al. 1995), and ocean acoustic tomography (Munk et al. 1995).

4.2.4.2 MIMO Multipath Doppler Channel

Let us consider a multi-input multi-output (MIMO) system with sources x(t), = 1, …, L, and received signals y_m(t), m = 1, …, M, on a sensor array, where each link → m is constituted by a multipath Doppler channel:

(4.62)

In (4.62), for each path k of the → m link, a_km is the (possibly complex) scaling amplitude, d_km the delay, s_km the time-scale factor, and ν_km the frequency shift. K is the maximum number of paths over all links → m (some of the a_km are possibly zero).

If the sources are jointly ACS, that is

(4.63)

then the sensor signals are jointly SC, that is,

(4.64)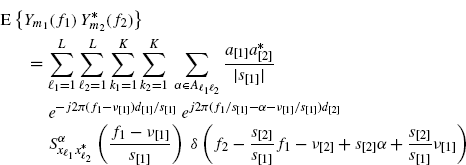

where, for notation simplicity, , , , and .

For K = 1, L = 1, and M = 2, we obtain as a special case the model considered in (Allen and Hobbs 1992).

4.2.4.3 SC Processes with Non-Linear Support Curves

Spectrally correlated stochastic processes with nonlinear functions can be obtained by feeding with ACS processes the “stationary linear time-varying systems” considered in (Claasen and Mecklenbräuker 1982) or considering frequency-warped wide-sense stationary or ACS processes. Furthermore, jointly SC processes with nonlinear functions are the input and output signals of the “stationary linear time-varying systems” or the linear time-variant systems described in (Franaszek 1967), (Franaszek and Liu 1967), (Liu and Franaszek 1969). Spectral analysis with nonuniform frequency spacing (Oppenheim et al. 1971), (Oppenheim and Johnson 1972), (Braccini and Oppenheim 1974), or spectral analysis by frequency warping techniques (von Schroeter 1999), (Makur and Mitra 2001), (Franz et al. 2003), can be shown to give rise to (jointly) SC processes with non linear support curves when the analyzed process is WSS or ACS (Section 4.13).

4.2.4.4 Fractional Brownian Motion

Definition 4.2.15 A real-valued stochastic process x(t) is said to be self-similar (Mandelbrot and Van Ness 1968) if

(4.65)

where = ^d denotes equality in distribution and H > 0 is the similarity exponent.

Fact 4.2.16 Equation (4.65) implies that

(4.66)

(4.67)

(4.68)

(4.69)

Definition 4.2.17 Fractional Brownian Motion (fBm). The fractional Brownian motion process B_H(t) is defined by (Mandelbrot and Van Ness 1968)

(4.70)

where B(t) is a zero-mean standard Brownian motion or Wiener process.

In (4.70), Γ(·) is the Gamma function (NIST 2010, eq. 5.2.1) and the parameter H (0, 1) is the Hurst parameter. Standard Brownian motion is obtained for H = 1/2. The process B_H(t) is a zero-mean nonstationary Gaussian process with stationary and self-similar increments, that is,

(4.71)

where the sense of equality is in distribution. Since B_H(t) is a zero-mean nonstationary Gaussian process, it is completely characterized by its autocorrelation function or bifrequency Loève spectrum.

Theorem 4.2.18 Autocorrelation of fBm (Flandrin 1989; Wornell 1993). Let x(t) = B_H(t). It results that

(4.72)

where

(4.73)

By substituting (4.72) into (1.16) (with (*) present), using the Fourier transform (Champeney 1990, pp. 137–138) (in the sense of distributions)

(4.74)

and accounting for the relationships Γ(z + 1) = zΓ(z) (NIST 2010, eq. 5.5.1) and Γ(z)Γ(1 − z) = π/sin (πz), (NIST 2010, eq. 5.5.3), the following result can be proved by taking λ = 2H + 1.

Theorem 4.2.19 Bifrequency Loève Spectrum of fBm (Øigård et al. 2006). Let x(t) = B_H(t). It results that

(4.75)

From Theorem 4.2.19 it follows that x(t) is a SC process with spectral masses concentrated on the three lines f₁ = f₂, f₁ = 0, f₂ = 0, and (4.75) turns out to be a special case of (4.23). Moreover, the power spectrum, defined as the Fourier transform of the time-averaged autocorrelation function (1.17) is given by the following result.

Corollary 4.2.20 Let x(t) = B_H(t). Its power spectrum is given by (Flandrin 1989)

(4.76)