Chapter 7. Phenomena of Diffusion
Learning Objectives
After completing this chapter, you will be able to:
Explain the kinetic theory interpretation of diffusion in gases as due to random molecular motion and the basic equations needed for prediction of binary diffusivity.
Calculate the value of diffusion coefficients in binary gas mixtures and describe the relationship between the diffusion coefficient and the temperature and pressure.
Outline the concepts behind Einstein’s model for diffusion of dilute solutes in liquids.
Identify the complexities associated with diffusion and concentration effects on diffusion coefficients, especially in liquids.
Associate the effects of pore structure and pore diameter with diffusivity of fluids in porous materials.
Describe the basics of solid-phase diffusion and the mechanisms underlying interstitial and substitutional diffusion.
Describe the basics of diffusion in polymeric solids, and explain the difference in diffusion in such solids compared to crystalline materials.
In this chapter, we look at the mechanisms of diffusion in gases, liquid, solids and porous solids. The molecular underpinnings of the diffusion mechanism are explained for all these cases, and some methods of a priori calculation of these coefficients are explored. We then address some complexities associated with diffusion, additional driving forces that can cause diffusion and the limitations of Fick’s law. The Stefan-Maxwell model is introduced for diffusion in multicomponent mixtures.
Diffusion can be considered to be the result of random motion of molecules, and this interpretation is especially suitable for gaseous systems. The kinetic theory of gases is a model based on random motion of molecules, and two key parameters in this model are the mean speed and the mean free path of the molecules. A model for the diffusion coefficients in a binary mixture of gases with similar sizes can therefore be developed based on this approach, and we discuss this model first. Modification of the kinetic theory to account for short-distance molecular repulsion, however, is a more realistic model. Development of a diffusion model based on this concept leads to some predictive models for binary diffusivity. The relevant equations are directly presented in this chapter without delving into the detailed molecular theory.
Adoption of a chemical potential gradient as a driving force provides an alternative platform for models of diffusion phenomena. The force due to the chemical potential gradient is assumed to be balanced by a frictional force, leading to an frictional interpretation for diffusion. We show how this provides the interpretation of multicomponent diffusion in gases, leading to the Stefan-Maxwell model for diffusion. The friction concept also leads to a model for diffusion of solutes in liquids which in turn provides the Einstein and Wilke-Chang model for diffusion in a liquid. In addition, we consider the effect of thermodynamic nonidealities on binary diffusion in a liquid mixture and the concept of activity correction to diffusivity.
We then move on to study solid–solid diffusion in crystalline solids and show the mechanisms and correlating equations for such a system. Diffusion of a fluid in a porous solid is also an important problem. In this context, we discuss how the diffusivity is affected by the pore structure, and we contrast diffusion in large-diameter pores with diffusion in small-diameter pores. A model for calculation of the effective diffusion coefficient in porous solids then follows. Diffusion in composite media and in polymeric solids is discussed as well. The chapter concludes with examples of some additional complex effects that influence diffusion.
7.1 Diffusion Coefficients in Gases
The kinetic theory of gases provides us with a framework to understand the phenomena of diffusion and offers some simple correlations for the diffusion coefficients for a gas phase binary mixture. This is discussed in Section 7.1.1. A frictional interpretation of the phenomena of diffusion is then presented in Section 7.1.2. Extension of the frictional concept to a multicomponent system leads to the Stefan-Maxwell model, which is introduced in Section 7.1.3.
7.1.1 Model Based on Kinetic Theory
The kinetic theory states that gas molecules are in a state of random motion. The physical properties of a gas that we observe on a continuum scale are associated with this random motion at the molecular level. For example, the pressure exerted by a gas may be viewed as the force exerted on the walls of a container by the gas molecules impinging on the wall and being reflected back. Similarly, the temperature of the gas, a continuum property, can be associated with the mean kinetic energy of molecular motion.
The kinetic theory interpretation of diffusion can be understood by looking at Figure 7.1. Molecules are in random motion and molecules from a plane at y – a and at y + a arrive at a plane a with equal probabilities. Here a is defined to be the distance at which molecules lose their identity from the point of their origin. This distance is related to the mean free path, as shown later in this section.
If the gas is pure, there is no net transport because the mass moving across from each side cancels out. In contrast, if there is a mass (or mole) fraction gradient, a net transport occurs from the region of higher concentration to the region of lower concentration. This relationship provides an interpretation of Fick’s law based on the kinetic theory concepts and a theory to predict the diffusion coefficients in binary gas mixtures. Let us walk through some of the mathematics that arises when there is a mass (or mole) fraction gradient in the system.
Diffusivity of A in a Medium of Similar Proprieties
Consider two planes separated by a distance 2a. The planes are located at y + a and y – a. Let us consider the molecules arriving at y from the top and bottom planes. The mean speed of the molecules is denoted as in random directions. The speed of a molecule as it passes across an area Δx Δz is taken as . Using this mean speed, the transport to the plane y from y – a and y + a can be calculated using the expressions for the convective flux:
Hence ωA(y – a) is the mass fraction of A in the mixture at y – a.
Similarly, mass coming from y + a and arriving at y is
If there is a mass fraction gradient, then a net transport occurs from a plane at higher concentration to a plane at lower concentration. The corresponding mass flux is the difference between the fluxes given by the previous two equations. Hence the net mass flux due to diffusion is
The difference in mass fractions can be related to the mass fraction gradient as follows:
Hence flux at y is
This suggests that the net flux is proportional to the mass fraction gradient and can be modeled by a Fick’s law type of equation:
The parameter may be defined as the diffusion coefficient of A in a medium with similar molecular properties:
The parameter a represents the distance between two collisions in the normal direction. From kinetic theory, this is related to λ as the mean free path:
a = (2/3) λ
Hence the diffusion coefficient is related to the mean free path and mean molecular speed as follows:
The following additional results from the kinetic theory can now be used. The average velocity is given as
while the mean free path is given as
Here κ is the Boltzmann constant, 1.38 × 10–23 J/K; m is the mass of the molecule; d is defined as the diameter of the molecule treated as a rigid sphere; and n is the number concentration, in units of molecules/m3.
We can now use ideal gas law to express n (number of molecules per unit volume) in terms of pressure, P, and temperature, T:
P = nκT
Hence the mean free path can also be expressed as
Using these relations for and λ in Equation 7.2, we get the following expression for the diffusion coefficient for gases with similar properties, which is also called the self-diffusion coefficient:
Equation 7.6 is based on many approximations but nevertheless predicts the pressure dependency correctly. The diffusion coefficient is seen to be inversely proportional to the total pressure of the gas. The temperature dependency is predicted somewhat less approximately. The equation indicates that the diffusivity is proportional to T1.5, but experimental data indicate that the exponent is actually closer to 1.75.
Diffusivity of A in a Medium of a Second Gas B
Development of the formula for DAB based on rigid sphere theory for two gases A and B with unequal molecular diameters and unequal molecular weights is more complex. Here, we will simply state the parameters needed and the final formula from other sources.
The extension of Equation 7.6 is based on a model in which molecules attract each other in general, but at short distances repel each other. Thus the assumption of molecules hitting each other (classical kinetic theory) is not correct because at short distances they repel each other. The basic kinetic theory was modified and corrected to account for this phenomenon by Chapman and Enskog.
Chapman and Enskog Model
The key modification in this model is the inclusion of the potential energy of the interacting molecules’ collisions. The intermolecular potential energy has the functionality shown in Figure 7.2 as a function of the distance of separation between the molecules.
The potential energy distribution is not exactly known but can be approximated by the 6-12 function, which is a good model for nonpolar molecules:
This function was introduced by Lennard-Jones (1924). Here σ is the effective diameter of the molecules and has a value close to the molecular diameter d in the earlier version of the kinetic theory, but not exactly the same. The second parameter, ∊, is the minimum potential energy value.
The values for σ are tabulated for many gases in many books, and values for some common gases are shown in Table 7.1. More extensive data are available in the book by Reid et al. (1977). In the absence of data, the value of σ can be calculated as an approximation from the critical properties data as follows:
Table 7.1 Lennard-Jones Constants for Some Gaseous Species
Gas |
Air |
CO2 |
Hydrogen |
Ethane |
Methane |
σ in ∘ A |
3.617 |
3.996 |
2.968 |
4.388 |
3.780 |
∊/κ in K |
97 |
190 |
33.3 |
232 |
154 |
σ = 2.44(Tc/PC)1/3
Similarly, the values of ∊ are tabulated for many substances but, as a quick approximation, can be determined based on the properties of the fluid at the critical point as follows:
∊/κ = 0.77TC
The units here are K for ∊/κ and A° for σ. The critical pressure is in atm.
Thus, the two parameters σ and ∊/κ for each of the gases in the binary pair were introduced into the molecular transport model, and the transport properties were predicted using this model in the work of Chapman and Enskog. Details are beyond the scope of this book, but the key result for the diffusion coefficient is
Here P is the total pressure in atm and DAB is in m2/s. Molecular weights are in g/mol here, rather than in kg/mol.
Two molecular-level parameters are needed to calculate the diffusivity using this formula. The first parameter σAB is taken as the average of the individual species values:
σAB = (σA + σB)/2
The second parameter ΩD,AB is the collision integral for diffusivity. For rigid spheres, the values are unity. The values for many gas pairs are tabulated in the literature (see, for instance, Bird, Stewart, and Lightfoot (1962)). This parameter is usually correlated with an energy parameter ∊AB or the equivalent temperature parameter ∊AB/κ. This is taken as the geometric mean of the individual energy parameters:
The collision integral ΩD, in turn, is correlated with a function of a dimensionless temperature, Θ, defined as T/(∊AB/κ):
The calculation of the diffusivity in binary gas mixture is shown in Example 7.1.
Example 7.1 Binary Diffusivity Calculation
Calculate the binary pair diffusivity of the methane–ethane pair at 293 K and 1 atm pressure.
Solution
The collision cross-sections for each species from Table 7.1 are as follows:
σA = 3.780° A and σB = 4.388° A
Hence σAB on average = (3.780 + 4.388)/2 = 4.084° A
Energy parameters from Table 7.1 for each species:
∊A/κ = 145K and ∊B/κT = 232K
The average energy parameter is the geometric mean average of the ∊ values and is calculated as .
The dimensionless temperature Θ is the actual temperature divided by the above value for the energy parameter = 293/183.41 = 1.5975.
The collision integral can then be calculated using Equation 7.9 using the above value for Θ. Its value is found to be ΩD = 1.168.
All of the quantities needed for the Chapman-Enskog equation (Equation 7.8) are now known. The diffusion coefficient is calculated by direct substitution as 0.1421 cm2/s. This is within 5% of the experimental value quoted in Reid, Prausnitz, and Sherwood (1977).
The MATLAB snippet shown in Listing 7.1 may be useful to perform these calculations since they are lengthy. The needed parameters for the gas pairs have to be entered as input to the program.
Listing 7.1 Binary Diffusion Coefficient Calculation
% Binary diffusivity in a gas mixutre.
sigmaAB = (sigmaA+ sigmaB)/2.
ebyK = (ebykA * ebykB)^0.5
% dimensionless temperature for collision integral calculations
tstar = T/ebyK
% Equation 7.9
Colli = 1.06036/tstar^0.15610 + 0.193/exp(0.47635 * tstar) ...
+ 1.03587/exp(1.52996 * tstar)+ 1.76474/exp(3.89411 * tstar)
% Equation 7.8 D in m^2/s
D_AB = 1.8583E –07 * (T^3 *(1/MA + 1/MB))^(1/2) ...
/P/sigmaAB^2/ Colli
Correlation of Fuller et al. for Diffusivity
An empirical model developed by Fuller et al. (1966) is also useful to predict diffusion coefficients:
Note that the format of the Chapman-Enskog correlation is retained here except for two changes:
Temperature dependency is changed to have an exponent of 1.75, which is closer to experimental values, and the collision integral is not used.
The sigma parameter is replaced by the cube root of a volume parameter, the diffusion volume. This in turn is calculated as the contribution of the atoms constituting the molecules. Diffusion volume for each molecule is obtained as a summation of the groups comprising the molecules. Values for many atoms are tabulated and some illustrative values are shown in Table 7.2.
Table 7.2 Group Contribution of Atoms for Diffusion Volume Calculation
Group
C
H
O
N
Cl
S
Aromatic ring
Contribution
16.5
1.98
5.48
5.169
19.5
17.0
–20.2
Values for some simple molecules are also available and are shown in Table 7.3. These values can be directly used for such cases; that is, summation over the atoms making up the molecules is not needed.
Table 7.3 Diffusion Volume for Some Common Molecules
Molecule |
Hydrogen |
Helium |
Oxygen |
Air |
CO2 |
CO |
Contribution |
7.02 |
2.88 |
17.9 |
16.6 |
26/9 |
22.8 |
Example 7.2 illustrates the use of the Fuller et al. correlation.
Example 7.2 Diffusivity by Fuller et al. Method
Find the diffusion coefficient of the methane–ethane pair at 1 atm and 273 K using Fuller et al.’s correlation.
Solution
Let 1 = CH4. The molar volume for methane is calculated by summing the contributions of the atoms that make up the molecules: 1C + 4H = 16.5 + 4 × 1.98 = 24.42
Let 2 = C2H6. The molar volume for ethane is calculated as 2C + 6H = 2 × 16.5 + 6 × 1.98 = 44.88.
The pressure P needed in units; of P = 1 atm. The temperature is T = 298 K.
The molecular weights are MA = 16 and MB = 30, in units of g/mol as needed in the correlation.
Substituting all the quantities into Equation 7.10, we find the diffusivity for this binary pair is D = 0.1542 cm2/s.
Diffusion at high pressure is important in many applications. Such measurements are often difficult, with only atmospheric pressure values being easily measured. In such cases, the relation D ∝ 1/P is applied and the atmospheric values are scaled accordingly.
7.1.2 Frictional Interpretation
A second phenomenological model for diffusion is based on the understanding that the diffusion rate is related to the frictional interaction between the diffusing species. This interpretation is useful for modeling diffusion in multicomponent systems, as shown in the next subsection. It is also useful for a first-level model of diffusion of a dilute solute in a liquid, which is discussed in the next section.
A frictional force is assumed to exist at the molecular level due to relative motion of A with respect to B (or vice versa). This frictional force per mole of A (1) acting on A exerted by B (2) is represented as
F = y2f12(v1 – v2)
where f12 is a friction coefficient parameter.
The velocities can be related to the diffusion fluxes:
A similar expression holds for species 2:
Therefore the velocity of species 1 with respect to species 2 is
Hence the frictional force is represented as
This expression for force is rearranged as
The frictional force is assumed to be balanced by a driving force. For the diffusion process, the force can be identified as the negative gradient of the chemical potential per mole. Thus
Figure 7.3 is a schematic representation of the balance of the two forces acting on a diffusing molecule.
For ideal systems
Equating the two expressions for F and with some slight rearranging, we obtain
Fick’s law for a binary system can be rearranged (after some algebra) to an “inverted” form:
This suggests that the friction coefficient can be replaced by diffusivity, with the latter defined as follows:
This provides a frictional interpretation of the diffusion coefficient. Diffusivity is inversely proportional to the friction coefficient. The extension of this concept provides a model for diffusion in multicomponent systems—namely, the Stefan-Maxwell model discussed in Section 7.1.3.
The reciprocal of the frictional resistance is referred to as mobility μm. Hence the following relation holds between mobility and diffusivity:
Equation 7.17 is known as the Einstein equation.
7.1.3 Multicomponent Diffusion
The frictional force on species 1 is calculated as an additive contribution to the friction due to all other species (2,3, . . .) present in the mixture:
The frictional resistance f1j can be related to each binary pair diffusivity as per Equation 7.16. Using this relation, we obtain
The left side of this equation is equal to –∇y1/y1 as per Equation 7.14 for the ideal gas. On the right side of the equation, the relative velocity of species 1 can be related to the diffusion fluxes as per Equation 7.11. Use of these relations then leads to following equation (known as the Stefan-Maxwell model) which is useful for ideal gas mixtures:
where ns is the number of components and Dij is the binary pair diffusivity in the gas phase. (Note: Summation for j = i cancels out and is not needed.) This equation can also be written in terms of the combined flux since
Ji = Ni – yiNt
The resulting equation is
This is another version of the Stefan-Maxwell equation. Equation 7.19 relates the fluxes Ni to the concentration gradients as expected from a constitutive model. Note that the fluxes here are implicit; they are not provided directly as a function of concentration gradients and have to solved as a part of the solution procedure together with the species mass balance equations. Hence the solution procedure is more involved (and is taken up in more detail in Chapter 15).
A further complexity is that the fluxes are all coupled, which is evident from the examination of the Stefan-Maxwell equation.
The concentration gradient of any particular species is a function of the fluxes of all the components present in the system.
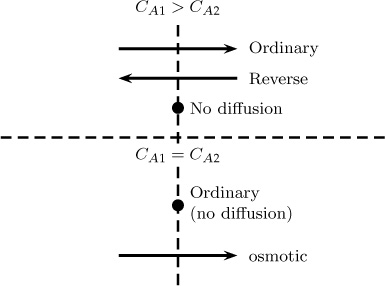
Some interesting and unexpected effects can arise in multicomponent systems as a result of this coupling. These effects, which are not seen in ordinary diffusion in binary systems, are briefly discussed here:
Reverse diffusion: A species may diffuse in a direction opposite to its concentration gradient.
Osmotic diffusion: Species may diffuse even though the concentration gradient is zero.
Barrier diffusion: Species may not diffuse even though there is a favorable concentration gradient.
Figure 7.4 depicts these complex effects.
These pathological cases arise mainly when the binary pair values are vastly different—for example, in a ternary mixture of hydrogen, air, and a heavy hydrocarbon such as heptane.
Example 7.3 applies the Stefan-Maxwell equation to a binary mixture.
Example 7.3 Stefan-Maxwell Model for a Binary Mixture with UMD
Gas A diffuses into an inert gas B. Apply the Stefan-Maxwell model to derive an expression for the flux of A. Assume no forced flow.
Solution
We use Equation 7.19 as the constitutive model for species A. In this case, ns = 2.
Equation 7.20 cannot be applied to species B, because ∇yA = –ΔyB and, therefore, no independent equation is generated. Hence we need a determinancy condition. In this case we have UMD and NB = 0. Also yB = 1 – yA.
Using this information and rearranging, we get
which is the model for flux in this case. Equation 7.21 was derived by starting with the version of Fick’s law given earlier and adding the convection contribution.
Extension of these equations to the multicomponent case and their solution are taken up in Chapter 15.
7.2 Diffusion Coefficients in Liquids
Because molecules are tightly packed in liquids, the kinetic theory approach of random collisions is not very appropriate for this form of matter. The mechanistic model for diffusion in a liquid is the so-called jump model, which the solute jumps from a vacant site to another vacant site. This model, which is shown schematically in Figure 7.5, is referred to as the Eyring theory. This model is more suitable for diffusion in solids, a topic discussed in Section 7.4.
A second theory applicable to liquids is the hydrodynamic theory, which states that the diffusivity is proportional to the mobility of the solute. In this model, the movement of the solute is treated as a sphere moving in an infinite pool of liquid with viscosity μL. The frictional interpretation of diffusion discussed in Section 7.1.2 is used here. Some remarks from that section are repeated here for ease of reading.
The force needed to move a particle with a velocity of vA (relative to B) is given, in general, by
F = fvA
where f is the coefficient of friction and vA is the terminal velocity of A.
For the diffusion process, the force can be identified as the negative of the gradient of the chemical potential per mole. Thus
F = –∇μA
The model and the balance of forces on a diffusing solute are illustrated in Figure 7.6.
The balance of the forces is represented in terms of the gradient of the chemical potential as
–∇μA = fuA
From the flux considerations, the relative velocity of motion of A is given as:
Hence
The term 1/f is identified as DA/RgT . In turn, the preceding expression can be rearranged to
Equation 7.22 shows that the gradient of the chemical potential is more appropriately considered the driving force for mass transfer, rather than the mole fraction gradient used in the traditional Fick’s law.
For ideal systems, this expression can be shown to be the same as Fick’s law. This follows from the definition of the chemical potential. The following relation from basic thermodynamics holds:
Taking the derivative to get the gradient of the chemical potential, we get
Substituting in Equation 7.22, we obtain
JA = –CDA∇xA
which is Fick’s law for an ideal mixture of liquids. The more general expression given by Equation 7.22 then provides an extension for diffusion in non-ideal systems. Moreover, the frictional interpretation provides a link to the molecular-level interpretation for diffusion and leads to a methodology to predict the diffusion coefficient. These two effects are explored in detail in the following sections.
7.2.1 Stokes-Einstein Model
The frictional resistance and the diffusivity are related as
where f is the frictional coefficient based on the number of moles of A. For the molecular model, it is more useful to write this relation as follows:
where f12 is the force per molecule. Note that κ = Rg/Navg has been used here to get from one form to the other.
At this point we use concepts from the fluid dynamics of slow flow, also called Stokes flow. The velocity of motion on a spherical particle in a liquid under slow flow conditions is related to the force F acting on the particle, and this relation is known as Stokes law:
where rA is the solute radius. Hence 6πμLrA can be identified as the friction coefficient f12.
Note: μL is the viscosity of the liquid medium (as indicated by the subscript L) and should not be confused with chemical potential.
Using the expression for f12 from Stokes law (Equation 7.25), we obtain
Equation 7.27 is the Stokes-Einstein equation, which is widely used as a starting model for liquid-phase diffusivity predictions. Predictions made using Equation 7.27 are fairly accurate under the conditions used in the model derivation—namely, a small rigid sphere (solute) moving in a continuum (solvent). Hence the model is representative of experiments in which the solute radius to solvent radius ratio is smaller than 5. For solute molecules with complex structure, a correction factor is often applied and a modified equation used. Nevertheless, a key result that emerges from Equation 7.27 is that
which fits the data for a large class of molecules. Indeed, this relation may hold even with molecules for which the Stokes-Einstein description may not be a good fit, such as nonspherical molecules and long-chain proteins.
7.2.2 Wilke-Chang Equation
An extension to the Stokes-Einstein equation is the Wilke-Chang equation:
where is the molar volume of the solute A (in cm3/mol) and MS is the molecular weight of the solvent (in g/mol). Also the viscosity, μL, is in centipoise which is equivalent to 0.001 Pa ˙ s, the S.I. unit for viscosity. The calculated value of D is given in units of m2/s here.
The empirical parameter, ø, in the preceding equation is known as the association parameter. It has a value of 1 for most organic solvents, 1.9 for methanol, 1.5 for ethanol, and 2.6 for water. Note that the equation has a form similar to that of the Stokes-Einstein equation (DAμL/T is a constant), and the dependencies of the temperature and the liquid viscosity are identical. The equation is not very accurate for concentrated systems, as the diffusion coefficient varies strongly with concentration. An activity correction is usually applied in such cases, as discussed in the Section 7.3.
The data for molar volume have been tabulated for many compounds, and some are provided in Table 7.4.
Table 7.4 Molar Volume for Some Common Species in Liquid Phase
Solute |
Hydrogen |
Oxygen |
CO2 |
NH3 |
Water |
, cm3/mol |
14.3 |
5.6 |
34.0 |
25.8 |
18.9 |
In the absence of such data, the following correlation developed by Tyn and Calus (1975) can be used:
where Vc is the critical volume of the solute in cm3/gmol .
Group contribution methods are also available to calculate this parameter, as discussed by Le Bas (1915). In this method, atomic volume increments are added together as per the molecular formula to obtain the molecular volume. The use of Wilke-Chang equation is shown in Example 7.4.
Example 7.4 Diffusion Coefficient in Liquids
Calculate the diffusivity of ethanol in water at a temperature of 298 K. Ethanol is present in small concentration.
Solution
Since ethanol is present in small concentration, it is treated as the solute and water is considered to be the solvent. The density of ethanol is 0.8 g/cm3 Hence the molar volume of ethanol is MAρA = 46 g/mol/0.8 g/ cm3 = 57.5 cm3/mol.
The viscosity of water is to be used in the Wilke-Chang equation because water is in excess and treated as the solvent. The value is μL = 9 × 10–4 Pa s.
We need to get this value in centipoise (c.p.). The conversion factor is 1000 c.p./Pa s. Hence μ (centipoise) = 0.9 c.p.
Molecular weight of solvent (water) is 18 gm/gmol.
Association factor, ø, is equal to 2.6.
Substituting in the Wilke-Chang equation, we get the diffusion coefficient: DA = 1.47 × 10–9 m2/s. Since ethanol was considered the solute, this is the value for a dilute solution of ethanol in water.
The Wilke-Chang correlation is suitable only for dilute concentrations of the solute. One consequence is that the binary diffusivity in an A-lean system (denoted here as DA) is not the same as the binary pair diffusivity in an A-rich system (denoted as DB here). This is because the environment (solvent) seen in an A-lean system (full of B) is different from that in an A-rich system (full of A). The values DA and DB are referred to as infinite dilution values.
For concentrated solutions, the following Vignes (1966) equation is often useful:
where DA is the diffusion coefficient of A in a B-rich mixture and DB is the diffusion coefficient of B in an A-rich mixture, with x being the mole fraction as usual. This relation can be viewed as logarithmic averaging of the two endpoint values.
An alternative way is to take the simple linear average:
In both cases, we find the diffusion coefficient is concentration dependent.
Having discussed some predictive methods for liquid-phase diffusivity, we now look at the case of non-ideal liquid mixtures, for which where a thermodynamic correction is needed.
7.3 Non-Ideal Liquids
Note: This section may be omitted on first reading.
The chemical potential gradient can be considered to be the driving force for diffusion rather than the concentration gradients. This leads to a modified form of Fick’s law that includes a correction factor known as the activity correction. The details are shown next.
7.3.1 Activity Correction Factor
The chemical potential can be represented as a function of the activity of species A:
The gradient for the chemical potential can be written as
In these equations, aA is the activity of species A in the mixture; xA is the mole fraction as usual. Using the expression for ∇μA in Equation 7.22, the Fick’s law type of model takes the following form:
For an ideal solution, the term d ln aA/d ln yA is equal to 1; hence Fick’s law holds in the form stated earlier. For non-ideal solutions, Equation 7.32 may be written in a form analogous to Fick’s law:
where D˚AB is the representative observed diffusion coefficient, which becomes equal to
Also aA = γAxA, where γA is the activity coefficient of A. Hence
Using this definition in Equation 7.34, we find
The term in the square brackets is called the (thermodynamic) activity correction factor.
The term DAB on the right side of the equation is also a function of concentration, since it should be some average of the infinite solution values (see Equation 7.28 or 7.29). Using Equation 7.29 and combining it with the previous equation leads to the the Darken relation:
This relation is commonly used to interpret and model diffusion in liquids.
Note: In many design applications, these complexities are ignored and absorbed in other fitting parameters. In other words, a fitted value of diffusion coefficient is used. Nevertheless, one has to bear these considerations in mind for more accurate modeling of mass transport in liquid–liquid systems.
7.3.2 Activity Coefficient Models
To incorporate the thermodynamic correction, the activity has to be fitted by a thermodynamic relation. A brief discussion of the models for the activity coefficient is useful here, although the detailed study of this topic is deferred to texts in thermodynamics. A number of models are available for this purpose, such as the Margules equation (the simplest), the van Laar equation, the Wilson equation, the NRTL three-constant model, and the UNIQUAC model.
In general, the activity coefficient is related to the excess free energy as follows:
The excess free energy is given by various models for non-ideal behavior due to differences in molar sizes, intermolecular forces, degree of hydrogen bonding, and other factors. These details are given in thermodynamic books. For binary systems, the Redlich-Kister equation is often used:
where A, B, and C are fitted parameters.
The simplest model for γ is the obtained by keeping only the first term, which leads to the one-parameter Margules equation. This produces the following expression for the activity coefficient:
The model presents a symmetric variation of the activity coefficient that is rarely observed. Thus this model is not suitable for thermodynamic correction for certain ranges of A. For example, the diffusion coefficient can become negative for certain range of mole fractions if the parameter A is greater than 2.
A two-parameter model is often used in which A is replaced by a linear function of the mole fraction:
ln γA = (1 – xA)2[A12 + 2xA(A21 – A12)]
This change is often sufficient to incorporate the effect of non-idealities on the prediction of the diffusivity. A more detailed NRTL model using three parameters may be more accurate, though. We now show the use of activity correction in Example 7.5.
Example 7.5 Activity Correction
Calculate the diffusion coefficient of acetone in water for a 50 mole % mixture.
Solution
We use the Wilke-Chang equation to find the infinite dilution values first. If acetone is treated as the solute, we get DA = 1.26 × 10–5 cm2/s. Similarly, if water is treated as the solute, we get DB = 4.68 × 10–5 cm2/s.
If no thermodynamic correction is applied, a linear interpolation of these values for xA = 0.5 leads to DAB = 2.97 × 10–5 cm2/s.
To apply the thermodynamic correction, ln γ vs xA was computed from the NRTL model. Taking the slope at xA = 0.5, we get d ln γA/d ln xA = –0.7. The thermodynamic correction is 1 + d ln γA/d ln xA = 0.3.
Hence the diffusion coefficient for a 50 mole % mixture is 0.3 × 2.97 × 10–5 = 0.8910 × 10–5 cm2/s.
The value will be 0.7285 × 10–5 cm2/s if the Vignes equation (Equation 7.28) is used, followed by the thermodynamic correction.
7.4 Solid–Solid Diffusion
In this section, we discuss diffusion in crystalline solids. In this scenario, atoms are placed in a regular array and closely packed. Diffusion is obviously a slow process in such a case, and the effects are observed only at high temperatures. Two mechanisms of solid–solid diffusion are discussed in the following sections.
7.4.1 Vacancy Diffusion
In a crystalline solid, some of the lattice positions are unoccupied and referred to as vacancies. This phenomenon is illustrated in Figure 7.7. Diffusion of a solute or impurity atom is then visualized as a jump of the diffusing molecule to a vacancy in the solid. A theoretical model based on this depiction leads to the following equation for crystalline materials:
where Ro is the spacing between atoms, fv is the fraction of vacant sites in the crystal, and ω is the jump frequency.
7.4.2 Interstitial Diffusion
A second mechanism is the interstitial diffusion. In this case, the solute occupies an intersite of the substrate atoms and moves to an adjoining interstitial site. This mechanism is illustrated in Figure 7.8.
Interstitial diffusion is modeled as
D = D0 exp(–E/κT)
where E is the activation energy needed to jump to the adjacent site and D0 is the pre-exponential factor. The activation energy is usually measured in electron-volts (eV). Hence the Boltzmann constant κ is used in the exponential term; it is equal to 8.617 × 10–5eV/K.
Substitution diffusion is an activated process but requires a lattice vacancy to form or exist. This requires an extra activation energy, denoted as Ev. Thus substitution diffusion is modeled by including two activation parameters, E and Ev:
D = D0 exp(–(E + Ev)/κT)
Many dopants can exist in both interstitial and substitutional sites. The diffusion can then occur by both mechanisms. Although the substitutional concentration is usually larger than the interstitial concentration, the interstitial jump is much faster than the substitutional component. Consequently, the overall diffusion is often governed by interstitial concentration.
Concentration-dependent diffusion is often observed with dopants in silicon. A power law type of model is commonly used for these cases. More details are given by Ghandhi (1983) and Middleman (1993). The mechanisms can be complex, and these sources should be consulted for more details. A few examples are given here to give a feel for the values of diffusion of some dopants in silicon.
Boron in Silicon: The data at concentrations of boron less than 1019 atoms/cm3 are correlated by an Arrhenius type of model:
where κ = 8.62 × 10–5 eV/K. Note that the activation energy is usually reported in electron-volts in these systems, whereas the diffusivity is in cm2/s. For higher concentrations, diffusivity is a linear function of boron concentration.
Arsenic in Silicon: The arsenic diffusion follows a similar pattern with the following values:
Phosphorus in Silicon: Phosphorus diffusion follows a similar pattern, with the diffusion coefficient remaining constant at low concentrations. It then decreases with concentration first and subsequently increases at larger concentration levels.
Note: Diffusion of phosphorus induces an electric field, and the combined mechanism should consider the effect of migration due to the electric field. Details are given in the paper by Fair and Tsai (1997) and in some other sources (Middleman and Hochberg, 1993).
7.5 Diffusion of Fluids in Porous Solids
Diffusion of a fluid in a porous medium is important in several applications. For example, reactants have to diffuse into the pores of a catalyst so that the reaction can take place; the products then have to diffuse out. The observed rate of reaction is affected by the rate of diffusion. In turn, the calculation of the effective diffusion coefficient in a porous solid is required to design these reactors. A model commonly used to describe this phenomenon is discussed in this section. Obviously, this process needs some model for the porous media. Typically, the average porosity is used to characterize the media. First we examine the diffusion in a single straight cylindrical pore.
7.5.1 Single-Pore Gas Diffusion: Effect of Pore Size
Let us consider the case of diffusion in a gas-filled pore. Assume that the pore size can be described by assigning a pore diameter dp to it. The operative mechanisms are different in large pores and in small pores, as shown in Figure 7.9. For large-diameter pores, molecular gas–gas collision is the dominant mechanism and the diffusion can be modeled by the binary gas pair diffusivity DAB. Pore size is not important here. In contrast, for small-diameter pores, the molecules are likely to collide more with the walls of the pores rather than with each other. The diffusion is therefore a result of gas–wall collision and the phenomenon at work is known as Knudsen diffusion.
The criterion used to distinguish between the two mechanisms is comparison of the pore diameter, dp, to the mean free path of the gas molecules, λ. If dp << λ, the Knudsen diffusion is the main mode of diffusion. The diffusion coefficient for this case is modeled using concepts similar to those found in the kinetic theory of gases:
Here is the mean molecular velocity given earlier in Equation 7.3. The only difference between this equation and that from kinetic theory is that the mean free path λ is not used, but instead is replaced by dp, the pore diameter.
Using the expression for the mean velocity from kinetic theory and substituting some universal constants, we can derive the following equation from Equation 7.37 for the Kundsen diffusion coefficient:
The units are cm for dp g/mol for MA, and cm2/s for D.
A combined model is used for the overall diffusion:
where DK is the Knudsen diffusion coefficient (Equation 7.38) and DAB is the gas-phase (binary pair) diffusivity. For small pores, the first term on the right side of Equation 7.39 dominates, so the overall diffusion coefficient depends on the pore diameter. For large pores, the second term dominates, so the diffusion coefficient is not a function of the pore diameter. Example 7.6 provides an example of the calculation of diffusivity in a single pore.
Example 7.6 Diffusion in a Single Pore
Hydrogen is diffusing into a cylindrical pore filled with methane. The pore diameter is 10 μm. Find the diffusion coefficient in this pore. Determine the dominant mechanism for diffusion.
Solution
The Kundsen diffusion coefficient is calculated from Equation 7.38. The pore diameter in centimeters is to be used: dp = 10 × 10–4 cm. Also T = 900 K and M = 2 g/mol. The value calculated is 102 cm2/s.
To find the dominant mechanism, we find the bulk diffusion coefficient at 273 K when the value of DAB = 0.625 cm2/s. The temperature correction with an exponent of 1.75 is applied. We find DAB = 5.94 cm2/s at 900 K, a much smaller value than the Knudsen diffusion coefficient. Hence the process is controlled by bulk diffusion and the Knudsen diffusion does not contribute to the transport rate. Molecules hit each other rather than hitting the wall.
We can also calculate the mean speed as given earlier and use the relation (dp/3) times the mean speed to get the Knudsen diffusion coefficient. S.I. units are to be used here. The mean speed is 3096 m/s calculated using Equation 7.3. Correspondingly, the Knudsen diffusion coefficient is . The pore diameter in meters should be used here.
Pressure Buildup in Small Pores
Consider two gases A and B that are counter-diffusing in a narrow porous capillary under conditions where Knudsen diffusion is the dominant mechanism. The diffusion coefficients are not equal; they are inversely proportional to the square root of the molecular weight. As a result, the sum of the diffusion fluxes do not add up to zero. The mass balance constraint for EMD requires that the net flux should be zero, but this condition is not being satisfied due to the unequal diffusion coefficient values for species A and B. In such a case, there must be a compensating mechanism, and a pressure profile builds up in the capillary. The viscous flow due to the self-generated pressure profile then takes care of the mass balance requirement. Hence the effect of the pressure-driven viscous flow must be included for cases where the pore size is sufficiently small for Knudsen diffusion to be dominant and when the two diffusing species have significantly different molecular weights. The overall effect of the pressure profile is usually within 10%, as confirmed by Evans (1972), and is often neglected.
For liquid pores, there is no Kundsen diffusion since the mechanism of diffusion is not collision, but rather frictional flow. Nevertheless, liquid-filled pores of a small size exhibit the phenomenon known as hindered diffusion, which is discussed in the following section.
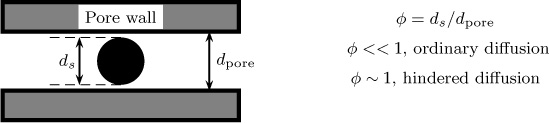
7.5.2 Liquid-Filled Pores: Hindered Diffusion
Consider diffusion of a molecule whose size is comparable to the size of the pores. The frictional resistance due to the pore wall should play a role, with the diffusivity being reduced compared to that for a larger-sized pore. This phenomenon is referred to as restricted diffusion or hindered diffusion. The extent of restriction depends on the size of the solute in comparison to the size of the pores. The possibility of hindered diffusion also opens up an engineering opportunity to design materials with controlled pore size so as to achieve selective diffusion of only the chosen solute.
A schematic of a small molecule diffusing in a small pore is shown in Figure 7.10.
The ratio of the solute diameter to the pore diameter is denoted by φ. The hindered diffusion becomes important if φ is close to 1 and is often modeled by introducing two correction factors, F1 and F2, that depend on φ. The first correction factor is simply a geometric factor known as the steric partition constant and is defined as follows:
F1(φ) = (1 – φ)2
The second correction factor is known as the hydrodynamic hindrance factor:
F2(φ) = 1 – 2.104φ + 2.09φ3 – 0.95φ5
The diffusion coefficient in small pores is obtained by multiplying the large pore value by F1F2. This is known as the Renken (1954) correction.
Hindered transport has been reviewed by Deen (1992). This paper is a useful reading for students who wish to explore this field further.
Adsorbed species can also move along the surface of the pore walls. This phenomenon, known as surface diffusion, and may operate in parallel with the pore diffusion.
7.5.3 Porous Catalysts: Effective Diffusivity
Porous catalysts cannot be modeled solely as diffusion in a single cylindrical pore since they constitute a network of interconnected pores. Instead, the pore size distribution plays an important role in the calculation of the effective diffusion coefficient.
A simple model is to define an effective diffusivity with the following equation:
De = Dpore∊p/τ
where ∊p is the catalyst (particle) porosity and τ is a tortuosity factor. The factor ∊p accounts for the reduced area for diffusion, while the factor τ is the correction for non-straight pores. These factors depend on the pore structure. Two common models for pore structure are shown in Figure 7.11. The first model assumes pores are composed of capillaries of various sizes connected in a random manner. The second model is applicable when the catalyst is formed by compaction of small, nonporous grains to form a porous pellet.
The pore diameter is often calculated by the following relation:
where ∊p is the particle porosity and Sp is the surface area of the pores per unit volume. The basis for this equation is the hydraulic radius concept, which is widely used in fluid mechanics for studying flow in noncircular channels. This concept applies to materials in which the pores show a unimodal distribution.
Example 7.7 shows some calculations for these quantities.
Example 7.7 Effective Diffusivity in a Porous Catalyst
A porous catalyst has a porosity of 0.60 and a surface area of 100 m2/g and is used for CO oxidation. The pellet has a density of 1.2 g/cm3. Find the effective diffusivity. Temperature is 400 K and pressure is 1 atm.
Solution
Surface area per unit volume is (100 m2/g)(1.2 g/cm3)/(10–6 m3/cm3) = 1.2 × 108 m2/m3.
The average pore diameter is calculated as 4 × 0.60/1.2 × 108 = 3.3 × 10–8 m. Using this, the Knudsen diffusion coefficient is calculated from Equation 7.38 as 3.66 × 10–6 m2/s.
The bulk gas diffusivity is 3.2 × 10–5 m2/s calculated from the Chapman-Enskog model given by Equation 7.8 for a CO–air mixture. Knudsen diffusion is the dominant mechanism and hence Dpore ≈ 3.66 × 10–6 m2/s.
Now we correct for the porosity and the tortuosity factors. Assuming a value of 2 for the tortuosity factor, we find De = Dpore∊p/τ = 3.66 × 10–6 × 0.2/2, which is equal to 1.06 × 10–6 m2/s.
The tortuosity factor is in the range of 2 to 3 for many catalysts with unimodel pore size distribution. Wakao and Smith (1964) suggest a value of 1/∊p could be used as an approximation in the absence of experimental measurements. Carniglia (1986) suggested the following equation for tortuosity:
where vp is the total pore volume, Δvp is the pore volume within an interval with an average pore diameter of dp, Sp is the BET surface area, and α is an exponent that depends on the pore shape. To use this equation, information is needed regarding the pore size distribution, which can be obtained from mercury porosimetry.
Bimodal Distribution of Pores
Many solids exhibit a macro–micro pore structure (a bimodal pore size distribution). For for such solids, the model proposed by Wakao-Smith (1964) is suitable. This model was developed by using the conceptual scheme shown in Figure 7.12. Model uses two average porosity values, ∊m for macro and ∊μ for micropores.
Figure 7.12 Illustration of the concepts leading to the Wakao-Smith model for solids with macro–micro pores.
The following equation can be derived based on this concept; it is shown directly without derivation here:
The pore scale diffusivity Dm and Dμ are estimated by the single-pore consideration given by Equation 7.39. This requires an average diameter for the macropores and micropores. These diameters reflect the surface area of the macropores and micropores. Note that Kundsen diffusion may be the controlling mechanism in micropore transport, whereas bulk diffusion may dominate the transport in macropores. Hence the pore-scale diffusivity values must be computed separately for the micropores and the macropores.
7.6 Heterogeneous Media
Transport in a heterogeneous medium is an important consideration in many applications. For example, a membrane may have a second material embedded within it.
Consider a material made of two types of matrices, with permeability Pc and Pd, respectively. Let ∊d be the volume fraction made of material d; 1 – ∊d is then the volume fraction of the second material. An effective permeability of the material Pe is to be computed. Here we discuss first two simple models: parallel and series arrangement of the laminate series. They provide two limiting cases to the general case (Figure 7.13).
For a series arrangement, the following equation—which is based on adding resistances in series—is used:
This can be rearranged to
The equation for the calculation of the permeability of parallel arrangement of laminates is
Pe = Pc(1 – ∊d) + Pd∊d
The predictions of the parallel and series modes bound the expected behavior of the composite matrix. Students studying heat transfer will be able to relate this to conduction in series versus in parallel.
An equation for the general case (in which the two materials are distributed in a random manner) was derived by Petropoulos (1985):
Here n is the shape parameter of the dispersed phase. The parallel arrangement corresponds to n = 0, a series arrangement to n = 1, and an embedded sphere (shown next) to n = 1/3.
In another useful model, one of the phases, denoted as d or the dispersed phase, is embedded in the matrix as solid spheres in a second phase, the continuous phase. The permeability of this composite can be calculated using an equation originally derived by Maxwell in 1873 in the context of electromagnetism to describe a composite dielectric medium:
A special case occurs when Pd is zero; it is applicable to the effective diffusivity in gas pores of a porous catalyst. In this special case:
Compare this relation with the expression for the effective diffusivity. The preceding equation predicts that the tortuosity factor is 3 – ∊c, which gives credence to the values of 2 to 3 for the tortuosity factor used in the reaction engineering literature.
7.7 Polymeric Membranes
Small permeates diffusing through a polymeric matrix are common in membrane separations. Examples are found in gas separation processes and discussed further in Chapter 27. Oxygen separation from air is one example.
In such gas separation processes, we require both a high rate of diffusion and selectivity for a particular gas. Solute (water) diffusion in polymeric food wrapping is an important application of this process, in which we need the polymer to act as a barrier. Transport of ions in a conducting polymeric matrix is important in electrochemistry. Oxygen permeability coefficients in polymers used to make hard and soft contact lenses are an important biomedical application, as is diffusion of drugs across a swollen polymeric capsule.
The glass transition temperature is an important parameter affecting the rate of diffusion. This is the temperature at which the polymer changes from a brittle solid structure to a glassy rubbery structure. If the glass transition temperature is exceeded, the diffusivity may change by an order of magnitude. Size of the permeate is an important factor as well. Swelling is another factor, as swelling typically increases the diffusion coefficient.
Recall that permeability is a product of diffusivity and solubility. Diffusivity increases with temperature, whereas solubility decreases under the same condition. The combined effect is that the permeability often shows a maximum with temperature.
Free volume theory is often used as a platform to predict diffusion. A free volume is a space that the solute molecule can occupy, similar to the holes observed in liquid diffusion. The free volume increases with an increase in temperature. The temperature at which the free volume increases rapidly is the glass transition temperature.
Neogi (1996) and Peppas and Meadows (1983) are good starting references that provide an introduction to the various theories that apply to polymeric membranes. These theories should be interpreted as a fitting tool rather than a complete predictive tool, since this research remains in its infancy. Many parameters can be adjusted to fit the data; however, the theoretical underpinnings in these models provide a solid platform for future development in this area. More coupling with molecular-level models can be expected in this field. The discussion provided in this section is rather brief and intended to give just an overview of this topic.
7.8 Other Complex Effects
In this section, we discuss a number of complex effects that can affect the rate of diffusion.
Dissociation Effects: Dissociation effects are of importance in liquid–liquid systems where a solute associates with the solvent molecules and the associated pair diffuses together. The solute may associate with itself (a type of dimer) and the diffusion may be controlled by that of the dimer rather than the original solute. Also the solute may dissociate and the two ions formed may then diffuse as a pair together with the diffusion of any undissociated solute. Diffusion of acetic acid in water is an example:
CH3COOH ⇌ CH3COO– + H+
The diffusion rate of acetic acid is therefore determined by the diffusion of the undissociated species CH3COOH and the diffusion of the ions, CH3COO–, and H+. Strong and complicated dependency on the concentration and the pH of the solution can be expected in many of these cases (since pH changes the extent of dissociation).
Facilitated Diffusion: Facilitated diffusion is a complexity usually associated with transport in membranes where a simultaneous chemical reaction is also taking place. A chemical reaction binds the diffusing species and enhances its transport. Life itself would not exist but for oxygen–hemoglobin interactions that proceed by facilitated diffusion. Similarly, many membranes (especially biological) have carriers, and the diffusing species binds to the carrier. Both the species and the carrier diffuse across the membrane , such that the transport is considered “facilitated.” This topic is studied in further detail in Chapter 22.
Active Diffusion: Active transport refers to diffusion against a concentration gradient at the expense of some work done on the system. A common example is the Na+-K+ pump, which is common across all living systems. This “pump” involves transport of sodium ions against a concentration gradient using the hydrolysis of ATP (adenosine triphosphate) as the energy source. The free energy released in the hydrolysis is used to overcome the difference in chemical potential of Na+, and a concentration difference on the order of 110 mol/m3 may exist for the steady state conditions across a cell membrane.
Thermal Diffusion: In thermal diffusion, a species diffuses due to the presence of a temperature effect. The additional mass flux resulting from thermal diffusion is usually modeled as
where kT is the thermal diffusion factor. In general for binary systems, species with larger weight move to the colder region, and vice versa.
Pressure Diffusion: In pressure diffusion, a species diffuses as a result of a pressure gradient. The contribution of pressure to diffusion is modeled as
Diffusion of Charged Species: Diffusion of charged species (e.g., ions) is important in systems such as electrochemical processes and fuel cells. The transport rate is augmented by adding the electrochemical potential as an additional driving force. Simultaneous solution of the diffusion equation and the electric field is needed for such problems. Chapter 16 provides a more detailed discussion of this subject.
Summary
The simple kinetic theory of gases provides a solid foundation to interpret diffusion in gases as well as a first-level model for predicting the diffusion coefficient. Diffusion is described as resulting from random molecular motion that brings species from a region of higher concentration to a region of lower concentration, consistent with Fick’s law.
Basic kinetic theory may be modified to account for short-range molecular repulsion, described by the Lennard-Jones model. Two molecular-level parameters for each species (σ and ∊) are needed in this model, and the model is in reasonable agreement with experiments for a large class of molecules. The Lennard-Jones model may not be suitable for long-chain molecules, which can not be represented by an effective collision cross-section. For such molecules with complex structure, molecular dynamics tools (not discussed in this text) are useful to predict the diffusion coefficients.
Another description of diffusion is based on the frictional interpretation. In this model, the driving force for diffusion is the gradient in chemical; this force is balanced by the frictional resistance created by molecule A squeezing past a solvent phase. The frictional resistance is, in turn, modeled as Stokes law for the liquid phase, which then leads to the Stokes-Einstein equation. This equation also forms the basis for the Wilke-Chang equation, which is widely used for calculating liquid diffusion coefficients.
For non-ideal liquid mixtures, the chemical potential depends on the activity coefficients. In turn, an activity correction factor is used in calculating the diffusion of non-ideal liquid mixtures. The Darken equation is widely used for this case.
Application of the frictional approach to a gaseous system leads to an inverted form of Fick’s law. This approach, when extended to a multicomponent system, leads to the Stefan-Maxwell model for multicomponent systems.
Additional effects due to solute–solvent molecular interactons are also important in diffusion in liquids. In such a setting, the nature of the species in solution (whether associated or dissociated, for example) can affect the rate of diffusion.
The Stefan-Maxwell model, in some situations, can cause strong coupling between the fluxes of various species. Complex effects such as reverse diffusion, osmotic diffusion, and barrier diffusion can arise due to these couplings.
Diffusivity of a fluid in a porous catalyst is an important parameter in modeling of fluid–solid reactions. For single straight pores, the diffusion can be retarded when the size of the solute is comparable to the pore diameter, a phenomenon known as Knudsen diffusion. For liquids, the frictional interpretation supports models for hindered diffusion, in which the diffusivity otherwise calculated for a larger pore is corrected for steric and hydrodynamic effects.
For industrial catalysts, the straight pore diffusivity value is corrected by porosity and divided by a tortousity factor. This model is applicable to materials with a unimodal pore distribution. For catalysts with a bimodal distribution, both the micropore porosity and the macropore porosity must be considered; the Wakao-Smith model is commonly used for this purpose.
Diffusivity of a solute in a second solid is important in microelectonic applications. The diffusing species can occupy the substitutional sites, the interstitial sites, or both. An activation energy type of model is used for these cases, especially to extrapolate the effects of temperature.
Diffusion in a heterogeneous medium depends on how the second phase (disperse phase) is distributed within the matrix. Simple models are based on either a parallel and series arrangement or an embedded sphere distribution of one phase in the second continuous phase. The relevant equations to calculate the overall effective permeability were given in this chapter; the Petropoulis equation is commonly used for a random distribution of the two phases.
For diffusion in a polymer, the glass transition temperature is an important property of the polymer. Th diffusion coefficient increases rapidly beyond this temperature. The free volume theory is widely used to model diffusion in polymeric systems.
Many other complex effects are often exhibited by diffusing systems. For example, reactive species present in the system can couple with the species being transported, leading to facilitated diffusion. Solute–solvent interactions can affect the diffusion. Additional diffusion can be caused by thermal and pressure gradients, although the contributions of these factors are small compared to the diffusion caused by the concentration gradient.
Review Questions
7.1 State the numerical value of the Boltzmann constant with units and show that it is equal to Rg/Nav.
7.2 How does the mean free path change with temperature and pressure?
7.3 How does the average speed of random molecular motion change with temperature and pressure?
7.4 What are the effects of temperature and pressure on binary diffusivity in a gas mixture?
7.5 Verify the dimensional consistency of Equation 7.6.
7.6 What is the effect of temperature on the diffusivity of a solute in a liquid?
7.7 Why and when is a thermodynamic correction needed to calculate the diffusion coefficient?
7.8 What is the Vignes relation?
7.9 What is the Darken equation and when is it used?
7.10 Can the parameter A be negative in the one-parameter Margules equation? If so, for which case?
7.11 What is Knudsen diffusion? When is it important?
7.12 What is the effect of temperature on the Knudsen diffusion coefficient? How does it compare to bulk (gas–gas) diffusion?
7.13 When does a pressure gradient build up in a porous solid?
7.14 What is hindered diffusion? When is it important?
7.15 What are the two factors to correct for hindered diffusion of a solute in a liquid-filled pore?
7.16 What is meant by the tortousity factor? State a simple formula to calculate this factor that can be used in the absence of experimental data.
7.17 How is the effective diffusion in a catalyst with a bimodal pore distribution calculated?
7.18 What is the glass transition temperature, and how does it affect diffusion in a polymer?
7.19 What is the effect of temperature on the diffusion coefficient of a gas in a polymeric solid?
7.20 What is facilitated diffusion?
7.21 What are thermal diffusion and pressure diffusion?
Problems
7.1 Maxwell-Boltzmann distribution and the average molecular speed. The speed of molecules according to kinetic theory is given by the Maxwell-Boltzmann distribution function f. Thus f(c)dc represents the probability that the speed c lies between c and c + dc, and the distribution function is modeled as
where α = m/(2κT).
Plot the function for CO2 at 300 K. Show that the area under the distribution function is unity, as would be expected for any probability distribution function.
Find the mean speed, defined as
7.2 Kinetic theory parameters for an oxygen molecule. Calculate the mass of an oxygen molecule and the average speed of the molecules are based on kinetic theory at a temperature of 273 K and 1 atm pressure. Compare this speed to the speed of sound in the medium. Compare this speed to the speed of Superman. Hint: Superman can reach the top of the St. Louis Arch 2.5 seconds. Also calculate the mean free path, assuming a molecular diameter of 3 °A (0.3 nm). Determine the self-diffusion coefficient of oxygen. Compare it with the oxygen–air binary diffusivity value of 1.75 × 10–5 m2/s.
7.3 Mean free path and mean speed. Calculate the mean free path of a nitrogen molecule at 1 atm, at a low vacuum (1000 Pa), and at a high vacuum (100 Pa). Assume a molecular diameter of 0.3 nm. The molecular Knudsden number is defined that a dimensionless number defined as the ratio of the molecular mean free path length to the molecular diameter. Find its value for nitrogen. Also calculate the mean molecular speed at 1 atm and a temperature of 300 K. How does it compare with the speed of sound?
7.4 Lennard-Jones parameter from critical properties. The critical temperature for CO2 is 304.25 K and the critical pressure is 7.35 MPa. Estimate the σ and ∊ parameters and compare them with the values given in Table 7.1.
7.5 Binary pair diffusivity in the gas phase. Estimate the diffusion coefficient of CO2 in air at 20° C and 1 atm pressure using the Chapman-Enskog equation. Compare the results using the Fuller correlation.
7.6 Stefan-Maxwell equation for a ternary gas mixture. Write out in detail the Stefan-Maxwell equation for a gas A diffusing in a mixture of B and C. Now consider the case in which only species A has a net non-zero combined flux— In other words, NB and NC are zero. Simplify the Stefan-Maxwll model for this case. Compare the result with the Wilke equation for a pseudo-binary diffusivity.
7.7 Liquid-phase diffusivity of a dissolved gas. Calculate the diffusion coefficient of dissolved CO2 in water at 300 K.
7.8 Liquid-phase diffusivity in infinite dilution conditions. Calculate the diffusion coefficient of ethanol in water (dilute solution with a large mole fraction of water) at 298 K. using the molar volume based on the density and the molar volume based on the group contribution method. The atomic increments are carbon = 14.8, hydrogen = 3.7, and oxygen = 7.4 (all in cm3/mol), as reported in Le Bas. Also calculate the diffusivity of water in ethanol (dilute solution with a large mole fraction of ethanol).
7.9 Liquid-phase diffusivity as a function of composition. Calculate and plot the diffusivity as a function of the mole fraction for an ethanol–water mixture using either the linear interpolation or the Vignes equation. Ignore the thermodynamic correction. Now find the activity coefficient of ethanol as a function of composition using thermodynamic data and correct the results for the diffusivity using the thermodynamic correction factor.
7.10 Diffusivity in an acetone–water mixture. Verify the calculations for the diffusion coefficient of acetone in water for a 50 mole % mixture, as shown in Example 7.5. Now find the values at various compositions and plot the diffusivity as a function of mole fraction of acetone.
7.11 One-parameter model for activity coefficient. Consider the simplest model for the activity coefficient:
Calculate γA and plot it as a function of the mole fraction of A for different values of A (A = 0, which is the ideal case; A = 1; A = 2 and 3). The correction becomes negative for certain value of A, which means the observed diffusion coefficient becomes negative! Provide an explanation for this outcome.
7.12 Use of Gibbs-Duhem equation. State the Gibbs-Duhem equation. Using this equation, show that the thermodynamic correction for diffusivity for species A is the same as that for B in a binary mixture. In other words, verify that the sum of the diffusion fluxes is zero at any specified mole fraction value. Also verify that DAB = DBA at a fixed concentration, although the values may be concentration dependent.
7.13 Diffusion in a straight pore. Calculate the value for silane diffusing in a 10-μm cylindrical pore at 900 K, which is representative of the deposition of solid silicon in thin tubes. Determine the dominant mechanism for diffusion in this case.
7.14 Hindered diffusion in a nanosized pore. Glucose is diffusing across a microporous membrane with pores of 2-nm diameter. The mean diameter of the glucose molecule is about 0.86 nm. Temperature is 300 K. Find the diffusion coefficient using the Stokes-Einstein equation. To what extent is the hindered diffusion correction important in this case?
7.15 Size exclusion–based separation. A protein solution is separated from water by allowing it to diffuse across a porous nanosize membrane. The size of the protein is 25 nm. Find the diameter of the membrane to have a steric partition coefficient of 0.64. If a second protein has a a size of 50 nm, find the relative exclusion of this protein in the membrane.
7.16 Effective diffusivity in a porous catalyst. Calculate the effective diffusivity of ethylene diffusing in hydrogen gas at 1 atm pressure at a temperature of 298 K given the following properties of the catalyst: porosity = 0.4; surface area = 100 m2/g; bulk density of the catalyst = 1.4 g/cm3.
7.17 Bimodal pore distribution. A porous catalyst has a bimodal distribution with porosity of 0.233 in the micropores and 0.492 in the macropores. The average pore radii values are 40 nm in the micropores and 2 μm in the macropores. Find the effective diffusivity for a methane–air mixture.
7.18 Diffusion in a composite matrix. A polymeric membrane is made of two material with permeability of 1 × 10–5 and 4 × 10–5, respectively. The second material is embedded in the first, with a distribution of 15%. Calculate the overall permeability assuming (a) a series arrangement, (b) a parallel arrangement, and (c) the second material embedded as small spheres in the first material.