Chapter 18. Mass Transfer with Reaction: Porous Catalysts

In industrial practice, reactions where a fluid species reacts over a porous solid catalyst is very common. The concentration of the reacting species may vary in the interior of the catalyst especially if the diffusion rate is low or if the reaction rate is rapid compared to diffusion. Thus the rate calculated on the basis of the external concentration may not be representative and an average rate that accounts for the concentration variation in the pores of the catalyst is needed in order to design industrial gas–solid catalyzed reactions. Hence mass transfer effects are of importance in design of catalytic gas–solid reactions. It is the goal of this chapter to examine the role of mass transfer in porous catalysts.

The chapter is organized in the following manner. First we show some industrially relevant examples and properties of common catalysts. Then the diffusion-reaction problem is analyzed for simple cases where diffusion is only in one coordinate direction. First-order and zero-order reactions are studied where analytical solutions are possible. Then we show how semi-analytical solutions can be obtained for nth-order reactions. The important concept of effectiveness factor, which is a measure of pore diffusional effects is introduced, and its relation to a key dimensionless parameter, the Thiele modulus, is discussed. Application of this relationship results in the correct interpretation of kinetic data measured from laboratory reactors and examples of this are presented.

Two computational tools for studying the effect of internal diffusion for nonlinear and multistep reactions are then discussed. Finally the effect of heat generation due to reaction is studied based on the analysis of simultaneous heat and mass transfer within the catalyst. Many complex effects such as multiple steady states, effectiveness factor larger than one, and so on, are observed in such systems and we show some examples of this behavior. Linking of the local model to the mesoscopic models for the gas phase is then shown with some examples. Overall, the chapter provides a solid fundamental background for further study of catalytic reaction engineering in detail.

• Sulfuric acid manufacture: The first step is in this process is the oxidation of sulfur dioxide over a vanadium pentaoxide catalyst. Worldwide production is on the order of 140 million tons.

• Ammonia production: Reaction of nitogen and hydrogen over iron gauze catalyst at high pressures is used to produce ammonia. This is the starting material for the fertilizer industry. This is also a large-scale process.

• Ethylene oxide production from ethylene: Ethylene and oxygen (air with 95 mole % of oxygen) are mixed in a ratio of 1:10 by weight and passed over a catalyst consisting of silver oxide deposited on an inert carrier such as corundum. Commercial processes operate under recycling conditions in a packed bed multitubular reactor. The reaction is highly exothermic and heat management and heat recovery are important (not addressed in this book). It can also lead to a side reaction of complete oxidation that needs to be minimized as well.

• Methanol synthesis from a CO and H₂ gas mixture over a Cu-based catalyst. Packed bed tubular reactors are commonly used.

• Maleic anhydride production by butene oxidation. Fluidized bed reactors are used since they provide a uniform temperature environment and facilitate control of the reactor temperature.

The catalysts are generally porous with a large internal area and the species diffuses into the pores and simultaneously interacts with the pore walls and undergoes a chemical reaction. The products counter-diffuse back to the bulk gas. The diffusion in the pores sets up a concentration gradient within the pellet and mass transfer models are used to calculate this. The rate of reaction is lowered (generally) due to this concentration gradient and a primary goal is to calculate this reduction factor, which is usually calculated as an effectiveness factor. The methodology and the results will now be studied. We first review some properties needed to characterize a given catalyst.

The internal surface area of the catalyst, S_i, is another important property and usually expressed on the basis of the mass of the catalyst. Most of the surface area is in the internal pores and hence surface area is a usually large, on the order of 1000 m²/g. This should not be confused with the external surface area, denoted as S_p, which for example is equal to 3/Rρ_b. This is external area per unit mass of the catalyst for a spherical particle of radius R.

The average pore radius of a catalyst is defined as

r¯pore=2VporeSi

Here V_pore is the pore volume per unit mass of the catalyst. There is usually a pore size distribution within the catalyst, which is characterized by a distribution function, f. Thus f(r)dr denotes the fraction of the pores in the pore radius range r and r + dr. The distribution can be unimodal, which represents a case where there are only pores near one size range. An average pore radius can be defined as the first moment of the distribution:

r¯p=∫0∞rf(r)dr

The distribution of pore sizes can be measured by mercury porosimetry, where Hg is forced into the pores under pressure. The pressure required is a measure of the radius of the pore, with the smaller pores requiring higher pressures for the mercury to penetrate.

Many catalysts have a bimodal distribution and consist of macropores and micropores. In such cases the distribution function shows two peaks, one at the average micropore diameter and one at the average macropore diameter. Correspondingly a micropore porosity and a macropore porosity can be defined. These properties are useful, for example, in the Wakao-Smith model to predict the internal diffusivity (see Chapter 7).

The model equations are simply truncated versions of the general equations of mass transfer and are known as the diffusion-reaction equations. For the steady state case the rate of diffusion balances the local rate of reaction and the model equation is of the form

where C_A is the concentration of the diffusing species in the pores of the catalyst and D_e is an effective diffusivity of the species A in the pores of the catalyst. One assumption here is that diffusion-induced convective flux term is neglected here. Also, the diffusivity is taken as a constant. The effective diffusivity can be calculated by the models described in Chapter 7.

A note on the basis used in the definition of the local rate of reaction R_A is in order. The local rate at any point within the catalyst is defined based on the local volume of the catalyst. This includes the solid and the pores and is treated as a volumetric or homogeneous source of mass. The actual reaction takes place by adsorption followed by reaction on the pore surface and these are lumped into a composite “homogeneous” type of rate based on the catalyst volume.

Rate is also defined in some sources based on the unit mass of the catalyst, per surface area of the catalyst, on the mass of active metal loaded on the surface of an inert support, and so on. All these are valid definitions as long as the basis is clearly stated. A proper conversion factor needs to be applied in order to base the rate based on these other definitions on the unit catalyst volume basis used in this chapter.

Solutions to the diffusion-reaction equation in complex shapes with 3-D models and mixed boundary conditions (Robin in some parts of the control surface and Dirichlet over the other area) are difficult and generally require numerical solutions. We examine here simple 1-D cases by taking simple geometries. These geometries are slab, long solid cylinder, and solid sphere, where the Laplacian can be represented as a function of one spatial coordinate. Examples of these were already introduced in Chapter 2 and should be revisited.

The boundary condition at the surface can be of the Dirichlet type, or the Robin type as discussed later. Also, the method of solution depends on the kinetics of the reaction. For zero and first-order kinetics, analytic solutions can be obtained. Zero-order reactions have to be given special consideration as shown later since the concentration can become zero at some point in the interior of the catalyst. Nonlinear kinetics can be solved semi-analytically by a method of p-substitution for simple slab geometry. More general cases involving multiple species or multiple reactions or simultaneous heat transfer effects are best handled with numerical methods. We will study some numerical tools in this chapter as well for some simple cases; these form the foundation for the solution of other complex cases.

For a first-order reaction R_A = –k₁C_A and the differential equation in Equation 18.1 can be represented for slab geometry as

The scaled concentration c_A is C_A/C_A,b, where C_A,b is the concentration in the bulk gas outside the catalyst while ξ is a dimensionless spatial location equal to x/L. The L is taken as half the thickness of the slab in order to take advantage of the symmetry for ease of solution. The distance x starts now from the center of the slab.

Using these variables the dimensionless representation is

The key dimensionless parameter appearing in the above dimensionless formulation is ϕ and is called the Thiele modulus. Thus the square of the Thiele modulus is defined as

The Thiele modulus (squared) can be interpreted as the ratio of the characteristic time for diffusion L²/D to the time for reaction 1/k. It can also be interpreted as the ratio of the relative rate of reaction to the rate of diffusion within the pores:

Thiele squared=diffusion timereaction time=reaction ratediffusion rate

The boundary condition at the plane of symmetry for slab is dc_A/dξ = 0. The plane of symmetry is taken at ξ equal to 0. This boundary condition is also applied at the center for the long cylinder and sphere as well.

The boundary condition at the surface ξ = 1 depends on whether external mass transfer effects are accounted for or not. We postulate the existence of a thin film or a boundary layer near the surface in accordance to film theory. This thin film offers all the resistance for gas transport from the bulk to the surface of the catalyst. A balance of fluxes at the surface can then be represented as

km(CA,b−CA,s)=De(dCAdx)x=L

where k_m is the external (gas film) mass transfer coefficient and the left-hand side above represents the mole of A transported from the gas to the surface. The right-hand side is the rate of diffusion into the catalyst surface. The dimensionless version of the condition is as follows and is of the third kind (Robin):

(dcAdξ)ξ=1=Bi[1−(cA)ξ=1]

where Bi for external mass transfer is defined as

Bi=kmLDe

The Biot number represents the ratio of the external transport rate to the internal transport rate and has the same significance as in heat transfer:

Biot number=externl mass transfer rateinternal diffusional rate

For large values of Bi we would expect the problem to reduce to the Dirichlet type (external transport rate would be large and therefore there is no external transport resistance). Hence if there are no transport resistances on the film near the catalyst then the Dirichlet condition c_A = 1 can be directly applied at ξ = 1, which simplifies the math. The parametric representation of the problem is then simpler and is represented as: c_A = c_A(ξ; ϕ).

cA=cosh(ϕξ)cosh(ϕ)

This was already shown in Section 2.4 for a similar problem of oxygen diffusion with reaction in a pool of liquid.

Effectiveness factor=actual ratemaximum rate

The maximum rate is the rate based on the external gas concentration. This is, of course, the same as the rate based on the surface concentration for large Bi. It is equal in this case to k₁C_As.

The actual rate can be calculated in two ways: by taking the local rate and integrating over the whole catalyst or by calculating the rate of transport into the catalyst at the surface by using Fick’s law.

In the first case we have to integrate the concentration profile while in the second case we need the derivative of the concentration profile at the surface (in order to apply Fick’s law here). Both cases lead to the same answer.

The effectiveness factor can be shown to be the same as the average rate of reaction in dimensionless units. The following expression can be easily derived:

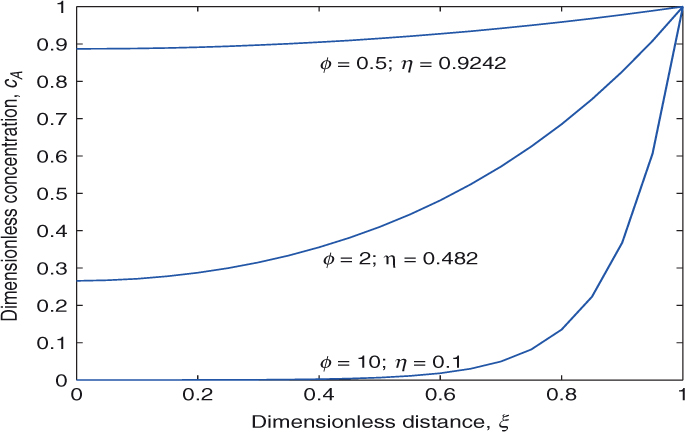
The concentration profiles are shown in Figure 18.1 together with illustrative values for the effectiveness factor. Note that the concentration profiles get steeper as the Thiele modulus is increased with a corresponding drop in the effectiveness factor. For example for ϕ = 10, it is hard for the reactant A to reach the interior of the catalyst, leading to an effectiveness of only 0.1.

The reader may wish to verify the algebra and also show that the Dirichlet limit is approached as Bi → 1. Such limiting cases should always be checked in general.

The effectiveness factor expression for the above case can be derived as

Here s = 1 the geometry parameter and ξ is the dimensionless parameter, r/R. Note that if s is set as zero the slab equation is recovered. Similarly if s = 2 the model for a sphere is obtained.

The previous differential equation for a cylinder is now the modified Bessel equation. This can be seen by expanding the Laplacian and rewriting the equation as

ξ2d2cAdξ2+ξdcAdξ−ξ2ϕ2cA=0

The general solution is

c_A = A₁I₀(ϕξ) + A₂K₀(ϕξ)

Students may wish to verify the general solution using MAPLE or the information given in advanced engineering mathematics textbooks such as Kreyzig (2010).

The constants of integration are readily found for a solid cylinder. The function K₀ goes to infinity as r → 0 and hence A₂ is set as zero so that the concentration remains finite at the center. The second constant is then fitted from the boundary condition at ξ = 1, which may be of the Dirichlet or Robin type. For the Dirichlet type (infinite Biot number) the solution is

cA=I0(ϕξ)I0(ϕ)

The effectiveness factor is the ratio of the actual rate to maximum rate. The actual rate is the integral of the local rate multiplied by the local volume:

Actual rate=∫0R2πrLk1CAdr

The maximum rate is

Maximum rate = πR²Lk₁C_A,s

L here is the length of the cylinder.

The ratio the two rates leads to the following expression in dimensionless version:

η=2∫01ξcAdξ

An alternative expression for the effectiveness factor is found from the flux crossing into the cylinder at the surface:

η=2ϕ2(dcAdξ)ξ=1

Students should verify that this will be the expression from flux considerations at the surface; both expressions will lead to the same final answer, which is

This is valid for large Biot numbers; that is, when the gas film transport is not rate limiting. The solution to the case of a finite Biot number is left as an exercise.

The effectiveness factor is given as

η=3∫01ξ2cAdξ

and the final result is

Example 18.1 shows an illustration of the drop in the concentration profile due to pore diffusion.

We define a characteristic length parameter (equivalent half-length of a slab catalyst) as

L_c = V_p/S_e

where V_P is the volume of the particle and S_e is the external surface for diffusion of the gas into the porous solid.

A Thiele modulus is then defined based on this length scale as

ϕ*=Lck1DA

irrespective of the actual shape of the catalyst; the slab equation is used for all the geometries as an approximation with the above-defined Thiele modulus:

η=tanh(ϕ*)ϕ*

Note that ϕ* for a cylinder is ϕ/2 (the length parameter is now R/2). Similarly it is ϕ/3 for sphere. The length parameter is R/3. A plot of the effectiveness factor for all three geometries is shown in Figure 18.2.

We find from this figure that the slab approximation is reasonable for all three geometries. The results for all three geometries get compacted with this modified (shape-normalized) Thiele modulus. The maximum error is on the order of 10% and is observed at an intermediate value of the Thiele modulus. The concept can be used for complex shapes; Example 18.2 shows one application.

At steady state the rate of external mass transfer is k_mS_e(C_A,b – C_As), which is also equal to the rate of reaction in the interior of the catalyst, V_pk₁C_A,s η. The latter can be also represented as VpR¯A, which is the measured rate. Hence

CA,b−CA,s=VpR¯AkmSe

If the rate is measured and the external mass transfer coefficient is measured independently or estimated from correlations we can find the concentration drop in the film from the previous equation. If the drop in the external film should be small relative to the bulk concentration, then the external mass transfer resistance can be neglected.

Note that the local rate of reaction is k₁C_A(x) per unit catalyst volume. As the concentration is changing within the slab, the rate is different at different points in the slab. What one would observe is an average rate, which can be calculated using the definition of η. Hence

−R¯A=k1CA,bη

Using the expression for η (for the slab model with no external resistance)

−R¯A=k1CA,btanhϕϕ

an apparent rate constant can be defined as the observed rate divided by the bulk concentration. This is observed to be

kapp=k1tanhϕϕ

which is not in general equal to the true rate constant k₁. This indicates that the measured value should be appropriately corrected for diffusional effects. Example 18.3 illustrates this.

Two limiting cases are worth noting:

• No pore resistance: This holds for low ϕ. The effectiveness factor = 1. The average rate, which is also the observed rate, is

  −R¯A=k1CA,b

  The apparent rate constant and true rate constants are the same. The true rate constant can therefore be directly estimated from the measured data in this case. Also note that the particle size has no effect. One way to check this is to take two relatively small particle sizes. The measured rate will be the same if there are no pore resistances due to diffusion.

• Strong diffusional resistance, which holds for high ϕ; Usually ϕ > 3 is taken as the criteria. Here we can show that η = 1/ϕ since the function tanh ϕ will now be one. Hence the measured rate would be

  −R¯A=CA,b(DeAk1L)(18.12)

  The apparent rate constant is now the bracketed term on the right-hand side. The rate is inversely proportional to the size of the catalyst. This is called the strong diffusional regime. A true rate constant cannot be directly obtained here but can be back-calculated if the effective diffusion coefficient is known or estimated. Example 18.3 illustrates the procedure.

The slab analysis proceeds as follows with the basic diffusion-reaction equation:

Ded2CAdx2−k0=0

where the production rate of A, R_A, has been replaced by minus k₀, the zero-order rate constant for the metabolic process. The boundary conditions are set as follows:

• At x = L, C_A = C_As, a prescribed or known surface concentration (Dirichlet case).

• At x = 0, the center of the slab, we use the no flux condition dC_A/dx = 0.

The dimensionless version of the previous equation can be easily derived as

Here ϕ02 is the square of the Thiele modulus for a zero-order reaction. This should be defined as

Note that the Thiele modulus depends on the surface concentration, unlike the case of a first-order reaction. This is true in general for any nonlinear kinetics.

The solution for the concentration profile (in dimensionless form) is very simple:

The center concentration is assumed to be above zero so that this equation can be applied.

The condition at which the center becomes zero or remains positive is then obtained from Equation 18.15 by setting ξ = 0 as

ϕ0≤2

For this case, there is no reactant starved zone in the interior of the catalyst. The rate of consumption of A per unit volume is k₀; this is independent of the concentration, as expected for a zero-order reaction. Hence the effectiveness factor is equal to one since the entire catalyst is exposed to the reactant as long as this condition is satisfied.

The solution for a larger Thiele modulus is studied next where a reactant starved region develops near the center of the catalyst.

cA=1−ϕ022(1−2λ)+ϕ022(ξ2−2ξλ)

The position λ is not known. Hence we impose an additional condition that the concentration c_A is also zero at x = λ. This provides the following condition for the calculation of λ:

λ=1−2ϕ02

Note that only the region to 1 is effective for a reaction. Hence the effectiveness factor is simply the length of the region and can be calculated as

The rate of consumption of A per unit volume is now k₀ η and turns out to be

This shows a square root dependency on the surface concentration. Thus a zero-order reaction appears as a half-order reaction due to the presence of diffusional effects.

This is a general effect and can be stated as follows:

A reaction of true order n appears as a reaction of (n + 1)/2 when strong pore diffusional resistances are present.

The concentration profiles for various ranges of the Thiele parameter are shown in Figure 18.3.

In Figure 18.3 three cases are shown. The first case is for ϕ₀ = 1 and represents the no starvation case; the concentration remains finite everywhere. The second case is for ϕ0=2. The concentration becomes zero at the center; this represents the onset of starvation. The effectiveness factor is one for both these cases. The third case is for ϕ₀ = 3 and represents a case of strong diffusional gradients. The concentration becomes zero at ξ = 0.53. The region from 0 to 0.53 is not effective for the reaction. The effectiveness factor is equal to 0.47, the width of the zone where the reactant concentration is non-zero.

Similar to a zero-order reaction, reactions with power law order less than one can exhibit a depleted zone near the center. The analysis of this problem was undertaken by Mehta and Aris in 1971 following the work of another earlier researcher and resurrected in 2011 by York et al. (2011). The mathematical method to find the critical Thiele modulus is examined in exercise problem 10.

We now move to a nonlinear nth-order reaction and illustrate a mathematical solution method for such problems for large values of the Thiele modulus. The corresponding result for the effectiveness factor is known as the asymptotic solution.

The order of the differential equation can be reduced by one by using the transformation p = dC_A/dx. (Hence the method of solution is called the p-substitution.) Noting that

we find that Equation 18.18 can be written as

This equation can be solved by separation of variables to get an expression for p, the concentration gradient:

or

The limits are set as follows. For flux the limits are set as 0 at the center and the unknown surface gradient p_s. For concentration the unknown center concentration and the known surface concentration are used.

Note that the center concentration is unknown but an expression can be derived in integral form upon a second integration. However, these details are not important in the asymptotic region, which applies for large values of the Thiele modulus. Here the concentration drops to nearly zero at some point in the interior of the catalyst. Thus we can set C_Ac ≈ 0 and use this in the above expression. The flux at the surface is then given as

Taking the square root with the positive sign (since the concentration is increasing with increase in x), we obtain an expression for the surface gradient:

The quantity entering the catalyst M˙A is given as

Correspondingly the average rate of reaction is obtained as

Using Equation 18.24 for p_s, the following expression is obtained for the average rate:

Note that this reduces to Equations 18.12 and 18.17 for first-order and zero-order reactions with n equal to 1 and 0, respectively.

η=−R¯Akn(CAs)n

Therefore the following expression holds for the effectiveness factor upon using Equation 18.27 in the asymptotic region:

η=2n+11LDeknCAs(n−1)

Note that η = 1/ϕ for a first-order reaction in the asymptotic region. Now if we wish to write the previous result for an nth-order reaction in a similar format as: η = 1/Λ, the Thiele modulus Λ should be defined as

This is known as the kinetic generalized Thiele modulus. Now we have η = 1/Λ for any kinetics, but only for the asymptotic case.

The expression for η is then generalized as

This expression is strictly valid only in the asymptotic region where tanh(Λ) tends to one but is used for the entire range of Λ values as an approximate solution.

Further, shape normalization can be introduced in order to apply this to other shapes as well. The length parameter is now changed to V_p/S_e and the Thiele modulus is further generalized as

The expression for η given by Equation 18.29 is then used for the nth-order reaction as an approximation for the entire range of Thiele values and for any shape of catalyst. This approximate method of calculation of the effectiveness factor is known as the Bischoff (1965) approximation.

The following reaction scheme is used in the the analysis presented in this section:

A + νB → Products

The diffusion equations for species A and B both have to be solved together here. Both of these concentrations are lower in the pellet compared to the surface. We illustrate the method by taking a slab geometry and a bimolecular (1,1) order reaction. Note that a product concentration increase in the pellet can also be computed by a similar procedure.

The model equations to be solved are as follows for components A and B:

and

The concept of a limiting reactant is very useful here. The reactant whose value of its surface concentration times the diffusivity is lower than the other is usually the limiting reactant. Species A is limiting if

q=DeBCBsνDeACAs>1

and vice versa. The second species is called the excess reactant. For further discussion A can be assumed to be limiting without loss of generality. Thus if B is limiting, the notations can be switched.

One of the important relations that is useful here and also in a general context is the invariant property of the equations. Thus by combining the equations for A and B where we have the common rate term we find the following relation holds between the concentrations of species A and B:

DeBd2CBdx2=νDeAd2CAdx2

The integrated form suggests that

CB=CBs−νDeADeB(CAs−CA)

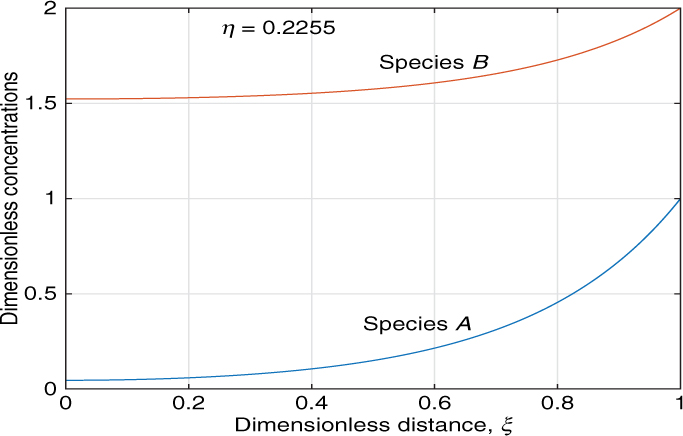
Hence C_B (the excess reactant) can be eliminated in Equation 18.31 and a single differential equation can be solved for A only. The number of differential equations to be solved is thus reduced to one. In the asymptotic region an analytical value can also be obtained by the p-substitution method since we have only one differential equation to handle. An illustrative result is shown in Figure 18.4.

The results shown in this figure are for a slab geometry with ϕ = 3 and q = 2.0. Here species B is the excess reactant since q > 1. Note that the concentration of the excess reactant (B) drops only marginally in the catalyst while that of the limiting reactant drops much more significantly here. The effectiveness factor can be calculated as 0.2255 for this case. Analysis for multiple reactions follows a similar methodology.

• Hydrogenation reactions: Examples include hydrogenation of glucose to sorbitol, unsaturated oils, nitrocompound, aldehydes and esters, and so on.

• Hydrodesulfurization of diesel to remove sulfur compounds.

• Hydrocracking of petroleum fractions using supported metal catalysts to produce lower molecular compounds, such as the gasoline fraction from heavy oil.

• Methanol synthesis from a CO and H₂ gas mixture in the liquid phase with suspended solid catalyst.

• Fisher-Tropsh synthesis from syngas to produce fuels where synthesis gas (CO, H₂ mixture) is converted to heavy hydrocarbon fractions.

• Oxidation reactions; these include oxidation of cumene, phenol, p-xylene, and so on, using oxides of Cr, Cu Co, and so on, as solid catalysts. Note that use of soluble homogeneous catalysts is more common for oxidation and such reactors belong to the category of two-phase reactors.

• Slurry type: Here the catalyst particles are suspended in a liquid with gas being simultaneously sparged into the liquid. The dispersion of the gas and the suspension of the solid catalyst can be done simply by bubbling the gas (bubble column reactor) or by mechanical agitation.

• Fixed bed type: Here the catalyst is stationary and the gas and liquid flow over the catalyst bed similar to a packed bed absorption column. The flow may be cocurrent downward (e.g., trickle bed reactor shown in Figure 1.4) or concurrent upflow (packed bubble column reactor) or countercurrent flow over a packed catalyst bed.

Relative comparisons and the choice of reactors are discussed by Ramachandran and Chaudhari (1983), Mills et al. (1992), and other references; these should be consulted if you are designing these types of reactors. The focus here is mainly on mass transfer effects and how the effectiveness factor concept is useful to calculate the rate of reaction for a simple first-order reaction.

1. Transport of gas from bulk gas to the bulk liquid. This can be modeled using an overall mass transfer coefficient from gas to liquid:

   −RAυ=KLagl(CAg*−CAL)
   CAg* is the saturation solubility of the gas in the liquid based on the bulk gas concentration of gas A. C_AL is the concentration in the bulk liquid. The RAυ is the volumetric absorption of A in the system which equals the rate of reaction of A per unit reactor volume. This step has a resistance of 1/K_La_gl.

2. Transport of dissolved gas from the bulk liquid to the catalyst surface. This can be modeled using a solid–liquid mass transfer coefficient:

   −RAυ=klsals(CAL−CAs)

   Here k_ls is the intrinsic liquid–solid mass transfer coefficient and a_ls is the external surface area of the catalyst per unit reactor volume. This step has a resistance of 1/k_lsa_ls.

3. Internal diffusion with reaction. This can be modeled using k₁ η as the rate coefficient:

   −RAυ=wk1ηCAs

   A simple first-order kinetics is used here. w is the mass of the catalyst per unit reactor volume. This step has a resistance of 1/wk₁ . The rate constant k₁ here is defined on the mass of the catalyst.

   Usually species A will react with a second liquid phase B, which gets transported to the catalyst as well. However if the second species is in excess, the reaction may be approximated as pseudo-first-order case shown here. The details of surface interactions such as adsorption on the active surface followed by reaction are also lumped into the rate constant. The effect of pore diffusion is captured by using the effectiveness parameter, which in turn depends on the Thiele modulus.

Each of the transport steps contribute to a corresponding resistance. For a linear process the resistances can be added. The overall rate can be then calculated as

−RAυ=CAg*[1KLagl+1klsals+1wk1ηc]−1

where η_c in turn can be calculated based on the Thiele parameter for the catalyst.

where k_e is the effective conductivity of the catalyst and ΔH is the heat of reaction. The local rate of disappearance f(C_A, T) is now a function of both the pore concentration and the temperature at any point in the pellet.

The boundary conditions are specified as follows: no flux condition is imposed at the pore end (x = 0) for both heat and mass:

at x =0 dC_A/dx = 0; and dT/dx = 0

At the pore mouth (x = L) the flux into the pellet must match the transport through the gas film. This leads to the following boundary conditions:

For mass transport:

De(dCAdx)x=L=km(CAg−CA,x=L)

For heat transport:

ke(dTdx)x=L=h(Tg−Tx=L)

The dimensionless mass and heat transport equations are then as follows: the mass balance equation is

Here f* is a scaled rate of reaction, defined as

f* = f(C_A, T)/[f(C_Aref , T_ref)]

ϕ² is a Thiele modulus based on reference conditions:

ϕ2=f(Cref,Tref)L2DeCref

The dimensionless heat balance equation is

where β is the dimensionless parameter (thermicity group), defined as

Note that β takes a positive value for exothermic reactions and a negative value for endothermic reactions.

The dimensionless rate has to be appropriately defined, including the temperature effect on the rate constant. For example, using the Arrhenius equation, the dimensionless rate for a first-order reaction can be expressed as

where γ = E/R_gT_ref . E is the activation energy for the reaction. Parameter is a dimensionless group sometimes referred to as the Arrhenius number. The governing equations and the boundary conditions shown in Section 18.5.1 to be solved are then calculated as follows. The species mass balance is:

and the heat balance is

At the center the no flux condition is used for both the concentration and the temperature:

At ξ = 0, dc_A/dξ = 0; d /dξ = 0

The conditions at ξ = 1 can be related to the Biot numbers for heat and mass:

(dcAdξ)s=Bim(cAg−cAs)

(dθdξ)s=Bih(θg−θs)

Here the subscript s is used for ξ = 1, that is, the surface values. The subscript g is used for the bulk values. For the particle problem (local particle-scale model) we can set c_g and θ_g as one since the reference concentration and temperature are the bulk values.

The Biot numbers for mass and heat are defined as

Bi_m = k_mL/D_e

and

Bi_h = hL/k_e

This completes the problem formulation. The problem requires a numerical solution in general.

The results are often shown in terms of an effectiveness factor as a function of Thiele modulus, defined as

η=∫01cAexp[γ(1−1/θ)]dξ

Even for this simple first-order reaction, the overall effectiveness factor is a function of five parameters shown previously. It is a numerical problem with a daunting solution and has been the subject of many research papers. However, certain features can be examined even without solving the full set of equations. Let us now examine if we can calculate the maximum temperature rise (exothermic case).

Hence the integration of this equation twice leads to

This is an invariant of the system.

The maximum value of the temperature occurs for an exothermic reaction when the center concentration drops to zero. This occurs in the strong pore diffusion resistance for mass transfer. Hence an estimate of the internal gradients is

Here θ_c is the center temperature. Further the maximum value of c_As is one. Hence the dimensionless maximum temperature difference between the center and surface is β. Using dimensional values we find the following expression:

The maximum difference occurs when C_Ac is nearly zero; hence this analysis provides a quick method of calculating the maximum internal temperature that can develop in the catalyst.

The temperature rise across the gas film can be related to the measured rate of reaction if an estimate of the film heat transfer coefficient is made. This is simply a heat balance across the gas film, which is observed by rewriting this as

The left-hand side is heat transferred from the solid while the right-hand side is the heat generated due to reaction in the pellet. Note that V_p/S_e is the characteristic length parameter, L_c.

The above relations enable a rapid determination of the relative importance of external and internal temperature gradients. It can be, for instance, used to determine whether the pellet is operating under near isothermal conditions or whether a temperature correction to the data is necessary.

Detailed numerical results for various combination of parameters can be generated, for example, using BVP4C with MATLAB. The solution can show multiple steady states for a certain range of parameters and the effectiveness factors can be larger than one. This happens only for an exothermic reaction where the interior of the catalyst is hotter than the bulk gas. The rate increase due to temperature rise can often compensate for the rate decrease due to concentration increase. This can cause effectiveness factors to be greater than one.

In the next two sections, we discuss two numerical tools to solve diffusion-reaction problems. The first tool is based on orthogonal collocation and is suitable for 1-D problems in the three standard geometries. The second tool is a finite difference method and is suitable for 2-D and 3-D problems.

Collocation points are chosen differently for each of the three geometries so as to minimize the error in the calculation of the average rate of reaction or equivalently the effectiveness factor. Again these details are not addressed here as the main theme is to demonstrate the numerical implementation of the method and to provide useful code. The key result needed from the user point of view is that the Laplacian at each interior collocation point (or node) is approximated as an algebraic equation as shown in Figure 18.6.

This equation, known as the discretization formula, is applied at all interior nodes, that is, i = 1 to nt – 1, generating a set of algebraic equations. The discretization is not applied at the boundary node at ξ = 1. Instead the set of equations is augmented by applying the boundary condition at the node designated as nt. This may be a simple Dirichlet for concentration (c = 1) or a Robin boundary. A Robin boundary needs an approximation of the first derivative, which is given by the A matrix:

Thus nt equations for nt variables are obtained. This set of nonlinear algebraic equations can be solved in an iterative manner by the Newton-Raphson method, which requires the linearization of the rate term f(c) at each level of iteration.

For a sphere the values of the A and B matrices for a two-point collocation are listed in the following. In addition, the quadrature weights w to approximate the integral of the concentration and the location of the points ξ are also given.

Consider the solution of the following problem:

Here x and y are treated as dimensionless variables. c_A is a dimensionless concentration and ϕ is the Thiele modulus.

The domain is divided into meshes along the x- and y-directions with a chosen scale Δx and Δy in each direction. We now abbreviate c_A by c.

In the x-direction the approximation at node i is

(∂2c∂x2)i=ci−1,j−2ci,j+ci+1,jΔx2=O(Δx2)

Similarly in the y-direction we use

(∂2c∂y2)j=ci,j−1−2ci,j+ci,j+1Δy2=O(Δy2)

Hence the finite difference discretization applied at node (i, j) leads to

For direct iteration purposes, the equation is rearranged with c(i, j) as the term on the left-hand side and with all the other terms moved to the right-hand side:

c NEWi,j=[ci−1,j+ci+1,j]Δy2+[ci,j−1+ci,j+1]Δx22(Δx2+Δy2)+ϕ2*Δx2*Δy2

Here the old values (values at previous iteration) are used on the right-hand side and these are known. This permits the calculation of c at node (i, j) (the new value). By sweeping over all the nodes one round of iteration is completed and all the old values are replaced by the new values calculated using the left-hand side of the preceding equation. This sets up an iteration scheme that converges to the solution after a few rounds of updating the concentration values. Illustrative results are shown in Figure 18.7.

The contour plots of the results in Figure 18.7 are for ϕ = 3. The center concentration is found to be equal to 0.5614. The effectiveness factor can be computed either from the average concentration or by calculation of the flux values at the boundary. Both approaches will give (nearly) the same result. The value is 0.7899. A shape-normalized approach gives a value of 0.8469.

The iteration scheme now is

cNEWi,j=[ci−1,j+ci+1,j]Δy2+[ci,j−1+ci,j+1]Δx2−ϕ02*Δx2*Δy22(Δx2+Δy2)

The results are shown in Figure 18.8 for ϕ₀ = 3. If this parameter is increased you will find a region of negative concentration in the center of the system. This indicates the onset of starvation. It can be shown that a Thiele modulus of 3.685 leads to starvation.

The two coefficients κ₀ and κ₁ are obtained by Taylor series approximation at the current value of the nodal concentration, denoted as c*_A here:

and

In the iteration scheme κ₀ is treated as a zero-order reaction term and κ₁ as a first-order term. These terms change values during each iteration as they depend on the current value of the nodal concentration. Hence the iteration scheme is a combination of a first-order and a zero-order reaction.

For, example for a second-order reaction f(cA)=cA2 and we have κ0=−cA*2 and κ1=2cA* where * denotes the old values, that is, the values at the previous iteration. The κ₀ and κ₁ are adjusted at each iteration until the iteration values at all the nodes converge.

Here s is the surface node, s – 1 is the next node adjacent to it, and s – 2 the third node from the surface.

If a no flux condition is applied at the Neumann boundary node, the normal flux is set to zero and concentration values at the surface node are given as

cs=43cs−1−13cs−2

Thus the surface values for these nodes are updated using this equation at each iteration along with the interior values.

Along a Robin boundary the boundary condition is

(dcdn)s=−Bi(cs−cb)

Using Equation 18.52 as the approximation for the normal derivative and rearranging, the following expression is obtained for the surface concentration:

cs=4cs−1−cs−2+2ΔsBicb2ΔsBi+3

where Δs is the mesh spacing at these nodes. Thus along a Robin boundary the iteration is adjusted to maintain this value for c_s.

A model for a plug flow case is considered here for an isothermal system with no appreciable change in gas velocity. The species mass balance equation based on a mesoscopic control volume is

In – out + generation = zero

The generation is calculated as the rate of reaction based on the local gas concentration (and temperature for non-isothermal reactions) times the local effectiveness factor. The effectiveness factor accounts for the effect of concentration drop within the catalyst and in the gas film as well. The rate of reaction is based on the volume of the catalyst. Since the mass balance is based on the total control volume (gas+solid) the rate should be multiplied by the catalyst volume per unit bed volume (1 – ∊_B) with ∊_B being the bed porosity, that is, the volume of the gas per unit volume of the bed. Putting all this together the generation term is

Generation = (1 – ∊_B)R_A(gas)η

R_A(gas) is the rate of reaction based on the local gas concentration at a given point in the reactor. The effectiveness factor thereby couples the reactor-level and particle-level models. The mass balance for the concentration C_A in the gas phase is therefore

uGdCAdz=(1−∊B)RA(gas)η

This can be integrated by a finite difference marching scheme in z or by any solver such as ODE45. The point to note is that is a function of local concentration C_A (unless the reaction is first order at isothermal conditions). Hence at each point of the integration scheme, the value of has to be calculated and incorporated in the marching scheme. For a non-isothermal reaction both mass and heat balance for the gas phase has to be solved together with the effectiveness factor computed from the particle scale model shown in Section 18.5 locally at each axial location. This is a challenging computational problem.

A simple illustration for a power-law kinetics under isothermal conditions is provided in the following. The kinetics is represented as −RA=knCAn. The gas phase balance is

This is written is dimensionless form as

where ζ is z/L, the dimensionless distance. The parameter Da is the Damkohler number, defined as

Da=(1−∊B)knCA,inLuG

The calculation of η can be simplified by using the generalized Thiele modulus. For a nth-order reaction the Thiele modulus is proportional to cA(n−1)/2) as can be garnered from Equation 18.28. Hence the local Thiele modulus can be written in terms of the inlet Thiele modulus Λ_i as

Λ=ΛicA(n−1)/2

The effectiveness factor can be calculated as tanh(Λ)/Λ at each location. Using these in Equation 18.54, the concentration change in the gas phase is given by the following differential equation:

This is now in a form ready for the ODE45 solver. The reactor exit conversion is now dependent on two dimensionless parameters: Damkohler number and the inlet Thiele modulus.

c_A,e = exp[–(1 – ∊_B)k₁ ηL/u_G]

The equation resembles a plug flow reactor and is often represented as

Here k_app is an apparent rate constant:

k_app = (1 – ∊_B)k₁ η

Equation 18.56 can be used to fit the reactor data, but the fitted value of apparent rate constant is not a true rate constant and will in this case vary with particle size if internal gradients are rate limiting. Hence corrections for the internal diffusional effects have to be applied to get the value of the true rate constant.

Table 18.2 Exit Concentration in a Packed Bed Reactor for Power-Law Kinetics

Λi	n = 1	n = 2
0.1	0.0503	0.2503
1.0	0.1017	0.2786
10.0	0.7408	0.7561

The results are for Da = 3 for various values of the inlet Thiele modulus. The effectiveness factor varies along the reactor for a second-order reaction, is lower near the inlet, and increases toward the exit of the reactor for a second-order reaction. This is accounted for in the numerical scheme. For low values of the inlet Thiele modulus, the effectiveness factor is one throughout and an exit concentration is 1/(1 + Da) or 0.25 is observed. The corresponding conversion is 75% At high values of the Thiele modulus, internal diffusion limits the rate and the conversion is only 25% at the same gas residence time.

18.2 How is the Thiele modulus defined and what is its significance?

18.3 If the concentration profile is known, state two ways of calculating the average rate of reaction for the catalyst.

18.4 Define the Thiele modulus for zero- and second-order reactions and verify dimensional consistency.

18.5 What is the Biot number and what role does it play in affecting the reaction rate in a porous catalyst?

18.6 Under what conditions does the rate of reaction become dependent on the catalyst size? Does it increase or decrease with size?

18.7 If the rate of reaction decreases linearly with catalyst size, what is the controlling resistance?

18.8 If the rate of reaction does not change with catalyst size, what is the controlling resistance?

18.9 What is the definition of the shape-normalized Thiele modulus? Why is it useful?

18.10 Can a zero-order reaction exhibit a dependency on the bulk gas concentration? If so, when?

18.11 Define the generalized Thiele modulus for an nth-order reaction.

18.12 A second-order reaction is taking place under strong pore diffusional resistance, that is, ϕ > 3. If the pressure is doubled by what factor would the rate change?

18.13 What dimensionless parameter is indicative of the maximum temperature difference between the center and the surface of a catalyst?

18.14 Can the effectiveness factor be larger than one? When?

18.15 A second-order reaction is taking place in a packed bed reactor. How would the effectiveness factor change along the axial length in the reactor?

18.16 A half-order reaction is taking place in a packed bed reactor. How would the effectiveness factor change along the axial length in the reactor?

ϕ*=ϕs+1

Show that the results for the three geometries are quite close when is plotted as a function of ϕ*, which is referred to as the generalized Thiele modulus.

18.2 Robin boundary condition. Consider the same problem as above but now use a Robin condition at the surface. Derive an expression for the effectiveness factor as a function of Bi in addition to the ϕ parameter. Do the analysis for all three geometries.

18.3 Choosing an operating catalyst size. The rate of reaction was measured in a powdered catalyst of fine size and was found to be 200 mol/m³s. Assume the reaction to be first order and there are no internal gradients. The gas is at 1 atm and 400 K with a mole fraction of 0.1 for the reactant. Now we wish to change to a spherical pellet catalyst and we have an estimate of the effective diffusivity of the catalyst. D_e = 2 × 10^–6 m²/s. From pressure drop considerations we wish to operate at a Thiele modulus of 0.4 or so. What should be the radius of the catalyst? How much will the catalyst effectiveness factor drop?

18.4 First-order catalytic reaction: effect of particle size. A first-order catalytic reaction was carried out with two different-sized spherical pellets and the following data was reported. For run 1: particle radius = 10 mm; observed rate = 3 × 10^–5 mol reacted per cm³ catalyst per sec. For run 2: particle size = 1 mm; observed rate = 15 × 10^–5 mol reacted per cm³ catalyst per sec. Estimate the Thiele modulus and the effectiveness factor for each of the above runs. Estimate the rate constant and the effective diffusion coefficient for this system. Use a bulk gas phase concentration of A as 100 mol/m³. Neglect gas side resistance.

Hint: Note that from the definitions the following relations can be deduced:

Rate 1Rate 2=η1η2

and

ϕ1ϕ2=R1R2

With these relations and the equation relating to ϕ you will be able to derive an equation for ϕ₁ (or ϕ₂); solve this and get the required results.

18.5 First-order catalytic reaction: strong pore resistance case. A first-order catalytic reaction was carried out with two different-sized spherical pellets and the following data was reported. For run 1: particle radius = 10 mm; observed rate = 3 × 10^–5 mol reacted per cm³ catalyst per sec. For run 2: particle size = 5 mm; observed rate = 6 × 10^–5 mol reacted per cm³ catalyst per sec. Explain why it is not possible to estimate both the rate constant and pore diffusivity from this data. What can be estimated? Assume the bulk concentration is known.

18.6 Shape normalization. A first-order reaction has a rate constant of 5 sec^–1 and is taking place in a catalyst with an effective diffusion coefficient of 10^–6 m²/s. Use shape normalization to estimate the approximate value of the effectiveness factor for the following cases: (1) Long cylinder with a radius of 4 mm; (2) a short cylinder with a radius of 4 mm and a length of 4 mm; (3) a long annular cylinder with an outer radius of 4 mm and an inner radius of 2 mm; (4) a short annular cylinder with an outer radius of 4 mm, an inner radius of 2 mm, and a length of 4 mm. For case (1), compare the value with the exact answer.

18.7 Weisz modulus. For diagnostic purposes a dimensionless quantity called the Weisz modulus is useful. This is a combination of the Thiele modulus and the effectiveness factor and is defined as

Φ_W = ϕ²η

Show that the Weisz modulus is related to the measured rate of reaction as

ΦW=Lc2−〈RA〉DeACAb

Hence conclude that it can be directly calculated from the measured rate. A measured value or estimated value of the internal diffusion in the pore is needed for this. Show that ifΦ_W < 0.4 or so the internal gradients are negligible and the measured rate is representative of the true kinetic rate constant. Replot the η versus ϕ plot as a η versus Φ_W plot. What is the usefulness of this new plot?

18.8 Zero-order reaction in a sphere. Many hydrogenation reactions over Pd-supported porous catalyst show a zero-order kinetics. Consider such a reaction in a spherical catalyst. Show that the concentration at the center of the catalyst drops to zero if the Thiele parameter, defined as k0R2/(DeCAs), is equal to 6. Here C_As is the concentration of the reactant (hydrogen) at the surface of the catalyst. Based on this conclude that the pore diffusional resistances are unimportant and the effectiveness factor is equal to one if the surface concentration is maintained above k₀R²/6D_e.

18.9 Second-order reaction: sulfur removal from diesel. Sulfur compounds present petroleum fractions such as diesel that can be removed by contact with a porous catalyst containing active metals such as Mo in the presence of hydrogen. If the catalyst size is a sphere of radius 3 mm and the concentration of sulfur in the liquid surrounding the catalyst is 2 mol/m³ find the rate of reaction. Assume the reaction is second order in sulfur concentration with a volumetric rate constant of 0.5 m³/mol.s. The effective diffusion coefficient of sulfur compounds in the liquid-filled pores is estimated as 6 × 10^–10 m²/s. Use a slab geometry as an approximation and find the characteristic length parameter L. Define and calculate the generalized Thiele modulus for this second-order reaction. Calculate the effectiveness factor based on the generalized Thiele modulus.

18.10 Fractional order: dead zones. Similar to the zero-order reaction, the fractional order reactions exhibit the existence of dead zones beyond a critical value of the Thiele modulus. The problem examines the derivation of this value.

Start with the dimensionless version of Equation 18.18 and use the p-substitution to eliminate ξ. Use the condition that if c_A = 0 then p = 0 (i.e., a dead zone exists near the center) and derive an expression to get the following expression for the concentration gradient:

dcAdξ=ϕ2n+1cA(n+1)/2

At the critical Thiele modulus ϕ_c, c_A is just equal to zero at ξ = 0. Use this as the boundary condition, integrate the above equation by separation of variables and then show that the value of this modulus is

ϕc=2(n+1)1−n

18.11 Porous catalyst with series reactions. Consider a porous catalyst with a series reaction represented as

A → B → C

Write governing equations for A and B. Express these in dimensionless form. Solve the equations for a case where the dimensionless concentration at the catalyst surface is one and zero for A and B respectively. Note: Both concentrations are normalized with the concentration of A at the surface. Calculate the dimensionless gradient for these two species at the surface. From these expressions calculate the selectivity parameter, defined as

S = –(dc_B/dξ)/(dc_Adξ) at ξ = 1

State the significance of this parameter. Plot S as a function of ϕ and show how the high selectivity changes with the Thiele modulus.

18.12 Bimolecular reaction: asymptotic solution. Derive an expression for the surface flux modulus for a bimolecular second-order reaction using the p-substitution approach. Show that the generalized Thiele modulus should be defined as follows:

Λ=ϕ*1−1/3q)

Here ϕ* is the shape-normalized Thiele modulus, assuming the reaction to be pseudo-first order in species B, and q is the effective concentration ratio of B to A in the bulk gas.

18.13 Bimolecular reaction in a porous catalyst. Selective catalytic reduction of NO_x with NH₃ is studied in a porous catalyst of 4 mm diameter. The internal diffusivity was estimated independently as D_A = 0.03 × 10^–4 m²/s and D_A = 0.05 × 10^–4 m²/s. The reaction is second order with a rate constant of 2 m³/mol sec. The temperature was 600 K and the total pressure was 1 atm; the partial pressures of NO and NH₃ were 500 kPa and 1000 kPa, respectively. Which reactant is limiting? Simulate the profiles in the interior of the catalyst. Find the effectiveness factor. To what extent is the diffusion limiting?

18.14 Hydrogenation of butynediol. Hydrogenation of butynediol was carried out in a slurry reactor with a Pd-based catalyst of size 0.01 cm with a catalyst loading of 0.2 kg/m³. The density of the catalyst is 1500 kg/m³. The reaction is bimolecular (first order with respect to both A and B) with a rate constant of 0.048 m⁶/kg kmol s based on the mass of the catalyst. The mass transfer parameters are as follows: k_La_gl = 0.3 s^–1 and k_ls = 0.005 cm/sec for hydrogen and 0.009 m/s for butynediol. The diffusion coefficient is 0^–9 m²/s for hydrogen. The Henry constant for hydrogen is 0.01 mol/m³ atm. The initial concentration of butynediol is 2.5 M. Find the time needed for 95% conversion of butynediol.

18.15 Internal and external temperature gradients. Catalytic cracking of gas oil is done at 903 K and 1 atm with a silica-alumina catalyst of 1.62 mm diameter. The effective diffusivity of the catalyst is 8 × 10^–8 m²/s and the effective thermal conductivity of the catalyst is 0.36 W/m.K. The heat of the reaction is –167 kJ/mol and the activation energy is 176 kJ/mol. The mass transfer coefficient is 1 m/s and the heat transfer coefficient is 400 W/m²K. The measured rate is 0.4 mol/m³s. Estimate the internal and external temperature differences.

18.16 Second-order reaction in a packed bed. A second-order reaction is taking place in a packed column with 3 mm radius particles. The internal diffusivity is 10^–2 cm²/s. The porosity of the bed is 0.4 and the rate constant is 0.75 m³/mol.s. The concentration of A in the feed is 12 mol/m³ and the volumetric flow rate is 0.5 m³/s. Find the reactor volume needed to get 90% conversion. What are the values of the effectiveness factor at the inlet and the exit of the reactor?

18.17 Two-point collocation for three geometries. The matrices needed for a slab and cylinder are shown in the following. The values for a sphere were shown earlier.

For slab geometry the values are as follows:

---

A =  [  –1.1180   1.1180
        –2.5000   2.5000]
B = [   –2.5000   2.5000
        –2.5000   2.5000]
x =    0.4472   1.0000
w =     0.8333    0.1667

---

The values for the cylindrical geometry are as follows:

---

A = [   –1.7321 1.7321
   –3.0000 3.0000]
B = [    –6    6
   –6    6]
w =    0.3750    0.1250
x =     0.5774    1.0000

---

Use these to find the effectiveness factor for a second-order reaction with ϕ = 2 for all three geometries. Compare the results with the Bischoff approximation.

18.18 Collocation method for a reaction with substrate inhibition. A reaction with substrate inhibition can exhibit multiple steady states. As an example consider a diffusion-reaction model in a slab geometry with the following form: ϕ2cA/(1+αcA+βcA2). Evaluate the effect of the Thiele modulus, keeping = 110 and = 1000. Compare simulation with two point and five point collocation method. Plot versus ϕ. Show that multiple steady states are likely for a Thiele modulus in the range of 23 to 26.8.

18.19 Collocation method with larger number of nodes. In Example 18.4 we showed the collocation method using only one interior point. This was found to be accurate for moderate values of the Thiele modulus, showing the power of the method. Here we wish to examine the solution for a larger number of points. The collocation matrices for nt = 5 for a slab geometry are presented in Table 18.3. Set up and solve the equations for various values of ϕ for a first-order reaction. Calculate as a function of ϕ with an analytical solution. Repeat for a second-order reaction. Compare the effectiveness factor to that calculated using the shape-normalized Thiele modulus. Verify that the five-point collocation is accurate for most practical applications, unless the Thiele modulus is extremely large. In latter case the asymptotic solution is good enough.

Table 18.3 Collocation Matrices for Five-Point Total Collocation for Slab Geometry.

A = -5.0717    8.6586   -6.3671     4.6458   -1.8656
    -1.4346   -2.6538    6.3920    -3.7114    1.4077
     0.5230   -3.1687   -1.9121     6.6239   -2.0661
    -0.3861    1.8615   -6.7019    -1.6060    6.8325
     0.7615   -3.4682   10.2684   -33.5618   26.0000
B =   -34.4654   44.1493  -14.2677     7.0025   -2.4186
       13.9798  -52.3162   48.8370   -15.1776    4.6771
      -3.1083   33.6001  -94.5282    80.8944  -16.8579
       1.8377  -12.5790   97.4469  -286.6901  199.9845
      38.5462 -170.3650  457.9635  -794.1446  468.0000
w =        0.0251    0.0792    0.1152    0.0956     0.0182
x =     0.2958    0.5652    0.7845    0.9340     1.0000

---