Chapter 14. Mesoscopic Models and the Concept of Dispersion

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Chapter 14. Mesoscopic Models and the Concept of Dispersion

Learning Objectives

After completing this chapter, you will be able to:

Understand how mesoscopic models result from a cross-sectional averaging of differential models.
Identify additional parameters that result upon averaging.
Explain the meaning of the dispersion coefficient.
Model and solve reactor models using the dispersion concept.
Understand the usefulness of the transient response data to determine the dispersion coefficient.
Understand the classical work of the Taylor model for axial dispersion in laminar flows.
Model and solve cocurrent and countercurrent mass exchangers using the dispersion coefficient for each of the phases.

Mesoscopic models use one spatial coordinate oriented in the main flow direction as the primary distance variable. Any concentration variation in the cross-flow directions are represented by average values. We have seen some examples of such models in Chapter 4 and this chapter provides additional details.

A differential model averaged over a cross-section gives us the meso-model. It is useful to understand the process of averaging and how meso-models arise naturally. This also helps us to identify the missing information, the so-called closures, which are needed when using the meso-models. This is the first topic addressed in this chapter.

The main closure relation required is a relation between the cup-mixing average and the cross-sectional average. Commonly this is done using a parameter called the dispersion coefficient. This was introduced in Chapter 4 and simple applications to a homogeneous reactor were demonstrated. Here we present additional information and generally useful MATLAB code to execute the performance calculations. We also show how tracer data can be interpreted to evaluate the dispersion coefficient experimentally.

The concept of dispersion followed from the classic work of Taylor (1953), who developed a theoretical model for this coefficient for some well-defined flow fields. It is useful to understand the details leading to this development; this is presented in this chapter as well.

The mesocopic modeling approach from Chapter 4 for mass exchangers (two-phase systems) is then reviewed and a model for plug-backmixed flow is presented. Further, the plug-plug model shown in Section 4.3.2 is extended to include dispersion. Such models are useful in modeling many separation processes. Both the mass transfer coefficient and the dispersion coefficient for each of the phases are needed as input parameters for such models. Illustrative results are presented for the effect of dispersion on the concentration profiles in mass exchangers.

14.1 Plug Flow Idealization

Meso-models are simple in form and structure and can be formulated in two ways: by the direct use of the conservation for meso control volume, and by averaging of the differential models. In both cases, the convection term depends on the cup-mixed average value while the reaction term depends on the cross-sectional average. The resulting model equation (Equation 4.12) for a first-order reaction (for a constant density system) is revisited here for ease of reading:

\begin{matrix} - 〈 υ 〉 \frac{d C_{Ab}}{dz} = k_{1} 〈 C_{A} 〉 & (14.1) \end{matrix}

$\begin{matrix} - 〈 υ 〉 \frac{d C_{Ab}}{dz} = k_{1} 〈 C_{A} 〉 & (14.1) \end{matrix}$

The left-hand side represents the convection term; the cup-mixing average is the proper concentration to use in defining this term. The right-hand side is the rate of generation term and the cross-sectional average should be used as the measure of concentration here. Thus two types of averages are involved in the same model and there is already a closure problem. Section 4.2 explained this in some detail and should be reviewed at this point before proceeding further. In this chapter we further elaborate on these concepts and in particular discuss the dispersion models in more detail. The plug flow assumption is reviewed first. It is useful to review Section 4.2.1 at this point.

The concept of plug flow is an idealized representation of the cross-direction concentration profile in the reactor. The assumption is that there is no concentration gradient in this direction. that is, the concentration is constant across any cross-section. The velocity profile has to be uniform for this to occur. In addition there should be no other mechanism that can cause a concentration gradient. For example, if a heterogeneous reaction occurs at the wall, then the concentration at the wall will be smaller (or even near zero for a rapid reaction) causing a deviation from plug flow. Similarly if a temperature profile exists then the change in rate due to this causes the concentration to be different at different radial positions, causing the assumption to be invalid.

The plug flow approximation then uses the idealization that C_Ab = 〈C_A〉. For power law kinetics at constant velocity the plug flow model is

- 〈 υ 〉 \frac{d 〈 C_{A} 〉}{dz} = k_{n} {〈 C_{A} 〉}^{n}

$- 〈 υ 〉 \frac{d 〈 C_{A} 〉}{dz} = k_{n} {〈 C_{A} 〉}^{n}$

The performance equations for a simple single reaction with no volumetric change (constant density case) are shown in Table 14.1 for common power law kinetics and are useful for a first level of calculations for many applications. Results are presented for the dimensionless exit concentration, 〈c_A,e〉, in terms of the Damkohler number, which is the key dimensionless groups for such problems. This is defined as

\begin{matrix} Da = k_{n} C_{A, i}^{n - 1} \frac{L}{〈 υ 〉} & (14.2) \end{matrix}

$\begin{matrix} Da = k_{n} C_{A, i}^{n - 1} \frac{L}{〈 υ 〉} & (14.2) \end{matrix}$

Table 14.1 Plug Flow Exit Concentration for Power Law Kinetics

First-order reaction:
	〈c_A,e〉 = exp(–Da)
Second-order reaction:
	$〈 c_{A, e} 〉 = \frac{1}{1 + Da}$ $〈 c_{A, e} 〉 = \frac{1}{1 + Da}$
Zero-order reaction:
	$〈 c_{A, e} 〉 = {\begin{matrix} 1 - D a & if D a \leq 1 \\ 0 & if D a > 1 \end{matrix}$ $〈 c_{A, e} 〉 = {\begin{matrix} 1 - D a & if D a \leq 1 \\ 0 & if D a > 1 \end{matrix}$
Half-order reaction:
	$〈 c_{A, e} 〉 = {\begin{matrix} {\begin{matrix} (\begin{matrix} 1 - D a \end{matrix} / 2) \end{matrix}}^{2} & if D a \leq 2 \\ 0 & if D a > 2 \end{matrix}$ $〈 c_{A, e} 〉 = {\begin{matrix} {\begin{matrix} (\begin{matrix} 1 - D a \end{matrix} / 2) \end{matrix}}^{2} & if D a \leq 2 \\ 0 & if D a > 2 \end{matrix}$

Note that this represents the ratio of the mean residence time in the reactor to the reaction time. Also note this is a function of the inlet concentration, C_A,i, unless the reaction is first order.

Note that the results in Table 14.1 are similar to the batch reactor with the mean passage time, defined as L/ 〈v〉, replacing the batch time. The equations are applicable for a constant density system, that is, 〈v〉 is treated as a constant.

Extension to systems where the average velocity is changing in the flow direction due to changes in density of the system can be readily accomplished as well. Additional relations for change in average velocity can be computed based on an overall mass balance and included in the model.

The dispersion model introduced in Section 4.2.2 and continued in the following section is an attempt to correct for the deviation from plug flow. More details are presented next.

14.2 Dispersion Model

Plug flow assumes no mixing in the flow direction. We can account for the deviation by assuming there is a mixing component superimposed on the convective flow; this is as though some diffusion is taking place in the flow direction. A dispersion parameter is then imposed and the in and out terms are modified. Equation 4.15 shows how the additional terms get added to the plug flow model and it may be useful to review that at this stage. The following second-order differential equation for the cross-sectional average concentration applies:

\begin{matrix} D_{E} \frac{d^{2} 〈 C_{A} 〉}{d z^{2}} - 〈 υ 〉 \frac{d 〈 C_{A} 〉}{dz} + 〈 R_{A} 〉 = 0 & (14.3) \end{matrix}

$\begin{matrix} D_{E} \frac{d^{2} 〈 C_{A} 〉}{d z^{2}} - 〈 υ 〉 \frac{d 〈 C_{A} 〉}{dz} + 〈 R_{A} 〉 = 0 & (14.3) \end{matrix}$

This can be obtained by a differential mass balance or the use of the relation in 1.28 in Chapter 1 to close the cup mixing average terms on the left-hand side of Equation 14.1. Here 〈R_A〉 is based on the cross-sectional averaged rate of reaction. For example, for a first-order reaction, 〈R_A〉 = –k₁ 〈C_A〉. Now all terms are in terms of the cross-sectional average and the model is closed. This dimensionless form of the model and the dimensionless parameters needed to calculate the reactor performance is presented next.

Dimensionless Parameters

The distance is scaled by the reactor length and a dimensionless distance η = z/L is used. The concentration is scaled by the inlet concentration. The notation 〈c〉 is used for the dimensionless concentration of A; that is, the subscript A is dropped for brevity.

The resulting equation for a first-order reaction is

\begin{matrix} D_{E}^{*} \frac{d^{2} 〈 c 〉}{d η^{2}} - \frac{d 〈 c 〉}{dη} - Da < c > = 0 & (14.4) \end{matrix}

$\begin{matrix} D_{E}^{*} \frac{d^{2} 〈 c 〉}{d η^{2}} - \frac{d 〈 c 〉}{dη} - Da < c > = 0 & (14.4) \end{matrix}$

The three terms can be identified as disperion, convection, and reaction. The dimensionless parameter appearing on the first term is referred to as the dispersion number. This is defined as

\begin{matrix} D_{E}^{*} = \frac{D_{E}}{〈 υ 〉 L} & (14.5) \end{matrix}

$\begin{matrix} D_{E}^{*} = \frac{D_{E}}{〈 υ 〉 L} & (14.5) \end{matrix}$

The second parameter appearing in the reaction term is the Damkohler number, Da, which equals k₁L/ 〈v〉 for first-order reaction and is defined by Equation 14.2 for a power-law kinetics.

Thus two dimensionless parameters are needed in the disperion model; plug flow needs only one. Also note that the plug flow model is recovered if D*_E approaches zero. It can also be shown that the backmix model is recovered if D*_E approaches infinity.

The reciprocal of D*_E is defined as the dispersion Peclet number:

P e * = \frac{1}{D_{E}^{*}} = \frac{〈 υ 〉 L}{D_{E}}

$P e * = \frac{1}{D_{E}^{*}} = \frac{〈 υ 〉 L}{D_{E}}$

Note: This should not be confused with the Peclet number, Pe, introduced in 9.3.1. Both definitions have a similar grouping format but in one case (Pe*) we use the axial dispersion coefficient while in the other case (Pe) we use the molecular diffusion coefficient. In some books Pe* is referred to as the Bodenstein number. In terms of the (dispersion) Peclet number the model is written as

\begin{matrix} \frac{1}{P e *} \frac{d^{2} 〈 c 〉}{d η^{2}} - \frac{d 〈 c 〉}{dη} - Da 〈 c 〉 = 0 & (14.6) \end{matrix}

$\begin{matrix} \frac{1}{P e *} \frac{d^{2} 〈 c 〉}{d η^{2}} - \frac{d 〈 c 〉}{dη} - Da 〈 c 〉 = 0 & (14.6) \end{matrix}$

Hence two parameters are needed to describe the reactor behavior, unlike the plug flow model where Da alone is sufficient. Note that the plug flow model is recovered if Pe* is large.

The application of the dispersion model requires the following considerations:

How do we know what the value of D_E is? Can we predict it from theory? Can we measure it for a real reactor?
What boundary conditions should be used in the solution of the dispersion model? Note that two boundary conditions are now needed.
How do we solve this for multiple reaction case and complex nonlinear kinetics?

The answers to these questions will be addressed as we progress through this chapter. First we start with the boundary conditions and the solution to the dispersion model.

14.2.1 Boundary Conditions

The boundary conditions to be used have been the subject of considerable discussion and many research papers. See Froment et al. (2011) for key references. The boundary conditions depend on what assumptions are used in the inlet and outlet. At both of these points, the reactor is characterized as “closed” or “open.” A closed inlet boundary is considered one where plug flow exists prior to the inlet section. A open boundary is one where the flow has the same characteristics within and adjacent to the test section, that is, there is dispersion across the plane under consideration. Similar definitions are used for the exit boundary. Thus there can be four different combinations for the boundary conditions. Most commonly closed-closed or open-open conditions at the inlet and exit respectively are used.

The Danckwerts boundary conditions are commonly used in the context of the dispersion model, assuming a closed-closed system. A material balance at the inlet leads to

\begin{matrix} \begin{matrix} At η = 0, & \frac{1}{P e *} \frac{d 〈 c 〉}{d η} = 1 \end{matrix} & (14.7) \end{matrix}

$\begin{matrix} \begin{matrix} At η = 0, & \frac{1}{P e *} \frac{d 〈 c 〉}{d η} = 1 \end{matrix} & (14.7) \end{matrix}$

This condition assumes some drop in concentration due to dispersion as we enter the reactor, that is, at η = 0⁺, where the concentration is not the same as the concentration at η = 0^–, that is, just before the entry.

The schematic of the assumptions in the closed-closed approximation is shown in Figure 14.1. The figure also illustrates the balance across the inlet plane, η = 0, which leads to the above boundary condition. The concentration is discontinuous when crossing this plane.

Diagrammatic representation shows the conditions used for closed-closed boundary conditions.

Two horizontal lines divided into three parts by two vertical lines resembles the setup of closed-closed boundary conditions. The first vertical line is at z equals 0 and the second vertical line is at z equals L. From left to right: the first segment is Inlet section, with No dispersion D subscript E equals 0. The second segment is Reactor, with Finite dispersion, D subscript E is not equal to 0.0, the third segment is Outlet section, with No dispersion, D subscript E equals 0.0. A vertical dotted line is drawn below the first vertical line at z equals 0. To the left of the dotted line is the expression "In equals v times C subscript A (0 superscript minus)." To the right of the dotted line is the expression "Out equals v times C subscript A (0 superscript plus) minus D subscript E times derivative of C subscript A with respect to z (0 superscript plus). At z equals L, C subscript A continuous, D subscript E times derivative of C subscript A with respect to z equals 0.

Figure 14.1 Schematic of conditions used for closed-closed boundary conditions.

At the exit the stream is allowed to blend smoothly with the outlet fluid, that is, the concentration is assumed to be a continuous function. This leads to

\begin{matrix} \begin{matrix} At η = 1, & \frac{d 〈 c 〉}{d η} = 0 \end{matrix} & (14.8) \end{matrix}

$\begin{matrix} \begin{matrix} At η = 1, & \frac{d 〈 c 〉}{d η} = 0 \end{matrix} & (14.8) \end{matrix}$

14.2.2 Solution for a First-Order Reaction

The solution can be obtained analytically for a first-order reaction and numerically for other cases. The result for a first-order reaction using the boundary conditions stated in the previous section is as follows for the dimensionless exit concentration:

\begin{matrix} 〈 c_{A, e} 〉 = \frac{4 α exp (P e * / 2)}{{(1 + α)}^{2} exp (α P e * / 2) - {(1 - α)}^{2} exp (- α P e * / 2)} & (14.9) \end{matrix}

$\begin{matrix} 〈 c_{A, e} 〉 = \frac{4 α exp (P e * / 2)}{{(1 + α)}^{2} exp (α P e * / 2) - {(1 - α)}^{2} exp (- α P e * / 2)} & (14.9) \end{matrix}$

where

α = \sqrt{(1 + 4 Da / P e *)}

$α = \sqrt{(1 + 4 Da / P e *)}$

The effect of dispersion was shown qualitatively in Chapter 4 and Figure 4.3 should be reviewed again at this stage. The results were for a first-order reaction with Da = 3 and the effect of D*_E (the reciprocal of Pe*) was shown. It was also shown that the results of the two ideal cases, backmix and plug flow, are recovered as 1/(1 + Da) and exp(–Da), respectively. Thus we observe that the reactor behavior is bracketed between these limits.

14.2.3 Nonlinear Reactions

For nonlinear reactions one can use cross-sectional averaging as explained earlier. However, one obtains the cross-sectional average reaction rate as a term. The cross-section average of the rate of reaction is not the same as r(〈c〉), the rate based on the average concentration, unless the reaction is first order. For example, the average of c² is not the same as the square of the average of c. Note that these two averages are the same only if the variance of the radial concentration profile is zero. The unknown variance introduces yet another uncertainty in the dispersion model. One has to assume that

〈r(c)〉 ≈ r(〈c〉)

in order to close the model as a first approximation. This assumption is similar to the micromixed model, now at each local axial location level. With this assumption the dispersion model for power-law kinetics is

\begin{matrix} \frac{1}{P e *} \frac{d^{2} 〈 c 〉}{d η^{2}} - \frac{d 〈 c 〉}{dη} - Da {〈 c 〉}^{n} = 0 & (14.10) \end{matrix}

$\begin{matrix} \frac{1}{P e *} \frac{d^{2} 〈 c 〉}{d η^{2}} - \frac{d 〈 c 〉}{dη} - Da {〈 c 〉}^{n} = 0 & (14.10) \end{matrix}$

The Danckwerts boundary conditions are commonly used. The equation is solved numerically and a CHEBFUN-based solution appears to do the trick. We therefore provide sample code that is written for a series reaction, but it can be used generally.

14.2.4 Dispersion Model: Numerical Code Using CHEBFUN

The problem considered is the simultaneous solution of the following equations:

D_{E}^{*} \frac{d^{2} u}{d η^{2}} - \frac{du}{dη} - Da 1 u = 0

$D_{E}^{*} \frac{d^{2} u}{d η^{2}} - \frac{du}{dη} - Da 1 u = 0$

D_{E}^{*} \frac{d^{2} υ}{d η^{2}} - \frac{d υ}{dη} + Da 1 u - D a 2 υ = 0

$D_{E}^{*} \frac{d^{2} υ}{d η^{2}} - \frac{d υ}{dη} + Da 1 u - D a 2 υ = 0$

which represents consecutive reactions in a tubular reactor with axial dispersion. Equations are in dimensionless form.

Here u is the concentration (cross-section average) of species A, which reacts to form B with a Damkohler number of Da1. Species B, denoted as v, undergoes an additional reaction to form C. The Damkohler number for this is Da2. Both reactions are taken as first order. Due to stoichiometric constraints only A and B need to be tracked and the concentration of the final product C can be found by material balance. The reactor is modeled with a dispersion number D*_E. Danckwerts conditions are used here for both components.

Listing 14.1 Numerical Solution of Dispersion Model

Click here to view code image

% Parameter values used are:
da1= 0.5; DE_star = 0.25; da2 = 1.0; Pe1 = 1/DE_Star;
   Pe2= 1/DE_Star;
% Inlet concentrations are
cin1= 1.; cin2= 0.;
% Set up a CHEBFUN operator
x = chebfun ('x', [0,1]); % distance
u = chebfun ('u', [0,1]); % species A
v= chebfun ('v', [ 0,1 ]) % species B
N = chebop (0,1);
% Define diffusion–convection–reaction operator
N.op = @(x,u,v)[DE_star* diff(u,2)–diff(u,1)–da1*u,...
      DE_Star* diff(v,2)–diff(v,1)+ da1*u–da2*v ]
% Danckwerts boundary conditions at exit
N.rbc = @(u,v)[ diff(u,1), diff(v,1) ];
% Inlet boundary condition; some dispersion allowed
N.lbc = @(u,v)[ diff(u,1)–Pe1.*u+Pe1*cin1 ,...
      diff(v,1)–Pe2*v+Pe2*cin2]
C= N % solution found by overloaded operator
   C = chebfun(C)
plot(C) % plot of solution.

14.2.5 Criteria for Negligible Dispersion

It is useful to know when dispersion effects can be neglected and the plug flow approximation is adequate. The following guidelines are useful:

For slow reactions, dispersion effects are not important. If the exit conversion is less than 30% or so, the mixing pattern in the reactor is not important. The plug model, the backmixed model, and the dispersion model provide nearly the same conversion.
For turbulent flow, dispersion effects are not so significant, unless the reaction is fast. The velocity profiles are nearly flat except in the wall region. Hence the tube behaves almost like a plug. Dispersion effects may need to be considered if the conversion is above 90% or more. The plug flow assumption will provide an underdesign for reactor volume while the backmixed model will provide an overdesign for the same level of conversion.
In long reactors plug flow will be generally achieved. This is because the dispersion number depends on the length of the reactor and becomes small for long reactors; hence the model predictions become close to that for plug flow.

One method to evaluate the dispersion parameter is the tracer method, which we will discuss now.

14.3 Dispersion Coefficient: Tracer Response Method

In this section we discuss the tracer response to a system modeled by a dispersion model. This is an useful technique to experimentally determine the value of the dispersion coefficient in the system. The methodology was introduced in Chapter 13 for the tanks in series model and is similar for the dispersion model. All of the following methods can be used to fit the tracer response curve and the value of the dispersion coefficient can be evaluated: Laplace domain fitting, moment analysis, and time domain fitting.

The calculation of the response in the Laplace domain is presented next. From the Laplace domain solution the moments can be extracted and the variance, which is the necessary equation for the moment method, is calculated. The solution in the time domain is needed for time domain fitting and involves some additional mathematical manipulations. Only the final solution is shown for this case.

The starting point is the dispersion model with the time dependency included but no reaction. In terms of the dispersion Peclet number the model to be solved is

\begin{matrix} \frac{\partial 〈 c 〉}{\partial t *} = \frac{1}{P e *} \frac{\partial^{2} 〈 c 〉}{\partial η^{2}} - \frac{\partial 〈 c 〉}{\partial η} & (14.11) \end{matrix}

$\begin{matrix} \frac{\partial 〈 c 〉}{\partial t *} = \frac{1}{P e *} \frac{\partial^{2} 〈 c 〉}{\partial η^{2}} - \frac{\partial 〈 c 〉}{\partial η} & (14.11) \end{matrix}$

Time is dimensionalized as t* = t/[L/ 〈v〉], that is, scaled by the mean residence time.

Danckwerts boundary conditions are commonly used in the context of the dispersion model. At the inlet we allow some drop in concentration due to dispersion:

\begin{matrix} \begin{matrix} At η = 0, & 〈 c 〉 - \frac{1}{P e *} \frac{\partial 〈 c 〉}{\partial η} \end{matrix} = {〈 c 〉}_{in} (t *) & (14.12) \end{matrix}

$\begin{matrix} \begin{matrix} At η = 0, & 〈 c 〉 - \frac{1}{P e *} \frac{\partial 〈 c 〉}{\partial η} \end{matrix} = {〈 c 〉}_{in} (t *) & (14.12) \end{matrix}$

where 〈c〉_in (t) is the inlet concentration of the tracer. This will depend on the mode of tracer injection. Commonly the step and pulse functions are analyzed.

At the exit, the stream is allowed to blend smoothly with the outlet fluid:

\begin{matrix} \begin{matrix} At η = 1, & \frac{\partial 〈 c 〉}{\partial η} \end{matrix} = 0 & (14.13) \end{matrix}

$\begin{matrix} \begin{matrix} At η = 1, & \frac{\partial 〈 c 〉}{\partial η} \end{matrix} = 0 & (14.13) \end{matrix}$

14.3.1 Laplace Domain Solution

The Laplace transform of Equation 14.11 is

\begin{matrix} \frac{1}{P e *} \frac{d^{2} \bar{c}}{d η^{2}} - \frac{d \bar{c}}{dη} - s \bar{c} = 0 & (14.14) \end{matrix}

$\begin{matrix} \frac{1}{P e *} \frac{d^{2} \bar{c}}{d η^{2}} - \frac{d \bar{c}}{dη} - s \bar{c} = 0 & (14.14) \end{matrix}$

Here $\bar{c}$ $\bar{c}$ is used as the Laplace transform of 〈c〉. The initial tracer concentration in the reactor is normalized to zero.

The equation has the same form as that for the steady state case with reaction with Da now being replaced by s. Equation 14.9 can be used with this substitution. Hence the solution for exit concentration in the Laplace domain can be written (for a pulse input) as

\begin{matrix} {\bar{c}}_{e} = \frac{4 α exp (P e * / 2)}{{(1 + α)}^{2} exp (α P e * / 2) - {(1 - α)}^{2} exp (- α P e * / 2)} & (14.15) \end{matrix}

$\begin{matrix} {\bar{c}}_{e} = \frac{4 α exp (P e * / 2)}{{(1 + α)}^{2} exp (α P e * / 2) - {(1 - α)}^{2} exp (- α P e * / 2)} & (14.15) \end{matrix}$

where

α = \sqrt{(1 + 4 s / P e *)}

$α = \sqrt{(1 + 4 s / P e *)}$

The inversion, which is mathematically challenging, provides the time response, but it is easier to work with the moments, which are shown in the following paragraph. Of course one can use MATHEMATICA or MAPLE directly to generate the time domain results numerically as well.

14.3.2 Moments of the Response Curve

The first and second moment can be computed from the Laplace domain using the formulae shown in Section 13.4. The following results may be verified:

\begin{matrix} μ_{1}^{*} = 1 & (14.16) \end{matrix}

$\begin{matrix} μ_{1}^{*} = 1 & (14.16) \end{matrix}$

\begin{matrix} {σ *}^{2} = μ_{2}^{*} - μ_{1}^{* 2} = \frac{2}{P e *} - \frac{2}{{P e *}^{2}} (1 - exp (- P e *) & (14.17) \end{matrix}

$\begin{matrix} {σ *}^{2} = μ_{2}^{*} - μ_{1}^{* 2} = \frac{2}{P e *} - \frac{2}{{P e *}^{2}} (1 - exp (- P e *) & (14.17) \end{matrix}$

The dimensionless first moment is equal to one. Therefore the actual first moment is equal to the mean passage time.

The second central moment (scaled by the square of the mean passage time) is indicative of the dispersion coefficient. For large values of Pe* (reactors closer to plug flow) this reduces to

{σ *}^{2} = \frac{2}{P e *}

${σ *}^{2} = \frac{2}{P e *}$

If the reactor were modeled as a series of backmixed reactors (tanks in series model) instead of using the dispersion model, the dimensionless second moment would be

{σ *}^{2} = \frac{1}{N}

${σ *}^{2} = \frac{1}{N}$

This was shown in Example 13.1 in the last chapter.

Hence we find an equivalence between the two models. The number of tanks needed to model the system is approximately equal to Pe*/2. Hence either of the two models can be used and the prediction will be close if the second moments are matched.

Open-Open Boundary Conditions

The open-open boundary conditions are also used to analyze the tracer data. This type of approach is useful, for example, when the tracer is injected at some distance into the reactor. For example in a packed column, the tracer may be injected at a length equal to three or four packing diameters rather than right at the inlet. Similarly the tracer may be measured at some intermediate point near the exit rather than the actual exit. In this case there is dispersion on both the entrance side and the exit side and open-open boundary conditions are more suitable. A schematic of an open-open system is shown in Figure 14.2.

Figure 14.2 Schematic of open-open boundary conditions.

The moments are given by the following expressions for the open-open case:

μ_{1}^{*} = 1 + \frac{2}{P e *}

$μ_{1}^{*} = 1 + \frac{2}{P e *}$

{σ *}^{2} = \frac{2}{P e *} + \frac{8}{{P e *}^{2}}

${σ *}^{2} = \frac{2}{P e *} + \frac{8}{{P e *}^{2}}$

14.3.3 Time Domain Solution

Time domain solutions are lengthy and can be evaluated numerically. The analytical solution (Wen and Fan, 1975) for the (cross-sectional averaged) exit concentration is as follows for a pulse injection.

\begin{matrix} 〈 c_{A, e} 〉 (t^{*}) = \sum_{i = 1}^{\infty} \frac{2 λ_{n} (P e * sin (λ_{n}) + λ_{n} cos (λ_{n})}{({P e *}^{2} / 4 + P e * + λ_{n}^{2})} exp (Pe / 2) \times exp [- t * (\frac{{P e *}^{2} + λ_{n}^{2}}{P e *})] & (14.18) \end{matrix}

$\begin{matrix} 〈 c_{A, e} 〉 (t^{*}) = \sum_{i = 1}^{\infty} \frac{2 λ_{n} (P e * sin (λ_{n}) + λ_{n} cos (λ_{n})}{({P e *}^{2} / 4 + P e * + λ_{n}^{2})} exp (Pe / 2) \times exp [- t * (\frac{{P e *}^{2} + λ_{n}^{2}}{P e *})] & (14.18) \end{matrix}$

The λ_n are the eigenvalues, given as the roots of

2 \cot (λ) = \frac{λ}{P e *} - \frac{P e *}{4 λ}

$2 \cot (λ) = \frac{λ}{P e *} - \frac{P e *}{4 λ}$

It is interesting to note that for small deviations from plug flow (large Pe* values) the E-curve can be reduced to

\begin{matrix} 〈 c_{A, e} 〉 (t *) = E (t *) = \frac{1}{\sqrt{4 π {D *}_{E}}} exp [(\frac{- (1 - t *)^{2}}{4 {D *}_{E}})] & (14.19) \end{matrix}

$\begin{matrix} 〈 c_{A, e} 〉 (t *) = E (t *) = \frac{1}{\sqrt{4 π {D *}_{E}}} exp [(\frac{- (1 - t *)^{2}}{4 {D *}_{E}})] & (14.19) \end{matrix}$

This has the same form as the Gaussian (normal) distribution.

Illustrative results for the exit concentration for a step tracer are shown in Figure 14.3. The response is shown for a backmixed system, for Pe* values of 2 and 10, and for the case of plug flow (Pe* = ∞). The plug flow is a sharp step function placed at the mean residence time (t* = 1 in dimensionless units). For the case of Pe = 0, the response curve approaches the backmixed system. For other Pe values the response is spread on either side of the plug flow step function, approaching one for large values of time.

Graphical representation shows Tracer exit concentration versus time.

Figure 14.3 Tracer exit concentration versus time based on the dispersion model computed using the MATLAB PDEPE solver for a step input case.

14.4 Taylor Model for Dispersion in Laminar Flow

Taylor (1953) derived the classical result given by Equation 4.6 for the dispersion coefficient, D_E, of a solute for pipe flow under laminar flow conditions. This expression is derived here following Taylor’s analysis.

Consider a pulse of dye introduced into a liquid laminar flow as shown in Figure 14.4.

Diagrammatic representation of the concept of Taylor diffusion.

Three figures whose structures resemble a cylinder show the stages of Taylor diffusion. The first figure has a cylinder that is shown to contain a vertical bar labeled "Pulse of dye" at the left end. A set of rightward arrows from the right of the pulse of dye is shown to resemble a laminar flow representation. The figure is captioned "Pulse of dye." From this, an arrow indicates the flow to next stage of diffusion. The second figure has a cylinder with the vertical bar to have a deep dent on the right that resembles a U facing the left. Arrows from left and right arms of the U face toward the middle of U, the arrows resemble the turbulent flow. From this, an arrow indicates the flow to next stage of diffusion. The figure is captioned "Convection shears it." The third figure has a cylinder with its center position part filled with slant lines. The figure is captioned "Diffusion spreads it into a slug."

Figure 14.4 Illustration of the concept of Taylor diffusion: combined effect of axial convection and radial diffusion caues the pulse of dye to be spread with a mechanism similar to diffusion.

This pulse is sheared due to convection due to the variation of the velocity as a function of radial position. This creates a concentration gradient in the radial direction and causes the spread of the dye by diffusion. After some entry region, the dye is smeared into a slug and further on it appears that the dye is spreading on either side of the slug through a diffusion-type process. The process is sketched in Figure 14.4. The spreading of the pulse is called dispersion and is a combined effect of convection (due to a non-uniform velocity profile) and radial diffusion. The goal of the Taylor dispersion analysis is to derive an expression for the spread of the dye using a Fick’s law type of model for the dispersion process.

The starting point is the convection-diffusion model for Newtonian laminar flow studied in Chapter 10. We now add the time derivative in order to investigate the transient response. The resulting model for laminar flow is

\begin{matrix} \frac{\partial C_{A}}{\partial t} + 2 〈 υ 〉 (1 - ξ^{2}) \frac{\partial C_{A}}{\partial z} = \frac{D}{R^{2}} [\frac{1}{ξ} \frac{\partial}{\partial ξ} (ξ \frac{\partial C_{A}}{\partial ξ})] & (14.20) \end{matrix}

$\begin{matrix} \frac{\partial C_{A}}{\partial t} + 2 〈 υ 〉 (1 - ξ^{2}) \frac{\partial C_{A}}{\partial z} = \frac{D}{R^{2}} [\frac{1}{ξ} \frac{\partial}{\partial ξ} (ξ \frac{\partial C_{A}}{\partial ξ})] & (14.20) \end{matrix}$

Dimensional (actual) variables are used here except for the radial coordinate, which is represented by ξ, equal to r/R. The coordinate system can be transformed to moving coordinates as

z* = z – 〈v〉 t

and

t* = t

Here z* is the axial position in a coordinate system moving with the average velocity. The variable t* is the same time variable t but a different symbol is used to distinguish the two sets of independent variables in the two systems (stationary vs. moving). Also note that t* and z* here have the units of time and distance, respectively, and are not dimensionless in this section.

The partial derivatives in Equation 14.20 have to be transformed using the chain rule. The following results can be derived:

\frac{\partial C_{A}}{\partial t} = \frac{\partial C_{A}}{\partial t *} - 〈 υ 〉 \frac{\partial C_{A}}{\partial z *}

$\frac{\partial C_{A}}{\partial t} = \frac{\partial C_{A}}{\partial t *} - 〈 υ 〉 \frac{\partial C_{A}}{\partial z *}$

Using similar mathematical manipulations, you should verify that

\frac{\partial C_{A}}{\partial z} = \frac{\partial C_{A}}{\partial t *} \frac{\partial t *}{\partial z *} + \frac{\partial C_{A}}{\partial z *} \frac{\partial z *}{\partial z} = \frac{\partial C_{A}}{\partial z *}

$\frac{\partial C_{A}}{\partial z} = \frac{\partial C_{A}}{\partial t *} \frac{\partial t *}{\partial z *} + \frac{\partial C_{A}}{\partial z *} \frac{\partial z *}{\partial z} = \frac{\partial C_{A}}{\partial z *}$

since the term $\frac{\partial t *}{\partial z *}$ $\frac{\partial t *}{\partial z *}$ is zero and the term $\frac{\partial z *}{\partial z}$ $\frac{\partial z *}{\partial z}$ is one.

Hence the model in the moving reference frame is

\begin{matrix} \frac{R^{2}}{D} \frac{\partial C_{A}}{\partial t *} + \frac{〈 υ 〉 R^{2}}{D} [2 (1 - ξ^{2}) - 1] \frac{\partial C_{A}}{\partial z *} = \frac{1}{ξ} \frac{\partial}{\partial ξ} (ξ \frac{\partial C_{A}}{\partial ξ}) & (14.21) \end{matrix}

$\begin{matrix} \frac{R^{2}}{D} \frac{\partial C_{A}}{\partial t *} + \frac{〈 υ 〉 R^{2}}{D} [2 (1 - ξ^{2}) - 1] \frac{\partial C_{A}}{\partial z *} = \frac{1}{ξ} \frac{\partial}{\partial ξ} (ξ \frac{\partial C_{A}}{\partial ξ}) & (14.21) \end{matrix}$

The time derivative term can be dropped if t* > R²/D (the radial diffusion time). The interpretation is that after the time is greater than the radial diffusion time in a moving coordinate system, the system reaches a pseudo-steady state case with the convection term balancing the diffusion term. Referring to Figure 14.4, this means that the smearing of the tracer due to diffusion has already taken place (stage 3 of the figure). The corresponding distance will be 〈v〉 R²/D and the analysis will be valid if the observation point is larger than this length. Hence the Taylor analysis will hold if L/R is larger than 〈v〉 R/D.

In a moving reference frame $\frac{\partial C_{A}}{\partial z *}$ $\frac{\partial C_{A}}{\partial z *}$ is not expected to vary significantly and Taylor assumed this to be a constant. Let this constant be called $A$ $A$ :

\begin{matrix} A = \frac{\partial C_{A}}{\partial z *} = \frac{\partial < C_{A} >}{\partial z *} & (14.22) \end{matrix}

$\begin{matrix} A = \frac{\partial C_{A}}{\partial z *} = \frac{\partial < C_{A} >}{\partial z *} & (14.22) \end{matrix}$

< C_A > is the cross-sectional average concentration. Hence Equation 14.21 reduces to

\begin{matrix} (1 - 2 ξ^{2}) \frac{A < υ > R^{2}}{D} = \frac{1}{ξ} \frac{\partial}{\partial ξ} (ξ \frac{\partial C_{A}}{\partial ξ}) & (14.23) \end{matrix}

$\begin{matrix} (1 - 2 ξ^{2}) \frac{A < υ > R^{2}}{D} = \frac{1}{ξ} \frac{\partial}{\partial ξ} (ξ \frac{\partial C_{A}}{\partial ξ}) & (14.23) \end{matrix}$

This can be integrated twice with respect to ξ to obtain an approximate expression for the variation of the concentration as a function of dimensionless radial position. The result after applying the two boundary conditions of no flux at both the center and wall is

\begin{matrix} C_{A} = (\frac{ξ^{2}}{4} - \frac{ξ^{4}}{8}) \frac{A < υ > R^{2}}{D} + C_{0} & (14.24) \end{matrix}

$\begin{matrix} C_{A} = (\frac{ξ^{2}}{4} - \frac{ξ^{4}}{8}) \frac{A < υ > R^{2}}{D} + C_{0} & (14.24) \end{matrix}$

where C₀ is the unknown center line concentration.

Taking the cross-sectional average we have

\begin{matrix} < C_{A} > = \frac{1}{12} \frac{A < υ > R^{2}}{D} + C_{0} & (14.25) \end{matrix}

$\begin{matrix} < C_{A} > = \frac{1}{12} \frac{A < υ > R^{2}}{D} + C_{0} & (14.25) \end{matrix}$

Taking the flow average (cup-mixing average), we obtain

\begin{matrix} C_{Ab} = \frac{1}{16} \frac{A < υ > R^{2}}{D} + C_{0} & (14.26) \end{matrix}

$\begin{matrix} C_{Ab} = \frac{1}{16} \frac{A < υ > R^{2}}{D} + C_{0} & (14.26) \end{matrix}$

The difference may be expressed as

\begin{matrix} C_{Ab} = < C_{A} > - \frac{A < υ > R^{2}}{48 D} & (14.27) \end{matrix}

$\begin{matrix} C_{Ab} = < C_{A} > - \frac{A < υ > R^{2}}{48 D} & (14.27) \end{matrix}$

Multiplying by 〈v〉 and also substituting for $A$ $A$ as the derivative of the concentration ∂ < C_A > /∂z* as per Equation 14.22, we get the following result:

\begin{matrix} < υ > C_{Ab} = < υ > < C_{A} > - (\frac{1}{48} \frac{{〈 υ 〉}^{2} R^{2}}{D}) \frac{\partial < C_{A} >}{\partial z *} & (14.28) \end{matrix}

$\begin{matrix} < υ > C_{Ab} = < υ > < C_{A} > - (\frac{1}{48} \frac{{〈 υ 〉}^{2} R^{2}}{D}) \frac{\partial < C_{A} >}{\partial z *} & (14.28) \end{matrix}$

The first term can be viewed as the mass of A crossing any axial position (per unit cross-sectional area). The second term is the mass of A crossing computed using the mean (area-averaged) concentration. Hence the last term is the extra term and can be interpreted as a correction term. This term has the appearance of Fick’s law. The dispersion representation is

\begin{matrix} < υ > C_{Ab} = < υ > < C_{A} > - D_{E} \frac{\partial < C_{A} >}{\partial z *} & (14.29) \end{matrix}

$\begin{matrix} < υ > C_{Ab} = < υ > < C_{A} > - D_{E} \frac{\partial < C_{A} >}{\partial z *} & (14.29) \end{matrix}$

Comparing the last two equations, the following expression for D_E can be obtained:

\begin{matrix} \begin{matrix} D_{E} = \frac{1}{48} \frac{{〈 υ 〉}^{2} R^{2}}{D} \end{matrix} & (14.30) \end{matrix}

$\begin{matrix} \begin{matrix} D_{E} = \frac{1}{48} \frac{{〈 υ 〉}^{2} R^{2}}{D} \end{matrix} & (14.30) \end{matrix}$

This is the classical result obtained by Taylor for a dispersion coefficient in laminar flow. In a follow-up paper, Taylor (1954a) used the theory to measure molecular diffusivity of solutes present in a flowing stream and demarcated the conditions under which the diffusivity can be obtained. Although derived originally for laminar flow, the concept has been used in many applications, including chemical reactor analysis, and we have already seen an example of this for reactors; additional examples in separation processes, chromatography columns, and so on, are discussed later in the text.

14.5 Segregated Flow Model

Note that the Taylor dispersion model does not apply to short columns. The condition for validity of the Taylor model can be stated as

\frac{L}{d_{t}} > \frac{ReSc}{4}

$\frac{L}{d_{t}} > \frac{ReSc}{4}$

Normally this condition is difficult to fulfill for liquids where ReSc can be quite large. Very long pipes are needed for Taylor dispersion to be observed in such pipes. For gases this can be satisfied more easily since Sc is comparable to one.

For shorter pipes, the process is dominated by convection effects caused by variation of the axial velocity in the radial direction. The tracer response can be modeled in such cases by what is called the segregated flow model. The diffusion terms are dropped in this case and the convection balances the accumulation. The model equation (Equation 14.20) is now simplified as

\begin{matrix} \frac{\partial C_{A}}{\partial t} = - 2 〈 υ 〉 (1 - ξ^{2}) \frac{\partial C_{A}}{\partial z} & (14.31) \end{matrix}

$\begin{matrix} \frac{\partial C_{A}}{\partial t} = - 2 〈 υ 〉 (1 - ξ^{2}) \frac{\partial C_{A}}{\partial z} & (14.31) \end{matrix}$

The exit age distribution based on the solution of this equation can be derived and shown to be:

E (t) = {\begin{matrix} 0 & if t \leq \bar{t} / 2 where \bar{t} = L / 〈 υ 〉 \\ {\bar{t}}^{2} / t^{3} & if t \geq \bar{t} / 2 \end{matrix}

$E (t) = {\begin{matrix} 0 & if t \leq \bar{t} / 2 where \bar{t} = L / 〈 υ 〉 \\ {\bar{t}}^{2} / t^{3} & if t \geq \bar{t} / 2 \end{matrix}$

The model applies when the diffusion coefficient is small; that is, tracer spread is mainly caused by the difference in velocity at various radial locations. The tracer at the center moves faster and arrives at the exit at time equal to half the mean passage time, since the fluid moves twice the mean velocity at the center. No tracer will appear before that. Subsequently tracer at each location will spend a time equal to the local residence time at that radial position and arrive at the exit at that tine. The response curve is shown in Figure 14.5.

Graphical representation shows the response curve for Segregated Flow Model.

Figure 14.5 E-curve for laminar flow reactor under segregration. This model applies when the diffusion coefficient is small.

Both the dispersion and segregation models have their own range of applications. The model predictions for a reacting system are shown in Chapter 17 where a detailed analysis of a laminar flow reactor is provided. In that chapter the segregated model and the dispersion model are compared with a full 2-D differential model and the range of validity of each of these models is presented.

14.6 Dispersion Coefficient Values for Some Common Cases

Dispersion coefficient values for some common cases are presented in this section.

Pipe Flow of a Non-Newtonian Liquid. If the fluid behavior is given by a power law model, the following equation derived by Fan and Hwang (1965) can be used for the dispersion Peclet number:

P e * = \frac{2 (3 n + 1) (5 n + 1)}{n^{2}} \frac{\bar{t} D_{A}}{R^{2}}

$P e * = \frac{2 (3 n + 1) (5 n + 1)}{n^{2}} \frac{\bar{t} D_{A}}{R^{2}}$

Here n is the power law index. For n = 1, the coefficient above is 48, consistent with the Taylor model for a Newtonian fluid.

Axial Dispersion in Channel Flow. Consider pressure-driven laminar flow in a channel of height 2h. The following formula from which the axial dispersion coefficient can be derived closely follows the Taylor approach. Details are left as an exercise problem (14.16).

D_{E} = \frac{2 h^{2} {〈 υ 〉}^{2}}{105 D_{A}}

$D_{E} = \frac{2 h^{2} {〈 υ 〉}^{2}}{105 D_{A}}$

where 〈v〉 is the averaged velocity and D_A is the diffusivity of the species under consideration.

Axial Dispersion in Turbulent Flow. Taylor (1954b) showed that the following expression is suitable for the calculation of the axial dispersion coefficient for turbulent flow in a pipe:

D_E = 5d_tv_f

Here d_t is the pipe radius and v_f is the friction velocity. This is related to the friction factor by the following formula:

υ_{f} = 〈 υ 〉 \sqrt{f / 2}

$υ_{f} = 〈 υ 〉 \sqrt{f / 2}$

Using the Blasius equation for the friction factor, f = 0.0791Re^–1/4 for turbulent flow, we find

D_{E}^{*} \propto R e^{- 1 / 8}

$D_{E}^{*} \propto R e^{- 1 / 8}$

The above correlation predicts somewhat lower values than the experimental values. The following correlation proposed by Wen and Fan (1975) fits the data more closely:

D_{E}^{*} = \frac{3 \times 10^{7}}{R e^{2. 1}} + \frac{1.3 5}{R e^{1 / 8}}

$D_{E}^{*} = \frac{3 \times 10^{7}}{R e^{2. 1}} + \frac{1.3 5}{R e^{1 / 8}}$

The first term is the correction due to transitional flow and at high Reynolds numbers only the second term is important. Note that the Re to the power of –1/8 proportionality predicted by the Taylor model is retained.

Dispersion Coefficient in Packed Beds. Knowledge of axial dispersion in packed beds is of importance in many applications such as adsorber design, chromatographic separations, and so on, in addition to packed reactors. The axial dispersion coefficient is expressed in terms of a dimensionless parameter, the dispersion Peclet number, defined as

P e_{d}^{*} = \frac{ɛ_{B} υ_{z} d_{p}}{D_{E}}

$P e_{d}^{*} = \frac{ɛ_{B} υ_{z} d_{p}}{D_{E}}$

Note that the particle diameter is used as the length scale here. v_z is the superficial fluid velocity.

Two regimes can be identified: the molecular diffusion controlled regime and the hydrodynamic regime.

The molecular control holds for low values of ReSc. The dispersion coefficient is modeled using a torutosity factor:

D_E = D_A/τ

where the torutosity τ is taken as $\sqrt{2}$ $\sqrt{2}$ for packed beds; hence $D_{E} = D_{A} / \sqrt{2} = 0.707 D_{A}$ $D_{E} = D_{A} / \sqrt{2} = 0.707 D_{A}$ is suggested for this regime.

The hydrodynamic regime holds for high values of ReSc, a molecular Peclet number greater than two or so. Aris and Amundson (1957) showed that the dispersion Peclet number based on the particle diameter can be represented as

P e_{d}^{*} = \frac{2}{η}

$P e_{d}^{*} = \frac{2}{η}$

where η is a geometric parameter that is representative of distance between successive particle layers. For different arrangements of spherical particles, the range of values of η is between 0.817 and 1.0. Hence D*_E = 2u_gd_p may be used as an approximate formula in this range.

The equation was modified to include the Reynolds number dependency. The factor η was replaced by (1 – p)/p and the equation was modified to

P e_{d}^{*} = \frac{2 p}{1 - p}

$P e_{d}^{*} = \frac{2 p}{1 - p}$

where p is defined as

p = 0.17 + 0.33 exp(–24/Re)

For an intermediate regime, a combined correlation of the following form is useful for spherical particles:

\begin{matrix} \frac{1}{P e_{d}^{*}} = \frac{1 - p}{p} [Y + Y^{2} (exp [- Y^{- 1}] - 1)] + \frac{ɛ_{B}}{τ Re S c} & (14.32) \end{matrix}

$\begin{matrix} \frac{1}{P e_{d}^{*}} = \frac{1 - p}{p} [Y + Y^{2} (exp [- Y^{- 1}] - 1)] + \frac{ɛ_{B}}{τ Re S c} & (14.32) \end{matrix}$

where Y is defined as

Y = \frac{p (1 - p) ReSc}{23.16 (1 - ɛ_{B})}

$Y = \frac{p (1 - p) ReSc}{23.16 (1 - ɛ_{B})}$

A summary and a critical review of dispersion in packed beds is presented in Delgado (2006) and is useful for further evaluation of this parameter. The parametric effects of column to particle diameter, column length to particle diameter, fluid properties, and so on, are discussed in detail in this reference.

14.7 Two-Phase Flow: Models Based on Ideal Flow Patterns

Mesoscopic models for two-phase flow systems follow the developments shown in Section 4.3. The first modeling approach uses the ideal flow patterns, now for both phases. Then non-idealities to account for the deviation can be added. In the ideal contacting assumption, each phase may be assumed to be in either in plug flow or completely mixed in the ideal contacting assumption. Thus we get four combinations:

Gas and liquid both in plug flow
Gas and liquid both backmixed
Gas in plug flow and liquid backmixed
Gas backmixed and liquid in plug flow

The last case (gas backmixed but liquid in plug flow) is not very common in process equipment. Systems with batch liquid and continuous gas flow may be modeled using this contacting pattern. In any case the analysis of the fourth case is mathematically the same as the third with the fluids switched. The first two cases have been analyzed in earlier chapters. Here we discuss the third case and show how models for such systems can be formulated.

14.7.1 Plug-Backmixed Model

The case where gas is in plug flow and the liquid is backmixed is analyzed in the following section. Note that the discussion is not specific to gas–liquid systems and applies to any fluid–fluid system with one of the phases back-mixed and the other phase in plug flow. The schematic of the control volumes used in the analysis is shown in Figure 14.6.

Diagrammatic representation of a two-phase plug-backmixed system.

A large square block is divided into two segments by a dotted vertical line. The left segment is Gas plug flow and the right segment is Liquid backmixed. The bottom edge of the square is z equals 0 and the top edge of the square is z equals H. Both the segments have separate inlets (bottom) and outlets (top). The rate of flow of Gas in and Gas out is Q subscriptG, while the concentration of C subscript(AG, i) at the Gas in and at the Gas out concentration is C subscript(AG, e). The rate of flow of Liquid in and Liquid out is Q subscriptL, while the concentration of C subscript(AL, i) at the Liquid in and at the Liquid out concentration is C subscript(AL, e). A control volume inside the Gas segment of thickness delta z is shown to be enclosed by two horizontal lines. An arrow flows into the bottom horizontal line, while an arrow flows out from the top horizontal line. The segment is captioned "Transferred." An arrow flows from the control volume to the Liquid segment. The Liquid segment is captioned transferred to liquid is an integral average of the transfer rate from various z-positions.

Figure 14.6 Schematic of a two-phase plug-backmixed system showing the control volumes. For gas a differential volume is used while for liquid the entire liquid volume is used.

The control volume for the gas is mesoscopic and occupies a section Δz of the equipment in the flow direction. The control volume for the liquid is macroscopic and occupies the entire liquid volume in the system. Thus both meso and macro balances have to be used for the same problem.

The species mass balance in the gas phase balance leads to

- u_{G} \frac{d C_{AG}}{dz} - K_{L} a_{gl} (\frac{C_{AG}}{H_{A}} - C_{AL}) = 0

$- u_{G} \frac{d C_{AG}}{dz} - K_{L} a_{gl} (\frac{C_{AG}}{H_{A}} - C_{AL}) = 0$

u_G is the superficial gas velocity equal to Q_G/A. K_La_gl is the overall mass transfer coefficient based on the liquid driving force and H_A is the Henry constant expressed in concentration ratio.

The equation is made dimensionless by defining the dimensionless concentration as

c_{A G} (η) = \frac{C_{AG} (z)}{C_{AG, i}}

$c_{A G} (η) = \frac{C_{AG} (z)}{C_{AG, i}}$

η is the dimensionless location along the column height, defined as z/L.

For liquid we use the maximum solubility value as the reference concentration. Thus we use C_AG,i/H_A as the reference and define the dimensionless exit liquid concentration as

c_{A L, e} = \frac{C_{AL, e}}{C_{AG, i} / H_{A}}

$c_{A L, e} = \frac{C_{AL, e}}{C_{AG, i} / H_{A}}$

The gas phase balance is then

\begin{matrix} - \frac{{d c}_{A G}}{dη} - \frac{κ_{L}}{Λ_{gl}} (c_{A G} - c_{A L, e}) = 0 & (14.33) \end{matrix}

$\begin{matrix} - \frac{{d c}_{A G}}{dη} - \frac{κ_{L}}{Λ_{gl}} (c_{A G} - c_{A L, e}) = 0 & (14.33) \end{matrix}$

Here κ_L is a dimensionless mass transfer coefficient:

κ_{L} = \frac{K_{L} a_{gl} V_{R}}{Q_{L}}

$κ_{L} = \frac{K_{L} a_{gl} V_{R}}{Q_{L}}$

Λ_gl is a flow ratio parameter (corrected by the Henry coefficient):

Λ_{gl} = \frac{H_{A} Q_{G}}{Q_{L}}

$Λ_{gl} = \frac{H_{A} Q_{G}}{Q_{L}}$

The liquid phase balance can be formulated as

Q_{L} (C_{AL, i} - C_{AL, e}) + K_{L} a_{gl} \int_{0}^{H} (\frac{C_{AG}}{H_{A}} - C_{AL, e}) Adz = 0

$Q_{L} (C_{AL, i} - C_{AL, e}) + K_{L} a_{gl} \int_{0}^{H} (\frac{C_{AG}}{H_{A}} - C_{AL, e}) Adz = 0$

Note how the mass transfer rate term from gas to liquid is written as an integral. Locally the driving force is therefore $\frac{C_{AG}}{H_{A}} - C_{AL, e}$ $\frac{C_{AG}}{H_{A}} - C_{AL, e}$ . Here C_AL,e is the exit liquid concentration, which is a constant, but C_AG, the gas concentration, is a function of z. Hence a local differential volume AΔz is used to find the local rate of transfer. The integral of this provides the total transferred from the gas to the liquid.

The liquid phase balance in dimensionless variables is

\begin{matrix} c_{A L, i} - c_{A L, e} + κ_{L} \int_{0}^{1} (c_{A G} (η) - c_{A L, e}) dη = 0 & (14.34) \end{matrix}

$\begin{matrix} c_{A L, i} - c_{A L, e} + κ_{L} \int_{0}^{1} (c_{A G} (η) - c_{A L, e}) dη = 0 & (14.34) \end{matrix}$

The solution is straightforward but consists of several algebraic steps. Equation 14.33 can be integrated to get the profiles in the gas phase:

\begin{matrix} c_{A G} - c_{A L, e} = (1 - c_{A L, e}) exp (- η \frac{κ_{L}}{Λ_{gl}}) & (14.35) \end{matrix}

$\begin{matrix} c_{A G} - c_{A L, e} = (1 - c_{A L, e}) exp (- η \frac{κ_{L}}{Λ_{gl}}) & (14.35) \end{matrix}$

This can then be used to find the integral term in the liquid mass balance:

\int_{0}^{1} (c_{A G} (η) - c_{A L, e}) dη = (1 - c_{A L, e}) \frac{Λ_{gl}}{κ_{L}} ε

$\int_{0}^{1} (c_{A G} (η) - c_{A L, e}) dη = (1 - c_{A L, e}) \frac{Λ_{gl}}{κ_{L}} ε$

The term ε is defined as

ε = 1 – exp(– κ_L/Λ_gl)

Using this in Equation 14.34 and rearranging, we obtain the exit liquid concentration in an explicit form:

c_{A L, e} = \frac{c_{A L, i} + Λ_{gl} ε}{1 + Λ_{gl} ε}

$c_{A L, e} = \frac{c_{A L, i} + Λ_{gl} ε}{1 + Λ_{gl} ε}$

The corresponding exit gas concentration is given as

c_{A G, e} = \frac{{ε c}_{A L, i} + 1 + Λ_{gl} ε - ε}{1 + Λ_{gl} ε}

$c_{A G, e} = \frac{{ε c}_{A L, i} + 1 + Λ_{gl} ε - ε}{1 + Λ_{gl} ε}$

For large mass transfer coefficients, ε tends to one and the model reduces to the equilibrium model:

c_{AL, e}^{*} = \frac{c_{A L, i} + Λ_{gl}}{1 + Λ_{gl}}

$c_{AL, e}^{*} = \frac{c_{A L, i} + Λ_{gl}}{1 + Λ_{gl}}$

The model finds application in many areas, for example, in the calculation of tray efficiency in a distillation column, for simulation of fluid bed reactors, and for gas absorption in well-mixed continuous flow bubble columns. Some of these are illustrated as exercise problems at the end of this chapter.

Having considered three ideal contacting patterns, we now look at how non-idealities can be modeled using the dispersion concept.

14.7.2 Non-Idealities in Two-Phase Flow

In this section we show how deviations from the ideal contacting can be modeled using the dispersion concept. First we show some cases where it is required to consider these deviations from ideal flow patterns. The following guidelines are useful in this regard:

If the solute concentration changes by large amount, say 99% removal, then dispersion effects need to be considered.
If the system has a relativly low HTU, which means a relatively short contactor can achieve significant separation, then dispersion effects are important. Since the contactor is short, the dispersion Peclet number is small and plug flow may not be a good assumption.
When large eddies or circulation patterns develop in the system, for example, a bubble column absorber, the system can be modeled using the dispersion model. But the tanks in series model (the same as the mixing cell model) is closer to the physical picture and is preferred.
When there is a wide range of drop size in a gravity-driven liquid–liquid separation unit, the plug flow may not be suitable due to varying velocity of the drops and some drop phase backflow in the separator.
When there is a very large or very small flow ratio there is likely flow segregation and non-ideal contacting models should be used.
When there is significant channeling, e.g., due to inhomogeneity in packing near the wall, the flow pattern is again non-ideal. This is often important in small laboratory reactors. Here the wall region is comparable to the size of the reactor and bypassing can occur. A dispersion model may not be a good representation when bypassing occurs. Data in such systems should be used with caution when scaling up the reactor.

The model in the following section is based on the assumption that both phases are in dispersed plug flow. This covers a wide range of mixing and the four ideal cases can be derived as special cases by putting either a very small or very large value for the dispersion coefficient for each of the phases.

We also use dilute systems for simplicity, that is, the gas and the liquid flow rates are nearly constant. A linear equilibrium model is also used. Formulation is shown for both cocurrent and countercurrent flow although the models are similar with some minor switches.

Concurrent Flow

The model equations consist of the gas phase balance and the liquid phase balance for the solute in each phase.

For the gas phase, the following equation can be derived starting from the species mass balance:

\begin{matrix} D_{EG} \frac{d^{2} C_{AG}}{d x^{2}} - u_{G} \frac{d C_{AG}}{dz} - K_{L} a_{gl} (\frac{C_{AG}}{H_{A}} - C_{AL}) = 0 & (14.36) \end{matrix}

$\begin{matrix} D_{EG} \frac{d^{2} C_{AG}}{d x^{2}} - u_{G} \frac{d C_{AG}}{dz} - K_{L} a_{gl} (\frac{C_{AG}}{H_{A}} - C_{AL}) = 0 & (14.36) \end{matrix}$

The three terms represent the dispersion, convection, and mass transfer from gas to liquid in that order. D_EG is the dispersion coefficient in the gas phase and u_G is the superficial gas velocity.

Liquid phase mass balance is given by the following equation:

\begin{matrix} D_{EL} \frac{d^{2} C_{AL}}{d x^{2}} - u_{L} \frac{d C_{AL}}{dz} + K_{L} a_{gl} (\frac{C_{AG}}{H_{A}} - C_{AL}) = 0 & (14.37) \end{matrix}

$\begin{matrix} D_{EL} \frac{d^{2} C_{AL}}{d x^{2}} - u_{L} \frac{d C_{AL}}{dz} + K_{L} a_{gl} (\frac{C_{AG}}{H_{A}} - C_{AL}) = 0 & (14.37) \end{matrix}$

The three terms represent the dispersion, convection, and transfer from gas to liquid in that order. The transfer term is common to the gas phase balance but now appears with the opposite sign. D_EL is the dispersion coefficient in the gas phase and u_L is the superficial gas velocity.

Boundary conditions, usually of the Danckwerts type, are applied to each of the phases. If the dispersion terms are dropped we get the model for plug flow of both phases.

The equations can be made dimensionless by introduction of the following parameters:

Dimensionless distance, $η = \frac{z}{L}$ $η = \frac{z}{L}$
Dimensionless gas phase concentration, $c_{A G} = \frac{C_{AG}}{C_{AG, i}}$ $c_{A G} = \frac{C_{AG}}{C_{AG, i}}$
Dimensionless liquid phase concentration, $c_{A L} = \frac{C_{AL}}{(C_{Ag, i} / H_{A})}$ $c_{A L} = \frac{C_{AL}}{(C_{Ag, i} / H_{A})}$

Note that the liquid concentration is scaled by the saturation value corresponding to the inlet gas concentration. The liquid concentration then varies from 0 to 1. Gas concentration is scaled by its inlet value and goes from 0 to 1 as well. These normalizations lead to the dimensionless version of the model:

\begin{matrix} \frac{1}{{P e}_{G}} \frac{d^{2} c_{A G}}{d η^{2}} - \frac{{d c}_{A G}}{dη} - \frac{κ_{gl}}{Λ_{gl}} (c_{A G} - c_{A L}) = 0 & (14.38) \end{matrix}

$\begin{matrix} \frac{1}{{P e}_{G}} \frac{d^{2} c_{A G}}{d η^{2}} - \frac{{d c}_{A G}}{dη} - \frac{κ_{gl}}{Λ_{gl}} (c_{A G} - c_{A L}) = 0 & (14.38) \end{matrix}$

\begin{matrix} \frac{1}{{P e}_{L}} \frac{d^{2} c_{A L}}{d x^{2}} - \frac{{d c}_{A L}}{dz} + κ_{gl} (c_{A G} - c_{A L}) = 0 & (14.39) \end{matrix}

$\begin{matrix} \frac{1}{{P e}_{L}} \frac{d^{2} c_{A L}}{d x^{2}} - \frac{{d c}_{A L}}{dz} + κ_{gl} (c_{A G} - c_{A L}) = 0 & (14.39) \end{matrix}$

The dimensionless parameters appearing in this equation are as follows:

Dispersion Peclet number for the gas phase, ${P e}_{G} = \frac{u_{G} L}{D_{EG}}$ ${P e}_{G} = \frac{u_{G} L}{D_{EG}}$
Dispersion Peclet number for the liquid phase ${P e}_{L} = \frac{u_{L} L}{D_{EL}}$ ${P e}_{L} = \frac{u_{L} L}{D_{EL}}$
Dimensionless mass transfer coefficient, $κ_{gl} = \frac{K_{L} a_{gl} L}{u_{L}}$ $κ_{gl} = \frac{K_{L} a_{gl} L}{u_{L}}$
Flow ratio parameter, $Λ_{gl} = \frac{u_{G} H_{A}}{u_{L}}$ $Λ_{gl} = \frac{u_{G} H_{A}}{u_{L}}$

Thus four parameters are needed to characterize the separator performance.

The Danckwerts boundary conditions in dimensionless form are used at the entrance and exit and these are as follows.

For the gas phase, the boundary conditions are

\begin{matrix} \begin{matrix} η = 0, & gas inlet, c_{A G} - \frac{1}{{P e}_{G}} \frac{{d c}_{A G}}{d η} = 1 \end{matrix} & (14.40) \end{matrix}

$\begin{matrix} \begin{matrix} η = 0, & gas inlet, c_{A G} - \frac{1}{{P e}_{G}} \frac{{d c}_{A G}}{d η} = 1 \end{matrix} & (14.40) \end{matrix}$

and

\begin{matrix} \begin{matrix} η = 1, & gas exit, \frac{{d c}_{A G}}{d η} = 0 \end{matrix} & (14.41) \end{matrix}

$\begin{matrix} \begin{matrix} η = 1, & gas exit, \frac{{d c}_{A G}}{d η} = 0 \end{matrix} & (14.41) \end{matrix}$

For the liquid phase the boundary conditions are

\begin{matrix} \begin{matrix} η = 0, & liquid inlet, c_{A L} - \frac{1}{P e *} \frac{{d c}_{A L}}{d η} = c_{A L, i} \end{matrix} & (14.42) \end{matrix}

$\begin{matrix} \begin{matrix} η = 0, & liquid inlet, c_{A L} - \frac{1}{P e *} \frac{{d c}_{A L}}{d η} = c_{A L, i} \end{matrix} & (14.42) \end{matrix}$

and

\begin{matrix} \begin{matrix} η = 1, & liquid exit, \frac{{d c}_{A L}}{d η} = 0 \end{matrix} & (14.43) \end{matrix}

$\begin{matrix} \begin{matrix} η = 1, & liquid exit, \frac{{d c}_{A L}}{d η} = 0 \end{matrix} & (14.43) \end{matrix}$

Model equations can be solved numerically with minor changes in the code given in Listing 14.1. The model is useful to predict the effect of non-ideality in separator. It can also be used for two-phase reactor models by adding the reaction term.

Countercurrent Flow

The dispersion model for countercurrent flow is similar to cocurrent flow with some minor modifications. The gas phase equation and the boundary conditions are the same.

But for the liquid phase a change in sign in the convection term is needed as the flow direction is now opposite to that of the gas. The corresponding equations in dimensionless form are as follows:

\begin{matrix} \frac{1}{{P e}_{L}} \frac{d^{2} c_{A L}}{d x^{2}} + \frac{{d c}_{A L}}{dz} + κ_{gl} (c_{A G} - c_{A L}) = 0 & (14.44) \end{matrix}

$\begin{matrix} \frac{1}{{P e}_{L}} \frac{d^{2} c_{A L}}{d x^{2}} + \frac{{d c}_{A L}}{dz} + κ_{gl} (c_{A G} - c_{A L}) = 0 & (14.44) \end{matrix}$

The boundary conditions are also switched and now read as

\begin{matrix} \begin{matrix} η = 1, & liquid inlet, c_{A L} + \frac{1}{{P e}_{L}} \frac{{d c}_{A L}}{d η} \end{matrix} = c_{A l, i} & (14.45) \end{matrix}

$\begin{matrix} \begin{matrix} η = 1, & liquid inlet, c_{A L} + \frac{1}{{P e}_{L}} \frac{{d c}_{A L}}{d η} \end{matrix} = c_{A l, i} & (14.45) \end{matrix}$

and

\begin{matrix} \begin{matrix} η = 0, & liquid exit, \frac{{d c}_{A L}}{d η} \end{matrix} = 0 & (14.46) \end{matrix}

$\begin{matrix} \begin{matrix} η = 0, & liquid exit, \frac{{d c}_{A L}}{d η} \end{matrix} = 0 & (14.46) \end{matrix}$

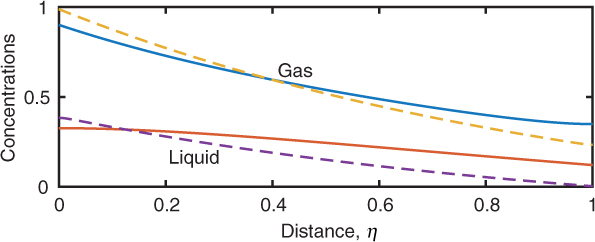
Since the problem is linear it can be solved by analytical methods. Pratt (1975) solved the problem analytically and presented results for the concentration profiles. Nowadays it is easier and more convenient to solve this numerically. Listing 14.1 is applicable simply by changing some terms. An illustrative result is shown in Figure 14.7.

Graphical illustration of the result of Countercurrent flow system model.

Figure 14.7 Effect of dispersion on the concentration profiles in a gas–liquid absorber; the dotted line is plug flow. The parameters used for the dispersion case are κ_gl = 1, Λ_gl = 0.5, Pe_G = 10, and Pe_L = 5.

The system behavior for the plug-plug flow case is generated by simply using large enough values of the Peclet parameters. Similarly the results for a backmix-backmix case can be simulated by setting Pe to a small value. Hence the dispersion model is flexible to handle the limiting cases. These limiting cases are shown in Table 14.2 for high and low values of the disperison coeficients in the gas and liquid phases.

Table 14.2 Ideal Contacting Patterns for Fluid–Fluid Systems

	Small D_EL	Large D_EL
Small D_EG	plug-plug	plug-backmixed
Large D_EG	backmixed-plug	backmixed-backmixed

Tanks in Series Model

The tanks in series model presented in Chapter 13 is an alternative method to handle non-idealities in two-phase flow. Each phase is represented by N tanks connected in series. If N = 1, a backmixed model is obtained. Similarly a large value of N simulates a plug flow case. Both dispersion and the tanks in series models show similar trends provided the parameters are matched to maintain similar second central moments. Often the choice is therefore the preference of the modeler.

The tanks in series model is preferable if there is a large extent of back-mixing, for example, a bubble column type of reactor. The dispersion is more useful for tall columns that are closer to plug flow, such as a packed bed absorber. One minor difficulty with the tanks in series model is that the number of tanks to be used for the liquid phase can be different from that for the gas phase. This can create some problems in coupling the two balances.

14.8 Tracer Response in Two-Phase Systems

In order to use the dispersion model shown in the last section, the dispersion coefficients for both phases have to be experimentally determined and the tracer methods used for single-phase systems are again useful. However, there are some caveats that have to be kept in mind and properly addressed in the interpretation of the tracer data.

The tracer may not stay in the same phase where it was introduced and may be transferred to the second phase. The overall response is then modulated by transport to the other phase. The observed tracer response can in such case show a dispersion effect even if the phase into which the tracer was introduced was in plug flow. Hence the tracer data cannot be interpreted as a single-phase system model and the effect of interphase mass transfer may need to be considered. Only if the tracer stays in the same phase where it was introduced will the response curve be a true representation of the backmixing in that phase. We will show some examples to illustrate the effects qualitatively. Key references are also cited for those interested in following this industrially important and relevant topic further.

First we consider a two-phase system with only one flowing phase, that is, gas–solid or liquid–solid systems. The effect of mass transfer on the tracer response is more readily visualized by looking at this simple example. Then we show the considerations needed for systems with two flowing phases.

14.8.1 Single Flowing Phase

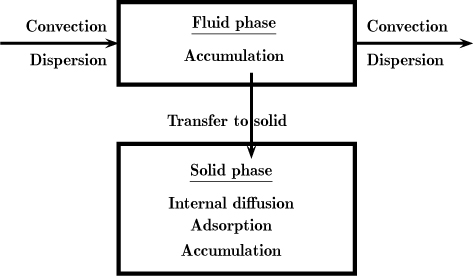
Consider a single flowing phase in contact with a solid that can adsorb some gas. Models for such systems are important in the design of packed bed adsorption columns and are treated in more detail in Chapter 29. Here we show how the tracer response is modified by the processes taking place in the solid phase. A schematic of the processes taking place in the gas and solid phases is shown in Figure 14.8.

Diagrammatic representation showing the mesoscopic model of the processes taking place in the gas and solid phases.

Figure 14.8 Schematic of processes in a mescoscopic control volume of a gas–solid adsorption column.

A simplified analysis is presented that assumes the gas is in plug flow and the process is in equilibrium at each point in the column. Thus the balance equation is

in at z – out at z + Δz – transferred to solid = accumulation

In mathematical form the gas phase balance is

u_{G} \frac{d C_{A}}{dz} = - k_{ex} (C_{A} - q_{A} / K_{A}) + ɛ_{B} \frac{\partial C_{A}}{\partial t}

$u_{G} \frac{d C_{A}}{dz} = - k_{ex} (C_{A} - q_{A} / K_{A}) + ɛ_{B} \frac{\partial C_{A}}{\partial t}$

where k_ex is the volumetric transfer coefficient from gas to the solid. Here q_A is the concentration in the second phase and K_A is the adsorption coefficient of the gas in the solid.

The balance on the second phase (solid) leads to

Accumulation = transfer from gas

The mathematical formulation of this is

(1 - ɛ_{B}) \frac{d q_{A}}{dt} = k_{ex} (C_{A} - q_{A} / K_{A})

$(1 - ɛ_{B}) \frac{d q_{A}}{dt} = k_{ex} (C_{A} - q_{A} / K_{A})$

The two equations can be combined to give

\begin{matrix} [ɛ_{B} \frac{\partial C_{A}}{\partial t} + (1 - ɛ_{B})] \frac{\partial q_{A}}{\partial t} = - u_{G} \frac{\partial C_{A}}{\partial x} & (14.47) \end{matrix}

$\begin{matrix} [ɛ_{B} \frac{\partial C_{A}}{\partial t} + (1 - ɛ_{B})] \frac{\partial q_{A}}{\partial t} = - u_{G} \frac{\partial C_{A}}{\partial x} & (14.47) \end{matrix}$

and this eliminates the transfer term.

If the mass transfer is rapid and equilibrium exists at every location in the column then

q_A = K_AC_A

Hence Equation 14.47 can be reduced to a single equation for the gas phase response:

\begin{matrix} [ɛ_{B} + K_{A} (1 - ɛ_{B})] \frac{{\partial c}_{A}}{\partial t} = u_{G} \frac{\partial C_{A}}{\partial z} & (14.48) \end{matrix}

$\begin{matrix} [ɛ_{B} + K_{A} (1 - ɛ_{B})] \frac{{\partial c}_{A}}{\partial t} = u_{G} \frac{\partial C_{A}}{\partial z} & (14.48) \end{matrix}$

This is the equation for the tracer response. The model is similar to a single-phase plug flow except for the coefficient term in the time derivative, known as the capacity term. This term now includes the adsorption constant. It is now larger by a factor of K_A(1 – ∊_B). The tracer will exist after a time L/u_G times ∊_B + K_A(1 – ∊_B) rather than at the mean passage time in the gas phase.

The first moment can be readily found from Equation 14.48 as

μ_{1} = \frac{L}{υ_{G}} [1 + \frac{1 - ɛ_{B}}{ɛ_{B}} K_{A}]

$μ_{1} = \frac{L}{υ_{G}} [1 + \frac{1 - ɛ_{B}}{ɛ_{B}} K_{A}]$

where v_G = u_G/∊_G, the interstitial velocity. The second moment is zero.

Effect of Internal Diffusion

If the solid is porous, part of the tracer will diffuse into the solid and the internal diffusion will add a further time delay. Similarly any axial dispersion in the gas phase will again add to the tracer spread. The second moment will no longer be zero. Including all these factors the second moment can be shown to be

\begin{matrix} μ_{2} = [\frac{2}{P e *} - \frac{2}{{P e *}^{2}} (1 - exp (- P e *)]] μ_{1}^{2} + \frac{6 (1 - ε_{B})}{u_{G}} {(ε_{p} + K_{A})}^{2} (\frac{1}{45 D_{e}} + \frac{1}{9 k_{s l} R}) & (14.49) \end{matrix}

$\begin{matrix} μ_{2} = [\frac{2}{P e *} - \frac{2}{{P e *}^{2}} (1 - exp (- P e *)]] μ_{1}^{2} + \frac{6 (1 - ε_{B})}{u_{G}} {(ε_{p} + K_{A})}^{2} (\frac{1}{45 D_{e}} + \frac{1}{9 k_{s l} R}) & (14.49) \end{matrix}$

which was derived by Schneider and Smith (1968). We find that the tracer response is affected by a number of factors in addition to the backmixing in the gas phase (Pe* parameter). Hence interpretation of tracer data has to include the effect of the additional contribution to the tracer spread.

14.8.2 Two Flowing Phases

If there are two flowing phases, the tracer can be introduced in either the gas phase or the liquid phase. The tracer can appear in the outlet of both phases as a result of mass transfer, even when it is introduced in only one of the phases. This can cause problems in data interpretation since the outlet response is not entirely due to dispersion. Tracer spread is due to dispersion only if the tracer stays in the same phase where it was introduced, for example. a liquid phase tracer such as NaCl that stays entirely in the liquid or a relatively non-volatile tracer in general. Similarly for a tracer introduced in the gas phase, the solubility of the gas has to be rather low in the liquid so that it stays mostly in the gas. Helium is often used as a tracer for such cases. Other gases have reasonable solubility and the interpretation of the tracer data is difficult since it is a function of not only the dispersion coefficient but also the mass transfer coefficient. It is also a function of the mixing pattern in the liquid.

The effect of tracer mass transfer effects can be examined by looking at the zeroth moment of the tracer response. For a tracer introduced in the gas phase we can define the zeroth moment for both the gas and the liquid phase:

μ_{0 G} = \int_{0}^{\infty} C_{AG, e} (t) dt

$μ_{0 G} = \int_{0}^{\infty} C_{AG, e} (t) dt$

and

μ_{0 L} = \int_{0}^{\infty} C_{AL, e} (t) dt

$μ_{0 L} = \int_{0}^{\infty} C_{AL, e} (t) dt$

Thus the zeroth moment of the tracer in the liquid phase can be non-zero although the tracer was introduced in the gas phase. Some tracer may undergo mass transfer to liquid and appear in the liquid exit stream. These considerations have to be included in the analysis of tracer response in two-phase systems.

The two zeroth moments are related by an overall mass balance requirement, which then leads to

Q_Gμ₀_G + Q_Lμ₀_L = $M$ $M$

where $M$ $M$ is the quantity of tracer introduced in the inlet stream of the gas phase.

Detailed analysis was undertaken by Ramachandran and Smith (1979) who showed that the zeroth moment is a function of the dimensionless parameters k_gl and Δ_gl. It also depends on whether two phases are flowing in a concurrent or countercurrent mode and what the level of mixing is in the liquid phase. Hence interpretation of tracer data in two-phase systems is prone to a number of assumptions and has to be handled with care. This could also possibly be the reason for the wide discrepancy seen in the literature for the reported dispersion coefficients even when experiments were done under very similar conditions.

Summary

Mesoscopic models are useful when there is significant variation in concentration in one direction, the flow direction, while the variation in the direction normal to flow is relatively small. Examples where such models are used are tubular reactors, packed bed catalytic reactors, packed bed absorption columns, countercurrent extraction columns, chromatographic columns, and so on.
In the mesoscopic model cross-flow concentration variations are not modeled and represented by average values. Note that two types of average concentrations arise upon the cross-sectional average of differential models: the flow-weighted average or the cup-mixing average and the cross-sectional average.
The convection terms are dependent on the flow-weighted average while the generation (and accumulation) term is based on the cross-sectional average. This leads to a closure problem unless the two are nearly equal.
The concept of plug flow is an idealized representation of the cross-direction concentration profile in the reactor. The assumption is that there is no concentration gradient in this direction, that is, the concentration is constant across any cross-section. Hence the cup-mixed value is the same as the cross-sectional average and no additional closure is needed.
Plug flow is a reasonable assumption for a nearly flat velocity profile, moderate or slow rate of reaction, no significant radial temperature profile, and no mass transfer to the wall.
Plug flow models can be corrected by introducing some dispersion leading to the axial-dispersed plug flow model. The concept of dispersion arises by connecting the cup mixing and the cross-sectional flux through a Fick’s law type of model.
The dispersion Peclet number is the important dimensionless group that determines the reactor performance in this model. This can be predicted from theory for simple flows such as laminar flow in long tubes as shown in the pioneering work of Taylor. In general this is a fitted parameter based on experimental data.
Dispersion effects are important in many applications other than separator and reactor modeling, for example, transport of pollutants in the environment, pharmacokinetics, chromatography, and so on; dispersion effects are used in modeling such processes.
Tracer experiments are widely used to characterize the non-ideal flow pattern in the reactors and the dispersion coefficient can be determined by matching the experimental tracer response with theory. The moments method is a simple and useful way of interpreting the data. In particular the dimensionless variance of the tracer (second central moment) can be related to the Peclet number.
A significant extent of non-idealities can be caused by bypassing dead zones and recirculation zones in some types of reactors. For such cases, the dispersion model may not be suitable for interpretation of data. The variance can be larger than one in such cases and these are referred to as non-ideal ill-behaved systems. Phenomenological models linking the various flow regions (similar to compartmental models discussed in the last chapter) are more useful in such cases. The tracer response can be used to find the parameters needed in such models.
Reactor behavior can be bracketed between plug flow and backmixed flow when the variance is less than one (non-ideal but well-behaved systems). The tanks in series model or the dispersion model can be used and provide similar predictions if the model parameter (number of tanks in one case, dispersion Peclet number in the other cases) is matched with the variance of the tracer response curve. However, reactor behavior can be smaller than even the backmix reactor for the non-ideal ill-behaved systems and therefore it cannot be bracketed between the two ideal flow patterns in such cases. An example is the fluid bed reactor.
Two-phase systems can be modeled by using a dispersion parameter for each of these phases. An alternative way of modeling such systems is the tanks in series model. The dispersion effects in separators can be assessed by the MATLAB code shown in the text. For low dispersion values the phase may be assumed to be in plug flow and vice versa. This leads to the four ideal contacting patterns shown in Table 14.2 for two-phase systems.
Tracer experiments in fluid–solid systems need to be interpreted by consideration of what is happening to the tracer in the solid phase. The internal diffusion within the particle can cause a spread in the tracer although the fluid phase itself may be in plug flow. Similarly the mean residence time is increased if the tracer adsorbs significantly in the particle. Hence the second moment of the tracer depends on many parameters (see Equation 14.49) in addition to the gas dispersion. The data interpretation needs an estimate of the adsorption constant, internal diffusion coefficient, and in some cases the fluid–solid mass transfer coefficient as well. Hence the measured data may not be representative of the true gas phase non-idealities.
Tracer methods are still useful for systems with two flowing phases for determining the extent of backmixing in each of the phases. However, the nature of the tracer becomes important and the true extent of mixing can be determined only if the tracer stays in the same phase where it was injected. In other cases, the tracer response needs to be corrected for the mass transfer term to account for the interfacial mass transfer. Thus a part of the tracer introduced in the gas phase may appear in the liquid phase and vice versa. Interpretation of such tracer data requires an estimate of the mass transfer rate between the two phases and is therefore prone to inaccuracies.

Review Questions

14.1 What is meant by the plug flow assumption?

14.2 What closure is accomplished by using the concept of dispersion?

14.3 State conditions when the plug flow model may be reasonably used.

14.4 Can the conversion in a reactor be less than that predicted by the backmixed assumption?

14.5 What are Danckwerts boundary conditions?

14.6 State the difference between closed-closed and open-open boundaries.

14.7 Is the mean residence time equal to the first moment for an open-open boundary?

14.8 For low values of D_E state the expression for the dimensionless variance of a tracer curve.

14.9 Explain why the dispersion coefficient is inversely proportional to the molecular diffusion coefficient.

14.10 State an approximate formula that relates the dispersion Peclet number to the number of tanks in series needed to model the same reactor.

14.11 List different models for accounting for deviation from plug flow in a two-phase contactor.

14.12 Define the four dimensionless parameters needed to model a separator using a dispersion model for both phases.

14.13 Why is the interpretation data in a packed bed with an adsorbing tracer more difficult than that for a non-adsorbing tracer?

14.14 What are the additional problems in interpreting tracer data in systems with two flowing phases compared to single-phase flow?

Problems

14.1 Plug flow reactor with variable velocity. When the velocity is changing in the system, show that the plug model can be written as

- \frac{d N_{Az}}{dz} = k_{1} < C_{A} >

$- \frac{d N_{Az}}{dz} = k_{1} < C_{A} >$

Here N_A is the moles of A crossing at z per unit area per unit time. The concentration terms can be related to the total molar flux, ${\tilde{V}}_{M} N_{A} / N_{t}$ ${\tilde{V}}_{M} N_{A} / N_{t}$ , where ${\tilde{V}}_{M}$ ${\tilde{V}}_{M}$ is the local molar volume of the mixture. This sets up all the equations in terms of N_A, N_B, and so on, and accounts for the variation in velocity along the length. A thermodynamic equation of state is needed to calculate the molar volume given the mixture composition.

Apply this to the following problem of acetaldehyde decomposing to methane and CO in a plug flow reactor operated at 793 K and 101 kPa pressure. The reaction is irreversible but second order with a rate constant of 0.43 m³/mol s; the feed to the reactor is 0.1 kg/sec. Simulate using ODE45 and plot the concentration profile of acetaldehyde along the reactor length.

14.2 Analytical solution for a first-order reaction with dispersion. Verify Equation 14.9 by finding the roots of the characteristic polynomials of the governing differential equation (Equation 14.6) and then using the Danckwerts boundary conditions.

14.3 Conversion for a first-order reaction based on dispersion model. A first-order reaction has rate constant of 3.33 × 10^–3 s^–1 and is carried out in a tubular reactor of length 3 m and a velocity of 1 m/s. The dispersion coefficient was measured by tracer experiments and found to have a value of 0.2 m²/s. Find the conversion in the reactor. Determine the deviation from the plug flow value.

14.4 From meso to macro. Macroscopic models result from mesoscopic models by averaging over the reactor length. Start with the meso-model given by Equation 14.1, which is repeated here for ease of reference:

\begin{matrix} - 〈 υ 〉 \frac{d C_{Ab}}{dz} = k_{1} 〈 C_{A} 〉 & (14.50) \end{matrix}

$\begin{matrix} - 〈 υ 〉 \frac{d C_{Ab}}{dz} = k_{1} 〈 C_{A} 〉 & (14.50) \end{matrix}$

Integrate both sides from 0 to L for z and show that a macroscopic model is obtained. State the definition of the rate term to be used in this (macro) model.

14.5 Dispersion coefficient from tracer data. Levenspiel and Smith (1957) injected a pulse of KMnO₄ into a tubular reactor 2.72 m long with a flow velocity of 35.7 cm/s. The tracer concentration measured at the exit was as follows:

Time	0	2	4	6	8	10	12	14	16	18	20
Concentration	0	11	53	64	58	48	39	29	22	16	11

Time	22	24	26	28	30	32	34	36	38	40
Concentration	9	7	5	4	2	2	2	1	1	1

Evaluate the moments of the above tracer data. From the second moment calculate the dispersion coefficient in the system.

14.6 Dispersion model for laminar flow reactor. Evaluate the performance of a laminar flow reactor using the dispersion model for the following conditions: first-order reaction with a rate constant of 0.1 s^–1, L = 100 cm, tube diameter = 1 cm, flow velocity = 0.2 cm/sec, and diffusivity = 2 × 10^–9 m²/s.

14.7 Dispersion model for turbulent flow reactor. Evaluate the performance of a reactor in turbulent flow and compare it with a plug flow reactor for the following conditions: first-order reaction with a rate constant of 5s^–1, L = 100 cm, tube diameter = 1 cm, flow velocity = 10 cm/sec, diffusivity = 2 × 10^–9 m²/s.

14.8 Mesoscopic model for a heterogeneous reaction. Consider a case where there is no homogeneous reaction and species A diffuses to the wall and undergoes a heterogeneous reaction. State the convection-diffusion model together with the appropriate boundary conditions. Determine a cross-sectional average of this model to provide a mesoscopic model for the system. State the closure relations needed for this case. Extend the analysis where both homogeneous and heterogeneous reactions of species A are taking place.

14.9 Numerical solution of the transient dispersion model. Determine the time domain solution for the transient dispersion model (Equation 14.11) using PDEPE. Note that the right-hand side of Equation 14.11 is to be rearranged to the derivative of a (combined) flux term. You may also want to compare your numerical solution with the analytical results shown in Equation 14.18.

14.10 Laplace domain response. Show all steps leading to Equation 14.15 and derive this equation. State the formula to find the moments of the response directly from the Laplace domain. Verify that the first moment is one and that the variance is given by Equation 14.17.

14.11 Laplace domain response for an open-open system. Consider the open-open case discussed in the text. State the proper boundary conditions to be used in this situation. Derive an expression for the response at z = L in the Laplace domain: find the moments of the response and verify the results shown in the text.

14.12 Time domain response for an open-open system. Find the time domain solution for the open-open system and verify the following result by Levenspiel and Smith (1957):

{〈 c 〉}_{e} = \frac{1}{2 \sqrt{π t * / P e *}} exp [\frac{- (1 - t *)^{2}}{4 t * / P e *}]

${〈 c 〉}_{e} = \frac{1}{2 \sqrt{π t * / P e *}} exp [\frac{- (1 - t *)^{2}}{4 t * / P e *}]$

14.13 Comparison with ideal reactors. A first-order reaction is taking place in a reactor 2 m long with a rate constant of 2 s^–1. The flow velocity is 5 cm/sec. A tracer experiment was performed and the variance was obtained as 40 sec². Find the following: dispersion coefficient in the reactor; the corresponding exit conversion; the conversion if the reactor were modeled as plug flow; the conversion if the reactor were modeled as a backmixed flow; the number of tanks that can be used to represent the system; the conversion based on the tanks in series model.

14.14 Comparison of the mixing cell and the dispersion model. Tracer experiments for a reactor showed that the dimensionless variance is equal to 4. A first-order reaction is taking place in this reactor with the Da parameter equal to two. If you were to model this by the dispersion model, determine the value of the dispersion Peclet number to be used. Find the conversion in the reactor. If the same reactor is to modeled by the tanks in series model, determine the number of tanks needed to provide the same exit age distribution. Find the conversion in the reactor based on the tanks in series model.

14.15 Taylor dispersion in non-Newtonian flow. The following equation can be derived for the velocity profile for a power law fluid under laminar flow conditions:

υ_{z} = \frac{3 n + 1}{n + 1} 〈 υ 〉 (1 - ξ^{2})

$υ_{z} = \frac{3 n + 1}{n + 1} 〈 υ 〉 (1 - ξ^{2})$

with n being the power law index. Follow the approach given in Section 14.3 and derive an expression for the Taylor dispersion coefficient for a power law fluid.

14.16 Taylor dispersion in channel flow. The following equation can be derived for the velocity profile for a Newtonian law fluid under laminar flow conditions:

υ_{x} = \frac{3}{2} 〈 υ 〉 (1 - ξ^{2})

$υ_{x} = \frac{3}{2} 〈 υ 〉 (1 - ξ^{2})$

Here ξ is the dimensionless distance starting from the center of the channel. This is defined as y/H with H being half the channel width. Follow the approach given in Section 14.3 and derive an expression for the Taylor dispersion coefficient for channel flow given in the text.

14.17 Dispersion coefficient in packed bed. A packed bed contains 3 mm particled in a 2 cm diameter tube that is 1 m long. The bed porosity is estimated as 0.6. Find the dispersion coefficient for a superficial liquid velocity of 5 cm/s. Properties of the fluid may be assumed to be the same as water.

14.18 Murphree efficiency for tray columns. An application of the plug-backmixed model shown in Section 14.7.1 is to find the vapor tray efficiency in a distillation column. The schematic of this is based on Figure 14.9. Here a vapor is bubbling through a pool of liquid and the vapor flow is assumed to be in plug flow. The liquid on the tray is assumed to be well mixed. The Murphree vapor efficiency is defined as

Diagrammatic illustration of Murphree efficiency for tray columns.

Figure 14.9 Schematic of a distillation tray for derivation of the Murphee vapor efficiency, from Seader et al. (2011).

E_{MV} = \frac{y_{A, in} - y_{A, out}}{y_{A, in} - y_{A *}}

$E_{MV} = \frac{y_{A, in} - y_{A, out}}{y_{A, in} - y_{A *}}$

where y_A is the vapor composition if the vapor were to achieve equilibrium with the exit liquid. Show that this can be expressed as

E_{MV} = \frac{1 - c_{AG, e}}{1 - c_{A L *, e}}

$E_{MV} = \frac{1 - c_{AG, e}}{1 - c_{A L *, e}}$

in terms of the variables shown in Section 14.7.1.

Show that the Murphree efficiency in a tray column is equal to ε directly by using Equation 14.35.

The assumption of a liquid being backmixed is suitable for small-diameter columns. Corrections to account for the deviation of the liquid flow from complete backmixing have been also proposed in the distillation literature.

14.19 A model for a fluid bed reactor. A fluid bed reactor is modeled assuming that the bed consists of two phases: a bubble phase in plug flow and an emulsion phase in backmixed flow. Reaction takes place only in the emulsion phase since this is where most of the catalyst is present. Develop a model along the lines of the plug-backmixed two-phase flow shown in the text. You need to add a reaction term to the liquid (in this case the emulsion) balance. Find the exit conversion. Show that this can be lower than that in a CSTR. A schematic of the model is shown in Figure 14.10.

Figure shows two diagrams, one showing the schematic of a fluid bed reactor, while the other showing the reactor as two-phase backmixed system.

Schematic diagram: A cylindrical column is shown to have "Gas in" inlet at the bottom and "Gas out" outlet at the top. The column is shown to contain fluid, along with bubbles and emulsions. The bubbles are denoted as gas pockets rising at high velocity resembling cloud-like fragments. The emulsions are denoted as gas plus catalyst resembling small spots scattered. Model: The cylindrical column is divided into two vertical columns with a dotted, vertical line. The left segment has "Bubble phase - plug flow" and the right segment has "Emulsion phase - backmixed." The Gas in, u subscript G, is split into two and fed in separately to the two phases. The bubble phase gets "u subscript G minus u subscript mf" while the emulsion phase gets "u subscript mf." The mass exchange is shown to happen from bubble phase to emulsion phase. The two phases are shown to have separate outlets, which are combined and sent out as "Gas out."

Figure 14.10 Schematic of a fluid bed reactor and its model representation as a two-phase plug-backmixed system.

14.20 Breakthrough time in an adsorption column. An adsorption column is operating at a gas superficial velocity of 30 cm/s in a packed bed with a bed porosity of 0.5. The adsorption equilibrium constant is 5000. If a step tracer of an adsorbing gas is introduced into the system inlet, at what time will the tracer start to appear at the exit? Assume plug flow.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Chapter 14. Mesoscopic Models and the Concept of Dispersion

Create new playlist

Sign In

Sign Up

Chapter 14. Mesoscopic Models and the Concept of Dispersion

14.1 Plug Flow Idealization

14.2 Dispersion Model

Dimensionless Parameters

14.2.1 Boundary Conditions

14.2.2 Solution for a First-Order Reaction

14.2.3 Nonlinear Reactions

14.2.4 Dispersion Model: Numerical Code Using CHEBFUN

14.2.5 Criteria for Negligible Dispersion

14.3 Dispersion Coefficient: Tracer Response Method

14.3.1 Laplace Domain Solution

14.3.2 Moments of the Response Curve

Open-Open Boundary Conditions

14.3.3 Time Domain Solution

14.4 Taylor Model for Dispersion in Laminar Flow

14.5 Segregated Flow Model

14.6 Dispersion Coefficient Values for Some Common Cases

14.7 Two-Phase Flow: Models Based on Ideal Flow Patterns

14.7.1 Plug-Backmixed Model

14.7.2 Non-Idealities in Two-Phase Flow

Concurrent Flow

Countercurrent Flow

Tanks in Series Model

14.8 Tracer Response in Two-Phase Systems

14.8.1 Single Flowing Phase

Effect of Internal Diffusion

14.8.2 Two Flowing Phases

Summary

Review Questions

Problems

Table of Contents for
Chapter 14. Mesoscopic Models and the Concept of Dispersion