Chapter 23. Biomedical Applications

Mass transfer principles find important applications in biomedical engineering. For a biomedical engineer a mechanistic understanding of processes such as oxygen transport in lungs and tissues is important per se and also in evaluating medical conditions and adjusting the treatment protocols. For pharmacokinetic scientists who deal with the study of distribution of a drug and its metabolism in the body, the modeling of mass exchange between various compartments/organs is the main tool needed. For the design of many extra-corporal devices, for example, dialysis, membrane oxygenators, artificial liver, and so on, it is necessary to evaluate the role of transport in the equipment and adjust the operating conditions accordingly. Hence we note that modeling of these systems where mass transport plays a key role is an important component of biomedical engineering. The goal of this chapter is to take some of these examples, illustrate how fundamental transport considerations are useful to model, and analyze these processes.

The analysis presented in this chapter is at a simplified level, making some assumptions but nevertheless providing important information and indicating the main factors affecting the process. Upon studying this chapter you will be able to see how the concepts learned in Part I of the book can be applied to prototypical biomedical problems. This broadens your skill in applying mass transfer principles to a wider class of problems than in traditional chemical engineering.

Transport of gaseous species (in dissolved form) is encountered in a number of organs and is shown schematically in Figure 23.1. Two main mass transfer steps are oxygen exchange in lung to blood and oxygen transfer from blood to tissues. Mass transfer–based models to describe these are discussed in Sections 23.1 and 23.2 respectively. Analysis of distribution of drugs together with their metabolism can be modeled by the compartmental models that were introduced in Section 13.8. Additional information and some more detailed modeling trends are then shown in Section 23.3. Modeling of extracorporal devices is illustrated by a mesoscopic-based model for a hemodialyzer in Section 23.4. Here we also show how this model can be linked to a compartment model to simulate the patient blood concentration during a dialysis treatment.

O₂ + Hb ⇄ O₂Hb

Using the law of mass action, we obtain

K=[O2Hb][Hb][O2]

where the square bracket shows the concentration. K is the equilibrium constant for the reaction.

Using Henry’s law [O₂] = p_O2/H_O2. Let S be the fraction of Hb existing in oxygenated form. Then [O₂Hb] = C_T S and [Hb] = (1 – S)C_T where C_T is the total concentration of Hb in oxygenated plus free form. Using these in the law of mass action, we have

KpO2HO2=S(1−S)

Solving for S, we get

The above model based on a single reaction scheme does not fit the actual data, which shows an S-shaped curve as shown in Figure 23.2. This is ascribed to oxygen binding to more than one site in a cooperative manner. There are four heme groups in Hb. Binding of oxygen to the first heme group facilitates binding to subsequent sites, resulting in the S-shaped curve shown in Figure 23.2.

The equilibrium curve is therefore fitted as

This is referred to as Hill’s equation. The equation is often written as

Here p₅₀ is the partial pressure at which the oxygen saturation is 50%.

The exponent should be four if oxygen binds consecutively to the four sites. The data, however, fits with an exponent of 2.7. The value of p₅₀ is 26 mm Hg.

For oxygen binding to myoglobin (a carrier found in muscles) the single site saturation curve given by Equation 23.1 fits the data well. Hill’s model with n = 1 and p₅₀ = 5.3 mm Hg is used for this case.

The opposite happens in the lungs where CO₂ is transferred to air. The accompanying decrease in CO₂ causes a shift to the left and increases saturation capacity for oxygen in blood. Thus nature has fine-tuned the equilibrium to accommodate both absorption and desorption!

1. Transport across the alveolar gas phase

2. Transport across the alveolar epithelium and capillary endothelium

3. Diffusion and convection in the blood plasma

4. Diffusion across the red cell membrane

5. Diffusion with reaction in red blood cells (RBCs)

Each step except the last is in series and can be modeled using a transport coefficient. The last step (diffusion and reaction in parallel) can be modeled using the concepts borrowed from gas–solid catalytic reactions using an effectiveness factor. The contribution to the total resistance for each of the four steps occurring in series is shown next. An overall transport coefficient is calculated for steps 1 to 4 and incorporated into the diffusion-reaction model for RBCs (red blood cells) by defining an overall effectiveness factor. The rate of uptake of oxygen can then be calculated.

1. Resistance due to diffusion in the gas phase is usually small and can be neglected due to the order of magnitude difference in the diffusivity in the gas phase compared in the liquid phase. This step is therefore not included in further analysis.

2. Diffusion across the alveolor membrane and the endothelium can be described by a permeability P_M. This is equal to the diffusion coefficient divided by the thickness of the membrane. A value of 0.387 cm/s for P_M is indicated by Truskey et al. (2004).

3. The transport coefficient in plasma, k_P , should be based on a convection-diffusion model. The Sherwood number is used as the measure of the transfer coefficient. This is defined as k_pL/D, where L is the thickness of the plasma layer, which is on the order of 0.35 μm to 1.5 μm. D is the diffusion coefficient of oxygen in plasma, which has a value of 2.4 × 10^–5 cm²/s. Based on the literature data, Truskey et al. (2004) suggest a value of 1.468 for the Sherwood number. Hence the mass transfer coefficient in the plasma is estimated as 0.44 cm/s.

4. Red cell membrane (endothelium) is about 10 nm thick. The solubility of oxygen is also about double that in plasma. Consequently the permeability of this membrane is about 48 cm/s. This value is much larger than the values for step 2 and 3. This resistance due to this transport can therefore be neglected.

From this discussion, we find steps 2 and 3 offer the main resistances for oxygen to reach the red blood cells from the alveolar gas space. These steps occur in series and can be combined into a single overall transfer coefficient, P_T:

Transport in red blood cells with reaction can be characterized using an overall effectiveness factor. If RBC (red blood cell) is treated as an equivalent slab with a characteristic length parameter of L_RBC and a first-order uptake reaction with oxygen can be assumed, then the effectiveness factor is given by Equation 18.8 in Chapter 18:

The two parameters required in the preceding equation are as follows.

First is the Thiele modulus, defined as

ϕ=LRBCkDRBC

This is in the range of 0.6 to 2.2 and hence there is some drop of oxygen concentration in the interior of the red blood cell.

The second is the Biot number, defined as

Bi=PTLRBCDRBC

where P_T is defined in Equation 23.4. The Biot number, in turn, can be shown to be in the range of 5 and hence the “external” mass transfer contributes to some extent as well (about 20% of the overall resistance).

The rate of oxygen uptake is then calculated as

Rate per unit volume of RBC = k₁ η(C*_A – C_A)

where C*_A is the saturation solubility of oxygen in blood, which is equal to p_O2/H_O2, H_O2 being the solubility coefficient. C_A is the total oxygen concentration in the RBC.

The rate of transport per unit volume of the capillary is then obtained by multiplying this by the hematocrit value (ratio of volume of RBC to volume of capillary), denoted as f_HB here:

Rate per unit volume of capillary = f_HBk₁η(C*_A – C_A)

The rate provides the local model, which can then be used in an overall balance model for the entire length of the capillary. This is addressed next.

The total concentration of oxygen (in plasma and bound to RBCs) in the capillary is treated as a variable. Note that this is a cup-mixed radial average concentration. The mass balance for oxygen is

In – out + transferred across the alveolus = 0

In mathematical terms:

Here v is the velocity of blood flow in the capillary. This leads to the following differential equation for the variation of the oxygen concentration along the length of the capillary:

The solution to this differential equation with the inlet condition of C_Ai at z = 0 provides the expected exponential profile for oxygen concentration along the length of the capillary:

CA=CAiexp(−fHBk1ηυz)+CA*[1−exp(−fHBk1ηυz)]

The group υ/[f_HBk₁η] has units of length and can be viewed as the characteristic distance for oxygen uptake. Over 99% of the saturation can be expected for a distance equal to five times the characteristic distance. The order of value of the characteristic distance can be shown to be 40 μm. Thus saturation occurs in a distance of 200 μm or so, which is much smaller than the length for mass transfer, which can be approximated as the circumference of an alvelous (754 μm). Hence the lung is an overdesigned piece of equipment with a size more than double that required for saturation.

In this model, each capillary is assumed to be cylindrical with a radius R_C. A tissue region of radius R₀ is associated with each capillary. This radius R₀ is taken as the half-distance between the center of two capillaries. Note from the figure that the model fails to account for some tissue areas near R₀. But the assumption is needed so that a simple unit cell concept can be used to simulate the problem. In practice the effect of this small region is expected to be minor. Also note that the model is not applicable to a complex arrangement of capillaries such as in brain tissue.

The Krogh model assumes that there is a zero-order consumption of oxygen in the tissues leading to

The boundary conditions are saturation oxygen concentration in blood of C_As at r = R_C and no flux of oxygen conditions at r = R₀.

The dimensionless representation is achieved by defining the following reference scales: reference length = R₀; reference concentration = C_As the concentration in the blood. The corresponding dimensional variables are as follows: the distance ξ is defined as r/R₀ and the concentration c_A is defined as C_A/C_AS. Then the parametric representation of the problem can be shown to be

cA=cA(ξ;ϕ02, κ)

Here ϕ02 is the Theile modulus for a zero-order reaction, defined as

κ is the ratio R_C/R₀.

A solution can be obtained analytically for the concentration profile. The critical value of the parameter ϕ02 at which the oxygen concentration drops to zero at r = R₀ is obtained as

For φ₀ values larger than this, there is a region of zero oxygen concentration referred to as an anoxic region at the end region of the tissue (near R₀). If such a region persists for long time, a part of the tissue will die, leading to a condition known as necrosis. Although necrotic conditions are rare in normal conditions, they can arise in tumors due to a higher rate of metabolism (higher k₀ values for tumor cells).

Some limitations to the Krugh model are now briefly indicated:

• The unit-cell model assumes close-packed tissue and excludes about 21% of the tissue. It therefore underestimates oxygen consumption. Other unit-cell models are considered in later studies, such as hexagonal arrangement of capillaries, but any such arrangement other than the cylinder requires a numerical solution.

• The model does not assume the discrete nature of the red cells and oxygen is assumed to be released uniformly in the plasma.

• The role of myoglobin, which binds with oxygen in the tissue, is not explicitly accounted for.

Details of modeling these issues are not considered here and interested students may wish to see the references cited by Truskey et al. (2004) in this area.

In – out – transferred to the tissues = 0

The differential equation for this is then

where C_A is the oxygen concentration in the capillary and η is the effectiveness factor for the tissue. η is equal to 1 as long as the Thiele parameter is less than the critical value at all points along the length of the capillary.

A rather interesting consequence of zero-order behavior is observed here. The concentration C_A decreases linearly along a length until a critical length, L*, is reached. This critical length corresponds to a position along the capillary where the outer corner of the tissue becomes anoxic. that, the length at which ϕ₀ becomes equal to ϕ₀ critical given by Equation 23.10. The effectiveness factor in Equation 23.11 is taken as one until this point.

For further increase in length, an anoxic core (called the lethal corner) develops near the outer radius of the tissues (see Figure 23.5). The behavior in this region is more like a half-order reaction with respect to oxygen concentration. The effectiveness factor has to be calculated as the region of the total tissue volume minus the anoxic region volume for L > L* and is used in the integration of Equation 23.11 for lengths greater than L*. These complexities are not addressed here but you should be in a position to model these following the zero-order reaction discussions in Chapter 18.

If one ignores this complexity and assumes a zero-order metabolism throughout the tissue, then the following expression is obtained for the length at which the oxygen concentration becomes zero:

This provides an approximate estimate of the length at which the oxygen concentration drops to zero.

We now switch gears to study models for drug metabolism in the body.

The second level of approximation is the two-compartment model shown in Figure 1.15 and simulated by a worked problem in Example 12.2. It can be shown that the one-compartment model can be obtained from this model by adding the two equations in the two-compartment model and then assuming that the exchange coefficient is rather large. Drugs that are lipid soluble often exhibit such behavior. These are often referred to as flow limited or perfusion limited since the drug concentration is determined by the flow at which it is injected and the metabolic rate for drugs that are lipid insoluble the exchange is often limited by the permeability of the capillary membrane, which is referred to as diffusion-limited behavior. It is useful to know these two limiting cases.

The third level of modeling is the physiologically based compartments model, which is discussed at the end of this section.

The compartments are assumed to be well mixed. The assumption that the blood compartment is well mixed may be puzzling to some readers. One has to compare the blood circulation time to the half-life time of a drug in the body. The cardiac output rate is about 5 L/min and the blood volume is 4 L and hence the circulation time is about 48 sec. A typical time for a drug to metabolize is on the order of hours and assuming that the blood compartment is well mixed is therefore a reasonable assumption.

−RA=kEOCAKM+CA

Here k is the rate constant, K_M is the Michaelis constant, and E₀ is the total concentration of the enzyme. E₀ is total enzyme concentration and C_A is the drug concentration.

The Michaelis-Menten kinetics reduces to a first-order equation for low concentration of the drug, that is, when C_A << K_M. In that case

–RA=kEOKMCA=k1CA

This explains the use of the first-order kinetic model in many studies. The first-order kinetics also permits the use of powerful matrix-based solution methods for the system of differential equations. Hence a larger number of compartments can be used in the model without adding significantly to the computational efforts.

Number of compartments to be used depends on the organs where the drug accumulation and metabolism is significant. In other words, organs where the drug concentration is expected to be low are omitted in the model in order to keep the model manageable. Further improvement is that each organ is divided into three subcompartments as illustrated in Figure 23.6.

The subcompartments used are the vascular region, which is the plasma perfusing the organ, the interstitial space, and the cellular space. Mass exchange is assumed between the vacular and the interstitial space as well as between the interstitial and the cellular space. A reaction is assumed to take place in all the three subcompartments. Thus three differential equations are set up for each organ included in the model. Further details are not presented here. An illustrative study on methotrexate, a cancer drug, has been presented by Bischoff et al. (1971) and this topic is also discussed by Truskey et al. (2004).

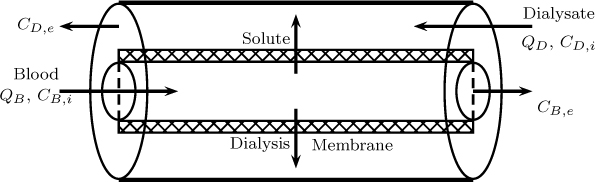
The schematic of the dialyzer is shown in Figure 23.7 where the blood stream is flowing countercurrent to a dialysate stream. A hollow fiber arrangement is shown in Figure 23.7.

A mesoscopic model is illustrated here. Since the flow in the blood side is usually under laminar considerations, dispersion effects are added in the model. The dialysate side is modeled using plug flow. Model equations based on these flow pattern assumptions are shown next.

where M˙bd is the transfer rate of the solute from the blood side to the dialysate side per unit perimeter and v_B is the blood flow velocity. s is a shape parameter equal to zero for channel flow with R being half the width of the channel, while s is equal to one for a hollow fiber circular channel with R being the radius of the fiber.

The mass balance on the dialysate side is based on the plug flow and leads to

where Q_D and Q_B are the volumetric flow rate of the dialysate and blood, respectively. C_D is the concentration of the solute in the dialysate side.

The transfer rate is modeled using resistances in series. The transfer involves three steps in series with each step offering its own resistance:

1. Transfer from the bulk of the blood stream to the inner surface of the membrane. This can be modeled using a mass transfer coefficient k_L with 1/k_L being the resistance.

2. Transfer across the membrane to the dialysate side. This can be modeled using a membrane permeance P_M with 1/P_M being the resistance.

3. Transfer from the walls of the membrane on the dialysate side to the bulk dialysate stream. This can be modeled using a mass transfer coefficient k_D with 1/k_D being the resistance.

The overall resistance ∑R is the sum of these three resistances:

∑R=1kL+1PM+1kD

Hence the transfer rate is given by

M˙bd=(CB−CD)∑R

This completes the model formulation. The Danckwerts boundary conditions are used for the blood side since the dispersion model is used here while the inlet concentration of the solute is used at the inlet side of the dialysate. The model can be solved analytically after suitably combining Equations 23.13 and 23.14. Some details of how to proceed are indicated in exercise problem 23.13 and also in Ramachandran and Mashelkar (1980). The theoretical predictions for the parallel plate hemodialyzer were checked with the experimental data of Grimsrud and Babb (1966) and the data of Ramirez et al. (1971) and a close fit was observed. The sensitivity of model parameters were also investigated. In particular the diffusion coefficient of urea in blood is shear rate dependent (Hyman, 1975) due to the non-Newtonian nature of the blood. Hence sensitivity studies of model parameters are important in general. In this particular case, the sensitivity to variations in diffusivity of the solute was found to be less than 20%.

The mesoscopic model for the dialyzer shown earlier provides the clearance rate of the plasma compartment, which is equal to Q_B(C_B,i – C_B,e). The sensitivity to the exchange parameter was also demonstrated. Once calibrated, the model is useful to formulate a treatment protocol to control the concentration of urea in both the blood stream and in the tissue compartment.

One interesting factor was that the rate of removal has to be restricted so that significant differences in concentration in the two compartments do not develop. This can be achieved by decreasing the dialysate flow rate, increasing the solute concentration in the dialysate, or increasing the blood flow. Detailed results are not presented in the interest of brevity; please refer to Ramachandran and Mashelkar (1980) for the various parametric plots.

23.2 How does the carbon dioxide concentration in Hb affect oxygen dissociation?

23.3 What causes carbon monoxide poisoning?

23.4 What are the limiting transport steps in oxygen absorption in the lungs?

23.5 Explain how the effectiveness factor concept is useful to calculate the local rate of absorption of oxygen in lungs.

23.6 Define the characteristic distance for oxygen uptake and its meaning.

23.7 What is the physical picture upon which the Krogh cylinder model for oxygen transport in tissue is based?

23.8 When can an anoxic region develop in the tissue?

23.9 What is the lethal corner and what is the cause of it?

23.10 Justify the assumption that the blood (plasma) compartment is well mixed although it is in circulation inside blood vessels.

23.11 For pharmacokinetic modeling, when is a one-compartment model suitable and when it is not?

23.12 What is the PBPK model?

23.13 Show the similarity in the hemodialyzer modeling and modeling of a conventional chemical engineering separation process.

23.14 Discuss briefly how the patient-dialyzer linked model is useful in clinical applications.

L + nA ⇄ AL_n

The notation A is used for oxygen and L is used for Hb (the ligand). Apply the law of mass action to this scheme and show that

[AL_n] = K[A]ⁿ[L]

where the square bracket represents concentration. The total balance for the ligand requires n[AL_n] + [L] = [L_T] with L_T being the total ligand concentration. Combine the two equations and shown that Hill’s equation results for oxygen saturation.

23.2 Total oxygen concentration in blood. Hematocrit refers to the volume fraction of RBCs in blood and is on the order of 0.45. Find the oxygen concentration in plasma using Henry’s law. Find the concentration of oxygen bound to RBCs using Hill’s equation. Find the total concentration of oxygen if the atmospheric pressure is 760 mm Hg at a sea level locations and 670 mm at a higher elevation of 1 mile.

The solubility coefficient of oxygen in plasma is equal to 1.125 × 10^–11 mole/cm³Pa. Note that the oxygen mole fraction in the lung is less than 0.21 since the lungs are saturated with water vapor at 37°C. Please correct for this as well.

23.3 Oxygen saturation in anemia patients. People with anemia have lower Hb concentration. Determine the level of oxygen saturation if the Hb level is 0.1 g/mol compared to the normal level of 0.14.

23.4 Overall effectiveness factor for oxygen uptake. Calculate the effectiveness factor for the oxygen uptake in RBCs based on the following parametric values suggested by Truskey et al. (2004):

– Permeability of the capillary walls = 0.387 cm/s

– Mass transfer coefficient in plasma = = 0.44 cm/s

– Effective length of RBC = 1.35 μm

– Diffusion coefficient of oxygen in RBC = 6.0 × 10^–6 cm²/s

– Rate constant for first-order reaction ≈ 1000 s^–1.

23.5 Length needed for saturation. Calculate the characteristic parameter and the length needed for a capillary to be saturated with oxygen for the following conditions: blood flow velocity = 2.5 mm/sec; hematocrit value = 0.45. For other parameters use the values from the previous problem.

23.6 Application of Krogh model. Apply the Krogh model to the following data (from Truskey et al., 2004) to find the maximum intercapillary radius for no anoxic region formation. Metabolic rate = 1 × 10^–7 mol/cm³s, a zero-order reaction; capillary radius = 1.5 to 4 μm; D_O2 = 2 × 10^–5 cm²/s in tissue; oxygen concentration in blood at the given point: 4.05 × 10^–8 mol/cm³.

23.7 Oxygen variation with length in a capillary near tissue. Solve Equation 23.11 for C_A versus z for the data in the previous example. The velocity of blood is 2 mm/s. The inlet concentration of oxygen is 19.88 ×10^–3 M. Consider two cases. First, assume no anoxic region develops in the tissue. Find the length at which the oxygen concentration becomes zero. Second, assume an anoxic region forms and find the length at which the lethal corner can develop.

23.8 Model for NO distribution in blood and tissues. NO is a vasodilator and is produced in the endothelium of the blood vessel and the tissue epithelelium. NO then diffuses into the capillary as well as into the tissues, and also undergoes a reaction. A schematic of the process is illustrated in Figure 23.9.

The concentration profile of NO is important to assess the distance over which NO acts in the tissue. The NO concentration should remain above a critical value for it to be effective. The Krogh cylinder model is useful here. Assume the reaction is first order in NO. Show that the following equation is then applicable:

Show that this applies both to the capillary (0 to R_C) and the tissue (R_C to R₀). However, the equation needs to be solved separately for the two regions since the reaction rate is not the same in the two regions. The boundary condition at r = R_C also has to be matched for the two regions to get the complete solution. The boundary conditions at r = 0, the center of the capillary, and r = R₀ the outer edge of the tissue, are the no flux conditions. At r = R_C the concentration is continuous. Note that the thickness of the endothelium is ignored. The generation in the endothelium q˙NO provides the second matching condition at r = R_C. Show that the following condition holds at r = R_C:

q˙NO=DNO,BdCA,Bdr−DNO,TdCA,Tdr

Simulate and plot the NO profile in the blood and capillary for the following set of parametric values taken from Truskey et al. (2004):

– Production rate = 5.5 × 10^–12 mol/cm²s

– Rate constant for reaction in blood = 1000 s^–1

– Rate constant for reaction in tissue = 0.01 s^–1

– Diffusion coefficient in blood = 4.5 × 10^–5 cm²/s

– Diffusion coefficient in tissue = 3.3 × 10^–5 cm²/s

– Radius of the capillary - 25 μm

– Outer radius of the tissues = 100 μm

23.9 Nutrient limitation in tumor growth. Tumors pull nutrients needed for their growth from the surrounding tissues. If the tumor size becomes large, a region can develop inside the tissue where the nutrient concentration drops below a critical value. The growth is then limited by lack of nutrients. An illustrative concentration profile is shown in Figure 23.10.

Solve the model for a zero-order reaction in spherical coordinates. Develop an expression for the radius of the tumor at which the center concentration drops below a critical value. Note that the size of the tumor will be limited by this value because nutrient starvation occurs above this value. The model applies to the avascular stage of growth, that is, when the tumor has not developed its own blood vessels.

23.10 Tumor growth: inhibitor limited model. Tissues generate inhibitors, which are needed to control growth and other processes. Tumors also do this. Develop a diffusion-reaction model for a spherical shaped tumor that generates an inhibitor by a zero-order reaction and also destroys it by a first-order reaction. Solve for the concentration profile. An illustrative profile of the type shown in Figure 23.11 will be obtained.

The boundary condition at the edge of the tumor can be a Robin or Dirichlet type condition. The Dirichlet condition with zero concentration applies if the permeability of the tumor membrane is rather large. Set up and solve the model for both cases. The tumor growth will stop in regions where the concentration of the inhibitor is above a critical concentration (see Figure 23.11). Solve and plot the profiles for concentration for various radii and mark regions where the tumor ceases to grow, assuming a value for the critical concentration.

23.11 Solution for a three-compartment model. The plasma concentration of small molecules is best fitted by a three-compartment model. Truskey et al. (2004) suggests a central compartment where a drug is injected and cleared and two peripheral compartments as shown in Figure 23.12.

Set up the model and solve for the central compartment concentration as a function of time using the matrix method. Show that the concentration in the plasma (central compartment) can be represented as a triexponential solution of the following form:

C_p = C_p0 [ ₁ exp(– λ₁t) + α₂ exp(– λ₂t) + (1 – α₁ – α₂) exp(– λ₃t)]

Explain the relation of the constants α s and λ s to the volume parameters, clearance rate, and exchange rates.

23.12 Analytical solution to the dialyzer model. Equations 23.13 and 23.14 can be combined and the transfer rate term can be eliminated. The resulting equation can be integrated to get a relation between the dialysate concentration and the blood concentration. Show that the following equation results if this procedure is applied:

CD=CD,i+QBQD(CB−CB,e)−QBQDDEυBdCBdx

Now use this in Equation 23.13 to get a differential equation for C_B. This equation is very similar to the axial dispersion model; the only difference is that the coefficients are modified to include Q_B/Q_D ratio terms. The solution has the same form as the axial dispersion model and provides an analytical solution to the dialyzer model. Set up this equation and solve for the exit concentration of the solute in the blood stream.