Chapter 15. Mass Transfer: Multicomponent Systems

The goal of this chapter is to revisit the transport laws for multicomponent systems and to demonstrate tools by which multicomponent models are solved. In particular, the numerical solution of Stefan-Maxwell model is introduced and applied to many illustrative problems.

The set of problems examined is similar to those in Chapter 6 and later in 18 and show the multicomponent extension to these problems. First we show somewhat general code that couples and solves the Stefan-Maxwell model with the conservation equation. This code can be used for a variety of problems in both reacting and non-reacting systems. The use of this code for the analysis of diffusion with reaction in a porous catalyst is demonstrated and the results are presented for the concentration profile and the effectiveness factor for a four-component system with a simple reversible bimolecular reaction. This is an extension of the Fick’s law–based approach to such problems studied in Section 18.3.

The transport effects in a heterogeneous reaction at a catalytic surface are shown next. The film model is used, which is similar to that in Section 6.3 where the simpler concept of mass transfer coefficient was used. Here we demonstrate how the Stefan-Maxwell model can be used for transport in the film. A three-component system with a surface reaction is studied.

Examples of non-reacting systems are then discussed. The first example is evaporation of a volatile species in a gas mixture of two inert components, which makes it a ternary system. Analytical solutions can be derived for this case. We also demonstrate here that the Stefan-Maxwell equation can be approximated by the Wilke (1950) equation. Evaporation of two liquid components into an inert gas is studied next, followed by mass transfer in equimolar counterflow in a diffusion film; examples are shown where reverse diffusion and osmotic diffusion take place.

The last section introduces the concept of a generalized Fick’s law and the use of a matrix of diffusion coefficients to characterize a multicomponent system. The inverted form of the Stefan-Maxwell equation leads to the definition of a multicomponent diffusion matrix. The advantages and disadvantages of this approach are pointed out.

The velocity can be either with reference to a stationary frame or a moving frame since the difference of two velocity values rather than individual species velocity appears on the left-hand side of the above equation. The y is the mole fraction of the subscripted species.

The flux of A (in a stationary frame of reference) is related to the velocity of A by the relation N_A = Cy_Av_A; a similar relation for N_B holds as well. Equation 15.1 now reduces to the following equation with minor rearrangement:

This is the same as Fick’s law but the form is inverted; that is, the mole fraction of a species (A or B) is now given as a combination of the fluxes of the two species.

The following equation (in terms of the diffusive fluxes) holds as well since the velocity difference is the same with respect to a moving frame as well:

This is again an inverted form with the mole fraction term appearing explicitly.

where ns is the number of components and D_ij is the binary pair diffusivity for the i-j pair. The summation term is zero if j = A and is not needed.

Note that the equation can also be written in terms of the diffusive fluxes as

You should verify that both forms are equivalent. For problem-solving purposes, the form in terms of the combined flux (Equation 15.4) is more useful. The constitutive equations are supplemented with the species mass balance equations, which have the same form as in Section 5.1. Thus for a steady state case we have

The simultaneous solution to the two boxed equations, 15.4 and 15.6, will be our focus now and we shall present the application to illustrative multicomponent mass transfer problems.

Consider the reaction scheme taking place in a porous catalyst:

A + B ⇌ C + D

Let the rate model be given as

−R_A = k_f C_AC_B – k_bC_CC_D

This can be used in the conservation law (Equation 15.6) for species A to D. For example, using this for A we have

This generates four equations. Note that there is an invariance property due to the fact that the rate term is common to all four equations. Hence the fluxes are tied together by this invariant relation. (Hence there is only one independent value for the flux.) However, for numerical solution and for ease of code setup, we retain all four equations.

Additional equations arise by using the Stefan-Maxwell flux expressions (Equation 15.4) for each of the components. For example A we have

dyAdz=∑j=1nsyANj−yjNACDAj

Similar equations apply for species B, C, and D. Thus we have 2 * ns equations, eight for a four species system. Eight boundary conditions are to be specified at the two end points of the domain, 0 to L. These are problem specific and the examples provided illustrate how these may be specified. For example, if this reaction is taking place in a porous catalyst that is modeled as a slab of half-thickness L then the following boundary conditions can be applied:

• The flux is zero at x = 0 and hence N_A, N_B, and so on, are set as zero.

• The concentrations are specified at x = L and hence the mole fractions y_A and so on are specified.

Hence we generate eight boundary conditions by specifying either the flux or mole fractions.

The code in Listing 15.1 is somewhat general and useful for a variety of multicomponent diffusion problems with and without reaction. The main driver is shown first. The code uses CHEBFUN as a wrapper for the BVP4C code.

---

Listing 15.1 Program to Solve Multicomponent Diffusion with Simultaneous Chemical Reactions

Click here to view code image

global ns D Da K
ns = 4;
D =[  1.0000    0.7319    0.7188    0.7141
      0.7319    1.0000    0.2289    0.2138
      0.7188    0.2289    1.0000    0.1633
      0.7141    0.2138    0.1633    1.0000];
Da = 9; K = 5;
global db
db = D;
global ys
%% solver
length = 1. ; % dimensionless
ys = [ 0.33333 0.66667     0 0 ] % surface concentrations
d = [0,length];
one = chebfun(1,d);
eta = chebfun ( 'eta', d) ;
  % initial guess of rate
  rate = reactionrate (ys);
initguess = [ys(1)*one ys(2)*one ys(3)*one ys(4)*one ...
   rate*one rate*one –rate*one –rate*one];
%%%%%% call bvp4c now
sol = bvp4c (@odes, @bcs, initguess) % bvp solved
y = sol(:,1); % mole fraction of species one
plot(sol(:,1:2))
% effectiveness factor
rate_s = reactionrate (ys);
eta1 = sol(0,5)/rate_s % effectineess factor
%%%%

---

The dimensionless representation is used here with the distance being scaled by L. The flux is scaled as

NA*=NADrefC/L

A similar definition holds for B, C, and D. Here C (in the previous equation) is the total concentration in the bulk gas and D_ref is the diffusivity of a chosen species A. All other binary diffusivity is scaled by this value entered as a matrix D.

The set of functions to be solved is then specified in an m file denoted as odes here (Listing 15.2). The first four derivatives are for dy_i/dξ and the next four are for dNi*/dξ with i varying from 1 to 4 to cover the four components.

Listing 15.2 Code Defining the Differential Equations

Click here to view code image

---

%–––––––––––––––––––––––––––––––––––––––––––––––––––––––––
function dydx = odes ( x, y )
global dk db
global ns
rate = reactionrate(y);
   n1 = y(5); n2= y(6) ; n3= y(7); n4 = y(8);
   % na = y(3) ; nb= y(4) ; nc= –(na); y3= 1.–y(1) – y(2);
   bulkterm = zeros (ns,1);
   % species 1.
    T12 = y(2) * n1 /db(1,2) – y(1) * n2 /db(1,2) ;
    T13 = y(3) * n1 /db(1,3) – y(1) * n3 /db(1,3) ;
    T14 = y(4) * n1 /db(1,4) – y(1) * n4 /db(1,4) ;
    % species 2
    T21 = y(1) * n2 /db(2,1) – y(2) * n1 /db(2,1) ;
    T23 = y(3) * n2 /db(2,3) – y(2) * n3 /db(2,1) ;
    T24 = y(4) * n2 /db(2,4) – y(2) * n4 /db(2,4) ;
    % T2% species 3
    T31 = y(1) * n3 /db(3,1) – y(3) * n1 /db(3,1) ;
    T32 = y(2) * n3 /db(3,2) – y(3) * n2 /db(3,2) ;
    T34 = y(3) * n3 /db(3,4) – y(3) * n4 /db(3,4) ;
    % species 4
    T41 = y(1) * n4 /db(4,1) – y(4) * n1 /db(4,1) ;
    T42 = y(2) * n4 /db(4,2) – y(4) * n2 /db(4,2) ;
    T43 = y(3) * n4 /db(4,3) – y(4) * n3 /db(4,3) ;
    % dk is the Knudsen diffusion term.
    dydx = [– y(5) /dk(1)–T12–T13–T14
            – y(6)/dk(2)–T21–T23–T24
             –y(7)/dk(3)–T31–T32–T34
             –y(8)/dk(4)–T41–T42–T43
        –rate
        –rate
        rate
        rate ] ;

---

---

Listing 15.3 Code Defining the Boundary Conditions

Click here to view code image

function res = bcs ( ya , yb)
global ys
res = [ ya(5)
        ya(6)
        ya(7)
        ya(8)
        yb(1)– ys(1)
        yb(2)– ys(2)
        yb(3)– ys(3)
        yb(4)– ys(4) ] ;

---

The kinetic model to define the rate term is set as a separate subroutine to provide code flexibility. This will be zero for the non-reacting systems considered in Section 15.4. The code for simple bimolecular reverse reaction model is presented in the following:

Listing 15.4 Code Defining Simple Bimolecular Reverse Reaction Model

Click here to view code image

%–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
function ratemodel = reactionrate(y)
global ys
global ns D Da K
ratemodel = Da * (y(1)*y(2) – y(3)* y(4)/K)

---

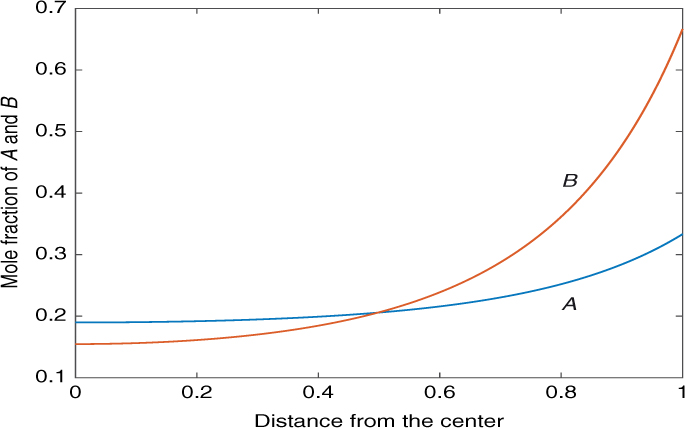
Illustrative results are shown in Figure 15.1. The dimensionless parameters are kf*=5 and K = k_f /k_b = 5. The bulk mole fractions are y_A = 1/3, y_B = 2/3. The effectiveness factor is calculated as 0.21. Species A is taken as the faster diffusing species here. We note that although the surface mole fraction of B is higher than A, the drop in concentration of B is much more than that of A, since B diffuses much slower than A.

It is fairly easy to modify and apply this code for multiple reactions. The rate of reaction can be calculated by using the stoichiometric matrix and a rate function for each reaction. Thus the rate of production for species i is given by the summation of its rate of production from all the reactions (subscript r) as

Ri=∑rnrνriRr

where nr is the number of reactions, ν_ri is the stoichiometry of the ith species in the rth reaction and Rr is the rate term for the rth reaction (which represents the molar rate of production of any species with unit stoichiometry). The rate term is now introduced into the species balance equations:

Equations 15.4, the constitutive model and Equation 15.8, the conservation model, have to be integrated together now. There are two equations for each species (one for the conservation law and the other for the constitutive model) and hence there are 2 * ns-first order differential equations to be solved simultaneously. These are boundary value types of problems.

Note that the number of equations can be simplified using the rank of the stoichiometric matrix; this is left as an exercise. For example, if there is a single reaction then there is only one independent flux, usually the flux based on a key component. The flux of all other species is determined simply by the stoichiometry of the reaction. Here we keep all 2 * ns equations for simplicity. This takes up slightly more computational time but keeps the implementation to new problems somewhat simpler.

For porous catalysts both Knudsen and bulk diffusion may be important. In such cases the contributions are added together and the Stefan-Maxwell model is modified as

Here D_Ke,i is the effective Knudsen diffusivity of i while D_ij,e is the effective binary pair gas phase difficulty (D corrected with the porosity and tortuosity factors).

The relative magnitude of the two terms in Equation 15.9 determines the nature of the solution method. If Knudsen dominates the fluxes are uncoupled while if the bulk gas diffusion dominates we expect multicomponent coupling effects, especially if the molecular weights of the diffusing species are vastly different. Uncoupled problems can be reduced to a set of second-order differential equations in concentrations and solved directly. Coupled problems are best solved by simultaneous computations of fluxes and concentrations by the code shown in Listing 15.1.

A → B + C

is taking place over a catalyst surface.

Then by stoichiometry the following conditions apply for the fluxes:

N_B = –N_A and N_C = –N_A

Thus N_B and N_C can be eliminated from the Stefan-Maxwell equations. In addition the mole fraction of one of the species, say, C, can also be eliminated using

y_C = 1 – y_A – y_B

The Stefan-Maxwell equation for A reduces to the following equation when these conditions are applied:

The equation for B becomes

The condition that no homogeneous reaction takes place provides the third equation:

Thus we track three variables simultaneously: y_A, y_B, and N_A. Three boundary conditions are needed to solve the problem. The gas composition in the bulk gas is specified, which provides two conditions. The additional condition to be imposed is based on the kinetics of the heterogeneous surface taking place at the surface and is discussed in the following.

• For fast reactions the Dirichlet condition is applied at the reacting surface. The mole fraction of A at the surface is now set as zero, which provides the third boundary condition. These equations can be used to solve for N_A and also for y_B,L, the mole fraction of B at the reacting surface.

• For a finite reaction case, the balance of flux of A at the reacting surface leads to the following boundary condition at the surface:

  N_A(z = L) = –R_A = k_sCy_As

  Note that the last term is specific for a first-order reaction at the catalyst surface. (z = L is the location of the reacting surface.) Thus a Robin type of boundary condition is now specified at the reaction surface.

This completes the problem specification; the system equations can be implemented in BVP4C and solved. Example 15.1 provides an illustration.

This, integrated across the system, provided an expression for the flux (Equation 6.18). In this section we extend the model to a ternary system with A evaporating into an inert gas mixture of B and C.

One approach is to use the pseudo-binary diffusivity for A, D_A–m, which can be calculated from the Wilke equation shown in Section 5.3. The expression for the flux then has a similar form as that for a binary:

Let us explore this in connection with the Stefan-Maxwell model first, where we show that for this specific problem it is an exact result that can be derived from the Stefan-Maxwell model. However, we will find that a unique value for D_A–m cannot be assigned immediately. A value based on some average composition has to be calculated and used.

Here we solve the Stefan-Maxwell model directly without having to use the pseudo-binary approach. First we demonstrate that the Wilke equation results from simplification of the Stefan-Maxwell equation.

If we have UMD then N_B and N_C are zero, which provides the determinacy condition. These are now used in the above equation, which simplifies to

Rearranging this we have the following expression for the flux:

The combined flux above is the sum of the diffusion and convection flux:

N_A = J_A + y_AN_t

For the system being studied, N_t = N_A. Also, expressing the diffusion in terms of a pseudo-binary diffusivity of A in the mixture, D_A–m, we have

Comparing this expression with that defined using the pseudo-binary diffusion coefficient (Equation 5.23 in Chapter 5), we find the pseudo-binary is defined according to the Wilke equation as

This is the basis for the Wilke equation. It therefore applies strictly speaking when only one species (A) is diffusing in a ternary mixture. The other two species have zero fluxes. Note that this is used as an approximation often even when these conditions do not hold. Hence the flux is given as

The advantage of this over the Stefan-Maxwell model is that it is flux explicit and similar to that for a binary case. The disadvantage is that D_A–m is mole fraction dependent (as can be seen from Equation 15.19) and hence varies along the diffusion or reaction path and has to be based on some representative mole fraction in the system. We do not know the mole fraction profiles a priori. The mole fractions are known in the bulk gas and can be used to find the pseudo-binary diffusivity as an approximation.

As an alternative we can track the concentration profiles for B and C, in other words solve the Stefan-Maxwell formulation directly. This approach is rather general and explored further in this section.

y_A = 1 – y_B – y_C

Also N_B = 0 and N_C = 0 (UMD).

With these substitutions the flux expressions for B and C are as follows:

dyBdz=NACDAByB

and

dyCdz=NACDACyC

Each equation can be integrated separately here since N_A is not a function of z. Note that this is not always true, for example, if a simultaneous homogeneous reaction of A is also taking place.

Integration with the boundary condition at z = L (the bulk gas) gives

y_B = y_BL exp[–N*(1 – z/L)]

and

y_C = y_CL exp[–N* (1 – z/L)]

where N* is a dimensionless flux defined as

N*=NA(CDAB/L)

and β is the diffusivity ratio defined as D_AB/D_AC.

Finally, applying the boundary condition at the surface, z = 0, (where the mole fraction of A is known by equilibrium considerations) we have

which provides an implicit equation for find N*.

We also note that the binary expression is recovered if β = 1, that is, when the binary diffusivity of A in B is the same as that for A in C, D_AB = D_AC. The effect of multicomponent interaction therefore depends on the β parameter.

Since C is inert we can set N_C = 0, which is the required determinacy condition. Also, since the mole fractions add up to unity, we have yC = 1 – yA – yB.

When these simplifications are introduced into the Stefan-Maxwell equations, we obtain the following equations for the mole fraction profiles of A and B:

and

The boundary conditions needed are as follows: at the evaporating surface, z = 0, the mole fractions are related to the vapor pressure values (assuming an ideal liquid), while at the bulk gas, z = L, the mole fractions are specified from the bulk gas values. Often a value of zero is used as a simplification.

The above differential equations are first order and look like initial value problems (IVPs); they are candidates for explicit marching in z or solvers such as ODE45. However, the fluxes are unknown and have to be computed by imposing the boundary condition at x = L. Hence this is a boundary value problem. We discuss two methods for solution of this problem. First is the direct use of BVP4C, which is similar to that discussed in Section 15.2. The second is based on matrix algebra, which is discussed next.

dydz=A˜y+R

where y is the solution vector; in the present case the solution vector has a dimension of two, representing yA and yB.

The term à above is the coefficient matrix and R is the non-homogeneous term. Since both the coefficient matrix and non-homogeneous term are constants, the solution can be represented in matrix form using the exponential matrix concept:

y = (y₀ + Ã^–1R)expm(Az) – Ã^–1R

where y₀ is the mole fraction at the evaporating surface.

Now using the conditions at the bulk gas the following algebraic relation is obtained:

This equation contains the unknowns N_A and N_B, which are buried in the à matrix. The solution of these “implicit” algebraic equations gives the fluxes. This can be accomplished, for instance, by using a nonlinear algebraic solver such as FSOLVE in MATLAB. Example 15.2 provides an illustration for evaporation rate in a binary mixture.

An example of equimolar counter-diffusion is found in the modeling of diffusion in a porous plug separating two regions of different gas compositions. The binary case was examined in Example 5.2 and exercise problem 4 in Chapter 6. The compositions at the two ends are specified and the fluxes of the various species are to computed. The determinacy condition used here is that there is equimolar counter-diffusion.

A second example is in distillation of a ternary mixture. Since distillation is usually under adiabatic conditions, we assume equimolar diffusion. This assumes that the molar heat of vaporization of the three species is nearly equal. Then the total flux across the system is zero in order to maintain the heat balance and the problem reduces to equimolaar counter-diffusion.

The Stefan-Maxwell model is simplified by using the following conditions. The total flux is zero, which provides the determinancy N_t = 0, or

N_C = –N_A – N_B

The second simplification to be used in the Stefan-Maxwell model is that mole fractions have to add up to unity and hence

y_C = 1 – y_A – y_B

The mole fraction y_C and flux N_C are then eliminated from the Stefan-Maxwell equations for both dy_A/dz and dy_B/dz. The resulting equations can be solved by the matrix method (followed by FSOLVE) or by the BVP4C routine. Example 15.3 shows an application to the flux calculation in the distillation of ternary mixture.

An inverted formulation of the Stefan-Maxwell model leads to a generalized Fick’s law for diffusion fluxes. The form of the equation is similar to a binary mixture and is the vector analog of the law. A matrix is introduced for the diffusivities in this model.

We consider a ternary system for simplicity. Extension to quaternary systems and so on is straightforward but lengthy.

The idea is to write the diffusion flux explicitly. Since the diffusion flux of species A (denoted as 1 here) may depend on the mole fraction gradient of both A (1) and B (2), it is written as

J1−CD11∇y1−CD12∇y2

Here D is used as the coefficient matrix and is a measure of the diffusion coefficients. Note that these are not binary pair diffusion coefficients and the relation between the two will be shown soon. Hence the symbol D˜ is used for this matrix. Note that ∇y₃ is not independent and therefore not used in the flux expression.

A similar equation is written for species 2:

J2−CD21∇y1−CD22∇y2

Thus we use four constants to model the diffusion. These four constants can be put into a matrix, which is called the generalized Fick’s law diffusion matrix. Also note that the equation for species 3 is redundant since the diffusion fluxes have to add up to zero.

Note: Although four values for D˜ are needed for a ternary case (and (ns – 1)² in general for a ns component system), there are some restraints between these values, which reduces it to three independent values or ns(ns – 1)/2 in general. These are shown by De Groot and Mazur (1968). The restraint arises from what are known as Onsager reciprocal relations. But in practice these restraints are difficult or even impossible in most cases to apply and the four for binary or (ns – 1)² values in general are commonly used.

The Stefan-Maxwell model in diffusion flux form (Equation 15.5) is used here, and is repeated for ease of reading:

A similar equation holds for species 2. We take ns = 3 here, that is, a ternary system.

Two substitutions are made here: (1) J₃ = –(J₁ + J₂) since the diffusion fluxes have to add up to zero and (2) y₃ = 1 – (y₁ + y₂), as the summation of mole fractions should be one.

This permits the flux and the mole fraction of the species to be eliminated from the Stefan-Maxwell equation. The eliminated species is sometimes called the solvent. The resulting equation after some simple algebra is

where ns represents the species that was eliminated, species 3 for the ternary case considered above. The summation is not applied if i equals j.

Equation 15.26 can be represented in compact vector-matrix form as

Here B˜ is a 2 by 2 coefficient matrix for a ternary system. This matrix is obtained by gathering all the coefficients of J_i on the right-hand side of Equation 15.26.

The matrix representation can be inverted to obtain J in terms of the mole fraction gradients and the resulting equation can be represented as

where D˜ is equal to

D˜=[B˜]−1

Equation 15.28 defines the diffusivity matrix D˜ and has a form similar to Fick’s law except that it is now in a vector matrix form. The matrix D˜ is the tensor equivalent to the binary diffusivity. The form above is often referred to as the generalized Fick’s law.

The explicit form for the D˜ matrix can be obtained for a ternary system analytically and are presented in Table 15.1.

Table 15.1 Explicit Expressions for the D˜ Matrix for a Ternary System

D11=[y1D12+y2+y3D23]/DENO

D12=[y1(1D12−1D13)]/DENO

D21=[y2(1D12−1D23)]/DENO

D22=[y2D12+y1+y2D13]/DENO

DENO=y1D12D13+y2D12D23+y3D13D23

An often quoted and well studied problem is the hydrogen(1)-methane(2)-argon(3) system and we calculate the values of D˜ for this case from the equation shown previously for a composition of y₁ = 0.2, y₂ = 0.2, and y₃ = 0.6; the results are as follows:

D₁₁ = 0.76 × 10^–4 m²/s

D₂₁ = –0.01 × 10^–4 m²/s

D₂₁ = –0.12 × 10^–4 m²/s

D₂₂ = 0.25 × 10^–4 m²/s

Note the reasonably large value for the cross-diagonal term D₂₁. Complex diffusion effects are signaled by this term. Also note that the coefficients are concentration dependent, unlike the binary pair values. We have calculated this for one composition but if you do this for another composition you will get a different set of values. The diffusivity matrix based on an average composition along the diffusion path is often used as the representative values and the composition dependency is ignored as an approximation.

Another point to note is the choice of the third component, that is, the species that is eliminated in the Stefan-Maxwell model. In the above case argon was eliminated and equations for the diffusion fluxes of the other two species are obtained from the diffusivity matrix. The coefficients will be different if another species, say hydrogen, is eliminated.

Multicomponent diffusion in liquids is often modeled by this approach and the D˜ matrix is fitted to experimental data. This is therefore more of an empirical approach. Often the non-ideal effects are not considered explicitly and lumped into the D˜ matrix. Similarly, diffusion in ternary solid alloys are often fitted in this manner.

The advantage of diffusion matrix formulation is that the models are analogous to a matrix version of Fick’s law. Hence linear algebra–based methods can be used to get a quick analytical solution. However the D˜ matrix is mole fraction dependent. Hence it has to be evaluated at some average mole fraction in the domain and further a constant value for this matrix has to be assigned. Such a model is called the linearized model, first introduced in the field by Toor (1957). On the other hand, in the direct solution method no such assumption is needed, but the problem has to be solved by numerial methods as shown in Section 15.2.

15.2 What is the basis for the Wilke equation for the pseudo-binary diffusion coefficient?

15.3 Under what conditions is the Wilke equation an exact representation of the Stefan-Maxwell model?

15.4 When is the exponential matrix-based method not suitable for solution of multicomponent diffusion problems?

15.5 What are reverse diffusion and osmotic diffusion?

15.6 If two independent reactions take place and there are five species, how many of the species fluxes are independent?

15.7 Define a diffusivity matrix and distinguish its components from binary pair diffusion coefficients.

15.8 What is the difference between D₁₂ and D₁₂?

15.9 Can D₁₁ be non-zero? Can D₁₁ be non-zero?

15.10 What is the implication of D₁₂? Can it be zero?

15.2 Comparison of Stefan-Maxwell model with Wilke model for ternary evaporation. Compare the results in exercise problem 1 with the model using a pseudo-binary diffusivity value for acetone. The pseudo-binary diffusivity can be calculated from the correlation given by Wilke.

15.3 Evaporation of a binary mixture: expm-based code. Write MATLAB code to solve Equations 15.22 and 23 for the unknowns N_A and N_B. You will need to write a function m-file to be used in FSOLVE, which takes in trial values of N_A and N_B, calculates the A and R matrices based on these values, and returns two equations based on Equations 15.22 and 15.23 as the function values. FSOLVE will then iterate using this function program to find N_A and N_B.

Test the results for the data given in Example 15.2.

15.4 Arnold cell analysis for a binary liquid. A binary mixture of A and B is contained in a tube with a starting level of H₀. Over time evaporation proceeds and the level changes with time. Develop a model to calculate the level change in the tube. Note that the mass balances for A and B in the liquid are needed since they change in different manners with time. Thus the liquid will get enriched with the less volatile compound.

15.5 CO diffusion to a catalytic surface followed by a heterogeneous reaction. Catalytic oxidation of CO is an important reaction in pollution prevention. The reaction scheme is

O₂(A) + 2CO(B) → 2CO₂(C)

Set up the Stefan-Maxwell model for this problem. State the determinacy condition and simplify the equations into two differential equations for the mole fractions of any two of these species. Calculate the solution for the mole fraction profiles and find the values of the fluxes using the matrix method and the BVP method. Assume fast reaction at the catalyst surface.

15.6 Rank of a stoichiometric matrix to find the invariant relations between the component fluxes. Examine how the rank of the stoichiometric matrix can be used to reduce the number of equations to be solved. For example, if there are ns components and nr equations we can show that only ns – nr independent mass balance equations are needed. The remaining variables form an invariant that connects the flux of the selected key components to those of the non-key components. Write MATLAB code to find the invariant given a stoichiometric matrix.

15.7 Methane reforming in a porous catalyst. Extend the analysis in Section 15.2 to two reactions that are applicable for steam reforming of methane. The first reaction is

CH₄ + H₂O CO + 3H₂

followed by the water-gas shift reaction. Kinetic and diffusion parameters can be found in the work by Haynes (1984) or other sources.

15.8 D˜ matrix values for hydrogen-methane-argon mixture. Consider the calculation of a generalized diffusion coefficient (

D matrix) for a gas mixture of hydrogen (1), methane (2), and argon (3). The following coefficient values are reported in Cussler (2009) at 298 K:

D˜=(0.76−0.010.120.25)

These values are for a composition of x₁ = 0.2 and x₂ = 0.2. The units are cm²/s. Argon was used as the species that was eliminated from the Stefan-Maxwell equation.

Verify the results if the binary pair values are D₁₂ = 0.726; D₁₃ = 0.902 and D₂₃ = 0.218 at 307 K temperature. Units are cm²/s.

15.9 Effect of composition numbering on the Fick matrix D˜. In the matrix calculation of D˜, a particular species n chosen for elimination is usually referred to as the solvent. For example, in the above example argon was chosen as the reference. The choice of “solvent” species is arbitrary but it can have an effect on the coefficient and the structure of the resulting matrix. For this exercise use argon (1), methane (2), and hydrogen (3). Eliminate hydrogen rather than argon, which was done in the previous exercise. Use the same composition as earlier. Show that the D˜ matrix is now

D˜=(0.64−0.39−0.120.37)

15.10 Transient profiles in a two bulb apparatus. Derive the solutions for transient concentration profiles in the two bulb apparatus (Example 6.4 in the text) for a binary case and show that the multicomponent case can be derived as an extension of this. What assumption is implicit in extending the binary case to the multicomponent case?