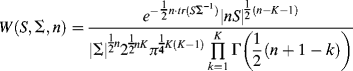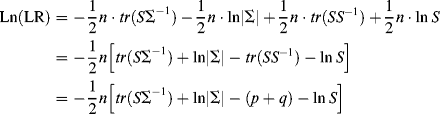Appendix 1.B Maximum Likelihood Function for SEM

In SEM model estimation, attention is directed to the sample distribution of the observed variance/covariance matrix S. If a random sample is selected from a multivariate normal population, the likelihood of finding a sample with variance/covariance matrix S is given by the Wishart distribution (Wishart, 1928):

(1.33)

where S is the sample variance/covariance matrix, is the population variance/covariance matrix, n = N − 1 (where N is sample size), K is the number of variables, and is the gamma function. Note that all the terms in Equation (1.33), except those involving , are constant. Since we are only interested in maximizing the function rather than calculating the precise value of the function, all the constant terms in Equation (1.33) can be combined into one constant term C, thus the equation can be simplified to:

(1.34)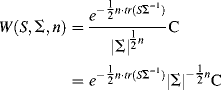

For a model that fits data perfectly, . As such, the ratio of the Wishart function of the specified model to that of the perfect model is:

(1.35)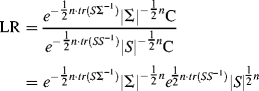

Taking a natural logarithm, we have

(1.36)

Since a minus sign precedes the right-hand side of Equation (1.36), maximizing Equation (1.36) is equivalent to minimizing the function in brackets:

(1.37)

where or F_ML is called the minimum discrepancy function, which is the value of the fitting function evaluated at the final estimates (Hayduk, 1987).

Notes

1. For a one-factor CFA model with three indicators, there are 3(3 + 1)/2 = 6 observed variances/covariances. When covariance structure (COVS) is analyzed, six free parameters: two factor loadings (one loading is fixed to 1.0), one variance of the factor, and three variances of the error terms; thus degrees of freedom (df) = 0.

2. LISREL, standing for linear structural relationship, was the first computer software for SEM, written by Drs Karl Jöreskog and Dag Sörbom from the University of Uppsala, Sweden.

3. The variance/covariance matrix for the latent endogenous variables η need not be estimated from modeling since it can be calculated as: Var () = Var [()/(I − )].

4. Data points usually refer to the number of variances and covariances among the observed variables; however, when mean and covariance structures (MACS) are analyzed, the means of the observed variables will be counted in the data points.

5. Most of the existing SEM software/programs set the factor loading of the first observed indicator of a latent variable to 1.0 by default.

6. In most SEM computer programs, model is defined as = f_ML(N − 1), but it is defined as = f_ML(N) in Mplus.

7. The noncentrality parameter is estimated as ( − df) [if < df, then set ( − df) = 0]. When model equals the df, the model fit is considered perfect. When a model is incorrectly specified, the model statistic would follow a noncentral distribution that can be approximately considered as a result of the central being shifted to the right by ( − df) units. As such, the noncentrality parameter can be considered as an index that reflects the degree to which a model fails to fit data. The larger the ( − df), the worse the model fit; the smaller the ( − df), the better the model fit.