3 Visual Cryptography for Multiple Secrets

Visual cryptography proposed by Naor and Shamir [7] discloses the possibility for using human visual ability to perform the decryption process. Specifically, one secret image is encoded into two shares that are seemingly random pictures. By xeroxing them onto transparencies, the dealer distributes the two random transparencies to two participants (one share for each participant). Each participant cannot tell the secret from his own transparency, but when the two participants superimpose their transparencies pixel by pixel, they recognize the secret from the superimposed result by their visual system. Neither computational devices nor cryptographic knowledge is required for the decryption process.

With such an interesting characteristic that the decryption process is by the human visual system only, instead of any computational device, visual cryptography attracts much attention from researchers. In particular, it is much useful in situations where computing devices are not available or not possible to use. Naor and Shamir [7] first presented k out of n visual secret-sharing schemes, which ensure that the secret is concealed from groups of less than k participants, while it can be seen by groups of at least k participants when they stack their shares altogether. Since this pioneer research, many theoretical results on the construction or contrast (the relative difference between the reconstructed white and black pixels in the superimposed image) of visual secret sharing schemes for binary images have been proposed in the literature [1, 10, 11, 2]. Some studies [4, 5, 9] focused on the practical realization of visual cryptographic schemes for gray-level or color images. So far, the above-mentioned results concern sharing “one” secret in a visual sense.

Wu and Chen [12] might be the first researchers to consider the problem of sharing two secret images in two shares in visual cryptography. They concealed two secret binary images into two seemingly random shares, namely S₁ and S₂, such that the first secret can be seen by stacking the two shares, denoted by S₁ ⊗ S₂, and the second secret can be obtained by Sθ1⊗S2 $S_{1}^{θ} \otimes S_{2}$ where θ denotes the superimposition operation and Sθ1 $S_{1}^{θ}$ is the result of rotating S₁ θ counterclockwise. S₁ and S₂ are in the shape of squares of the same size. In order to align the encoded pixels on S₁ and S₂ as well as on Sθ1 $S_{1}^{θ}$ and S₂, they designed the rotation angle θ to be 90°. Nevertheless, it is easy to obtain one that can be 180° or 270°.

Wu and Chang [13] refined the idea of Wu and Chen [12] by consciously designing the encoded shares to be circles so that the restrictions to the rotating angles (θ = 90°, 180°, or 270°) can be removed. Let the two encoded circle shares in their approach be denoted as A and B. The first secret is revealed by A ⊗ B, while the second secret is obtained by A^−θ ⊗ B where θ may be any angle within (0°, 360°) and A^−θ is the result of rotating A θ clockwise. Both of the studies successfully share two secrets in two shares in a visual sense.

Shyu et al. [8] devised an elegant algorithm to achieve the sharing of multiple sercte images using two circle shares. It is the first true approach that shares any general number of multiple secrets in two shares. Consider x secret images. Consider a set of x ≥ 2 secret images. Their scheme produces two circle shares A and B such that none of them individually leaks any secret and the x secrets can be obtained one by one A ⊗ B, A^θ ⊗ B, A^2θ ⊗ B,…, A^(x−1)θ⊗ B where A⁽ⁱ−^1)θ is the result of rotating A⁽ⁱ−^1)θ counterclockwise for 1 ≤ i ≤ x for θ = 360^θ /x and A⁰° − A This is the first true result of sharing multiple secrets in visual cryptography for any× ≥ 2 secrets in two shares. Their pixel expansion is 2x, which is the best result so far in the model that each pixel would be expanded.

Based on a different set of encoding patterns, Feng et al. [3] developed another scheme to achieve the same goal using two cylinder shares. The pixel expansion needed is 3x.

In this chapter, we introduce these interesting algorithms. The rest of the paper is organized as follows. In Section 3.2, we briefly review the visual one-secret sharing scheme in two shares proposed by Naor and Shamir [7]. The visual two-secret sharing scheme by Wu and Chen [12] and Wu and Chang [13] are discussed in Sections 3.3.1 and 3.3.2, respectively. The schemes for visual multisecret are examined in Section 3.4 in which the experimental results and discussions are also presented. Section 3.5 gives some concluding remarks.

3.2 Naor and Shamir’s Basic Visual Secret Sharing Scheme

The basic idea of Naor and Shamir’s encoding scheme [7] for sharing a single pixel, say p, in a binary image P into two shares s₁ and s₂ is illustrated in Table 3.1. If p is white, the dealer randomly chooses one of the first two rows of Table 3.1 to encode s₁ and s₂. If p is black, the dealer randomly chooses one of the last two rows in Table 3.1 to encode s₁ and s₂. The possibilities of the two encoding cases are equally likely to occur, independently of whether the original pixel is black or white. Thus, neither s₁ nor s₂ exposes any clue about the binary color of p. When these two shares are stacked together, i.e., s₁ ⊗ s₂, two black subpixels appear if p is black, while one black subpixel and one white subpixel appear if p is white as indicated in the rightmost column in Table 3.1. Based upon the contrast between these two kinds of reconstructed pixels, our visual system can tell whether p is black or white by observing s₁ ⊗ s₂

Note that s₁ (or s₂) in Table 3.1 is not a single pixel, but two subpixels. We call s₁ (or s₂) an extended block and the pair (s₁, s₂) the pair of two extended blocks with respect to p. The number of the subpixels in each of the two extended blocks (s₁, s₂) for encoding p is referred to as the pixel expansion. In Table 3.1, the pixel expansion is 2. In realistic implementations, it may be chosen as 4 (= 2 × 2) in order to retain the aspect ratio of the original secret image. Since there are six possible patterns for a 2 × 2 extended block, all pairs of two extended blocks (s₁, s₂)’s for encoding a specific binary pixel p (visual one-secret sharing) are summarized in Table 3.2.

When p is white (black), the dealer randomly chooses one of the first (last) six rows of Table 3.2 to encode p into s₁ and s₂. It is seen from the last column of Table 3.2 that the reconstructed pixel r = s₁ ⊗ s₂ may contain two white and two black subpixels if p is white, or all four black subpixels when p is black. When all pixels in p are encoded in this way, where each p’s random choice for encoding alternatives is independent, the encoded shares S₁ (containing all s₁’s) and S₂ (containing all s₂’s) are indeed random pictures, respectively. When S₁ and S₂ are superimposed, all of the four subpixels are black in the reconstructed blocks corresponding to each black pixel in P, while two subpixels are white and the other two are black corresponding to each white pixel in P. Based upon such a difference, our visual system recognizes the white and black pixels in P from S₁ ⊗ S₂. We say that the reconstructed image S₁ ⊗ S₂ recovers P.

Images

Table 3.1 Encoding a binary pixel p into two shares s₁ and s₂.

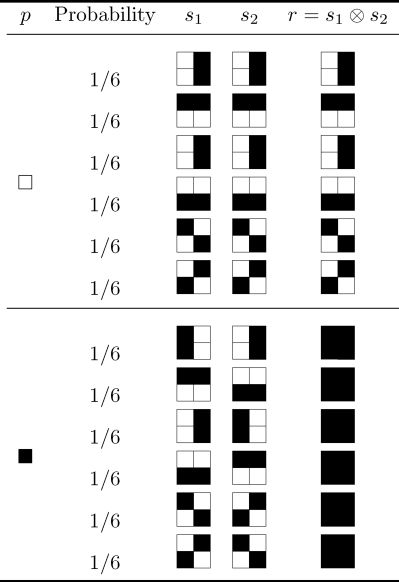
Images

Table 3_2 Implementing the visual one secret sharing scheme with a pixel expansion of 4.

Figure 3.1 shows the implementation results of the encoding scheme in Table 3.2. Figure 3.1(a) is a secret binary image P, Figures 3.1(b) and (c) are the two encoded shares S₁ and S₂ , which are random pictures revealing no information about P and Figure 3.1(d) illustrates the reconstructed image S₁ ⊗ S₂ that recovers P visually.

Images

FIGURE 3.1
Implementation results of visual one-secret sharing in two shares: (a) P, (b) S₁, (c) S2, (d) S₁ ⊗ S₂.

3.3 Visual Two-Secret Sharing Schemes

3.3.1 Wu and Chen’s Scheme

Following the research of Naor and Shamir, Wu and Chen [12] developed a visual secret sharing scheme that encrypts two secrets into two shares. Given two N× N (square) secret binary images P₁ and P₂, their scheme produces two shares, namely S₁ and S₂, which reveal no information about P₁ or P₂ individually. Yet when stacking S₁ and S₂, we obtain P₁ visually; moreover, when stacking S90°1 $S_{1}^{90 °}$ and S₂, we see P₂.

Consider a pair of pixels p₁ = P₁[i, j] and p₂ = P₂[u, v] in P₁ and P₂, respectively. We refer to (p₁, p₂) as the corresponding pixels of P₁ and P₂ if and only if i = u and j = v. Given a set of corresponding pixels (p₁, p₂),Wu and Chen’s encoding scheme for visual two-secret sharing in two shares is summarized in Table 3.3.

It is seen from Table 3.3 that each pair of corresponding pixels (p₁ , p₂) of (P₁, P₂) is encoded into extended blocks s₁ (as well as S90°1 $S_{1}^{90 °}$ ) and s₂ in which the pixel expansion is m = 4. Note that S90°1 $S_{1}^{90 °}$ is exactly the result of rotating s₁ 90° counterclockwise. We explain how Wu and Chen’s encoding scheme works by using a simple example. Assume that the two secret images P₁ and P₂ are composed in a square of 12 × 12 pixels. Then, the two encoded shares S₁ and S₂ are composed in a square of 48 × 48 (48 = 12 × 4) pixels. They first decompose S₁ into four triangle-like areas with an equal size as shown in Figure 3.2(a). All of the four areas are composed of an equal amount of extended blocks (2 × 2 pixels each), which are indexed as shown in Figure 3.2(b) where each triangle-like area contains 36 blocks. Let block j in area k be denoted as bkj $b_{j}^{k}$ for 1 ≤ k ≤ 4 and 1 ≤ j ≤ 36. The extended blocks in area I, b1j $b_{j}^{1}$ , are randomly selected out of those in Figure 3.2(c). Each block, say btj $b_{j}^{t}$ , in area II, III, IV is assigned to be the same as b1j $b_{j}^{1}$ in area I, that is, btj=b1j $b_{j}^{t} = b_{j}^{1}$ for t = 2, 3,4, and 1 ≤ j ≤ 36.

Let us pay attention to the four pixels at the top-right, top-left, bottom-left, and bottom-right corners in sequence (counterclockwise) in P₁ and P₂. Assume that those pixels in P₁ (P₂) are □, □, ■. ■ (□, ■. □, ■) as shown in Figure 3.3(a) and (Figure 3.3(b)). Assume that corresponding block at b126 $b_{26}^{1}$ at S₁ is randomly determined as then as mentioned bt26 $b_{26}^{t}$ is for 2 ≤ t ≤ 4 (see Figure 3.3(c)). The above-mentioned pixels in P₁ and P₂ constitute four sets of corresponding pixels: (□, □), (□, ■), (■, □), and (■, ■). Since bk26 $b_{26}^{k}$ in S₁ is for 1 ≤ k ≤ 4, according to Table 3.3 the four blocks b126, b226, b326 $b_{26}^{1}, b_{26}^{2}, b_{26}^{3}$ and b426 $b_{26}^{4}$ , in S₂ with respect to the four sets of the corresponding pixels are , and , respectively (see the 2nd, 6th, 10th, and 14th rows in column s₂ of Table 3.3). Figure 3.3(d) illustrates the encoding result of S₂. As expected, the four corners in the above-mentioned order in S₁ ⊗ S₂ reveal □, □, ■. ■, respectively (see Figure 3.3(e)) to our visual system. When S₁ is rotated as S90°1 $S_{1}^{90 °}$ as indicated in Figure 3.3(f), where all blocks are in the form of S90°1 $S_{1}^{90 °}$ , the four corresponding corners in S90°1⊗S2 $S_{1}^{90 °} \otimes S_{2}$ recover □, ■, □, ■, respectively (see Figure 3.3(g)). It is not hard to see that by encoding all pixels in S₁ and S₂ with respect to the corresponding pixels in P₁ and P₂ according to Table 3.3, P₁ and P₂ can be recovered by S₁ ⊗ S₂ and S90°1⊗S2 $S_{1}^{90 °} \otimes S_{2}$ , respectively.

Images

Table 3_3 Wu and Chen’s encoding scheme for visual two-secret sharing in two shares.

Images

FIGURE 3.2
Encoding S₁ in Wu and Chen’s scheme: (a) Four triangle-like areas. (b) Indexing the blocks in each of the four areas. (c) Blocks to be assigned.

Note that S₁ and S₂ are in the shape of squares of the same size. S₁ ⊗ S₂ reveals P₁, while Sθ1⊗S2 $S_{1}^{θ} \otimes S_{2}$ reveals P₂. Wu and Chen set θ to be 90°. It is easy to extend their idea to design θ as one of 90°, 180°, or 270°, but the other degrees are infeasible. This is because the rotated S1 (Sθ1) $S_{1} (S_{1}^{θ})$ cannot be aligned to S₂ pixel by pixel when θ ≠ 0°, 90°, 180°, or 270°. Except for the fact that it is restricted, there is another pitfall in their scheme: since the encoded pixels in each of areas I, II, III, and IV in S₁ are exactly the same, S₁ is not a random picture. In fact, only 1/4 shares of S₁ are purely random pictures.

3.3.2 Wu and Chang’s Scheme

Based upon the idea of Wu and Chen [12], Wu and Chang [13] devised another visual two-secret sharing scheme that allows the rotation angle to be an arbitrary one between 0° and 360° by adopting circle shares. Given an angle and two secret images P₁ and P₂, their approach produces two circle shares A and B such that any single A or B is a seemingly random picture that leaks nothing about P₁ or P₂; while A ⊗ B reconstructs P₁ and A−^θ ⊗ B recovers P₂ where A−^θ denotes the result of rotating A θ clockwise. Note that A−^θ ⊗ B is equivalent to A ⊗ B^θ. Intuitively, it is reasonable to choose circles as the encoded shares since they ease the correct alignments between A and B as well as A−^θ and B pixel by pixel where 0° < θ < 360°.

Images

FIGURE 65.3
Example for illustrating the idea of Wu and Chen [12]: (a) P₁, (b) P₂, (c) S₁, (d) S₂, (e) S₁ ⊗ S₂, (f) S90°1 $S_{1}^{90 °}$ , (g) S90°1⊗S2 $S_{1}^{90 °} \otimes S_{2}$ .

They deliberately decomposed circle share A into 360°/θ areas where each area contains an equal amount of 2 × 2 sector blocks. Figure 3.4(a) shows the four typical patterns for sector blocks, namely S11, S21, S31 $S_{1}^{1}, S_{1}^{2}, S_{1}^{3}$ , and S41 $S_{1}^{4}$ , used in their approach. That is, the whole circle share A is composed by all these four sector blocks. Note that S11 (S21, S31, S41) $S_{1}^{1} (S_{1}^{2}, S_{1}^{3}, S_{1}^{4})$ can be consciously regarded as the result of rotating S21 (S31, S41, S11, respectively) $S_{1}^{2} (S_{1}^{3}, S_{1}^{4}, S_{1}^{1}, respectively)$ 90° counterclockwise (or S21 $S_{1}^{2}$ can be consciously regarded as the result of rotating 90 clockwise). We say that S1,1 S (S2,1S, S3,1S, S4,1S, ) $S_{1}^{1,} S (S_{1}^{2,} S, S_{1}^{3,} S, S_{1}^{4,} S,)$ previous sector block is S41 (S11, S21, S31, respectively) $S_{1}^{4} (S_{1}^{1}, S_{1}^{2}, S_{1}^{3}, respectively)$ and its next sector block is S21 (S31, S41, S11, respectively) $S_{1}^{2} (S_{1}^{3}, S_{1}^{4}, S_{1}^{1}, respectively)$ as summarized in Figure 3.4(b).

Images

FIGURE 3.4
2 × 2 sector blocks for A in Wu and Chang’s approach: (a) 2 × 2 sector blocks for A, (b) prev(s) and next(s) of sector block s.

Let the number of areas in circle share A be α(= 360°/θ) and the number of sector blocks in each area be ß. These a areas are indexed clockwise. Let akj $a_{j}^{k}$ be the jth sector block in area k in A, 1 ≤ j ≤ ß and 1 ≤ k ≤ α. At first, the ß sector blocks in the first area are randomly selected out of those in Figure 3.4(a). Then, sector blocks in area t are defined according to those in area t − 1 by assigning atj $a_{j}^{t}$ as the next sector block of at−1j, i.e., atj=next(at−1j) $a_{j}^{t - 1}, i .e ., a_{j}^{t} = n e x t (a_{j}^{t - 1})$ (or at−1j, = prev(atj)) $a_{j}^{t - 1}, = p r e v (a_{j}^{t}))$ for 1 ≤ j ≤ ß and 2 ≤ t ≤ α.

Given a pair of corresponding pixels p₁ and p₂ in P₁ and P₂, respectively, each sector block bkj $b_{j}^{k}$ in B is determined by p₁, p₂, and the corresponding block akj $a_{j}^{k}$ in A for 1 ≤ j ≤ ß and 1 ≤ k ≤ α. Table 3.4 summarizes such an encoding scheme.

Note that in Wu and Chen’s scheme each extended block s₂ in S₂ would be superimposed with s₁ and S90°1 $S_{1}^{90 °}$ when s₁ is rotated 0° (or fixed) and 90° counterclockwise, respectively. In Wu and Chang’s scheme, each sector block bkj $b_{j}^{k}$ in B is superimposed with akj $a_{j}^{k}$ in area k and ak−1j $a_{j}^{k - 1}$ in k’s previous area k − 1 when A is rotated 0° and θ clockwise where ak−1j=prev(akj) (or akj=next(ak−1j)) $a_{j}^{k - 1} = p r e v (a_{j}^{k}) (or a_{j}^{k} = n e x t (a_{j}^{k - 1}))$ . Note that ak−1j $a_{j}^{k - 1}$ is the result of rotating akj 90° $a_{j}^{k} 90 °$ counterclockwise (or akj $a_{j}^{k}$ is the result of rotating ak−1j 90° $a_{j}^{k - 1} 90 °$ clockwise; see Figure 3.4). That means the result of A−^θ ⊗ B in Wu and Chang’s scheme emulates that of S90°1⊗S2 $S_{1}^{90 °} \otimes S_{2}$ in Wu and Chen’s scheme. There is no restriction for θ to be 90°, 180°, or 270° merely. Yet there exist some inconsistent situations in some of the areas in A^−θ ⊗ B when α = 360°/θ > 4. Interested readers refer to Ref. [13] for details.

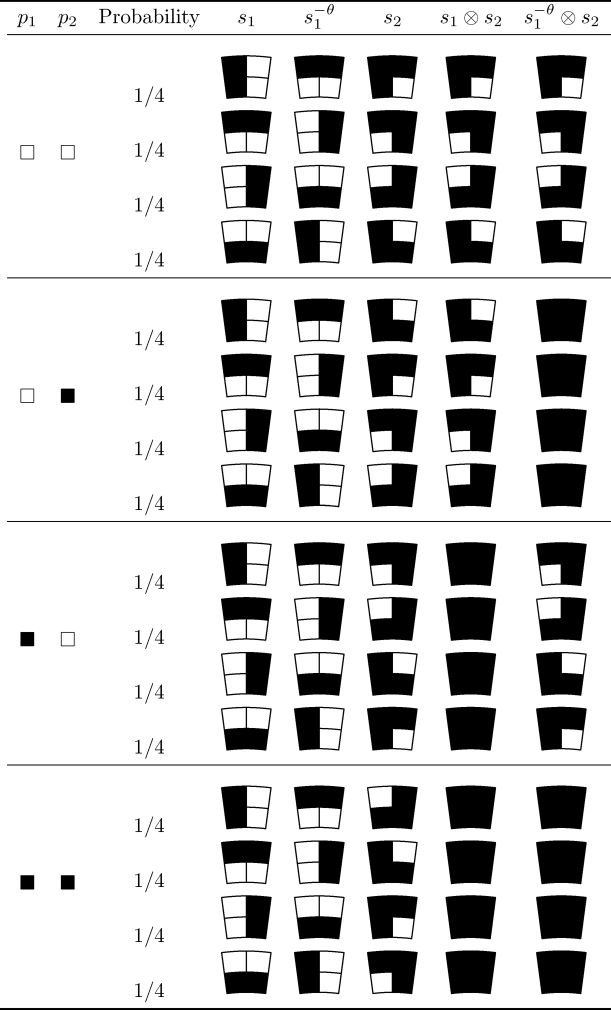
Images

Table 3_4 Wu and Chang’s encoding scheme for visual two-secret sharing in two shares.

As mentioned above, square share S₁ in Wu and Chen’s scheme is not a totally random image. Strictly speaking, neither is circle share A in Wu and Chang’s scheme due to the reason that sector block atj $a_{j}^{t}$ is assigned as next(at−1j) $(a_{j}^{t - 1})$ (i.e., the result of rotating at−1j $a_{j}^{t - 1}$ 90° clockwise) for 2 ≤ t ≤ α; that is, only sector block a1j $a_{j}^{1}$ in the first area is randomly determined from those in Figure 3.4(a) for 1 ≤ j ≤ ß, while the other areas are not. Furthermore, sector blocks in the first area of circle share A (see Figure 3.4(a)) in Wu and Chang’s scheme (or extended blocks in the first area of square share S₁ (see Figure 3.2(c)) contain only four patterns, instead of six, which is the number of all possible combinations for four subpixels with two white and two black subpixels (see Table 3.2).

3.4 Visual Multiple-Secret Sharing Schemes

Both of the above-mentioned schemes accomplish visual secret sharing for only two secrets in two shares. In this section we discuss two more generalized visual secret sharing scheme for x ≥ 2 secrets in two shares by Shyu et al. [8] and Feng et al. [3] in Sections 3.4.1 and 3.4.2, respectively.

3.4.1 Shyu et al.’s Scheme

3.4.1.1 Informal Description

Let us start by using a simple example. Assume that the number of secret images to be shared is x = 3. Let P₁, P₂, and P₃ be the three binary secret images with the same size h × w. Let p₁, p₂, and p₃ denote the corresponding pixels in P₁, P₂, and P₃, respectively. Let A and B denote the two circle shares encoded by the scheme. Our aim is to assure A ⊗ B recovers P₁, A120°⊗B $A^{120 °} \otimes B$ recovers P₂, and A240°⊗B $A^{240 °} \otimes B$ recovers P₃.

Since there are three secrets, we decompose circle share A and B into three (x = 3) chord-areas (chords for short), respectively, in which the angle of each chord extends up to 120°(= 360°/x = 360°/3). Each chord is divided into a set of 2 × 3 (2 × x) chord blocks. Let the number of 2 × 3 blocks in each chord be ß. Let akj $a_{j}^{k}$ and bkj $b_{j}^{k}$ denote block j of chord k in A and B, respectively, 1 ≤ j ≤ ß and 1 ≤ k ≤ 3(= x). The chords are indexed clockwise and the divided blocks in A and B are indexed as shown in Figures 3.5(a) and (b), respectively. We call akj $a_{j}^{k}$ and bkj $b_{j}^{k}$ the corresponding blocks in A and B.

3.4.1.2 Encoding Circle Share A

We first define three 2 × 3 elementary blocks, namely S1A, S2A $S_{A}^{1}, S_{A}^{2}$ , and S3A $S_{A}^{3}$ , for circle share A as shown in Figure 3.6. That is, these elementary blocks are the basic constituents of A and there are one white and five black subpixels in each of the elementary blocks.

In order to guarantee the randomness when using SkA $S_{A}^{k}$ as a constituent of A for 1 ≤ k ≤ 3, we permute the subpixels within SkA $S_{A}^{k}$ before assigning SkA $S_{A}^{k}$ as a constituent block in A. Let ∑ = (σ₁, σ₂, σ₃, σ₄, σ₅, σ₆) be a permutation of 1, 2, 3,4, 5, 6 (in which 6 = 2x = 2 × 3). We define a function permute(s, ∑) rearranging the subpixels in elementary block s by permutation ∑. Figure 3.7(a) shows a certain typical ordering of the subpixels in a 2× 3 elementary block s and Figure 3.7(b) shows the result of permute(s, ∑) with ∑ = (3, 5,1, 6, 2,4). Note that the order of the subpixels in the elementary block s can be defined arbitrarily.

We call the set of three blocks (a1j, a2j, a3j) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3})$ the related blocks of the three chords in A for 1 ≤ j ≤ ß. Obviously, there are totally ß sets of the related blocks in A. For a certain set of related blocks (a1j, a2j, a3j) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3})$ , we generate one permutation, denoted as ∑_j, and assign akj $a_{j}^{k}$ to be permute (SkA, Σj) $(S_{A}^{k}, Σ_{j})$ for 1 ≤ k ≤ 3 and 1 ≤ j ≤ ß. That is,

(a 1 j, a 2 j, a 3 j) = (p e r m u t e (s 1 A Σ j), p e r m u t e (s s A, Σ j), p e r m u t e (s 3 A, Σ j)) (3.1)

$(a_{j}^{1}, a_{j}^{2}, a_{j}^{3}) = (p e r m u t e (s_{A}^{1} Σ_{j}), p e r m u t e (s_{A}^{s}, Σ_{j}), p e r m u t e (s_{A}^{3}, Σ_{j})) (3.1)$

for 1 ≤ j ≤ ß.

For the purpose of illustration, we show how the first set of the related blocks (a11, a21, a31) $(a_{1}^{1}, a_{1}^{2}, a_{1}^{3})$ in A is encoded. Assume that ∑₁ = (1, 2, 3,4, 5, 6). Figure 3.8(a) exposes the results of encoding (a1j, a2j, a3j) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3})$ in A. Note that for this particular ∑₁ permute (SkA, Σ1)=SkA $(S_{A}^{k}, Σ_{1}) = S_{A}^{k}$ for 1 ≤ k ≤ 3. In real implementation, a new random permutation ∑_j is adopted when encoding (a1j, a2j, a3j) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3})$ in A for each j, 1 ≤ j ≤ ß. Figures 3.8(b) and (c) show the results of A120° $A^{120 °}$ and A240° $A^{240 °}$ , respectively.

Let [k, j] denote the absolute location with respect to block j of chord k in a circle share (see Figure 3.9) and A^θ [k, j] denote the content of block [k, j] in A^θ (i.e., the results of rotating A θ counterclockwise) where 1 ≤ k ≤ 3 (= x), 1 ≤ j ≤ ß and θ = 120°(= 360°/3)(A0°[k,j]=A[k,j]) $(A^{0 °} [k, j] = A [k, j])$ . The relationship among the related blocks is easily seen from Figures 3.8 and 3.9:

Images

FIGURE 70.3
Decomposing circle shares A and B into chords, which are further divided into blocks: (a) A, (b) B.

Images

FIGURE 71.3
Elementary blocks for circle share A for sharing 3 secrets: (a) S1A $S_{A}^{1}$ , (b) S2A $S_{A}^{2}$ , (c) S3A $S_{A}^{3}$ .

Images

FIGURE 3.7
Subpixels in 2 × 3 elementary block s and permute(s, ∑): (a) a certain ordering of the subpixels in s, (b) the ordering of those in permute(s, ∑) where ∑ = (3, 5,1, 6, 2, 4).

A [1, j] = a 1 j, A [2, j] = a 2 j, A [3, j] = a 3 j, A 120 ° [1, j] = a 2 j, A 120 ° [2, j] = a 3 j, A 120 ° [3, j] = a 1 j, A 240 ° [1, j] = a 3 j A 240 ° [2, j] = a 1 j A 240 ° [3, j] = a 2 j (3.2)

$\begin{array}{l} A [1, j] = a_{j}^{1}, & A^{120 °} [1, j] = a_{j}^{2}, & A^{240 °} [1, j] = a_{j}^{3} \\ A [2, j] = a_{j}^{2}, & A^{120 °} [2, j] = a_{j}^{3}, & A^{240 °} [2, j] = a_{j}^{1} \\ A [3, j] = a_{j}^{3}, & A^{120 °} [3, j] = a_{j}^{1}, & A^{240 °} [3, j] = a_{j}^{2} \end{array} (3.2)$

for 1 ≤ j ≤ ß.

3.4.1.3 Encoding Circle Share B

First of all, with regard to the three given h × w secret images P₁, P₂, and P₃, we divide P_i evenly into ß = h× (w/3) = h × (w/x)strips. Let (pi)kj ${(p_{i})}_{j}^{k}$ denote the jth pixel of strip k in P_i and (p1, p2, p3)kj=((p1)kj, (p2)kj, (p3)kj) ${(p_{1}, p_{2}, p_{3})}_{j}^{k} = ({(p_{1})}_{j}^{k}, {(p_{2})}_{j}^{k}, {(p_{3})}_{j}^{k})$ be the jth corresponding pixels of strip k for (P₁, P₂, P₃) where 1 ≤ j ≤ ß and 1 ≤ i, k ≤ 3. Each block, say bkj $b_{j}^{k}$ , in B is determined according to the related blocks (a1j, a2j, a3j) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3})$ in A and the corresponding pixels (p1, p2, p3)kj ${(p_{1}, p_{2}, p_{3})}_{j}^{k}$ in (P₁, P₁, P₃) for 1 ≤ j ≤ ß and 1 ≤ k ≤ 3.

Consider a particular block b1j $b_{j}^{1}$ in the first chord of B. Note that the corresponding block a1j (a2j and a3j) $a_{j}^{1} (a_{j}^{2} and a_{j}^{3})$ in A (A¹²⁰° and A²⁴⁰° , respectively) is a permuted result of elementary block S1A $S_{A}^{1}$ (S2A $S_{A}^{2}$ and S3A $S_{A}^{3}$ , respectively) according to ∑_j, which is decided in run time. The encoding scheme for b1j $b_{j}^{1}$ before run time is essentially based upon (S1A, S2A, S3A) $(S_{A}^{1}, S_{A}^{2}, S_{A}^{3})$ and (p1, p2, p3)1j ${(p_{1}, p_{2}, p_{3})}_{j}^{1}$ as summarized in Table 3.5.

It is observed from Table 3.5 that given a set of corresponding pixels (p₁, p₂, p₃), the results of S1A⊗SB (S2A⊗SB, S3A⊗SB) $S_{A}^{1} \otimes S_{B} (S_{A}^{2} \otimes S_{B}, S_{A}^{3} \otimes S_{B})$ reveals p₁ (p₂, p₃, respectively) to our visual system. For instance, consider the third row of Table 3.5 where (p₁, p₂, p₃) = (□, ■, □). When the related blocks in A are in their elementary forms S1A, S2A $S_{A}^{1}, S_{A}^{2}$ , and S3A $S_{A}^{3}$ , we design s_B to be so that both S1A⊗SB $S_{A}^{1} \otimes S_{B}$ and S3A⊗SB $S_{A}^{3} \otimes S_{B}$ reveal one white and five black subpixels, while S2A⊗SB $S_{A}^{2} \otimes S_{B}$ show six black subpixels. Our eyes recognize S1A⊗SB $S_{A}^{1} \otimes S_{B}$ and S3A⊗SB $S_{A}^{3} \otimes S_{B}$ as white, while S2A⊗SB $S_{A}^{2} \otimes S_{B}$ as black. That means (p₁, p₂, p₃) is recovered by (S1A⊗SB, S2A⊗SB, S3A⊗SB) $(S_{A}^{1} \otimes S_{B}, S_{A}^{2} \otimes S_{B}, S_{A}^{3} \otimes S_{B})$ in a visual sense.

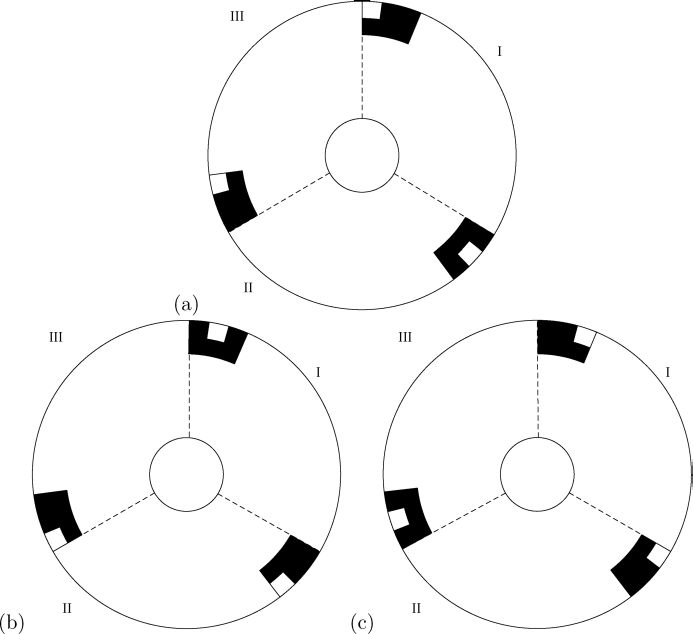
Images

FIGURE 72.3
Encoding the first three blocks in each of the three chords by ∑₁ in A: (a) A, (b) A¹²⁰°, (c) A²⁴⁰°.

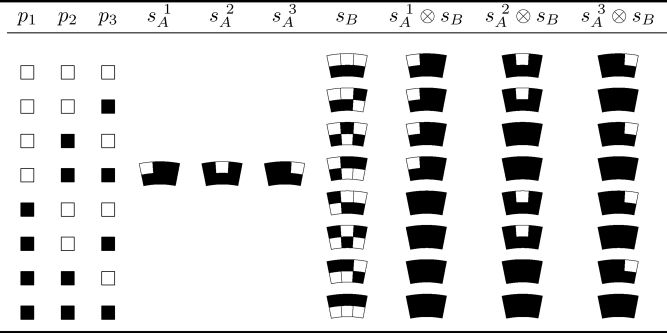
Images

FIGURE 73.3
Absolute location of block [1, j], [2, j], and [3, j].

Images

Table 3_5 Encoding a set of corresponding pixels (p1, p2, p3)1j ${(p_{1}, p_{2}, p_{3})}_{j}^{1}$ into a1j (a2j and a3j) $a_{j}^{1} (a_{j}^{2} and a_{j}^{3})$ and b1j $b_{j}^{1}$ in terms of S1A (S2A, S3A, respectively) $S_{A}^{1} (S_{A}^{2}, S_{A}^{3}, respectively)$ and s_B in the first chords of A and B, respectively for visual 3-secret sharing.

In actual implementation, the set of three related blocks (a1j, a2j, a3j) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3})$ in A is deliberately assigned as (permute(s1A, Σj) $(p e r m u t e (s_{A}^{1}, Σ_{j})$ , permute(s2A, Σj) $(s_{A}^{2}, Σ_{j})$ ,permute(s3A, Σj)) $(s_{A}^{3}, Σ_{j}))$ so that we only need to assign b1j $b_{j}^{1}$ to be permute(SB, Σj) $(S_{B}, Σ_{j})$ to preserve the superimposition results designed in Table 3.5. Then, when we superimpose a1j $a_{j}^{1}$ and b1j $b_{j}^{1}$ , we identify (p1)1j ${(p_{1})}_{j}^{1}$ form a1j⊗b1j $a_{j}^{1} \otimes b_{j}^{1}$ . When we rotate A 120° counterclockwise, b1,j S $b_{j}^{1,} S$ corresponding block in A¹²⁰° turns out to be a2j $a_{j}^{2}$ (i.e., A¹²⁰° [1, j], see formula (3.2) and Figure 3.9) and a2j⊗b1j $a_{j}^{2} \otimes b_{j}^{1}$ reveals (p2)1j ${(p_{2})}_{j}^{1}$ in a visual sense. Likewise, when rotating A 240° counterclockwise, b1,j S $b_{j}^{1,} S$ corresponding block in A²⁴⁰° is a3j $a_{j}^{3}$ and a3j⊗b1j $a_{j}^{3} \otimes b_{j}^{1}$ reveals (p3)1j ${(p_{3})}_{j}^{1}$ . In general, when rotating A (i − 1)θ counterclockwise we recognize aij⊗b1j $a_{j}^{i} \otimes b_{j}^{1}$ as (pi)1j ${(p_{i})}_{j}^{1}$ in the first chord of A^{(i− 1)θ} ⊗ B by our visual system for 1 ≤ i ≤ 3(= x) and θ = 120°(= 360°/x).

We call the blocks in column s_B of Table 3.5 the elementary blocks circle share B for sharing 3 secrets, which consists of three white and three black subpixels. They are named by , S0B, S1B,…, S7B $S_{B}^{0}, S_{B}^{1}, \dots, S_{B}^{7}$ , in sequence as indicated in Figure 3.10. When we denote □ as 0 and ■ as 1, the superscript l of SlB $S_{B}^{l}$ is equal to the code formed by p₁p₂p₃ in binary, i.e. l = blod(p₁p₂p₃) where btod(b) is a function that returns the decimal representation of a binary number b. It means that based upon Table 3.5, once (a1j, a2j, a3j) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3})$ is assigned to be (S1A, S2A, S3A) $(S_{A}^{1}, S_{A}^{2}, S_{A}^{3})$ and b1j $b_{j}^{1}$ is encoded to be sbtod(p1p2p3)B $s_{B}^{b t o d (p_{1} p_{2} p_{3})}$ (specifically, (a1j,a2j,a3j)=(permute(S1A, Σj),permute(S2A, Σj),permute(S3A, Σj)) $(a_{j}^{1}, a_{j}^{2}, a_{j}^{3}) = (p e r m u t e (S_{A}^{1}, Σ_{j}), p e r m u t e (S_{A}^{2}, Σ_{j}), p e r m u t e (S_{A}^{3}, Σ_{j}))$ and b1j=permute(Sbtod(p1p2p3)B, Σj) $b_{j}^{1} = p e r m u t e (S_{B}^{b t o d (p_{1} p_{2} p_{3})}, Σ_{j})$ in practical implementation with respect to give (p1,p2,p3)1j,(a1j⊗b1j,a2j⊗b1j,a3j⊗b1j) ${(p_{1}, p_{2}, p_{3})}_{j}^{1}, (a_{j}^{1} \otimes b_{j}^{1}, a_{j}^{2} \otimes b_{j}^{1}, a_{j}^{3} \otimes b_{j}^{1})$ recovers (p1,p2,p3)1j ${(p_{1}, p_{2}, p_{3})}_{j}^{1}$ .

Images

FIGURE 3.10
Elementary blocks of share B for sharing 3 secrets: (a) S0B $S_{B}^{0}$ (b) S1B $S_{B}^{1}$ , (c) S2B $S_{B}^{2}$ , (d) S3B $S_{B}^{3}$ , (e) S4B $S_{B}^{4}$ , (f) S5B $S_{B}^{5}$ , (g) S6B $S_{B}^{6}$ , (h) S7B $S_{B}^{7}$ .

Now, we take the instances in Figure 3.11, in which the first three pixels of the three divided strips in P_i are depicted for 1 ≤ i ≤ 3, as an example to show how the corresponding blocks in B are encoded. From Figure 3.11, we have (p1,p2,p3)11=(□,■,□). ${(p_{1}, p_{2}, p_{3})}_{1}^{1} = (□, ■, □) .$ According to Table 3.5, the elementary block for b11 $b_{1}^{1}$ is chosen to be Sbtod(p1p2p3)B=Sbtod(010)B=S2B $S_{B}^{b t o d (p_{1} p_{2} p_{3})} = S_{B}^{b t o d (010)} = S_{B}^{2}$ . Since in practical implementation, b1,1 S $b_{1}^{1,} S$ ’s corresponding block a11 (a21, a31) $a_{1}^{1} (a_{1}^{2}, a_{1}^{3})$ in A (A¹²⁰°, A²⁴⁰° , respectively) has been encoded as permute(s1A,∑ 1) (permute(s2A,∑ 1),permute(s3A,∑ 1)) $(s_{A}^{1}, \sum_{1}) (p e r m u t e (s_{A}^{2}, \sum_{1}), p e r m u t e (s_{A}^{3}, \sum_{1}))$ , respectively), the same permutation ∑₁ should be adopted for encoding b11 $b_{1}^{1}$ to preserve the superimposition result of s1A ⊗sB(s1A ⊗sB and s1A ⊗sB) $s_{A}^{1} \otimes s_{B} (s_{A}^{1} \otimes s_{B} and s_{A}^{1} \otimes s_{B})$ , respectively). Let us simply set ∑₁ = {1, 2, 3,4, 5, 6}. Therefore, b11 $b_{1}^{1}$ is encoded as permute (s2B, ∑ 1) $(s_{B}^{2}, \sum_{1})$ as show in Figure 3.12. It is easily seen that

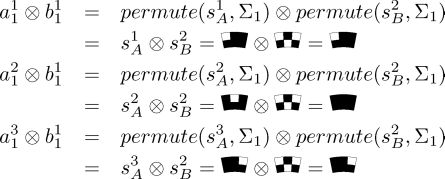
Images

FIGURE 3.11
Instances of the first three pixels of the three strips in (a) P₁, (b) P₂, and (c) P₃.

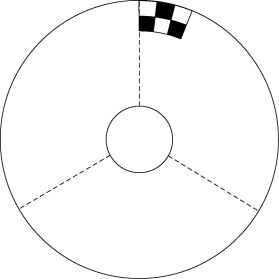
Images

FIGURE 3.12
Encoding b11 $b_{1}^{1}$ in B.

Therefore, the first blocks in the first chords of A ⊗ B, A¹²⁰° ⊗ B, and A²⁴⁰° ⊗ B reconstruct (p1)11 ${(p_{1})}_{1}^{1}$ (□), (p2)11 ${(p_{2})}_{1}^{1}$ ; (■), and (p3)11 ${(p_{3})}_{1}^{1}$ (□), respectively.

In summary, given a certain (p1,p2,p3)1j ${(p_{1}, p_{2}, p_{3})}_{j}^{1}$ in the first strips of (p1,p2,p3),bij $(p_{1}, p_{2}, p_{3}), b_{j}^{i}$ is encoded as permute(sbtod(p1,p2,p3)B,∑ j) $(s_{B}^{b t o d (p_{1}, p_{2}, p_{3})}, \sum_{j})$ where ∑_j is a random permutation for 1 ≤ j ≤ ß. It is noted that for a specific black b1j $b_{j}^{1}$ in the first chord of B, when A is rotated 0°, 120°, and 240° counterclockwise, the blocks that are superimposed onto b1j $b_{j}^{1}$ are a1j,a2j $a_{j}^{1}, a_{j}^{2}$ , and a3j $a_{j}^{3}$ , respectively where akj=permute(skA, ∑ j) $a_{j}^{k} = p e r m u t e (s_{A}^{k}, \sum_{j})$ for 1 ≤ j ≤ ß and 1 ≤ k ≤ 3.

Now, consider a certain block b2j $b_{j}^{2}$ in the second chord of B. When A is rotated 0°, 120°, and 240° counterclockwise, the blocks that are superimposed onto b2j $b_{j}^{2}$ are a2j, a3j $a_{j}^{2}, a_{j}^{3}$ , and a1j $a_{j}^{1}$ accordingly (see Figure 3.9 and formula (3.2)). Thus, to recover a given set of (p1,p2,p3)2j ${(p_{1}, p_{2}, p_{3})}_{j}^{2}$ , we should assure that s2A ⊗sB, s3A ⊗sB $s_{A}^{2} \otimes s_{B}, s_{A}^{3} \otimes s_{B}$ , and s1A ⊗sB $s_{A}^{1} \otimes s_{B}$ (or more precisely permute((s2A, ∑ j) $(s_{A}^{2}, \sum_{j})$ ) ⊗ permute(s_B, ∑_j), permute((s3A, ∑ j) $(s_{A}^{3}, \sum_{j})$ ) ⊗ permute(s_B, ∑_j) and permute ((s1A, ∑ j) $(s_{A}^{1}, \sum_{j})$ ) ⊗ permute(s_B, ∑_j)) resconstruct (p1)2j,(p2)2j ${(p_{1})}_{j}^{2}, {(p_{2})}_{j}^{2}$ and (p3)2j ${(p_{3})}_{j}^{2}$ , respectively. Table 3.6 is designed for this principle.

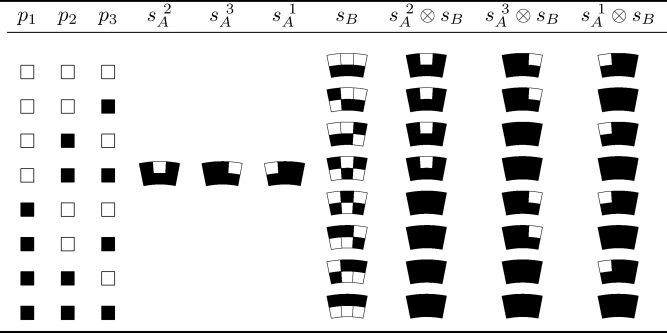
Images

Table 3_6 Encoding a set of corresponding pixels (p1,p2,p3)2j ${(p_{1}, p_{2}, p_{3})}_{j}^{2}$ into a2j $a_{j}^{2}$ (a3j $a_{j}^{3}$ and a1j $a_{j}^{1}$ ) and b2j $b_{j}^{2}$ in terms of s2A(s3A,s1A,respectively) $s_{A}^{2} (s_{A}^{3}, s_{A}^{1}, respectively)$ and s_B in the first chords of A and B, respectively for visual 3-secret sharing.

In fact, we can rearrange Table 3.6 to make the columns 4–10 exactly the same as those in Table 3.5. Table 3.7 is such a consequence. Note that Tables 3.5 and 3.7 are the same except for the headings of columns 1-3. From Table 3.7, we observe that given a set of corresponding pixels (p1,p2,p3)2j ${(p_{1}, p_{2}, p_{3})}_{j}^{2}$ , the elementary block of b2j $b_{j}^{2}$ can be easily determined by sbtod(p3,p1,p2)B $s_{B}^{b t o d (p_{3}, p_{1}, p_{2})}$ .

Following the above example shown in Figure 3.11, we have (p1,p2,p3)21=(■,■,□) ${(p_{1}, p_{2}, p_{3})}_{1}^{2} = (■, ■, □)$ and ∑₁ = (1, 2, 3,4, 5, 6, ). Since btod(p₃p₁p₂) = btod(011) = 3 b21 $b_{1}^{2}$ is encoded as permute (s3B, ∑ 1) $(s_{B}^{3}, \sum_{1})$ as show in Figure 3.13. It is easily seen that

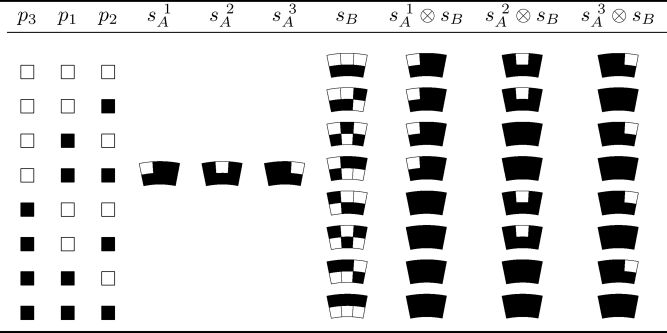
Images

Table 3_7 Encoding scheme equivalent to Table 6 for the second chords of A and B for visual 3-secret sharing.

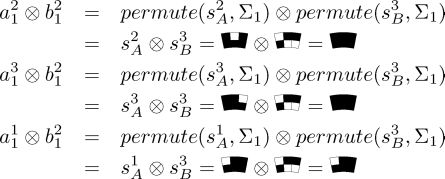
Images

FIGURE 3.13
Encoding b21 $b_{1}^{2}$ in B.

That is, a21 ⊗b21,a31 ⊗b21 $a_{1}^{2} \otimes b_{1}^{2}, a_{1}^{3} \otimes b_{1}^{2}$ , and a11 ⊗b21 $a_{1}^{1} \otimes b_{1}^{2}$ (the first blocks in the second chords of A ⊗ B, A¹²⁰° ⊗ B, and A²⁴⁰° ⊗ B) reconstruct (p1)21(■), (p2)21(■) ${(p_{1})}_{1}^{2} (■), {(p_{2})}_{1}^{2} (■)$ , and (p3)21(□) ${(p_{3})}_{1}^{2} (□)$ , respectively.

Based upon the experience above, Table 3.8 summarizes the encoding scheme for the blocks in the third chord of B for sharing 3 secrets. We can see from Table 3.8 that given a set of corresponding pixels (p1,p2,p3)3j ${(p_{1}, p_{2}, p_{3})}_{j}^{3}$ , the elementary block of b3j $b_{j}^{3}$ is chosen to be sbtod(p3,p1,p2)B $s_{B}^{b t o d (p_{3}, p_{1}, p_{2})}$ .

Images

Table 3_8 Encoding a set of corresponding pixels (p1,p2,p3)3j ${(p_{1}, p_{2}, p_{3})}_{j}^{3}$ into a3j (a1j and a2j) $a_{j}^{3} (a_{j}^{1} and a_{j}^{2})$ and b3j $b_{j}^{3}$ in terms of s3A $s_{A}^{3}$ (s1A,s2A $s_{A}^{1}, s_{A}^{2}$ , respectively) and s_B in the first chords of A and B, respectively for visual 3-secret sharing.

Following the previous example in Figure 3.11, consider the particular case (p1,p2,p3)31=(□,■,■) ${(p_{1}, p_{2}, p_{3})}_{1}^{3} = (□, ■, ■)$ . Since btod(p₂p₃p₁) = btod(110) = 6, we encode b31 $b_{1}^{3}$ as permute (s6B, ∑ 1) $(s_{B}^{6}, \sum_{1})$ as show in Figure 3.14. It is clearly seen that

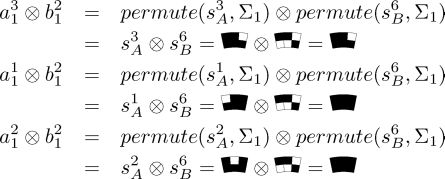
Images

We have that a31 ⊗b31,a11 ⊗b31 $a_{1}^{3} \otimes b_{1}^{3}, a_{1}^{1} \otimes b_{1}^{3}$ , and a21 ⊗b31 $a_{1}^{2} \otimes b_{1}^{3}$ (the first blocks in the third chords of A ⊗ B, A¹²⁰° ⊗ B, and A²⁴⁰° ⊗ B) recover (p1)31(□), (p2)31(■) ${(p_{1})}_{1}^{3} (□), {(p_{2})}_{1}^{3} (■)$ , and (p3)31(■) ${(p_{3})}_{1}^{3} (■)$ , respectively.

Figure 3.15 depicts the results of the first three blocks in the three chords of A ⊗ B, A¹²⁰° ⊗ B and A²⁴⁰° ⊗ B, which reconstruct (p1)k1 ${(p_{1})}_{1}^{k}$ in P₁ (□, ■, □) (Figure 3.15(a) vs. Figure 3.11(a)), (p2)k1 ${(p_{2})}_{1}^{k}$ in P₂ (■, ■, ■) (Figure 3.15(b) vs. Figure 3.11(b)) and b31 $b_{1}^{3}$ in P₃ (□, □, ■) (Figure 3.15(c) vs. Figure 3.11(c)), respectively for 1 ≤ k ≤ 3.

Images

FIGURE 3.14
Encoding (p3)k1 ${(p_{3})}_{1}^{k}$ in B.

Images

FIGURE 3.15
Results of (a) A ⊗ B, (b) A¹²⁰° ⊗ B, and (c) A²⁴⁰° ⊗ B.

Based upon the above discussions, we obtain bkj=permute(slB,∑j) $b_{j}^{k} = p e r m u t e (s_{B}^{l}, \sum_{j})$ where

l = ⎧ ⎩ ⎨ ⎪ ⎪ b t o d (p 1 p 2 p 3) b t o d (p 3 p 1 p 2) b t o d (p 2 p 3 p 1) if k=1; if k=2; otherwise,

$l = {\begin{array}{l} b t o d (p_{1} p_{2} p_{3}) & if k=1; \\ b t o d (p_{3} p_{1} p_{2}) & if k=2; \\ b t o d (p_{2} p_{3} p_{1}) & otherwise, \end{array}$

for the given set of corresponding pixels (p1,p2,p3)kj ${(p_{1}, p_{2}, p_{3})}_{j}^{k}$ with respect to pixel j of strip k in (P₁, P₂, P₃) where 1 ≤ j ≤ β and 1 ≤ k ≤ 3.

Let rotate(r₁r₂ … r_x, d) denote a function that rotates r₁r₂ … r_x right d bits where r_i ∈ {0, 1}, 1 ≤ i ≤ x and 0 ≤ d ≤ x − 1; that is,

r o t a t e (r 1 r 2 \dots r x, d) = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ r 1 r 2 \dots r x if d = 0; r x - d + 1 r x - d + 2 \dots r x r 1 r 2 \dots r x - d otherwise (1 \leq d \leq x - 1) . (3.3)

$r o t a t e (r_{1} r_{2} \dots r_{x}, d) = {\begin{array}{l} r_{1} r_{2} \dots r_{x} \\ if d = 0; \\ r_{x - d + 1} r_{x - d + 2} \dots r_{x} r_{1} r_{2} \dots r_{x - d} \\ otherwise (1 \leq d \leq x - 1) . \end{array} (3.3)$

Then the above formula can be simplified as

b k j = p e r m u t e (s b t o d (r o t a t e (p 1 p 2 p 3, k - 1)) B, Σ j) (3.4)

$b_{j}^{k} = p e r m u t e (s_{B}^{b t o d (r o t a t e (p_{1} p_{2} p_{3}, k - 1))}, Σ_{j}) (3.4)$

with respect to the set of corresponding pixels (p1,p2,p3)kj ${(p_{1}, p_{2}, p_{3})}_{j}^{k}$ where 1 ≤ j ≤ β and 1 ≤ k ≤ 3.

Since the number of subpixels in both of the elementary blocks of A and B is 6(= 2x) in the above case, the pixel expansion (i.e., the number of subpixels in the shares needed to encode a set of corresponding pixels in the secret images) in this algorithm is 6 for x = 3. The visual x-secret sharing scheme for any general number x ≥ 2 will be formalized in the following section.

3.4.1.4 General Algorithm

The definitions of the elementary blocks for circle shares A (formula (3.1)) and B (formula (3.4)) and the encoding scheme in Tables 3.5, 3.7, and 3.8 for visual 3-secret sharing can be generalized to accomplish the visual multisecret sharing for x ≥ 1 (including x =1) secrets. Furthermore, there is no need to store any codebook like Tables 3.5, 3.7, and 3.8. Thus, this scheme formally presented in the following is not only general but also efficient for physical implementation.

Assume that there are x secrets to be shared by two participants. The two circle shares A and B are evenly decomposed into x chords, respectively. Let θ denote the degree expanded in each chord of A and B. It is computed as

θ = 360 ° / x .

$θ = 360 ° / x .$

We refer to the elementary block of the x secrets as a block with 2x ordered subpixels as shown in Figure 3.16. It is noted that the pixel expansion in the scheme is 2x when x secrets are shared. The width and height of the elementary block can be any combination as long as their multiplication is 2x (or even any number larger than 2x for some special purposes, such as retaining aspect ratios, to ease the production of the circle shares, and so on). The order of the 2x subpixels in the elementary block can also be arbitrarily defined. In the following discussions, we follow the shape and order of the elementary block as shown in Figure 3.16.

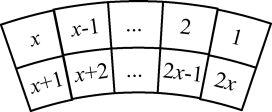
Images

FIGURE 3.16
Elementary block for x secrets.

We define the set of the elementary blocks for share A as follows:

E x A = {s k A ∣ ∣ 1 \leq k \leq x},

$E_{A}^{x} = {s_{A}^{k} | 1 \leq k \leq x},$

where skA $s_{A}^{k}$ is an elementary block consisting of one white and 2x − 1 black subpixels in which the jth subpixel, denoted as skA[j] $s_{A}^{k} [j]$ , is defined by

s k A [j] = {01 if j = x + 1 - k; otherwise, (3.5)

$s_{A}^{k} [j] = {\begin{array}{l} 0 & if j = x + 1 - k; \\ 1 & otherwise, \end{array} (3.5)$

for 1 ≤ j ≤ 2x and 1 ≤ k ≤ x.

Figure 3.17 shows the elementary blocks of A for encoding x = 4 secrets. As an example, we show how the subpixels in s2A $s_{A}^{2}$ are computed by formula (3.5). Since k = 2 and x + 1 − k = 4 + 1 − 2 = 3, thus skA[3]=0 $s_{A}^{k} [3] = 0$ and skA[j′]=1 $s_{A}^{k} [j^{'}] = 1$ for 1 ≤ j′ ≠ 3 ≤ 8(= 2x) as shown in Figure 3.17(b).

FIGURE 3.17
Elementary blocks in E4A $E_{A}^{4}$ : (a) s1A $s_{A}^{1}$ , (b) s2A $s_{A}^{2}$ , (c) s3A $s_{A}^{3}$ , (d) s4A $s_{A}^{4}$ .

We define the set of the elementary blocks for share B as follows:

E x B = {s γ B ∣ ∣ 0 \leq γ \leq 2 x - 1},

$E_{B}^{x} = {s_{B}^{γ} | 0 \leq γ \leq 2^{x} - 1},$

where sγB $s_{B}^{γ}$ is also an elementary block containing x white and x black subpixels in which the jth subpixel, denoted as sγB[j] $s_{B}^{γ} [j]$ , is defined by

s γ B [j] = {r j r ¯ 2 x + 1 - j 1 \leq j \leq x; otherwise, (3.6)

$s_{B}^{γ} [j] = {\begin{array}{l} r_{j} & 1 \leq j \leq x; \\ {\bar{r}}_{2 x + 1 - j} & otherwise, \end{array} (3.6)$

where γ = btod(r_xr_x−1 … r₂r₁), r_t is the tth least significant bit of γ is represented in binary (x-bit) in which 1 ≤ t ≤ x and 0 ≤ γ ≤ 2^x − 1 for 1 ≤ j ≤ 2x and r¯t ${\bar{r}}_{t}$ is the inverse of r_t.

Figure 3.18 illustrates the elementary blocks of B for x = 4. Consider s4B $s_{B}^{4}$ . Since γ = 4 = btod(r₄r₃r₂r₁) = btod(0100)₂, we have (s4B[1],s4B[2],s4B[3],s4B[4])=(r1,r2,r3,r4,)=(0,0,1,0) $\begin{matrix} (s_{B}^{4} [1], s_{B}^{4} [2], s_{B}^{4} [3], s_{B}^{4} [4]) & = (r_{1}, r_{2}, r_{3}, r_{4},) & = (0, 0, 1, 0) \end{matrix}$ and (s4B[5],s4B[6],s4B[7],s4B[8])=(r¯2×4+1−5,r¯2×4+1−6,r¯2×4+1−7,r¯2×4+1−8)=(r¯4,r¯3,r¯2,r¯1)=(1,0,1,1) $(s_{B}^{4} [5], s_{B}^{4} [6], s_{B}^{4} [7], s_{B}^{4} [8]) = ({\bar{r}}_{2 \times 4 + 1 - 5}, {\bar{r}}_{2 \times 4 + 1 - 6}, {\bar{r}}_{2 \times 4 + 1 - 7}, {\bar{r}}_{2 \times 4 + 1 - 8}) = ({\bar{r}}_{4}, {\bar{r}}_{3}, {\bar{r}}_{2}, {\bar{r}}_{1}) = (1, 0, 1, 1)$ . Thus, s4B $s_{B}^{4}$ is as shown in Figure 3.18(e).

Formulae (3.1) and (3.4) about the encoding of blocks in A and B, respectively, for x = 3 can now be formulated in a more generalized form as follows. The blocks in A are encoded by

(a 1 j, a 2 j, \dots, a x j) = (p e r m u t e (s 1 A, Σ j), p e r m u t e (s 2 A, Σ j), \dots, p e r m u t e (s x A, Σ j)), (3.7)

$(a_{j}^{1}, a_{j}^{2}, \dots, a_{j}^{x}) = (p e r m u t e (s_{A}^{1}, Σ_{j}), p e r m u t e (s_{A}^{2}, Σ_{j}), \dots, p e r m u t e (s_{A}^{x}, Σ_{j})), (3.7)$

where ∑_j is a random permutation of {1, 2, . . . , 2x} for 1 ≤ j ≤ β.

Given a set of corresponding pixels (p1,p2,…,px)kj ${(p_{1}, p_{2}, \dots, p_{x})}_{j}^{k}$ in block j of strip k in (P1,P2,…,Px),bkj $(P_{1}, P_{2}, \dots, P_{x}), b_{j}^{k}$ (i.e., block j of chord k in B) is encoded by

b k j = p e r m u t e (s b t o d (r o t a t e (p 1 p 2 \dots p x, k - 1)) B, Σ j) (3.8)

$b_{j}^{k} = p e r m u t e (s_{B}^{b t o d (r o t a t e (p_{1} p_{2} \dots p_{x}, k - 1))}, Σ_{j}) (3.8)$

Images

FIGURE 82.3
Elementary blocks in E4B:(a)s0B,(b)s1B,(c)s2B,(d)s3B,(e)s4B,(f)s5B,(g)s6B,(h)s7B,(i)s8B,(j)s9B,(k)s10B,(l)s11B,(m)s12B,(n)s13B,(i)s14B,(i)s15B $E_{B}^{4} : (a) s_{B}^{0}, (b) s_{B}^{1}, (c) s_{B}^{2}, (d) s_{B}^{3}, (e) s_{B}^{4}, (f) s_{B}^{5}, (g) s_{B}^{6}, (h) s_{B}^{7}, (i) s_{B}^{8}, (j) s_{B}^{9}, (k) s_{B}^{10}, (l) s_{B}^{11}, (m) s_{B}^{12}, (n) s_{B}^{13}, (i) s_{B}^{14}, (i) s_{B}^{15}$ .

for 1 ≤ j ≤ β and 1 ≤ k ≤ x where function ratote(p₁p₂ ….p_x, k − 1) is defined by formula (3.3).

Based upon the above definitions and formulae (3.5)–(3.8), our visual multi-secrets sharing scheme is formally presented in Algorithm 1.

Algorithm 1. Encoding x secret images into two circle shares

Input: x h × w binary secret image P₁, P₂, …, P_x

Output: two circle shares A and B such that any single A or B leaks no information about any one of the secret images, while A^(j−1)θ ⊗ B recovers P_i for 1 ≤ i ≤ x in the human visual system where θ = 360°/x and A⁰°

1. Create A and B as circle shares, which are decomposed into x chords where each chord is composed by β = h× (w/x) chord-shaped blocks referred to as akj $a_{j}^{k}$ and bkj $b_{j}^{k}$ , 1 ≤ k ≤ x and 1 ≤ j ≤ β, respectively and each block contains 2x subpixels.

2. Generate ExA $E_{A}^{x}$ and ExB $E_{B}^{x}$ according to formulae (5) and (6), respectively.

3. for (each block j, 1 ≤ j ≤ β) do

3.1 { Determine ∑_j = (σ₁, σ₂, …, σ_2x), a random permutation of {1, 2, …, 2x}

3.2 for (each chord k, 1 ≤ k ≤ x) do

{ //all β blocks in x chords of A and B adopt the same permutation ∑_j

3.2.1 akj=permute(skA,∑j) $a_{j}^{k} = p e r m u t e (s_{A}^{k}, \sum_{j})$

3.2.2 for (each secret image i, 1 ≤ i ≤ x) do qi=(pi)kj $q_{i} = {(p_{i})}_{j}^{k}$

3.2.3 γ = btod(rotate(q₁q₂ … q_x, k − 1))

3.2.4 bkj=permute(sγB,∑j) $b_{j}^{k} = p e r m u t e (s_{B}^{γ}, \sum_{j})$ }

4. output(A, B) // A and B are composed by all ak,jS $a_{j}^{k,} S$ and bk,jS $b_{j}^{k,} S$ , respectively

Note that a new permutation ∑_j is determined to permute the subpixels in each pair of akj $a_{j}^{k}$ and bkj $b_{j}^{k}$ for 1 ≤ k ≤ x to ensure the entire randomness that the subpixels in akj $a_{j}^{k}$ and bkj $b_{j}^{k}$ can provide. Further, akj $a_{j}^{k}$ and bkj $b_{j}^{k}$ are encoded by using the same permutation ∑_j so that the numbers of the white and black subpixels in akj⊗bkj $a_{j}^{k} \otimes b_{j}^{k}$ and skA⊗bγB $s_{A}^{k} \otimes b_{B}^{γ}$ are exactly the same for 1 ≤ k ≤ x.

The pixel expansion of Shyu et al.’s scheme is 2x when x secrets are shared. In the case of x = 2, the pixel expansion is 2x = 4 which is the same as that of Wu and Chen [12] as well as Wu and Chang [13]. The number of all possible patterns in an extended block in S₁ [12] (see Figure 3.2(c)) or any sector block in A [13] (see Figure 3.4(a)) is 4, which contains two white and two black subpixels, while that in bkj $b_{j}^{k}$ of the scheme is (4!)/(2! × 2!) = 6. The randomness of this scheme, in the case of x = 2, is surely better than that of Wu and Chen as well as Wu and Chang.

It is seen from Algorithm 1 that we do not physically store any information about Tables 3.5, 3.7, and 3.8 in memory. The elementary blocks Sk,AS $S_{A}^{k,} S$ and Sγ,BS $S_{B}^{γ,} S$ are generated in the run time (Step 2 in Algorithm 1) according to formulae (3.5) and (3.6). The encoding process is guaranteed by formulae (3.7) and (3.8) (Step 3 in Algorithm 1).

3.4.2 Feng et al.’s Scheme

Regarding Feng et al.’s (2, 2, x) scheme [3], x secret images P₁, P₂, …, P_x are encoded into two shares A and B. Each set of x corresponding pixels (in x secret images) is encoded into two blocks, namely s_A ∈ A and s_B ∈ B, each of which consists of x rows containing 3 pixels each. The pixel expansion is thus 3x. The rotation relationship for revealing each of the x secrets is similar to Shyu et al.’s scheme where the ith secret is revealed by A ⊗ B^(i−1)θ for 1 ≤ i ≤ x. One special design in their scheme is that the encoded shares are in the form of cylinders to avoid the distortion of the revealed secrets.

They chose four types of 3-pixel patterns, referred to as the effective block ineffective block white block and black block to construct S_A and s_B. It is evident that and .

Figure 3.19 specifically illustrated the stacked results of these chosen patterns in their scheme.

Images

FIGURE 84.3
Stacking results of the chosen visual patterns for Feng et al.’s scheme.

Table 3.9 lists a possible set of encoded patterns for s1A,s2A,s3A, $s_{A}^{1}, s_{A}^{2}, s_{A}^{3},$ , and s_B; and their stacked results for x = 3. The reason that p_i is reconstructed by siA⊗sB $s_{A}^{i} \otimes s^{B}$ is precisely explained in this table. Surely, each set of the encoded pattern could be permuted correspondingly to accomplish the randomness for the whole shares.

Images

Table 3_9 Possible set of encoded patterns for s1A,s2A,s3A, $s_{A}^{1}, s_{A}^{2}, s_{A}^{3},$ , and s_B; and their stacked results for x = 3.

3.4.3 Experimental Results

Here, we implement Shyu et al.’s visual multisecret sharing scheme due to its generality on the abstraction and the superiority on the pixel expansion (over Feng et al.’s scheme).

We coded the program by using Borland C++ Builder (BCB) in a personal computer running MS Windows. Since the blocks are in the shape of chords, we called the embedded functions in BCB such as circle drawing, line drawing, flood-filling a closed area, and so on, to build the chord-shaped blocks in the scheme.

Four experiments were designed to explore the feasibility and applicability of the visual multisecret sharing scheme. Experiment 1 verifies the correctness of the scheme for x = 3 where the starting position for encoding on the circle shares are fixed as above-mentioned. Experiment 2 demonstrates that the scheme can be easily extended in such a way that the starting position for encoding can be arbitrarily assigned. This increases the secrecy of the proposed scheme. Experiment 3 gives the implementation results of the visual 4-secret sharing scheme. Experiment 4 presents implementation results of encoding the shares using cylinder (instead of circle) shares.

Experiment 1: Figure 3.20 illustrates the results of a computer implementation of the proposed scheme for sharing three secret images. Figures 3.20(a)–(c) are the three secrets to be shared, namely P₁, P₂, and P₃, respectively. Figures 3.20(d) and (e) show the circle shares A and B encoded by Algorithm 1, which expose no information about P₁ , P₂ , and P₃ individually. Figures 3.20(f)–(h) reveal the superimposed results of A ⊗ B, A¹²⁰ ⊗ B°, and A²⁴⁰° ⊗ B, which reconstruct P₁, P₂, and P₃ in our visual system, respectively. Figure 3.20(i) gives another superimposed result, A⁸⁵° ⊗ B that leaks no information about any of the three secrets. In fact, any result of A^θ ⊗ B, for θ = 0 , 120°, 240°, is merely a seemingly random picture.

Experiment 2: The encoding processes of A and B in the algorithm start from the 0 position and move on in a clockwise direction (see Figure 3.5). However, the starting position for encoding in A (or B) can be predefined arbitrarily.

Figure 3.21 shows the implementation results of using the same example as in Experiment 1 with a different starting starting position in B; that is, we encoded B by starting from the 85 position (85 counterclockwise to the 0 position) while we encoded A by starting from the 0 position as mentioned. The three secret images are the same as those in Figures 3.20(a)–(c). Figures 3.21(a) and (b) are the circle shares A′ and B′ encoded by Algorithm 1. Figure 3.21(c) shows the result of A′ ⊗ B′, which reveals nothing about the secrets, while Figures 3.21(d)–(f) display the superimposed results of (A′)⁸⁵° ⊗ B′, (A′)²⁰⁵° ⊗ B′ and (A′)³²⁵° ⊗ B′ that reconstruct P₁, P₂, and P₃, respectively, in our visual system. Note that both A ⊗ B (Figure 3.20(f)) and (A′)⁸⁵ ⊗ B′ is 85 counterclockwise away from that in A ⊗ B.

Images

FIGURE 86.3
Implementation results for the proposed visual 3-secret sharing scheme: (a) P₁, (b) P₂, (c) P₃,(d) A, (e) B, (f) A ⊗ B, (g) A¹²⁰° ⊗ B, (h) A²⁴⁰° ⊗ B, (i) A⁸⁵° ⊗ B.

Experiment 3: Figure 3.22 gives the implementation results of the proposed scheme for sharing four secrets. Figures 3.22(a)–(d) are the four secrets to be shared, namely P₁, P₂, P₃, and P₄, respectively. Figures 3.22(e) and (f) are the encoded circle shares A and B. Figures 3.22(g)–(j) show the superimposed results of A ⊗ B, A⁹⁰° ⊗ B, A¹⁸⁰° ⊗ B, and A²⁷⁰° ⊗ B that recover P₁, P₂, P₃, and P₄ in our visual system, respectively.

Experiment 4: One disadvantage in applying circle shares is that the reconstructed secrets might be distorted. This shortcoming could be easily refined by introducing cylinder shares.

Suppose that we encode each set of x pixels into square blocks (instead of chord blocks) in Shyu et al.’s scheme. The encoded shares evolve into the shape of rectangles. Each of the two rectangle shares can be easily rolled up into a cylinder by aligning the rightmost column next to the leftmost one. Figure 3.23 shows an example of applying cylinder shares to reveal the corresponding distorted secrets where (a) and (b) are distorted reconstructed secrets (which are the same as those in Figure 3.22(g) and (j), respectively) using circular shares, while (c) and (d) are the corresponding counterparts using cylinder shares which avoid any distortion when exposing the secrets.

The results in Experiments 1–4, as expected, demonstrate the feasibility and applicability of Shyu et al.’s visual multisecret sharing scheme. We compare the performances of the aformentioned schemes in terms of the capability of sharing secrets, pixel expansion, contrast, and shape of shares in the next subsection.

3.4.4 Comparison and Discussions

When we deal with x secrets, the pixel expansion of Shyu et al.’s scheme [8] is 2x and the contrast (i.e., the relative difference between the reconstructed white and black pixels in the superimposed image) of the scheme is 1/(2x) since all 2x subpixels in a reconstructed black pixel are black, while those in a reconstructed white pixel are 2x. Suppose that Feng et al.’s scheme is applied. The pixel expansion becomes 3x and the contrast is 1/(3x). Note that when x = 2, the pixel expansions (contrasts) in Wu and Chen’s [12], Wu and Chang’s [13], and Shyu et al’s schemes are all 4 (1/4); while in Feng et al.’s scheme is 6 (1/6).

Table 3.10 summarizes the numbers of secrets shared (denoted as x), pixel expansions(denoted as m), contrasts, and the shapes of shares in these visual multiple-secret sharing schemes for the comparison purpose.

The pixel expansion of Shyu et al.’s scheme [8] is 2x when x secrets are shared. It would be challenging to prove whether or not it is optimal. Is there any algorithm that improves the contrast in the scheme? It is surely worthy of further study. How to extend Shyu et al.’s scheme such that multiple secrets can be shared by more than two shares is also an interesting topic. Potentially, sharing multiple secrets may have more flexibilities and applications than sharing only one secret. Visual identification and visual authentication are some typical applications in visual cryptography [6]. It would be of much significance to reexamine these topics from a viewpoint of sharing multiple secrets.

Images

FIGURE 88.3
Implementation results for the proposed visual 3-secret sharing scheme with a different starting encoding position: (a) A′, (b) B′, (c) A′ ⊗ B′, (d) (A′)⁸⁵° ⊗ B′, (e) (A′)²⁰⁵° ⊗ B′, (f) (A′)³²⁵° ⊗ B′.

Images

FIGURE 89.3
Results of computer implementation for 4-secret sharing: (a) P₁, (b) P₂, (c) P₃, (d) P₄, (e) A, (f) B, (g) A ⊗ B, (h) A⁹⁰° ⊗ B, (i) A¹⁸⁰° ⊗ B (j) A²⁷⁰° ⊗ B.

Images

FIGURE 90.3
Transforming circle shares (a) and (b) into cylinder counterparts (c) and (d), respectively.

Table 3.10 Comparison of visual multiple secrets sharing schemes.

Schemes	x	m	contrast	shares’ shape
Wu and Chen [12]	2	4	1/4	square
Wu and Chang [13]	2	4	1/4	square
Feng et al.[3]	≥2	3x	1/3x	cylnder
Shyu et al.[8]	≥2	2x	1/2x	circle or cylinder

As a matter of fact, the sharing of multiple secrets visually brings forth new problems to be considered. For instance, with regard to the “starting position for encoding” in A or/and B in Experiment 2, we may design such a concern to be some kind of private key, which is only accessible between the dealer and authorized participant(s). Without the correct starting positions in A or/and B, the alignment of A and B cannot recover the secret yet. In addition, the second secret of the three secrets in Experiment 1 might be designed to be fake for the purpose of diffusion. That is to say whether the whole secret message is “Help is never on its way"or “Help is on its way” may be treated to be another private key between the dealer and authorized participant(s). Mainly, the number of secrets, the degree of the starting position for encoding, the combination of the true or fake reconstructed secrets, and so on, can be designed as private keys to increase the level of security in the visual multi-secret sharing system.

3.5 Concluding Remarks

By adopting circle or cylinder shares, we discuss general visual secret sharing schemes for x ≥ 1 (indeed, these schemes work well for x = 1) secrets in two shares in this chapter. The previous studies considered sharing only two secrets in two shares [12, 13]. Shyu et al.’s scheme can be implemented easily and it takes only some constant working space. All encoding information can be determined in run time. By introducing an independent random permutation (i.e., ∑_j, see formulae (3.1) and (3.4)) when encoding each pair of the corresponding blocks (i.e., akj $a_{j}^{k}$ and bkj $b_{j}^{k}$ , see Step 3.2.1 and 3.2.4 in Algorithm 1), the scheme ensures the maximum randomness that the subpixels in an encoded block may possibly provide. For the transmitter, one machine capable of running the encoding scheme is needed, while for the receivers, no computing device is required and the decryption process is simply by the human visual system. The proposed scheme can be easily extended to gray-level images by adopting the halftone technology [4] or even color images by exploiting color decomposition [4] or color composition [9].

In traditional visual secret-sharing schemes, rectangle shares are encoded to conceal one shared secret. They are easily superimposed by aligning the rectangular corners. As compared to the rectangle shares, the circle or cylinder shares are relatively hard to superimpose since there are no reference points to align with. Basically, the usage of the circle or cylinder shares increases the complexity in decoding the secrets. In practical applications, the dealer might add additional information in the circle shares, such as some supplementary points, lines, or markers, to ease the superimposition (decoding process) for the participants. Figure 3.24 shows one possible arrangement in the case of sharing three secrets as in Experiment 1. Note that circle share A has three markers (see Figure 3.24(a)), while B has only one (see Figure 3.24(b)) based upon which A, A^120° , and A^240° can be superimposed with B easily. Or, the dealer can deliberately organize such information as private key(s) such that only the legal receivers are informed how to obtain the key(s). The same reasoning could be applied if the cylinder shares are adopted.

Images

FIGURE 3.24
Shares (based upon Experiment 1) with supplementary lines to ease the alignments: (a) A with three markers, (b) B with one marker.

Generally speaking, the use of circle or cylinder shares to convey several secrets discloses some new issues that have not yet been considered in traditional visual cryptography, such as “How many secrets are there?,”“How to superimpose the shares (where to align with or in what rotation angles)?,”“Is there any fake secret(s) for diffusion?,”and so on. These concerns can be designed as a set of private keys. The consideration and distribution of these private keys can be further discussed.

Bibliography

[1] G. Ateniese, C. Blundo, A. De Santis, and D.R. Stinson. Visual cryptography for general access structures. Inf. Comput., 129:86–106, 1996.

[2] C. Blundo, A. De Santis, and D.R. Stinson. On the contrast in visual cryptography schemes. J. Cryptogr., 12:261–289, 1999.

[3] J. B. Feng, H. C. Wu, C. S. Tsai, Y. F. Chang, and Y. P. Chu. Visual secret sharing for multiple secrets. Pattern Recognition, 41:3572–3581, 2008.

[4] Y.C. Hou. Visual cryptography for color images. Pattern Recognition, 36:1619–1629, 2003.

[5] C.C. Lin and W.H. Tsai. Visual cryptography for grey-level images by dithering techniques. Pattern Recognition Lett., 24:349–358, 2003.

[6] M. Naor and B. Pinkas. Visual authentication and identification. in: B.S. KaliskiJr. (Ed.), Advances in Cryptology: CRYPTO97, Lecture Notes in Computer Science, 1294:322–336, 1997.

[7] M. Naor and A. Shamir. Visual cryptography. in: A. De Santis (Ed.), Advances in Cryptology: Eurpocrypt'94, Lecture Notes in Computer Science, 950:1–12, 1995.

[8] S. J. Shyu, S.Y. Huang, Y.K. Lee, R.Z. Wang, and K. Chen. Sharing multiple secrets in visual cryptography. Pattern Recognition, 40:3633–3651, 2007.

[9] S.J. Shyu. Efficient visual secret sharing scheme for color images. Pattern Recognition, 39:866–880, 2006.

[10] D.R. Stinson. An introduction to visual cryptography. Public Key Solution ’97, pages 20–30, April 1997.

[11] E.R. Verheul and H.C.A. Van Tilborg. Constructions and properties of k out of n visual secret sharing schemes. Designs Codes Cryptography, 11:179–196, 1997.

[12] C.C. Wu and L.H. Chen. A study on visual cryptography, Master Thesis. PhD thesis, Institute of Computer and Information Science, National Chiao Tung University, Taiwan, R.O.C., 1998.

[13] H.C. Wu and C.C. Chang. Sharing visual multi-secrets using circle shares. Comput. Stand. Interfaces, 134((28):123–135, 2005.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for
3 Visual Cryptography for Multiple Secrets

3

Visual Cryptography for Multiple Secrets

CONTENTS

3.1 Introduction

3.2 Naor and Shamir’s Basic Visual Secret Sharing Scheme

3.3 Visual Two-Secret Sharing Schemes

3.3.1 Wu and Chen’s Scheme

3.3.2 Wu and Chang’s Scheme

3.4 Visual Multiple-Secret Sharing Schemes

3.4.1 Shyu et al.’s Scheme

3.4.1.1 Informal Description

3.4.1.2 Encoding Circle Share A

3.4.1.3 Encoding Circle Share B

3.4.1.4 General Algorithm

3.4.2 Feng et al.’s Scheme

3.4.3 Experimental Results

3.4.4 Comparison and Discussions

3.5 Concluding Remarks

Bibliography

Table of Contents for 3 Visual Cryptography for Multiple Secrets

Create new playlist

Sign In

Sign Up

CONTENTS

Table of Contents for
3 Visual Cryptography for Multiple Secrets