9 Visual Cryptography Schemes with Reversing

A visual cryptography scheme for a set of n participants is a method to encode a secret image, consisting of black and white pixels, into n shadow images called shares, one for each participant. Each share is a collection of black and white subpixels, which are printed in close proximity to each other, so that the human visual system averages their individual black/white contributions. The encoding is done in such a way that certain subsets of participants, called qualified sets, can ”visually” recover the secret image, but other subsets of participants, called forbidden sets, cannot gain any information (in an information-theoretic sense) about the secret image by inspecting their shares. A ”visual” recover for a set of qualified participants consists of xeroxing each share onto a separate transparency, of stacking together the transparencies and projecting the result with an overhead projector. If the transparencies are aligned carefully, then the participants will be able to see the secret image (without any knowledge of cryptography and without performing any cryptographic computation).

This cryptographic paradigm was introduced by Naor and Shamir [11]. They analyzed the case of (k, n)-threshold visual cryptography schemes, in which the qualified subsets of participants have cardinality k, whereas, the forbidden subsets of participants have cardinality less than k. Some results on (k, n)-threshold visual cryptography schemes ((k, n)-threshold visual cryptography scheme (VCS), for short) can be found in [1,2,5,8,10,12]. The model by Naor and Shamir has been extended in [1] to general access structures (an access structure is a specification of all qualified and forbidden subsets of participants), where general techniques to construct visual cryptography schemes for any access structure have been proposed.

Visual cryptography schemes are characterized by two parameters: The pixel expansion, corresponding to the number of subpixels contained in each share (transparency) and the contrast, which measures the ”difference” between a black and a white pixel in the reconstructed image. Visual cryptography schemes such that, in the reconstructed image, all the subpixels associated to a black pixel are black, are referred to as visual cryptography schemes with perfect reconstruction of black pixels. Such schemes have been considered in [12,4,3]. Unfortunately, it is not possible to obtain visual cryptography schemes with perfect reconstruction of both black and white pixels. Such schemes are said to have ideal contrast.

In order to obtain perfect black visual cryptography schemes whose reconstruction of white pixels is almost perfect, Viet and Kurosawa [13] proposed a different kind of VCS, called VCS with reversing. Such VCSs require the introduction of an extra noncryptographic operation, that participants can use to reconstruct the image. Such an operation, which can be easily performed by many copy machines, is applied to a transparency and creates another transparency in which black pixels are reversed to white pixels and vice versa.

Specifically, Viet and Kurosawa [13] proposed to run c times (with c arbitrary constant) the distribution phase of a VCS with perfect reconstruction of black pixels and pixel expansion m, hence requiring each participant to store c•m subpixels for each pixel of the original image. The larger the number of runs c, the better the contrast of the resulting VCS with reversing. The drawback of such a solution is that the number of pixels in the reconstructed image, which depends on both the number of runs and on the pixel expansion of the underlying VCS, is greater than that in the original secret image, i.e., there is a loss of resolution.

Subsequently, Cimato, De Santis, Ferrara, and Masucci [6] showed how to construct VCSs with reversing where reconstruction of both black and white pixels is perfect. In particular, Cimato et al. [6] proposed two different constructions. The first solution uses the fact that the introduction of the reversing operation, in addition to the stacking operation, allows participants to compute any Boolean function of their transparencies, since these two operations, corresponding to NOT and OR, respectively, represent a complete basis for Boolean functions. In particular, the construction uses a binary secret sharing scheme and requires each participant to hold r transparencies, where r denotes the size of the largest share in the underlying secret sharing scheme. The second solution uses as a building block a VCS with perfect reconstruction of black pixels, having a certain pixel expansion m and requires each participant to store m transparencies, each having the same number of pixels as the original image. Compared to the scheme of Viet and Kurosawa, such a scheme requires each participant to store m pixels instead than c-m, for each pixel of the original image, where c is the number of runs of the underlying VCS needed in [13] to obtain an asymptotically ideal contrast. By using a sequence of stacking and reversing operations on their transparencies, in both schemes proposed by Cimato et al. [6], each qualified set of participants recover the original secret image with no loss of resolution.

Later, Hu and Tzeng [9] considered the problem of reducing the number of the transparencies held by each participant in VCSs with reversing. They proposed a construction for ideal contrast VCSs with reversing requiring each participant to store only two transparencies. In particular, the first one contains an encoding of the secret image, whereas, the second one is an auxiliary transparency needed for the reconstruction phase. However, the size of each transparency is |Г₀| times larger than the size of the secret image, where |Г₀| denotes the minimum number of subsets qualified to reconstruct the secret image. Indeed, each transparency contains |Г₀| blocks and each qualified subset of participants reconstructs, without loss of resolution, the secret image in a single block, whereas the other reconstructed blocks contain only white pixels.

Then, Yang et al. [14] proposed two different constructions for ideal contrast VCS with reversing. In particular, one of their schemes removes the need of using as a building block a VCS with perfect reconstruction of black pixels. However, there is a loss of resolution in both their schemes.

Organization. In Section 9.2 we recall the definition and security requirements of VCSs. In Section 9.3 we describe the almost ideal contrast VCS with reversing by Viet and Kurosawa. In Section 9.4 we show and compare some ideal contrast VCSs with reversing that use as a building block any perfect black VCS. Finally, a VCS with reversing constructed upon any VCS is described in Section 9.4.3..

9.2 Visual Cryptography Schemes

Let P = {1,...,n} be a set of elements called participants, and let 2^P denote the set of all subsets of P. Let Г_Qual ⊆ 2^P and Г_Forb ⊆ 2^P, where Г_Qual ⋂ Г_Forb = θ. We refer to members of Г_Qual as qualified sets and we call members of Г_Forb forbidden sets. The pair (Г_Qual,Г_Forb) is called the access structure of the scheme. Define To to consist of all the minimal qualified sets: Г₀ = {X ∈ Г_Qual : X′ ∉ Г_Qua for all X′ ⊂ X}. In the case where Г_Qual is monotone increasing, Г_Forb is monotone decreasing, and Г_Qual⋃Г_Forb=2^P, the access structure is said to be strong. In a strong access structure, Г_Qual = {C ⊆ P : B ⊆ C for some B ∈ Γ₀}, and we say that Γ_Qual is the closure of Γ₀. A participant i ∈ P is an essential participant for (Γ_Qual,Г_Forb) if there exists a set X ⊆P such that X ⋃ {i} ∈ Г_Qual but X ∉ Г_Qual. If a participant is not essential then we can construct a visual cryptography scheme giving him nothing as his share. In fact, a nonessential participant does not need to participate actively in the reconstruction of the image, since the information he has is not needed by any set in P in order to recover the secret image. Therefore, unless otherwise specified, we assume throughout this chapter that all participants are essential.

The secret image consists of black and white¹ pixels. In order to share each pixel of the secret image the owner of the secret, usually called the dealer, provides each participant with a share (transparency), which is an enlarged version of the secret pixel consisting of a certain number m of subpixels, which are printed in close proximity to each other, so that the human visual system averages their individual black/white contributions. Notice that the term “subpixel” is misleading since a pixel is the smallest unit we can control on an image and thus we cannot further divide the pixel into subpixels. So the shared version of the original secret pixel will consist of m pixels, which are called subpixels because all together they represent the original secret pixel. The value m is called pixel expansion. The shares can be conveniently represented with an n × m matrix S where each row represents one share, i.e., m subpixels, and each element is either 0, for a white subpixel, or 1 for a black subpixel.

To reconstruct the secret image a group of participants stacks together their shares. The grey level of the combined share, obtained by stacking the transparencies i₁,..., i_s, is proportional to the Hamming weight w(V) of the m-vector V = OR $(r_{i_{1}}, \dots, r_{i_{s}})$ $(r_{i_{1}}, \dots, r_{i_{s}})$ , where $r_{i_{1}}, \dots, r_{i_{s}}$ $r_{i_{1}}, \dots, r_{i_{s}}$ are the rows of S associated with the transparencies we stack. This grey level is interpreted by the visual system of the users as black or as white in accordance with some rule of contrast. Since each secret pixel is represented by m pixels in the shares, the reconstructed image will be bigger than the original (depending on m and on the actual positions of the pixels, the image can also be distorted; a perfect square is a good choice for m because it avoids distortion). The characteristics of the model are encapsulated in the following definition, which is a generalization of the definition of (k, n)-threshold VCSs due to [12].

Definition 1 Let (Г_Qual, Г_Forb) be an access structure on a set of n participants. Two collections (multisets) of n × m Boolean matrices Co and C₁ con-stitute a visual cryptography scheme (Г_Qual, Г_Forb)-VCS with pixel expansion m if there exist two integers l and h such that h > l satisfying:

1. Any (qualified) set X − {i₁, i₂,..., i_p} ∈ Г_Qual can recover the shared image by stacking their transparencies.

Formally, for any M ∈ C₀, the ”or” V of rows i₁, i₂,..., i_p satisfies w_H (V) ≤ m − h; whereas, for any M ∈ C₁ it results that w_H(V) ≥ m − l.

2. Any (forbidden) set X − {i₁,i₂,..., i_p} ∈ Г_Forb has no information on the shared image.

Formally, the two collections of p × m matrices D_t, with t ∈ {0, 1}, obtained by restricting each n × m matrix in C_t to rows i₁, i₂,..., i_p are indistinguishable in the sense that they contain the same matrices with the same frequencies.

To share a white (black, resp.) pixel, the dealer randomly chooses one of the matrices in C₀ (C₁, resp.), and distributes row i to participant i. The chosen matrix defines the m subpixels in each of the n transparencies.

The first property of Definition 1 is related to the contrast of the image. It states that when a qualified set of participants stack their transparencies, they can correctly recover the image shared by the dealer. A pixel will be seen as a white pixel if sufficiently many subpixels (at least h) in the reconstructed image are white; whereas, it will be seen as a black one if not too many (at most l) are white. The value (h − l)/(h + l) is referred to as the contrast of the reconstructed image. Contrast gives a measurement of how clear the reconstructed image is in relation to the original one. The second property of Definition 1 is related to the security of the scheme, since it implies that, even by inspecting all their shares, any forbidden set of participants cannot gain any information in deciding whether the shared pixel was white or black.

Several visual cryptography schemes have been realized by using two n×m matrices, S⁰ and S¹, called basis matrices. The collections C₀ and C₁ are obtained by permuting the columns of the corresponding basis matrix (S⁰ for C₀, and S¹ for C₁ ) in all possible ways. This technique has been introduced in [11].

9.2.1 (k, k)-Threshold Visual Cryptography Schemes

In a (k, k)-threshold visual cryptography scheme the secret image is visible if and only if all k transparencies are stacked together, but totally invisible if fewer than k transparencies are stacked together or analyzed by any other method.

Naor and Shamir [11] proposed a construction for (k, k)-threshold VCSs using two basis matrices S⁰ and S¹ defined as follows: S⁰ is the matrix whose columns are all the Boolean k-vectors having an even number of 1’s, and S¹ is the matrix whose columns are all the Boolean k-vectors having an odd number of 1’s. The pixel expansion m of such a scheme is equal to 2^k−1 and the relative difference (h − l)/m between reconstructed white and reconstructed black is equal to 1/2^k−1. The above construction is optimal with respect to the pixel expansion and the relative difference between reconstructed white and reconstructed black.

Example 1 The basis matrices S⁰ and S¹ in a (4, 4)-threshold VCS are

s^{0} = [\begin{array}{l} 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 \end{array}] s^{1} = [\begin{array}{l} 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 & 1 & 1 & 0 \end{array}]

$s^{0} = [\begin{array}{l} 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 \end{array}] s^{1} = [\begin{array}{l} 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 & 1 & 1 & 0 \end{array}]$

The collections C₀ and C₁ are obtained by permuting the columns of the corresponding basis matrix (S⁰ for C₀, and S¹ for C₁) in all possible ways. In this scheme each pixel of the secret image is encoded into m − 8 subpixels.

It is easy to see that the integers h =1 and l = 0 satisfy Property 1 of Definition 1. Let S⁰ be the matrix chosen by the dealer to share a white pixel; by stacking the transparencies held by all four participants we get the vector (0,1,1,1, 1, 1,1,1, 1). On the other hand, let S¹ be the matrix chosen by the dealer to share a black pixel; by stacking the transparencies held by all four participants we get the vector (1, 1, 1, 1, 1, 1, 1, 1, 1). Property 2 of Definition 1 can also be easily verified. Indeed, consider what happens when less than four participants stack their together transparencies. For example, consider the first three participants and notice that, by stacking their shares, we get the vector (0, 1, 1, 1, 1, 1, 1, 1, 1) in both cases when the shared pixel is either white or black. Thus, the participants are not able to distinguish the color of the shared pixel by inspecting their shares.

9.2.2 Perfect Black Visual Cryptography Schemes

Visual cryptography schemes such that, in the reconstructed image, all the subpixels associated with a black pixel are black, i.e., l − 0, are referred either to as visual cryptography schemes with perfect reconstruction of black pixels or to as maximal contrast schemes. For example, the (k, k)-threshold VCS described in Section 9.2.1. has perfect reconstruction of black pixels. A perfect reconstruction of both black and white pixels, which would correspond to visual cryptography schemes having ideal contrast, is impossible. Indeed, in [11] it has been shown that any (k, k)-threshold VCS has a pixel expansion of at least 2^k−1 and the relative difference (h − l)/m between reconstructed white and reconstructed black is at most 1/2^k−1. This means that, in the reconstructed white pixel, for any 2^k−1 subpixels, there is at most a white subpixel.

Visual cryptography schemes with perfect reconstruction of black pixels have been analyzed in |12, 4, 3|. In particular, in |3| it was shown how to construct (Г_Qual, Г_Forb)-VCSs with perfect reconstruction of black pixels having a pixel expansion $m = \sum_{X \in Γ_{Qual}} 2^{| X | - 1},$ $m = \sum_{X \in Γ_{Qual}} 2^{| X | - 1},$ by using a technique proposed in [1]. More precisely, such a technique to constructs visual cryptography schemes with a perfect reconstruction of black pixels using small schemes as building blocks in the construction of larger schemes, as explained in the following. For i − 1,..., q, let $(Γ_{Qual}^{i}, Γ_{Forb}^{i})$ $(Γ_{Qual}^{i}, Γ_{Forb}^{i})$ be an access structure on a set P of n participants. If a participant j ∈ P is not essential for the i-th access structure, we assume that $j \notin Γ_{Forb}^{i}$ $j \notin Γ_{Forb}^{i}$ and that j does not receive any share. Suppose there exists a ( $Γ_{Qual}^{i}, Γ_{Forb}^{i}$ $Γ_{Qual}^{i}, Γ_{Forb}^{i}$ )-VCS with a pixel expansion m_i and basis matrices $T_{i}^{0}$ $T_{i}^{0}$ and $T_{i}^{1}$ $T_{i}^{1}$ , for each i − 1,..., q. The basis matrix S⁰ (S¹, resp.) of a VCS for the access structure (Г_Qual, Г_Forb) where $Γ_{Qual} = Γ_{Qual}^{1} \cup \dots \cup Γ_{Qual}^{q}$ $Γ_{Qual} = Γ_{Qual}^{1} \cup \dots \cup Γ_{Qual}^{q}$ and $Γ_{Forb} = Γ_{Forb}^{1} \cap \dots \cap Γ_{Forb}^{q}$ $Γ_{Forb} = Γ_{Forb}^{1} \cap \dots \cap Γ_{Forb}^{q}$ is constructed as the concatenation of some auxiliary matrices ${\hat{T}}_{i}^{0} ({\hat{T}}_{i}^{1}, resp .)$ ${\hat{T}}_{i}^{0} ({\hat{T}}_{i}^{1}, resp .)$ , for each i − 1,..., q. Such matrices are obtained as follows: for each j − 1,..., n, the j-th row of ${\hat{T}}_{i}^{0}$ ${\hat{T}}_{i}^{0}$ ( ${\hat{T}}_{i}^{1}$ ${\hat{T}}_{i}^{1}$ , resp.) has all ones as entries if the participant j is not essential for ( $Γ_{Qual}^{i}, Γ_{Forb}^{i}$ $Γ_{Qual}^{i}, Γ_{Forb}^{i}$ ), otherwise it is the row of $T_{i}^{0}$ $T_{i}^{0}$ ( $T_{i}^{1}$ $T_{i}^{1}$ , resp.) corresponding to participant j. Hence, $s^{0} = {\hat{T}}_{1}^{0} \circ {\hat{T}}_{2}^{0} \circ \dots \circ {\hat{T}}_{q}^{0}$ $s^{0} = {\hat{T}}_{1}^{0} \circ {\hat{T}}_{2}^{0} \circ \dots \circ {\hat{T}}_{q}^{0}$ and $s^{1} = {\hat{T}}_{1}^{1} \circ {\hat{T}}_{2}^{1} \circ \dots \circ {\hat{T}}_{q}^{1}$ $s^{1} = {\hat{T}}_{1}^{1} \circ {\hat{T}}_{2}^{1} \circ \dots \circ {\hat{T}}_{q}^{1}$ , where o denotes the concatenation of matrices. The resulting VCS has a pixel expansion $m = \sum_{i = 1}^{q} m_{i}$ $m = \sum_{i = 1}^{q} m_{i}$ . For a special class of access structures, such as threshold access structures and graph-based access structures, it is possible to design VCSs with the perfect reconstruction of black pixels achieving a smaller value of m, as shown in [1,12,3].

Example 2 Let P = {1, 2, 3, 4} and Г₀ = {{1, 2}, {2, 3}, {3,4}}. We can construct a VCS with a perfect reconstruction of black pixels for the access structure having basis Г₀ by using three (2, 2)-threshold VCSs on the sets of participants {1, 2}, {2, 3}, and {3, 4}. The basis matrices T⁰ and T¹ for the (2, 2)-threshold VCS described in Section 9.2.1. are

\begin{matrix} T^{0} = [\begin{matrix} 1 & 0 \\ 1 & 0 \end{matrix}] & T^{1} = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] . \end{matrix}

$\begin{matrix} T^{0} = [\begin{matrix} 1 & 0 \\ 1 & 0 \end{matrix}] & T^{1} = [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] . \end{matrix}$

From T⁰ and T¹ we construct the pair of matrices ( ${\hat{T}}_{i}^{0}$ ${\hat{T}}_{i}^{0}$ , ${\hat{T}}_{i}^{1}$ ${\hat{T}}_{i}^{1}$ ), for i = 1,..., 3 having four rows each, as follows:

\begin{matrix} {\hat{T}}_{1}^{0} = [\begin{array}{l} 1 & 0 \\ 1 & 0 \\ 1 & 1 \\ 1 & 1 \end{array}] & {\hat{T}}_{1}^{1} = [\begin{array}{l} 1 & 0 \\ 0 & 1 \\ 1 & 1 \\ 1 & 1 \end{array}], \end{matrix}

$\begin{matrix} {\hat{T}}_{1}^{0} = [\begin{array}{l} 1 & 0 \\ 1 & 0 \\ 1 & 1 \\ 1 & 1 \end{array}] & {\hat{T}}_{1}^{1} = [\begin{array}{l} 1 & 0 \\ 0 & 1 \\ 1 & 1 \\ 1 & 1 \end{array}], \end{matrix}$

\begin{matrix} \begin{matrix} {\hat{T}}_{2}^{0} = [\begin{array}{l} 1 & 1 \\ 1 & 0 \\ 1 & 0 \\ 1 & 1 \end{array}] & {\hat{T}}_{2}^{1} = [\begin{array}{l} 1 & 1 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{array}], \end{matrix} \\ \begin{matrix} {\hat{T}}_{3}^{0} = [\begin{array}{l} 1 & 1 \\ 1 & 1 \\ 1 & 0 \\ 1 & 0 \end{array}] & {\hat{T}}_{3}^{1} = [\begin{array}{l} 1 & 1 \\ 1 & 1 \\ 1 & 0 \\ 0 & 1 \end{array}] . \end{matrix} \end{matrix}

$\begin{matrix} \begin{matrix} {\hat{T}}_{2}^{0} = [\begin{array}{l} 1 & 1 \\ 1 & 0 \\ 1 & 0 \\ 1 & 1 \end{array}] & {\hat{T}}_{2}^{1} = [\begin{array}{l} 1 & 1 \\ 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{array}], \end{matrix} \\ \begin{matrix} {\hat{T}}_{3}^{0} = [\begin{array}{l} 1 & 1 \\ 1 & 1 \\ 1 & 0 \\ 1 & 0 \end{array}] & {\hat{T}}_{3}^{1} = [\begin{array}{l} 1 & 1 \\ 1 & 1 \\ 1 & 0 \\ 0 & 1 \end{array}] . \end{matrix} \end{matrix}$

Concatenating the matrices ${\hat{T}}_{1}^{0}$ ${\hat{T}}_{1}^{0}$ , ${\hat{T}}_{2}^{0}$ ${\hat{T}}_{2}^{0}$ , and ${\hat{T}}_{3}^{0}$ ${\hat{T}}_{3}^{0}$ we obtain the basis matrix S⁰

s^{0} = [\begin{array}{l} 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 & 0 \end{array}],

$s^{0} = [\begin{array}{l} 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 & 0 \end{array}],$

whereas, concatenating the matrices ${\hat{T}}_{1}^{1}$ ${\hat{T}}_{1}^{1}$ , ${\hat{T}}_{2}^{1}$ ${\hat{T}}_{2}^{1}$ , and ${\hat{T}}_{3}^{1}$ ${\hat{T}}_{3}^{1}$ we obtain the basis matrix S¹

s^{1} = [\begin{array}{l} 1 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 & 1 \end{array}] .

$s^{1} = [\begin{array}{l} 1 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 & 1 \end{array}] .$

The pixel expansion of the above construction is $m = \sum_{X \in Γ_{0}} 2^{| X | - 1} = 6$ $m = \sum_{X \in Γ_{0}} 2^{| X | - 1} = 6$ .

9.3 Almost Ideal Contrast VCS with Reversing

In order to improve the contrast in VCSs, Viet and Kurosawa [13] introduced another noncryptographic operation, called reversing, which can be used by participants in the reconstruction phase. Such an operation, which can be easily performed by many copy machines, is applied to a transparency and creates another transparency in which black pixels are reversed to white pixels and viceversa. In the following, we will denote by l, the transparency obtained after applying the reversing operation to the transparency t.

Viet and Kurosawa [13] showed how to construct a (Г_Qual, Г_Forb)-VCS with reversing, where black pixels are perfectly reconstructed, whereas, white pixels are almost perfectly reconstructed. The idea behind their construction is to run several times the distribution phase of a (Г_Qual, Г_Forb)-VCS with a perfect reconstruction of black pixels. The larger the number c of runs, the better the contrast of the resulting VCS with reversing. In particular, Viet and Kurosawa showed that if the contrast of the underlying VCS is q < 1, then the contrast in their VCS with reversing is on the average q^c. The price to pay to get an almost ideal contrast is the number of transparencies stored by each participant, which corresponds to the number c of runs. Moreover, there is a loss of resolution in their scheme, since each pixel in the original image corresponds to m subpixels in the reconstructed image, where m denotes the pixel expansion of the underlying VCS.

In the distribution phase of the VCS with reversing in |13|, the encoding of the secret image is handled pixel by pixel, where each pixel is considered independently of the others. For each pixel of the original image, the dealer runs c times independently a (Г_Qual, Г_Forb)-VCS with a perfect reconstruction of black pixels and pixel expansion m; we denote by $s_{i}^{ℓ}$ $s_{i}^{ℓ}$ the share for participant i in run l, for i − 1 , . . . , n and l − 1 , . . . , c (notice that the transparency corresponding to such a share contains m subpixels for each pixel of the original image). In the reconstruction phase, any qualified set of participants can recover the original secret image by performing a sequence of stacking and reversing operations on their transparencies. The construction is described in Figure 9.1.

Images

FIGURE 9.1
A construction for almost ideal contrast (Г_Qual, Г_Forb)-VCS with reversing.

Notice that in the VCS with reversing described in Figure 9.1, the computation of the reconstructed pixel $\bar{β}$ $\bar{β}$ corresponds to performing c − 1 AND operations, since $\bar{β} = \bar{O R ({\bar{α}}^{1}, \dots, {\bar{α}}^{c})} = A N D (α^{1}, \dots, α^{c})$ $\bar{β} = \bar{O R ({\bar{α}}^{1}, \dots, {\bar{α}}^{c})} = A N D (α^{1}, \dots, α^{c})$ . From the truth table of the AND operator, it follows that the reconstructed pixel $\bar{β}$ $\bar{β}$ will be black only when α¹,..., α^c are all black. Since each α^l corresponds to a reconstructed pixel in the l-th run of the underlying VCS with a perfect reconstruction of black pixels, it follows that in the case a black pixel has been shared by the dealer, the reconstructed pixel $\bar{β}$ $\bar{β}$ will be black no matter how many AND operations have been performed. On the other hand, in the case a white pixel has been shared, the reconstructed pixel $\bar{β}$ $\bar{β}$ will increasily become whiter with the execution of the runs. Thus, if the contrast of the underlying VCS with a perfect reconstruction of black pixels is q < 1, then the contrast in the VCS with reversing described in Figure 9.1 is on the average q^c.

The security of the scheme directly follows from the security of the underlying VCS.

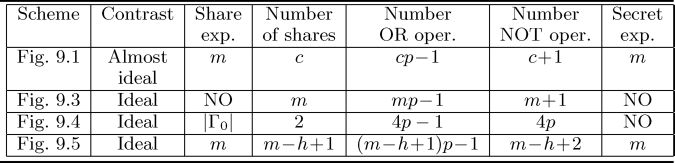
It is easy to see that the reconstruction phase requires a qualified set of p participants to perform exactly c | 1 reversing operations and cp − 1 stacking operations. Finally, notice that in the construction of Figure 9.1 there is a loss of resolution, since each pixel in the original image corresponds to m subpixels in the reconstructed image, where m denotes the pixel expansion of the underlying VCS. For example, in the (k, k)-threshold VCS with reversing resulting from the above construction, each pixel of the original image corresponds to 2^k−1 subpixels in the reconstructed image.

Example 3 Let P = {1, 2, 3,4} and Г₀ = {1, 2}, {2, 3}, {3, 4}}. The basis matrices S⁰ and S¹ in a VCS realizing the access structure Г_Qual whose basis is Г₀ are:

\begin{matrix} s^{0} = [\begin{array}{l} 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{array}] & s^{1} = [\begin{array}{l} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array}] . \end{matrix}

$\begin{matrix} s^{0} = [\begin{array}{l} 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{array}] & s^{1} = [\begin{array}{l} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array}] . \end{matrix}$

The collections C₀ and C₁ are obtained by permuting the columns of the corresponding basis matrix (S⁰ for C₀, and S¹ for C₁) in all possible ways. First, consider two rounds where the shares generated for participant 1 are $s_{1}^{1} = 0110$ $s_{1}^{1} = 0110$ , $s_{1}^{2} = 1100$ $s_{1}^{2} = 1100$ whereas, the shares generated for the participant 2 are $s_{2}^{1} = 0111$ $s_{2}^{1} = 0111$ , $s_{2}^{2} = 1101$ $s_{2}^{2} = 1101$ . During the reconstruction phase, the two participants stack their shares and retrieve $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 0111$ $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 0111$ , $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1101$ $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1101$ . By applying the reversing operation to each a^j and stacking the results, they obtain $β = O R (\bar{0111}, \bar{1101}) = 1010$ $β = O R (\bar{0111}, \bar{1101}) = 1010$ . By reversing β, they obtain $\bar{β} = 0101$ $\bar{β} = 0101$ , and reconstruct a white pixel that consists of two out of four white subpixels. Now, let’s add a third round. Assume that the extra shares for participants 1 and 2 are $2 a r e s_{1}^{3} = 1001$ $2 a r e s_{1}^{3} = 1001$ and $s_{2}^{3} = 1011$ $s_{2}^{3} = 1011$ , respectively. During the reconstruction phase, the two participants stack their shares and retrieve $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 0111$ $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 0111$ , $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1101, α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 1011$ $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1101, α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 1011$ . By applying the reversing operation to each α^j and stacking the results, they obtain $β = O R (\bar{0111}, \bar{1101}, \bar{1011}) = 1110$ $β = O R (\bar{0111}, \bar{1101}, \bar{1011}) = 1110$ . By reversing β, they obtain $\bar{β} = 0001$ $\bar{β} = 0001$ , and reconstruct a white pixel that consists of three out of four white subpixels. Then, with an extra round the whiteness of the reconstructed pixel increases.

Let S¹ be the matrix chosen by the dealer to share a black pixel. Consider two rounds. The shares generated for participant 1 are $s_{1}^{1} = 1001$ $s_{1}^{1} = 1001$ , $s_{1}^{2} = 1100$ $s_{1}^{2} = 1100$ , whereas, the shares generated for the participant 2 are $s_{2}^{1} = 1110$ $s_{2}^{1} = 1110$ , $s_{2}^{2} = 0111$ $s_{2}^{2} = 0111$ . During the reconstruction phase, the two participants stack their shares and retrieve $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 1111$ $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 1111$ , $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1111$ $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1111$ . By applying the reversing operation to each a? and stacking the results, they obtain $β = O R (\bar{1111}, \bar{1111}) = 0000$ $β = O R (\bar{1111}, \bar{1111}) = 0000$ . By reversing β, they obtain $\bar{β} = 1111$ $\bar{β} = 1111$ , and perfectly reconstruct a black pixel. It is easy to see that, by increasing the amount of rounds, the reconstruction of a black pixel continues to be perfect.

9.4 Ideal Contrast VCS with Reversing

The scheme proposed by Viet and Kurosawa [13] is said to have an almost ideal contrast because the black pixels are perfectly reconstructed, whereas, the white ones are almost perfectly reconstructed. The larger the number of runs, the more the whiteness of the reconstructed white pixels. However, a perfect reconstruction of both black and white pixels, corresponding to an ideal contrast, cannot be achieved by their scheme, even for a large number of runs. Moreover, the scheme proposed by Viet and Kurosawa [13] also has the following drawbacks:

Each participant is required to store c transparencies, where c denotes the number of runs for the underlying VCS;
The size of each transparency is m times the size of the original image, where m denotes the pixel expansion of the underlying VCS;
There is a loss of resolution in the reconstructed image;
A large number of runs is required to obtain an almost ideal contrast;
The underlying VCS has to be perfect black.

In this section we describe different solutions for VCSs with reversing all achieving ideal contrast. Each solution further improves on the proposal by Viet and Kurosawa [13] by overcoming some of the above drawbacks. The first solution, described in Section 9.4.1., uses the fact that the introduction of the reversing operation allows participants to compute any Boolean function of their transparencies and uses as a building block a binary secret sharing scheme. The schemes described in Section 9.4.2. all use as a building block a perfect black VCS, whereas, the scheme in Section 9.4.3. is based on a non-perfect black VCS.

9.4.1 A Construction Using a Binary Secret Sharing Scheme

In this section we describe an ideal contrast VCS with reversing for any access structure (Г_Qual, Г_Forb), proposed in [6]. The scheme uses as a building block a binary secret sharing scheme (BSS for short).

A BSS for an access structure (Г_Qual, Г_Forb) on a set of n participants is a method to share a secret s ∈ {0, 1} among the n participants in such a way that only subsets of participants in Г_Qual can recover the secret, whereas, subsets of participants in Г_Forb have no information about the secret. A BSS consists of two collections B₀ and B₁ of distribution functions. A distribution function $f \in ℬ_{0} \cup ℬ_{1}$ $f \in ℬ_{0} \cup ℬ_{1}$ is a function associating each participant i to the share f(i). In the reconstruction phase, any qualified set of participants X − {i₁,...,i_p} ∈ Г_Qual run a reconstruction algorithm Rec(f(i₁),...,f(i_p))which on inputs the shares they hold, outputs the secret s. See [7] for a formal definition of BSSs. Let r be the number of bits in the binary representation of the largest share f(i). Without loss of generality (W.l.o.g.), we consider the r-bits binary representation of each share f(j), where j ≠ i, obtained by prefixing the r′-bits binary representation of f(j), where r′ < r, with r − r' zeroes. The reconstruction algorithm Rec(f(i₁),...,f(i_p))computes a Boolean function on its inputs. Such a function can be computed by using a Boolean circuit. It is well known that OR and NOT represent a complete basis for Boolean functions, i.e., any Boolean function can be computed by a binary circuit composed only of OR and NOT gates. Therefore, Rec(f(i₁),...,f(i_p))can be computed by a Boolean circuit composed only of OR and NOT gates, corresponding to stacking and reversing operations, respectively.

In the distribution phase of the VCS with reversing, the encoding of the secret image is handled pixel by pixel, where each pixel is considered independently of the others. For each pixel of the original image and for each participant i, the dealer generates the corresponding pixel in each transparency t_i,1, . . ., t_i,r, where r is the size of the shares distributed by the underlying BSS. In the reconstruction phase, any qualified set of participants recover the original secret image with no loss of resolution by performing a sequence of stacking and reversing operations on their transparencies. Such a sequence of operations corresponds to simulating parallel runs of the reconstruction algorithm of the BSS, that is, one run for each pixel of the original image. Such a parallel execution enables the reconstruction of the original image, because each transparency contains the same number of pixels of the original image and each pixel can be reconstructed by using the same Boolean circuit. The construction is described in Figure 9.2.

It is easy to see that the construction of Figure 9.2 gives an ideal contrast VCS with reversing with no loss of resolution. Indeed, let us consider the encoding pixel by pixel. Let X ∈ Г_Qual be a qualified set of participants. From the reconstruction property of the underlying BSS, the participants in X can reconstruct the secret pixel, by performing the sequence of stacking and reversing operations on their transparencies corresponding to the binary circuit simulating the reconstruction algorithm of the underlying BSS. The security of the scheme directly follows from the security of the underlying BSS.

Images

FIGURE 9.2
A construction for ideal contrast VCS with reversing using a BSS.

As shown in the following, we can construct an ideal contrast (k, k)-threshold VCS with reversing, with k ≥ 2, where each participant has to store only one transparency, if we use as a building block a (k, k)-threshold BSS distributing shares of one bit. This improves on the construction for a (k, k)-threshold VCS with reversing of Figure 9.1, where each participant has to store c transparencies, each containing 2^k−1 subpixels for each pixel of the original secret image, c being the number of runs of the underlying VCS needed to obtain an asymptotically ideal contrast. Indeed, consider the following (k, k)-threshold BSS: to share a secret s ∈ {0, 1}, the dealer randomly chooses k − 1 random bits s₁,..., s_k−1 and computes s_k − s ⊝ s₁ ⊕ - - - ⊕ s_k−1, where ⊕ denotes the XOR operation. For i = 1,..., k, the share for participant i is the bit s_i. In order to reconstruct the secret s in the BSS the k participants are required to compute the XOR of their shares s₁ ⊕ - - - ⊝ s_k. By arranging the k > 2 bits s₁,..., s_k as the leaves of a binary tree of height [log k], where internal nodes have two children and the leaves are distributed on at most two levels, the problem of computing the XOR of k bits can be reduced to the problem of computing k − 1 pairwise XORs, corresponding to the internal nodes of the tree. Since each pairwise XOR operation can be expressed in terms of 3 ORs and 4 NOTs as follows:

s_{i} \oplus s_{j} = O R (\bar{O R (\bar{s_{i}}, s_{j})}, \bar{O R (s_{i}, \bar{s_{j}})}),

$s_{i} \oplus s_{j} = O R (\bar{O R (\bar{s_{i}}, s_{j})}, \bar{O R (s_{i}, \bar{s_{j}})}),$

then, the computation of each pairwise XOR can be performed by using a Boolean circuit, having a depth 4, constituted only by OR and NOT gates. Therefore, the computation of s₁ ⊕ - - - ⊕ s_k can be performed by a Boolean circuit having a depth 4 [log k].

In the corresponding VCS with reversing, for each pixel of the original image, the dealer runs the distribution phase of the BSS, and, for each participant i, generates on the transparency t_i the pixel corresponding to the share s_i distributed by the BSS. In order to reconstruct the secret image, the k participants are involved in a computation consisting of stacking and reversing their transparencies, simulating the circuit computing the XOR, which is composed only by OR and NOT gates. It is easy to see that the number of reversing and stacking operations needed to reconstruct the secret image is equal to 4(k−1) and 3(k−1), respectively.

Example 4 Let k = 4. If the dealer wants to share a white pixel, he runs the distribution phase of the BSS for the secret s = 0. Hence, he randomly chooses three bits s₁, s₂, and s₃, and computes s₄ = s ⊝ s₁ ⊝ s₂ ⊕ s₃. For example, let s₁ = 1, s₂ = 0, s₃ = 0, then s₄ = 1. The corresponding pixels in the transparencies t₁, t₂, t₃, t₄ are equal to 1, 0, 0, 1, respectively. In order to reconstruct the secret pixel, the participants have to simulate the computation of s₁ ⊕ s₂ ⊕ s₃ ⊕ s₄ by performing a sequence of stacking and reversing operations on their transparencies. Notice that s = s₁ ⊕ s₂ ⊕ s₃ ⊕ s₄ = (s₁ ⊕ s₂) ⊕ (s₃ ⊕ s₄). Since $a = s_{1} \oplus s_{2} = O R (\bar{O R (\bar{s_{1}}, s_{2})}, \bar{O R (s_{1}, \bar{s_{2}})}) = 1$ $a = s_{1} \oplus s_{2} = O R (\bar{O R (\bar{s_{1}}, s_{2})}, \bar{O R (s_{1}, \bar{s_{2}})}) = 1$ and $b = s_{3} \oplus s_{4} = O R (\bar{O R (\bar{s_{3}}, s_{4})}, \bar{O R (s_{3}, \bar{s_{4}})}) = 1$ $b = s_{3} \oplus s_{4} = O R (\bar{O R (\bar{s_{3}}, s_{4})}, \bar{O R (s_{3}, \bar{s_{4}})}) = 1$ , it follows that the four participants can reconstruct the secret pixel corresponding to the secret $s = a \oplus b = O R (\bar{O R (\bar{a}, b)}, \bar{O R (a, \bar{b})}) = 0$ $s = a \oplus b = O R (\bar{O R (\bar{a}, b)}, \bar{O R (a, \bar{b})}) = 0$ by performing 12 reversing operations and 9 stacking operations.

9.4.2 Constructions Using Perfect Black VCSs

In this section we describe different constructions using as a building block a perfect black VCS. In particular, the solution described in Section 9.4.2.1 requires each participant to store m transparencies, where m denotes the pixel expansion of the underlying perfect black VCS, and offers no loss of resolution. The scheme described in Section 9.4.2.2 still offers no loss of resolution, but requires each participant to hold two transparencies having a large size, i.e., |Г₀| times the size of the secret image. Finally, the scheme in Section 9.4.2.3 reduces the number of transparencies stored by each participant to m − h + 1, but there is a loss of resolution on the reconstructed image.

9.4.2.1 The Scheme by Cimato, De Santis, Ferrara, and Masucci

In this section we describe a general technique, due to Cimato, De Santis, Ferrara, and Masucci [6], to construct an ideal contrast VCS with reversing for any access structure (Г_Qual, Г_Forb) The scheme uses as a building block a VCS with perfect reconstruction of black pixels, having a certain pixel expansion m, and requires each participant to store m transparencies, each having the same number of pixels as the original image.

In the distribution phase of the scheme, the encoding of the secret image is handled pixel by pixel, where each pixel is considered independently of the others. For each pixel of the original image and for each participant i, the dealer generates the corresponding pixel in each transparency t_i,1,..., t_i,m. In the reconstruction phase, any qualified set of participants recover the original secret image with no loss of resolution by performing a sequence of stacking and reversing operations on their transparencies. The construction is described in Figure 9.3.

Images

FIGURE 9.3
Cimato, De Santis, Ferrara, and Masucci’s ideal contrast VCS with reversing.

It is easy to see that the construction of Figure 9.3 gives an ideal contrast (Г_Qual, Г_Forb)-VCS with reversing. Indeed, let us consider the encoding pixel by pixel and analyze separately the reconstruction phase in case the dealer shared a white pixel or a black pixel. Let X − {i₁,..., i_p} ∈ Г_Qual be a qualified subset of participants and assume that the secret pixel shared by the dealer was white. From Property 1. of Definition 1, there exists an index j ∈ {1, ..., m} for which the encoded pixels in each transparency $t_{i_{1}}, j, \dots, t_{i_{p}}, j$ $t_{i_{1}}, j, \dots, t_{i_{p}}, j$ are all white. It follows that for the same j, αi − 0 and $β = O R (\bar{α_{1}}, \dots, \bar{α_{m}})$ $β = O R (\bar{α_{1}}, \dots, \bar{α_{m}})$ is equal to 1. Then, $\bar{β}$ $\bar{β}$ is zero, i.e., the reconstructed pixel will be white. Now, assume that the secret pixel shared by the dealer was black. Since the underlying scheme is a (Г_Qual, Г_Frob)-VCS with a perfect reconstruction of black pixels, it holds that α_j = 1, for j = 1, ..., m. Hence, $β = O R (\bar{α_{1}}, \dots, \bar{α_{m}})$ $β = O R (\bar{α_{1}}, \dots, \bar{α_{m}})$ is zero and $\bar{β} = 1$ $\bar{β} = 1$ , i.e., the reconstructed pixel will be black. The security of the scheme directly follows from the security of the underlying VCS.

Compared to the scheme described in Figure 9.1, the one of Figure 9.3 requires each participant to store m transparencies, each having the same number of pixels as the original image. Furthermore, the scheme requires a qualified set of p participants to execute exactly m + 1 reversing operations and mp — 1 stacking operations. Finally, the reconstructed image has no loss of resolution.

Example 5 Let P − {1, 2, 3,4} and Г₀ − {{1, 2}, {2, 3}, {3, 4}}. The basis matrices S⁰ and S¹ in a VCS realizing the access structure Г_Qual whose basis is Г₀ are:

\begin{matrix} s^{0} = [\begin{array}{l} 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{array}] & s^{1} = [\begin{array}{l} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array}] . \end{matrix}

The collections C₀ and C₁ are obtained by permuting the columns of the corresponding basis matrix (S⁰ for C₀, and S¹ for C₁) in all possible ways. Let S⁰ be the matrix chosen by the dealer to share a white pixel. The corresponding pixels generated for the transparencies t_1,1, ..., t_1,4 for participant 1 are 0, 1, 1, and 0, whereas, the pixels generated for the transparencies t_2,1, ..., t_2,4 for participant 2 are 0, 1, 1, and 1. During the reconstruction phase, the two participants stack their shares and retrieve α₁ = 0, α₂ = 1, α₃ = 1, α₄ = 1. By applying the reversing operation to each α_j and stacking the results, they obtain $β = O R (\bar{0}, \bar{1}, \bar{1}, \bar{1}) = 1$ $β = O R (\bar{0}, \bar{1}, \bar{1}, \bar{1}) = 1$ . By reversing β, they obtain $\bar{β} = 0$ $\bar{β} = 0$ , and reconstruct a white pixel.

Let S¹ be the matrix chosen by the dealer to share a black pixel. The corresponding pixels generated for the transparencies t_1,1, ..., t_1,4 for participant 1 are 1 , 0, 0, and 1 , whereas, the corresponding pixels generated for the transparencies t_2,1, ... , t_2,4 for participant 2 are 111, and 0. During the reconstruction phase, the two participants will perform the same operation sequence as before, retrieving α₁ = 1, α₂ = 1, α₃ = 1, α₄ = 1, $β = O R (\bar{1}, \bar{1}, \bar{1}, \bar{1}) = 0$ $β = O R (\bar{1}, \bar{1}, \bar{1}, \bar{1}) = 0$ , and $\bar{β} = 1$ $\bar{β} = 1$ , reconstructing a black pixel.

Notice that if the qualified set X ∈ Г_Qual is a superset of an X′ ∈ Г₀, then, in the reconstruction phase, participants in X can recover the secret image by performing the given sequence of operations on the subset of transparencies held by participants in X′ only, thus reducing the total number of operations. A further improvement can be obtained by considering as a building block a (Г_Qual, Г_Forb)-VCS with a perfect reconstruction of black pixels having a smaller pixel expansion than $m = \sum_{X \in Γ_{Qual}} 2^{| X | - 1}$ $m = \sum_{X \in Γ_{Qual}} 2^{| X | - 1}$ . In particular, by considering the set Г₀ of all the minimal qualified subsets, and by using the same technique proposed in [1], it is possible to construct a (Г_Qual, Г_Forb)-VCS with a perfect reconstruction of black pixels, having pixel expansion $m^{'} = \sum_{X \in Γ_{0}} 2^{| X | - 1}$ $m^{'} = \sum_{X \in Γ_{0}} 2^{| X | - 1}$ , thus reducing the number of transparencies held by each participant.

9.4.2.2 The Scheme by Hu and Tzeng

In this section we describe an ideal contrast VCS with reversing for any access structure (Г_Qual, Г_Forb), due to Hu and Tzeng [9]. The construction uses the basis matrices of the Naor-Shamir’s (k, k)-VCS described in Section 9.2.1. along with the properties of the XOR operator.

Let S⁰ and S¹ be the basis matrices of the Naor-Shamir’s (k, k)-VCS. The key idea behind Hu and Tzeng’s construction relies upon the fact that the XOR of the bits belonging to a column of S⁰ (S¹, respectively) is zero (one, respectively). With such an observation in mind, a (k, k)-VCS with reversing may be easily constructed by issuing to the participant i a transparency of the same size as the original image constructed as follows: for each white (black, respectively) pixel the dealer chooses a column in S⁰ (S¹, respectively) and puts on the transparency the i-th item of the chosen column. Since each column of S⁰ (S¹ , respectively) has an even (odd, respectively) number of ones, it is easy to see that by XORring k transparencies the original image is reconstructed without any loss of resolution. In the following we refer to this construction as the XOR-(k, k)-VCS. As seen in Section 9.4.1., the problem of computing the XOR of k transparencies can be reduced to a sequence of stacking and reversing operations.

By using |Г₀| executions of the XOR-(k, k)-VCS, a naive VCS with reversing for any access structure (Г_Qual, Г_Forb) can be obtained. Indeed, we simply execute the above XOR-(|X|, |X|)-VCS for each qualified set X ∈ Г₀. Such a solution requires each participant to store as many transparencies as the number of qualified sets he belongs to. Each transparency has the same size as the original image, on the other hand, each participant needs to keep track of the correspondence between a transparency and the related qualified set. In order to overcome such a drawback, Hu and Tzeng proposed a way to combine the transparencies distributed to a participant in a single transparency. Such a transparency is then used by a participant in a qualified set along with an additional transparency to reconstruct the original image. Both transparencies held by each participant are |Г₀| times larger than the size of the secret image. Indeed, each transparency contains |Г₀| blocks and each qualified subset of participants reconstructs, without loss of resolution, the secret image in a single block, whereas the other reconstructed blocks contain only white pixels. Compared to the naive solution, the scheme introduces some computational overhead by requiring additional stacking and reversing operations.

In the distribution phase, for each qualified set X in Г₀ and each participant i ∈ X the dealer generates the subtransparency t_X,i resulting by applying the XOR-(|X|, |X|)-VCS on the set of participants X. For each set X in Г₀ such that the participant i does not belong to X, the dealer generates the subtransparency t_X,i consisting of all ones. Each participant i receives a transparency t_i corresponding to the concatenation of its sub-transparency according to an ordering over the qualified sets in Г₀. Hence, let X₁,..., X_|Г0| be the qualified sets in Г₀, each participant i receives the transparency $t_{i} = t_{X_{1}}, i \circ \dots \circ t_{X_{| Γ_{0} |}}, i$ $t_{i} = t_{X_{1}}, i \circ \dots \circ t_{X_{| Γ_{0} |}}, i$ , where o denotes the concatenation between transparencies. Each participant i also receives an additional transparency ${t^{'}}_{i}$ ${t^{'}}_{i}$ of the same size as t_i such that each subtransparency ${t^{'}}_{X, i}$ ${t^{'}}_{X, i}$ has all ones if the participant i does not belong to the qualified set X whereas it (to repeat the subject that is each sub transparency) has all zeros, otherwise. The construction is described in Figure 9.4.

Images

FIGURE 9.4
Hu and Tzeng’s ideal contrast VCS with reversing.

It is easy to see that the i-th qualified set obtains the original image in place of the i-th subtransparency of U′ while all other subtransparencies contains all zeros. Indeed, the matrix corresponding to the i-th subtransparency of U′ is the same as the i-th subtransparency of T, which from the property of the XOR operator and the composition of the Naor-Shamir basis matrices corresponds to the original image. Moreover, the matrices corresponding to the subtransparency of U but the i-th one contains all ones. Hence, from the property of the XOR operator such subtransparencies contains all zeros in U′.

The reconstruction phase requires a qualified set of p participants to perform exactly 4p reversing operations and 4p − 1 stacking operations, since, as seen in Section 9.4.1., the XOR operation can be implemented by means of 3 ORs and 4 NOTs operations.

Example 6 Let P = {1, 2, 3, 4}, Г₀ = {X₁, X₂} = {{1, 4}, {2, 3, 4}}}. Let $s_{1}^{0}$ $s_{1}^{0}$ and $s_{1}^{1}$ $s_{1}^{1}$ be the basis matrices associated to the XOR-(2,2)-VCS for X₁ and let $s_{2}^{0}$ $s_{2}^{0}$ and $s_{2}^{1}$ $s_{2}^{1}$ be the basis matrices associated with the XOR-(3,3)-VCS for X₂ defined as follows:

\begin{matrix} \begin{matrix} s_{1}^{0} = [\begin{array}{l} 1 & 0 \\ 1 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}] & s_{1}^{1} = [\begin{array}{l} 1 & 0 \\ 1 & 1 \\ 1 & 1 \\ 0 & 1 \end{array}]; \end{matrix} \\ \begin{matrix} s_{1}^{0} = [\begin{array}{l} 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{array}] & s_{2}^{1} = [\begin{array}{l} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array}] . \end{matrix} \end{matrix}

$\begin{matrix} \begin{matrix} s_{1}^{0} = [\begin{array}{l} 1 & 0 \\ 1 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}] & s_{1}^{1} = [\begin{array}{l} 1 & 0 \\ 1 & 1 \\ 1 & 1 \\ 0 & 1 \end{array}]; \end{matrix} \\ \begin{matrix} s_{1}^{0} = [\begin{array}{l} 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{array}] & s_{2}^{1} = [\begin{array}{l} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array}] . \end{matrix} \end{matrix}$

Let $I = [\begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 0 \end{matrix}]$ $I = [\begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 0 \end{matrix}]$ be the original image. The transparencies are computed as follows:

\begin{array}{l} t_{1} = [\begin{array}{l} 1 & 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \end{array}] & {t^{'}}_{1} = [\begin{array}{l} 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{array}] \\ t_{2} = [\begin{array}{l} 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 & 1 \end{array}] & {t^{'}}_{2} = [\begin{array}{l} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \end{array}] \\ t_{3} = [\begin{array}{l} 1 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 0 \end{array}] & {t^{'}}_{3} = [\begin{array}{l} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \end{array}] \\ t_{4} = [\begin{array}{l} 0 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \end{array}] & {t^{'}}_{4} = [\begin{array}{l} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}] \end{array}

$\begin{array}{l} t_{1} = [\begin{array}{l} 1 & 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \end{array}] & {t^{'}}_{1} = [\begin{array}{l} 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{array}] \\ t_{2} = [\begin{array}{l} 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 & 0 & 1 \end{array}] & {t^{'}}_{2} = [\begin{array}{l} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \end{array}] \\ t_{3} = [\begin{array}{l} 1 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 & 0 \end{array}] & {t^{'}}_{3} = [\begin{array}{l} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \end{array}] \\ t_{4} = [\begin{array}{l} 0 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \end{array}] & {t^{'}}_{4} = [\begin{array}{l} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}] \end{array}$

Participants in X2 = {2, 3, 4} reconstruct the original image by computing

\begin{array}{l} T = [\begin{array}{l} 1 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 0 \end{array}] & T^{'} = [\begin{array}{l} 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{array}] \\ U = [\begin{array}{l} 1 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 \end{array}] & U^{'} = [\begin{array}{l} 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \end{array}] . \end{array}

$\begin{array}{l} T = [\begin{array}{l} 1 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 0 \end{array}] & T^{'} = [\begin{array}{l} 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{array}] \\ U = [\begin{array}{l} 1 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 & 1 \end{array}] & U^{'} = [\begin{array}{l} 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \end{array}] . \end{array}$

9.4.2.3 The Scheme by Yang, Wang, and Chen

Yang, Wang, and Chen [14] proposed a different method to construct a VCS with reversing starting from any perfect black VCS with pixel expansion m. In their scheme each participant receives m − h +1 shares, where the first one corresponds to the one obtained by the underlying perfect black VCS, whereas the i-th share is obtained by cyclically shifting the (i − 1)-th share one bit to the right, for each i = 2, . . . , m − h + 1. Notice that the right shift operation can be implemented by means of OR and NOT operations, since OR and NOT represent a complete basis for Boolean functions.

The scheme is shown in Figure 9.5.

Images

FIGURE 9.5
Yang, Wang, and Chen’s ideal contrast VCS with reversing.

The reconstruction phase is the same as that of the scheme shown in Figure 9.1. Recall that the computation of the reconstructed pixel $\bar{β}$ $\bar{β}$ corresponds to performing m − h + 1 AND operations, since $\bar{β} = \bar{O R ({\bar{α}}^{1}, \dots, {\bar{α}}^{m - h + 1})} = A N D (α^{1}, \dots, α^{m - h + 1})$ $\bar{β} = \bar{O R ({\bar{α}}^{1}, \dots, {\bar{α}}^{m - h + 1})} = A N D (α^{1}, \dots, α^{m - h + 1})$ . It is easy to see that the construction of Figure 9.5 achieves a perfect reconstruction of both white and black pixels. Indeed, in the case a white pixel has been shared, α¹ contains h white subpixels and m − h black ones. The maximum interval between two 0s in α¹ is m − h, thus, by shifting right one bit (m − h) times, there is at least an αⁱ having a subpixel equal to 0 at position j, for each i = 1 , . . . , m − h + 1 and j = 1 , . . . , m. Therefore, the reconstructed pixel $\bar{β} = A N D (α^{1}, \dots, α^{m - h + 1})$ $\bar{β} = A N D (α^{1}, \dots, α^{m - h + 1})$ results in all white subpixels. On the other hand, in case a black pixel has been shared, αⁱ contains all black subpixels, for each i = 1, ..., m − h +1, thus also $\bar{β}$ $\bar{β}$ perfectly reconstructs the pixel.

The security of the scheme directly follows from the security of the underlying VCS.

The reconstruction phase requires a qualified set of p participants to perform exactly m − h +2 reversing operations and (m − h + 1)p − 1 stacking operations. Finally, notice that in the construction of Figure 9.5 there is a loss of resolution, since each pixel in the original image corresponds to m subpixels in the reconstructed image, where m denotes the pixel expansion of the underlying VCS.

Example 7 Let P = {1, 2, 3,4} and Г₀ = {{1, 2}, {2, 3}, {3, 4}}. The basis matrices S⁰ and S¹ in a VCS realizing the access structure Г_Qual whose basis is Г₀ are:

\begin{matrix} s^{0} = [\begin{array}{l} 0 & 1 & 1 & 0 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 \end{array}] & s^{1} = [\begin{array}{l} 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array}] \end{matrix} .

The collections C₀ and C₁ are obtained by permuting the columns of the corresponding basis matrix (S⁰ for C₀, and S¹ for C₁) in all possible ways. Let S⁰ be the matrix chosen by the dealer to share a white pixel. Notice that m = 4, h =1, and m − h+1 = 4. The shares generated for participant 1 are $s_{1}^{1} = 0110$ $s_{1}^{1} = 0110$ , $s_{1}^{2} = 0011$ $s_{1}^{2} = 0011$ , $s_{1}^{3} = 1001$ $s_{1}^{3} = 1001$ , and $s_{1}^{4} = 1100$ $s_{1}^{4} = 1100$ , whereas, the shares generated for the participant 2 are $s_{2}^{1} = 0111$ $s_{2}^{1} = 0111$ , $s_{2}^{2} = 1011$ $s_{2}^{2} = 1011$ , $s_{2}^{3} = 1101$ $s_{2}^{3} = 1101$ , and $s_{2}^{4} = 1110$ $s_{2}^{4} = 1110$ . During the reconstruction phase, the two participants stack their shares and retrieve $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 0111, α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1011, α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 1101$ $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 0111, α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1011, α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 1101$ , and $α^{4} = O R (s_{1}^{4}, s_{2}^{4}) = 1110$ $α^{4} = O R (s_{1}^{4}, s_{2}^{4}) = 1110$ . By applying the reversing operation to each α^j and stacking the results, they obtain $β = O R (\bar{0111}, \bar{1011}, \bar{1101}, \bar{1110}) = 1111$ $β = O R (\bar{0111}, \bar{1011}, \bar{1101}, \bar{1110}) = 1111$ . By reversing β, they obtain $\bar{β} = 0000$ $\bar{β} = 0000$ , and reconstruct a white pixel.

Let S¹ be the matrix chosen by the dealer to share a black pixel. The shares generated for participant 1 are $s_{2}^{2} = 0111$ $s_{2}^{2} = 0111$ , $s_{1}^{2} = 1100$ $s_{1}^{2} = 1100$ , $s_{1}^{3} = 0110$ $s_{1}^{3} = 0110$ , and $s_{1}^{4} = 0011$ $s_{1}^{4} = 0011$ , whereas, the shares generated for the participant 2 are $s_{2}^{1} = 1110$ $s_{2}^{1} = 1110$ , $s_{2}^{2} = 0111$ $s_{2}^{2} = 0111$ , $s_{2}^{3} = 1011$ $s_{2}^{3} = 1011$ , and $s_{2}^{4} = 1101$ $s_{2}^{4} = 1101$ . During the reconstruction phase, the two participants stack their shares and retrieve $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 1111$ $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 1111$ , $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1111, α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 1111$ $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 1111, α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 1111$ , and $α^{4} = O R (s_{1}^{4}, s_{2}^{4}) = 1111$ $α^{4} = O R (s_{1}^{4}, s_{2}^{4}) = 1111$ . By applying the reversing operation to each α^j and stacking the results, they obtain $β = O R (\bar{1111}, \bar{1111}, \bar{1111}, \bar{1111}) = 0000$ $β = O R (\bar{1111}, \bar{1111}, \bar{1111}, \bar{1111}) = 0000$ . By reversing β, they obtain $\bar{β} = 1111$ $\bar{β} = 1111$ , and reconstruct a black pixel.

9.4.2.4 Comparisons

The efficiency of a VCS with reversing is evaluated according to the following parameters: the contrast, the size (expansion) and the number of the transparencies held by each participant, the number of stacking and reversing operations, and the size (expansion) of the reconstructed image. In Table 9.1 we summarize and compare the parameters of the constructions described in Sections 9.3 and 9.4.2., which are all based on perfect black VCSs for a general access structure (Г_Qual, Г_Forb).

Table 9.1 Comparison between VCSs with reversing based on perfect black VCSs.

Images

9.4.3 A Construction Using a Nonperfect Black VCS

Yang, Wang and Chen [14] proposed a way to construct an ideal VCS with reversing when the difference h − l is odd, starting from any VCS (i.e., not necessarily a perfect black) with pixel expansion m. Each participant receives m shares, where the first one corresponds to that obtained by the underlying VCS, whereas, the i-th share is obtained by cyclically shifting the (i − 1)-th share one bit to right, for each i = 2, . . . , m. Notice that the right shift operation can be implemented by means of OR and NOT operations, since OR and NOT represent a complete basis for boolean functions.

The scheme is shown in Figure 9.5.

The construction of Figure 9.5 achieves perfect reconstruction of both white and black pixels. Indeed, in case a white pixel has been shared, α¹ contains h white subpixels and m − h black ones. By shifting right one bit m times, α¹,..., α^m are constructed in such a way that exactly (m − h) out of m have a black subpixel at position j, for each j = 1,..., m. Therefore, β = XOR(α¹,..., α^m) is the reconstructed white pixel if (m − h) is even, otherwise the reconstructed pixel is $\bar{β}$ $\bar{β}$ . On the other hand, since h − l is odd, i.e. h and l cannot be both odd or both even, if (m − h) is even (odd, resp.) it holds that m − l is odd (even, resp.). Hence, in the case a black pixel has been shared, α¹ contains l white subpixels and m − l black ones. By shifting right one bit m times, α¹,..., α^m are constructed in such a way that exactly (m − l) out of m have a black subpixel at position j, for each j = 1 , . . . , m. Therefore, β = XOR(α¹, ..., α^m) is the reconstructed black pixel if (m − h) is even, i.e., (m − l) is odd, otherwise the reconstructed pixel is $\bar{β}$ $\bar{β}$ .

Images

FIGURE 277.9
Ideal contrast VCS with reversing starting from any VCS.

The security of the scheme directly follows from the security of the underlying VCS.

The reconstruction phase requires a qualified set of p participants to perform exactly 4(m − 1) reversing operations and p − 1 + 3(m − 1) stacking operations, since as seen in Section 9.4.1. the XOR operation can be implemented by means of 3 ORs and 4 NOTs operations. Finally, notice that in the construction of Figure 9.5 there is a loss of resolution, since each pixel in the original image corresponds to m subpixels in the reconstructed image, where m denotes the pixel expansion of the underlying VCS.

Example 8 Consider a (2, 3)-threshold VCS, which is not a perfect black, where m − h is odd. Assume the basis matrices S⁰ and S¹ are:

\begin{matrix} s^{0} = [\begin{array}{l} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{array}] & s^{1} = [\begin{array}{l} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}] \end{matrix} .

$\begin{matrix} s^{0} = [\begin{array}{l} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{array}] & s^{1} = [\begin{array}{l} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}] \end{matrix} .$

The collections C₀ and C₁ are obtained by permuting the columns of the corresponding basis matrix (S⁰ for C₀, and S¹ for C₁) in all possible ways. Let S⁰ be the matrix chosen by the dealer to share a white pixel. The shares generated for participant 1 are $s_{1}^{1} = 100$ $s_{1}^{1} = 100$ , $s_{1}^{2} = 010$ $s_{1}^{2} = 010$ and $s_{1}^{3} = 001$ $s_{1}^{3} = 001$ , whereas, the shares generated for the participant 2 are $s_{2}^{1} = 100$ $s_{2}^{1} = 100$ , $s_{2}^{2} = 010$ $s_{2}^{2} = 010$ , and $s_{2}^{3} = 001$ $s_{2}^{3} = 001$ . During the reconstruction phase, the two participants stack their shares and retrieve $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 100$ $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 100$ , $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 010$ $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 010$ , and $α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 001$ $α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 001$ . By computing β = XOR(α¹, α², α³) = 111 and its reverse $\bar{β} = 000$ $\bar{β} = 000$ the two participants reconstruct a white pixel.

Let S¹ be the matrix chosen by the dealer to share a black pixel. The shares generated for participant 1 are $s_{1}^{1} = 100$ $s_{1}^{1} = 100$ , $s_{1}^{2} = 010$ $s_{1}^{2} = 010$ and $s_{1}^{3} = 001$ $s_{1}^{3} = 001$ , whereas, the shares generated for the participant 2 are $s_{2}^{1} = 010$ $s_{2}^{1} = 010$ , $s_{2}^{2} = 001$ $s_{2}^{2} = 001$ and $s_{2}^{3} = 100$ $s_{2}^{3} = 100$ . During the reconstruction phase, the two participants stack their shares and retrieve $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 110$ $α^{1} = O R (s_{1}^{1}, s_{2}^{1}) = 110$ , $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 011$ $α^{2} = O R (s_{1}^{2}, s_{2}^{2}) = 011$ , and $α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 101$ $α^{3} = O R (s_{1}^{3}, s_{2}^{3}) = 101$ . By computing β = XOR(α¹, α², α³) = 000 and its reverse $\bar{β} = 111$ $\bar{β} = 111$ the two participants reconstruct a black pixel.

9.5 Conclusions

Visual cryptography schemes are characterized by two parameters: the pixel expansion, i.e., the number of subpixels contained in each share and the contrast, which measures the difference between a black and a white pixel in the reconstructed image. While it is possible to construct schemes with perfect reconstruction of black pixels (or white pixels, respectively), it has been shown that a perfect reconstruction of both black and white pixels is infeasible. In order to improve the contrast in VCSs, Viet and Kurosawa [13] introduced an extra noncryptographic operation: the reversing operation. Specifically, they showed how to construct VCSs with reversing where the reconstruction of black (white, respectively) pixels is perfect, whereas, the reconstruction of white (black, respectively) pixels is almost perfect. Afterwards, Cimato et al. [6] showed how to construct VCSs with reversing where reconstruction of both black and white pixels is perfect. Such schemes are said to have an ideal contrast. In particular, Cimato et al. [6] proposed two different constructions. One uses as a building block a VCS with perfect reconstruction of black pixels while the other construction uses as a building block a binary secret sharing scheme. Subsequently, new constructions for visual cryptography with reversing have been described in [9, 14]. In particular, [9] considered the problem of minimizing the number of the shares held by each participant while in [14] the need of using as a building block a VCS with perfect reconstruction of black pixels is removed.

References

[1] G. Ateniese, C. Blundo, A. De Santis, and D. R. Stinson. Visual cryptography for general access structures. Information and Computation, 129((2):86–106, 1996.

[2] C. Blundo, P. D’Arco, A. De Santis, and D. R. Stinson. Contrast optimal threshold visual cryptography schemes. SIAM Journal on Discrete Mathematics, 16((2):224–261, 2003.

[3] C. Blundo, A. De Bonis, and A. De Santis. Improved schemes for visual cryptography. Designs, Codes, and Cryptography, 24:255–278, 2001.

[4] C. Blundo and A. De Santis. Visual cryptography schemes with perfect reconstruction of black pixels. Journal for Computers & Graphics, 22((4):449–455, 1998.

[5] C. Blundo, A. De Santis, and D. R. Stinson. On the contrast in visual cryptography schemes. Journal of Cryptology, 12((8):261–289, 1999.

[6] S. Cimato, A. De Santis, A. L. Ferrara, and B. Masucci. Ideal contrast visual cryptography schemes with reversing. Information Processing Letters, 93:199–206, 2005.

[7] A. De Bonis and A. De Santis. Randomness in secret sharing and visual cryptography schemes. Theoretical Computer Science, 314((3):351–374, 2004.

[8] T. Hofmeister, M. Krause, and H. U. Simon. Contrast-optimal k out of n secret sharing schemes in visual cryptography. Theoretical Computer Science, 240(2):471, 2000.

[9] C.M. Hu and W.G. Tzeng. Compatible ideal contrast visual cryptography schemes with reversing. In Proc. of ISC 2005, Lecture Notes in Computer Science, volume 3650, pages 300–313, 2005.

[10] M. Krause and H. U. Simon. Determining the optimal contrast for secret sharing schemes in visual cryptography. Combinatorics, Probability and Computing, 12((3):285–299, 2003.

[11] M. Naor and A. Shamir. Visual cryptography. In Proc. of Advances in Cryptology – EUROCRYPT ’94, Lecture Notes in Computer Science, volume 950, pages 1–12, 1995.

[12] E. R. Verheul and H. C. A. van Tilborg. Constructions and properties of k out of n visual secret sharing schemes. Designs, Codes, and Cryptography, 11(2):179, 1997.

[13] D. Q. Viet and K. Kurosawa. Almost ideal contrast visual cryptography with reversing. In Proc. of Topics in Cryptology - CT-RSA 2004, The Cryptographers’ Track at the RSA Conference 2004, Lecture Notes in Computer Science, volume 2964, pages 21–37, 2004.

[14] C.N. Yang, C.C. Wang, and T.S. Chen. Visual cryptography schemes with reversing. The Computer Journal, 51(6):710, 2008.

1Where white should really be interpreted as transparent. So we use white as a synonym for transparent.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for
9 Visual Cryptography Schemes with Reversing

9

Visual Cryptography Schemes with Reversing

CONTENTS

9.1 Introduction

9.2 Visual Cryptography Schemes

9.2.1 (k, k)-Threshold Visual Cryptography Schemes

9.2.2 Perfect Black Visual Cryptography Schemes

9.3 Almost Ideal Contrast VCS with Reversing

9.4 Ideal Contrast VCS with Reversing

9.4.1 A Construction Using a Binary Secret Sharing Scheme

9.4.2 Constructions Using Perfect Black VCSs

9.4.2.1 The Scheme by Cimato, De Santis, Ferrara, and Masucci

9.4.2.2 The Scheme by Hu and Tzeng

9.4.2.3 The Scheme by Yang, Wang, and Chen

9.4.2.4 Comparisons

9.4.3 A Construction Using a Nonperfect Black VCS

9.5 Conclusions

References

Table of Contents for 9 Visual Cryptography Schemes with Reversing

Create new playlist

Sign In

Sign Up

CONTENTS

Table of Contents for
9 Visual Cryptography Schemes with Reversing