14
Image Secret Sharing
WeiQi Yan, Jonathan Weir and Mohan S. Kankanhalli
Queen’s University Belfast, UK
National University of Singapore, Singapore
CONTENTS
14.1 Introduction
Cryptography plays a very vital enabling role in our modern computing infrastructure. Almost all real-world applications require keys (such as passwords) for the purposes of confidentiality, authentication, and nonrepudiation. The strength of such cryptographic applications is based on the secrecy of a key. Therefore, the loss of a key can lead to disastrous consequences. Thus, many cryptographers have tackled the following problem:
Suppose a secret s (a key) is divided into n > 1 parts (called secret shares) and it satisfies these properties:
The secret key s can be easily restored from k (k ≤ n) shares.
The secret key s cannot be restored from k − 1 (or less) shares.
The size of each share is not more than the size of the secret key s.
Such a scheme is referred to as a (k, n) threshold cryptography scheme or a secret sharing system[2][17]. It provides a backup mechanism to the secret key and it provides protection against the loss of a key. Secret sharing is also regarded as a mechanism to transfer secret information by public channels in cryptography [4]. Blakley based his secret sharing scheme on hyper-planes [17] and Shamir provided a solution based on the Lagrange interpolation [2]. Asmuth and Bloom scheme is based on the Chinese Remainder Theorem [5]. The details of these methods are available in [1] [12]. These traditional secret sharing schemes primarily concentrate on bit strings and do not take the specific content of these bits into account. However, with the increasing emphasis on security and digital rights management of multimedia data, the connection between multimedia and cryptography is becoming stronger. In this context, we present our novel ideas on color image sharing in which we utilize the concept of secret sharing from cryptography and employ it to protect a secret color image. As we shall see, the ideas cannot be directly applied so we need to take into account that the data under consideration describes color images and is not any generic bit stream. In our scheme, a secret color image is divided into n shares. Each share is an innocuous image totally unrelated to the secret image. We utilize k (or more) shares in order to perfectly reconstruct the secret image. However, having access to k − 1 (or less) shares will not reveal the secret color image.
We envisage several useful applications for a color image sharing scheme. Suppose we have a secret color image that we desire to protect. If we employ traditional cryptographic techniques, then we need to encrypt the image and store the image on a secure server. We then need to pay attention on the security of the key used for encryption. This server would then become a single focus of attack from a potential adversary. However, with an image sharing scheme, we can divide the information in the image into several shares and keep them on separate servers. This would allow for a lot more redundancy in the protection since breaking one server will not reveal the secret image. Another application would be that of data hiding. Suppose we would like to transmit a secret image over a noisy and insecure channel. We could divide the image information into several shares that are basically innocuous images. These images could be transmitted and at the other end, the secret image could be reconstructed from the threshold number of shares. Another useful application would be that of a military command and control system based on the Clark-Wilson security model [11]. Suppose we want the battlefield plans to be made only if k out of n commanders agree. In which case, we could divide the battle terrain map into n shares and distribute it to the commanders. Only if k of them get together can they restore the terrain map and agree to a battle plan. In general, our scheme would be advantageous in any situation where a group of mutually suspicious individuals or processes need to cooperate and every threshold subset of the group needs to be given the veto power.
The problem of color image sharing is formally defined as follows. In order to transfer a color image I through a public channel securely, the information of the color image is divided into n pieces and embedded into images Ii, (i = 1, 2, ⋯, n), and we call the images Ii, (i = 1, 2, ⋯ , n) as shares. With the knowledge of any k(k < n) shares Ii, (i =1, 2, ⋯ ,k), the restoration of the original color I image is easy; with the knowledge of any k − 1(k < n) shares, the restoration of the original image I is impossible (i.e., any image is equally likely to be reconstructed).
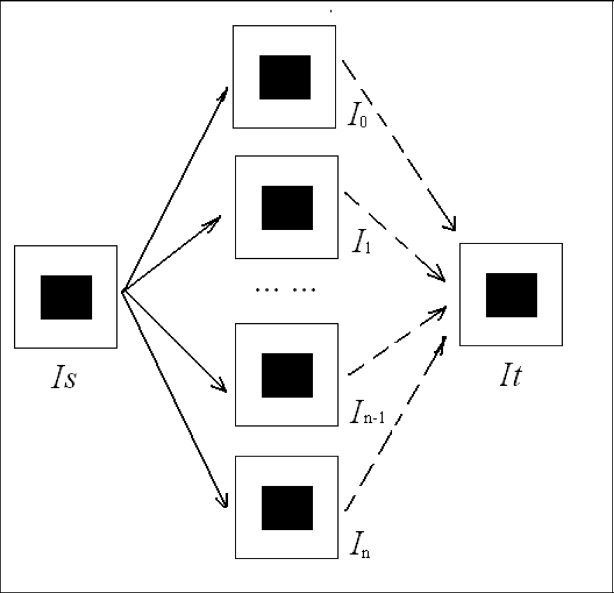
FIGURE 14.1
Principle of image sharing.
In Figure 14.1, the left-most image is the original color image that we desire to keep as a secret and it is divided into several blocks (subimages). We process each of these blocks into n shares in order to create the subimages shares. If required, we can compose these shares Ii, (i, = 1, 2, ⋯ , n) together and compute the blocks in the right-most image. Block-based processing is done for breaking correlation. Note that our scheme will require a minimum of k shares in order for Ir to be exactly equal to Is. If less than k shares are used, then Is cannot be restored. The threshold is indispensable in color image sharing.
14.2 State of the Art
Applying visual cryptography techniques to color images is a very important area of research because it allows the use of natural color images to secure some types of information. Due to the nature of a color image, this again helps to reduce the risk of alerting someone to the fact that information is hidden within it. It should also allow high quality sharing of these color images. Color images are also highly popular and have a wider range of uses when compared to other image types. Many of the techniques presented within this section use halftone technologies on the color images in order to make them work with visual cryptography. That is why color visual cryptography is presented within this section.
In 1996, Naor and Shamir published a second article on visual cryptography ”Visual Cryptography II: Improving the Contrast via the Cover Base” [23]. The new model contains several important changes from their previous work; they use two opaque colors and a completely transparent one.
The first difference is the order in which the transparencies are stacked. There must be an order to correctly recover the secret. Therefore, each of the shares needs to be predetermined and recorded so recovery is possible. The second change is that each participant has c sheets, rather than a single transparency. Each sheet contains red, yellow, and transparent pixels. The reconstruction is done by merging the sheets of participant I and participant II, i.e., put the i-th sheet of II on top of the i-th sheet of I and the (i + 1)-th of I on top of the i-th of II.
The two construction methods are monochromatic construction and bichromatic construction. In the monochromatic construction, each pixel in the original image is mapped into c subpixels and each participant holds c sheets. In each of participant I sheets, one of the subpixels is red and the remaining c − 1 subpixels are transparent. In each of participant II sheets, one of the subpixels is yellow, the other c − 1 subpixels are transparent. The way the sheets of participant I and II are merged is by starting from the sheet number 1 of participant I, then putting sheet number 2 of participant II on top of it, then sheet number 2 of participant I on top of that, and so on.
The order in which subpixels of participant I are colored red constitutes a permutation π on {1, ⋯ , c} and the order which the subpixels of participant II are colored yellow constitutes a permutation σ. π and σ are generated as follows: π is chosen uniformly at random from the set of all permutations on c’s elements. If the original pixel is yellow, then π = σ, therefore each red subpixel of the i-th sheet of participant I will be covered by a yellow subpixel of the same position of the i-th sheet of participant II. If the original pixel is red, then σ(i) = π(i + 1) for 1 ≤ i ≤ c − 1 and σ(c) = π(1), therefore each yellow subpixel of the i-th sheet of participant II will be covered by a red subpixel of the same position of the (i + 1)-th sheet of participant I except the c-th sheet. In practice, the first sheet of participant I is not necessarily stored since it is always covered by other sheets.
A very primitive example of color image sharing appeared in [24]. In this example, each pixel of the color secret image is expanded to a block of 2 × 2 subpixels. Each one of these blocks is filled with red, green, blue, and white (transparent) colors, respectively. Taking symmetries into account, 24 different possibilities for the combination of two pixels can be obtained. It is claimed that if the subpixels are small enough, the human visual system will average out the different possible combinations to 24 different colors. To encrypt a pixel of the colored image, round the color value of that pixel to the nearest representable color. Select a random order for the subpixels on the first share and select the ordering on the second share such that the combination produces the required color.
The advantage of this scheme is that it can represent 24 colors with a resolution reduction of 4, instead of 242 = 576. The disadvantage is that the 24 colors are fixed once the basic set of subpixel colors is fixed.
Another primitive scheme was also presented [29] and extended more recently [34]. Verheul and Van Tilborg’s scheme provides a c-color (k, n)-threshold scheme. This scheme uses the black pixel to superimpose on the result of two color pixels, superimposition, if they give a resultant color that is not in the original color palette. This can be achieved by making sure the superimposed color pixels result in a noncolor palette color, one of which is changed to a black pixel or by ensuring that one of the color pixels is changed to black before the superimposing operation [10]. Yang and Laih improve on the pixel expansion aspect of the Verheul and Van Tilborg scheme and their (n, n)-threshold scheme is optimal since they match the following lower bound placed on pixel expansion, formulated in [10]:
Hou et al. [18] proposed a novel approach to share color images based on halftoning. With this halftone technology, different gray levels can be simulated simply by altering the density of the printed dots. Within bright parts of the image the density is sparse, while in the darker parts of the image, it is dense. This is very helpful in the visual cryptography sense because it is able to transform a gray-scale image into a black and white image. This allows for traditional visual cryptography techniques to be applied. Similarly, the color decomposition method is used for color images, which also allows the proposed scheme to retain all the advantages of traditional visual cryptography, such as no computer participation required for the decryption/recovery of the secret.
Hou himself also provided one of the first color decomposition techniques to generate visual cryptograms for color images [19]. Using this color decomposition, every color within the image can be decomposed into one of three primary colors: cyan, magenta, or yellow. This proposal is similar to traditional visual cryptography with respect to the pixel expansion that occurs. One pixel is expanded into a 2 × 2 block where two color pixels are stored along with two transparent (white) pixels.
However, [21] examined the security of Hou’s [19] scheme, and while the scheme is secure for a few specific two-color secret images, the security cannot be guaranteed for many other cases.
Improving this pixel expansion and also working out the optimal contrast of color visual cryptography schemes have been investigated [10]. In the paper, they prove that contrast-optimal schemes are available for color visual cryptography (VC) and then further go on to prove the optimality with regard to pixel expansion.
A lossless recovery scheme outlined by [20] considers halftoning techniques for the recovery of color images within visual cryptography. The scheme generates high quality halftone shares that provide lossless recovery of the secrets and reduces the overall noise in the shares without any computational complexity. Their proposed method starts by splitting the color channels into its constituent parts, cyan (C), magenta (M), and yellow (Y). Each channel has grayscale halftoning applied to it. Error diffusion techniques discussed in [35] are then applied to each halftone channel. A circularly symmetric filter is used along with a Gaussian filter. This provides an adequate structure for the dot placement when constructing the shares.
Efficiency within color visual cryptography [25] is also considered which improves on the work done by [34, 3]. The proposed scheme follows Yang and Laih’s color model. The model considers the human visual system’s effect on color combinations out of a set of color subpixels. This means that the set of stacked color subpixels would look like a specific color in original secret image. As with many other visual cryptography schemes, pixel expansion is an issue. However Shyu’s scheme has a pixel expansion of ⌈log2c⌉, which is superior to many other color visual cryptography schemes especially when c, the number of colors in the secret image becomes large. An area for improvement however would be in the examination of the difference between the reconstructed color pixels and the original secret pixels. Having high quality color VC shares would further improve on the current schemes examined within this survey, this includes adding a lot of potential for visual authentication and identification.
Chang et al. [6] present a scheme based on smaller shadow images, which allows color image reconstruction when any authorized k shadow images are stacked together using their proposed revealing process. This improves on the following work [32], which presents a scheme that reduces the shadow size by half. Chang et al.’s technique improves on the size of the share in that, as more shares are generated for sharing purposes, the overall size of those shares decreases.
In contrast to color decomposition, Yang and Chen [33] propose an additive color mixing scheme based on probabilities. This allows for a fixed pixel expansion and improves on previous color secret sharing schemes. One problem with this scheme is that the overall contrast is reduced when the secrets are revealed.
In most color visual cryptography schemes, when the shares are superimposed and the secret is recovered, the color image gets darker. This is due to the fact that when two pixels of the same color are superimposed, the resultant pixel gets darker. Cimato et al. [9] examine this color darkening by proposing a scheme that has to guarantee that the reconstructed secret pixel has the exact same color as the original. Optimal contrast is also achieved as part of their scheme. This scheme differs from other color schemes in that it considers only 3 colors when superimposing, black, white, or one pixel of a given color. This allows for perfect reconstruction of a color pixel, because no darkening occurs, either by adding a black pixel or by superimposing two colors that are identical, that ultimately results in a final darker color.
A technique that enables visual cryptography to be used on color and grayscale images is developed in progressive color visual cryptography [13]. Many current state-of-the-art visual cryptography techniques lead to the degradation in the quality of the decoded images, which makes it unsuitable for digital media (image, video) sharing and protection. In [13], a series of visual cryptography schemes have been proposed that not only support gray-scale and color images, but also allow high quality images including that of perfect (original) quality to be reconstructed.
The annoying presence of the loss of contrast makes traditional visual cryptography schemes practical only when quality is not an issue which is relatively rare. Therefore, the basic scheme is extended to allow visual cryptography to be directly applied on grayscale and color images. Image halftoning is employed in order to transform the original image from the grayscale or color space into the monochrome space which has proved to be quite effective. To further improve the quality, artifacts introduced in the process of halftoning have been reduced by inverse halftoning.
With the use of halftoning and a novel microblock encoding scheme, the technique has a unique flexibility that enables a single encryption of a color image but enables three types of decryptions on the same ciphertext. The three different types of decryptions enable the recovery of the image of varying qualities. The physical transparency stacking type of decryption enables the recovery of the traditional VC quality image. An enhanced stacking technique enables the decryption into a halftone quality image. A progressive mechanism is established to share color images at multiple resolutions. Shares are extracted from each resolution layer to construct a hierarchical structure; the images of different resolutions can then be restored by stacking the different shared images together.
The advantage is that this scheme allows for a single encryption, multiple decryptions paradigm. In the scheme, secret images are encrypted/shared once, and later, based on the shares, they can be decrypted/reconstructed in a plurality of ways. Images of different qualities can be extracted, depending on the need for quality as well as the computational resources available. For instance, images with loss of contrast are reconstructed by merely stacking the shares; a simple yet effective bit-wise operation can be applied to restore the halftone image; or images of perfect quality can be restored with the aid of the auxiliary look-up table. Visual cryptography has been extended to allow for multiple resolutions in terms of image quality. Different versions of the original image of different qualities can be reconstructed by selectively merging the shares. Not only this, a spatial multiresolution scheme has been developed in which images of increasing spatial resolutions can be obtained as more and more shares are employed.
This idea of progressive visual cryptography has recently been extended [14] by generating friendly shares that carry meaningful information and that also allows decryption without any computation at all. Purely stacking the shares reveals the secret. Unlike [13] and [7] which require computation to fully reconstruct the secret, the scheme proposed in [15] has two types of secrets, stacking the transparencies reveals the first, but computation is again required to recover the second-level secret. Fang’s scheme is also better than the polynomial sharing method proposed in [26] by Thien and Lin. The method proposed in [26] is only suitable for digital systems and the computational complexity for encryption and decryption is also a lot higher.
Currently, one of the most robust ways to hide a secret within an image is by typically employing visual cryptography. The perfect scheme is extremely practical and can reveal secrets without computer participation. Recent state-of-the-art watermarking [8] can hide a watermark in documents that require no specific key in order to retrieve it. We take the idea of unseen visible watermarks and apply a secure mask to them and incorporate it for use within the VC domain, thus improving the overall security that is currently one of its weaknesses.
Weir et al. [31] also provide a mechanism for secret sharing using color images as a base. The technique relies on visual cryptography as a mechanism for sharing the secret. Many smaller secrets can be embedded within a color image and a final share can be created in order to reveal all of the secrets. The color image is visually similar to the original image before embedding due to the high Peak-Signal-to-Noise Ratio (PSNR) achieved after embedding.
Another recent novel application for color image sharing and using color images for secret sharing was presented by Weir and Yan [30]. Using Google Maps, along with its Street View implementation, personally identifiable information can be obscured using visual cryptography techniques and can be accurately recovered by authorized individuals who may need the information. Specifically for law enforcement agencies who many find this type of information helpful for a particular case. This type of practical application is very important for the progression of visual cryptography, which presents a unique way of using these techniques in a real-world situation.
14.3 Approaches for Image Sharing
14.3.1 Shamir’s Secret Sharing Scheme
Shamir’s secret sharing scheme is based on the Lagrange interpolation [2]. Given a set of points (xi,yi)(i = 0,1, 2, …, k), the Lagrange interpolation polynomial Lk (x) can be constructed using:
Given a secret, it can be easily shared using this interpolation scheme. If GF(q) denotes a Galois field (q > n), the following polynomial is constructed by choosing proper coefficients a0, a1, ⋯•, ak from GF(q), which satisfy:
where s* is the secret key. The coefficients are randomly chosen over the integers [0, q) and the details are provided in [2]. Suppose si = f (ai),(i = 0,1, ⋯ , k), each Si is known as a share and they all can be delivered to different persons.
Now we would like to reconstruct the original secret. Suppose k people have provided their shares si, (i = 0, 1, ⋯ , k). The following Lagrange interpolation polynomial is utilized to reconstruct the original secret:
where addition, subtraction, multiplication, and division are defined over GF(q).
14.3.2 Color Image Sharing Based on the Lagrange Interpolation
When an image is treated as a secret, we can share the secret based on the Lagrange interpolation. We consider the image to be a matrix; and Lagrange interpolation is generalized for matrices.
We assume a grayscale image corresponds to a matrix A. Given matrix , where w and h are integer (w = 1, 2, ⋯ ,W; h = 1, 2, ⋯ , H; i = 0,1, ⋯ , k), k is the number of shares. We define the matrix operations of Lagrange polynomials with degree k in the Galois field:
where (xi, Ai) is the feature point, Ai( (i = 0,1, ⋯ ,k)) are matrices of size W × H, the elements being nonnegative, xi is a real number and xi < xj (i ≤ j).
Our novel idea for color image sharing using Lagrange interpolation is the following. We utilize the secret image and a few ( < n) other chosen innocuous images to build the Lagrange interpolation polynomial. We then construct new images based on this interpolation to obtain a total of n images. We now can use all the innocuous images and the new reconstructed images as the shares of the secret image. And the secret image is not distributed but it can be always reconstructed using the requisite number of shares. So our novelty is in the construction of new shares based on the secret image and some chosen innocuous images. We now provide the details of the scheme. In Figure 14.2, assume that the secret image that we desire to share is at the position x = 0.

FIGURE 14.2
Image sharing based on the Lagrange interpolation in (a) and (b).
In Figure 14.2(a), we position an innocuous image at x2. We can now compute many new shares with the parameters in the interval (x2 − d, x2 + d), d > 0, (we have used ). Without loss of generality, we select the parameter at the position x1 as our newly created share (based on 0 and x2). We now consider the images at x2 and x1 as the shares of the secret image at 0. For the reconstruction of the secret, we can collect the two shares, we calculate the coefficients of Lagrange interpolation polynomial first and then compute the image at position 0. In Figure 14.2(b), we put the shares in x1, x2 and obtain the secret color image at 0; and in Figure 14.2(b), we put the shares at x1, x2, x3 and restore the secret image at position 0. For a color image, this operation can be performed for each color channel. Figure 14.3 shows our experimental results for the Lagrange interpolation scheme of a color image.

FIGURE 14.3
Experimental results of image sharing based on the Lagrange interpolation in (a) and (b).
In Figure 14.3(a), the original color image is the secret image to be shared, at least two shares are needed to reconstruct the original image, i.e., it is a (2, n) scheme, thus k = 2. Thus, share 2 has been generated using the original color image and share 1 (which is an innocuous image). Now, share 1 and share 2 can be distributed independently and the original color image can be reconstructed anytime if we obtain both the shares. In Figure 14.3(b), the original color image is the secret color image and at least three shares are required to restore the secret color image. This is because k = 3, therefore it is a (3, n) secret image sharing scheme. Notice that the secret image is somewhat visible in the generated shares. We will fix this problem later with the block-based approach.
However, the Lagrange polynomial based image sharing has a potential practical problem. It cannot yield too many shares. This is because the Lagrange polynomial curve with a high degree has severe oscillations once the degree of the polynomial is greater than nine [16]. The consequence of this oscillations phenomenon is that it is impossible to constrain the pixel values to lie between 0 and 255. As a result, the resultant shares are not proper images anymore as shown in Figure 14.4.

FIGURE 14.4
The image sharing by using a high degree polynomial interpolation in (a)-(c).
In Figure 14.4, the resultant image Figure 14.4(a) is the original secret image, Figure 14.4(b) is the innocuous image and Figure 14.4(c) is the generated share while the rest of the shares are all-white images. We use a polynomial of degree 8 for generating Figure 14.4(c). Figure 14.4(c) has obvious color overflow problems because some pixel values are more than 255 and some are less than zero, hence the image quality is severely degraded. Note that this is not a problem in Shamir’s original secret sharing scheme because they consider the secret to be shared as a binary integer, and thus a share can take on any value. In our case, this binary integer has some constraints because they denote image pixel values. In order to overcome this serious limitation, it is obvious that some form of a piece-wise polynomial interpolation is required in order to bound the degree of the polynomial and thus constrain the oscillations. We have developed a new color image sharing scheme based on moving lines, which is a rational implicit curve.
14.3.3 Color Image Sharing Based on Moving Lines
It is well known that the equation of a line in the homogenous form in pro-jective geometry [22] is:
where a, b, and c are not all zero, (X, Y, W) are the homogenous coordinates of points whose Cartesian coordinates are:
It is obvious that X, Y, W cannot all be zero. Let P denote the triple (X, Y, W) and L denote the triple ( a, b, c). We refer to the line L that is:
Thus, we can see that a point P lies on a line L = (a, b, c) only and if only P • L = 0 , where P • L is the dot product.
Now we consider the line L containing two points P1 = (X1, Y1, W1) and P2 = (X2,Y2,W2), and also the point P at which two lines L1 = (a1,b1,c1) and L2 = (a2, b2, c2) intersect. Because of the duality principle (of points and lines), we have these cross products:
A homogeneous point whose coordinates are functions of a variable t (i.e., it is parameterized by a variable t) is denoted as:
which actually is the rational curve:
If the functions are of the following form:
With being a given set of blending function, then equation (14.11) defines a curve:
where the homogeneous points are Pi = (Xi, Yi, Wi). Likewise,
denotes the family of lines a[t]x + b[t]y + c[t] =0.
In order to obtain the intersection of two pencils, we notice the following four lines L0,0, L0,1, L1,0, and L1,1 from which two pencils are defined:
The points, at which they intersect for parameter values t = 0, ∆t, 2∆t, ⋯ , 1 are on a curve. The parameter t = 0, ∆t, 2∆t, ⋯ , 1 is adaptively given and it may take any real number value in the interval [0,1] for a piece of curve and it also can be extended to the infinite interval [−∞, +∞] for the whole curve. The curve turns out to be a conic section, which can be expressed as a rational Bernstein–Bezier curve P[t] as follows:
It is clear that P[t] is a quadratic rational Bezier curve [27][28] whose control points are:
The graph of a quadratic curve generated by moving lines is shown in Figure 14.5(a).

FIGURE 14.5
Intersection of two pencils of lines in (a) and (b).
In general, the curve comprising of L0,0, L0,1, L0,2, and L1,0,L1,1 is:
then P[t] = L0[t] × L1[t], t ∈ [0,1] is a cubic rational Bezier curve [16].
Without loss of generality, the moving lines consisting of L0,0,L0,1, ⋯•,L0,p, and L1,0, L1,1, ⋯, L1,q are:
then P[t] = L0[t] × L1[t], t ∈ [0,1] represents a rational Bezier curve of degree p + q as shown in Figure 14.5(b) [16].
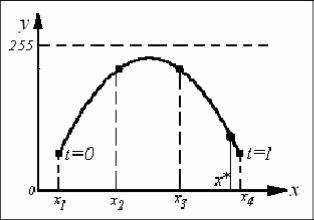
FIGURE 14.6
Image sharing scheme based on moving lines.
As in the case of Lagrange interpolation, we now construct the scheme of image sharing based on moving lines as shown in Figure 14.6. In Figure 14.6, the x-coordinate depicts the given position of the original secret color image, the y-coordinate indicates the values of the gray-scale pixel value, t is the parameter for moving lines generation, and x* is the position of the new computed share. For image sharing, we compute the shares using the above implicit curve. We now present the detailed steps for our moving lines based on the color image sharing scheme.
Steps of sharing a color image:
Suppose we are given one secret image I0 to be shared, k + 1 images I0, I1, ⋯ , Ik as the innocuous images and a group of corresponding parameters x0, x1, ⋯ , xk (x0 ≤ x1 ≤ ⋯ ≤ xk) as input;
Calculate an arbitrary new share corresponding to a parameter within the interval of the given parameters (x1,xk);
The images (greater than k) I0, I1, ⋯•, Ii−1, Ip, Ii,Ii+1,⋯, Ik; 0 ≤ i − 1 ≤ p ≤ i ≤ k and their corresponding parameters x0, x1, ⋯, xi−1, xp, xi, xi+1, ⋯, xk (x0 ≤ x1 ≤ ⋯ ≤ xi−1 ≤ xp ≤ xi ≤ xi+1 ≤ ⋯ ≤ xk) are the output computed image shares.
Steps of reconstructing the color image:
Select k image shares I0, I1, ⋯•, Ik and their corresponding position parameters x0, x1, ⋯•, xk (x0 ≤ x1 ≤ ⋯ ≤ xk) and the position parameter of the color image x0 as the input;
Calculate the implicit curve corresponding to pixels in each share according to the moving lines scheme P[t] = L0[t] × L1[t], t ∈ [0,1];
Reconstruct the secret color image by the scheme of moving lines at the position of x0 as output.
Note that each of the steps has to be applied separately for each color channel. The use of a rational curve has several advantages, such as it does not have the oscillations phenomenon of polynomials with a high degree; a rational curve is easy to be controlled and is able to express conic curves. Also a polynomial curve with a high degree cannot guarantee that the interpolation values can be constrained to a given range [16]. Thus, when a rational curve is employed to share a color image, the scheme based on moving lines yields more shares than that of the one based on the Lagrange interpolating polynomial. With more shares, the secret color image can be shared in a more secure manner with greater flexibility. However, this greater flexibility comes at an increased cost of computation compared to that of the Lagrange interpolations scheme.
14.3.4 Improved Algorithm
If we carefully examine Figure 14.3, we can see that the profile of the secret image is visible in the constructed image shares. The reason is that the correlation of the secret image is not broken during the image sharing process. So far, we selected only one X-position parameter for the secret image, thus only one share (i.e., the newly created one) is closely related to the secret image and the other shares are totally independent. Thus, the innocuous images do not contribute towards image hiding. We now modify the earlier approach slightly to make all the shares involved in data hiding by utilizing a block-based approach with multiple parameters:
Steps of block-based image sharing:
Divide the secret image into blocks.
Designate different parameters (i.e., different innocuous image position) for each block.
Share the secret image using the earlier approach.
Write down the parameters and positions embedded in the corresponding shares of each block for secret restoration.
The restoration handling is the inverse procedure of the encoding procedure.
In order to clearly explain the scheme, we illustrate the improved approach in Figure 14.7. In Figure 14.7, the secret image is divided into four blocks, each block is embedded into the given innocuous image share at a different spatial position. The secret image can be reconstructed by applying the scheme block-wise again. This method effectively breaks the correlation of the original secret image with the secret image being divided into many blocks and these blocks being hidden in different shares at different locations. Thus, the secret image is no longer visible in the shares.

FIGURE 397.14
Improved algorithm of image sharing.
14.4 Experiment and Evaluation
Both of the algorithms proposed in this chapter can theoretically be employed for image sharing, but actually they are different in terms of practical implementation. Color image sharing based on Lagrange interpolation allows for only a limited number of shares due to the oscillations phenomenon. Color image sharing based on moving lines can theoretically generate an unlimited number of shares. In practice, generating more shares will require more computation. Thus, as a trade-off, we usually share a color image into at most five shares.

FIGURE 14.8
The experimental results of image sharing by moving lines.
We now present some experimental results on images of size 128× 128. The shares and original secret image based on quadric curves of moving lines are shown in Figure 14.8, which is a (2, n) sharing example. In Figure 14.9, we illustrate a (3, n) scheme based on cubic curves of moving lines.

FIGURE 14.9
The experimental results of image sharing by moving lines.

FIGURE 14.10
The experimental results of image sharing by moving lines.
Figure 14.9 is the result of (3, n) scheme based upon moving lines to share a given original image, with share 1 and share 2 being innocuous. Share 3 is the new computed share. By using shares 1, 2, 3, and their parameters, the original color image can be restored.
Figure 14.10 is the result of a (4, n) scheme based on a moving line to share a color image by given original secret image, share 1, share 2, and share 3. Share 4 is the new computed share. When shares 1, 2, 3, 4, and their parameters are used for the moving lines based scheme, the original color image can be perfectly restored.
For a sensitive application, it is better to compute the shares by performing block-by-block (e.g., 8 × 8 pixel blocks) processing. The advantage of such an approach is that distributing the reconstructed blocks into the various innocuous images can break the correlation of the secret image in the image share. Thus, instead of taking n − 1 innocuous images and creating the n-th share (which can possibly reveal some correlations), we can take n innocuous images and distribute the secret image blocks within them. In fact, the secret color images need not be of the same size as that of the shares. Actually, if the shares have a larger size, the hiding of the color image will be more secure.
Figure 14.11 shows an example of breaking the correlation between neighboring blocks of the secret image. In this (4, n) image sharing scheme, we have divided the original image into four equal-sized rectangular blocks and have shared these blocks using a quadric curve generated by the moving lines technique. What is different here from the earlier examples (where we created a whole new image as a share) is that we embed the information of each rectangular block into one of the image shares. The embedded information of share 1 is in the lower-left corner, that of share 2 is in the upper-left position while that of share 3 is embedded is in the upper-right region, and that of share 4 is in the lower-right corner. Thus, the information of the original secret image is shared among all the image shares. While this example is a simple illustration of how the correlation can be broken, it is clear that more sophisticated secret image subdivision and sharing schemes can be devised using the same principle.

FIGURE 14.11
Breaking the correlation of neighboring blocks in an image.
14.5 Conclusion
In this chapter, we introduce the novel concept of color image sharing based on Lagrange interpolation and moving lines. The security of secret sharing is built upon the computation of polynomials. Given enough shares, the coefficients of the interpolating polynomial can be exactly determined. However, if an attacker does not possess the threshold number of shares and the image shares, he will not be able to reconstruct the polynomial. Thus, he will not able to restore the secret image properly.
Secret sharing based on Lagrange interpolation is often utilized to share binary strings, but it is difficult to use for color image sharing since it yields only a limited number of shares. We therefore have developed a new color image sharing scheme based on moving lines that does not have that limitation. An implicit curve generated by moving lines is a rational curve; we believe it can therefore be directly applied for sharing compressed-domain images.
Our future work will focus on further investigation of color image sharing in the compressed domain. The possible research directions in the future are:
Color image sharing based on compressed domain processing. Ideas related to DCT, DFT, and DWT can be employed in color image sharing.
Color image sharing based on visual cryptography. If visual cryptography could be implemented in color images, we could share color images with visual cryptography. Since visual cryptography is perfectly secure, color image sharing based on visual cryptography will be extremely robust.
Bibliography
[1] A. Salomaa. Public-Key cryptography. Springer, Berlin Heidelberg, 1990.
[2] A. Shamir. How to share a secret. Communications of the ACM, 22((11):612–613, 1979.
[3] C. Blundo, A. De Bonis, and A. De Santis. Improved schemes for visual cryptography. Designs, Codes and Cryptography, 24((3):255–278, 2001.
[4] C. Liu. Introduction to combinatorial mathematics. McGraw-Hill, New York, 1968.
[5] C.A. Asmuth and J. Bloom. A modular approach to key safeguarding. IEEE Transactions on Information Theory, 29:208–210, 1983.
[6] C.C. Chang, C.C. Lin, C.H. Lin, and Y.H. Chen. A novel secret image sharing scheme in color images using small shadow images. Information Sciences, 178((11):2433–2447, 2008.
[7] S.K. Chen and J.C. Lin. Fault-tolerant and progressive transmission of images. Pattern Recognition, 38((12):2466–2471, 2005.
[8] S.C. Chuang, C.H. Huang, and J.L. Wu. Unseen visible watermarking. In ICIP (3), pages 261–264, 2007.
[9] S. Cimato, R. De Prisco, and A. De Santis. Colored visual cryptography without color darkening. Theoretical Computer Science, 374(1–3):261–276, 2007.
[10] S. Cimato, R. De Prisco, and A. De Santis. Optimal colored threshold visual cryptography schemes. Designs, Codes and Cryptography, 35((3):311–335, 2005.
[11] D. Gollmann. Computer Security. John Wiley & Sons, Chichester, 1999.
[12] D.E. Denning. Cryptography and data security. Addison-Wesley, London, 1982.
[13] J. Duo, W.Q. Yan, and M. S. Kankanhalli. Progressive color visual cryptography. SPIE Journal of Electronic Imaging, 14(3), 2005.
[14] W.P. Fang. Friendly progressive visual secret sharing. Pattern Recognition, 41((4):1410–1414, 2008.
[15] W.P. Fang and J.C. Lin. Visual cryptography with extra ability of hiding confidential data. Journal of Electronic Imaging, 15(2):023020, 2006.
[16] G. Farin. Curves and Surfaces for Computer aided Geometric Design: A Practical Guide (3rd Edition). Academic Press, Boston, USA, 1992.
[17] G.R. Blakley. Safeguarding cryptographic keys. In Proc. of AFIPS 1979 National Computer Conference, volume 48, pages 313–317, Aelington, 1979.
[18] Y.C. Hou, C.Y. Chang, and S.F. Tu. Visual cryptography for color images based on halftone technology. In Proceedings of the 5th World Multiconference on Systemics, Cybernetics, and Informatics (SCI 2001), Orlando, FL, Vol. XIII, pp. 441–445.
[19] Y.C. Hou. Visual cryptography for color images. Pattern Recognition, 36:1619–1629, 2003.
[20] N. K. Prakash and S. Govindaraju. Visual secret sharing schemes for color images using halftoning. In Proceedings of Computational Intelligence and Multimedia Applications, 3:174–178, December 2007.
[21] B.W. Leung, F.Y. Ng, and D.S. Wong. On the security of a visual cryptography scheme for color images. Pattern Recognition, 2008, 42(5):929–940 (2009).
[22] M.A. Penna and R.R. Patterson. Projective Geometry and Its Applications to Computer Graphics. Prentice Hall, New Jersey, 1986.
[23] M. Naor and A. Shamir. Visual cryptography II: Improving the contrast via the cover base. In Proceedings of the International Workshop on Security Protocols, pages 197–202, London, UK, 1997. Springer-Verlag.
[24] V. Rijmen and B. Preneel. Efficient color visual encryption for shared colors of benetton. EUCRYPTO ’96, 1996.
[25] S. J. Shyu. Efficient visual secret sharing scheme for color images. Pattern Recognition, 39((5):866–880, 2006.
[26] C.C. Thien and J.C. Lin. An image-sharing method with user-friendly shadow images. IEEE Transactions on Circuits and Systems for Video Technology, 13((12):1161–1169, 2003.
[27] T.W. Sederberg and F.L. Chen Implicitization using moving curves and surfaces. In Proceedings of SIGGRAPH’95, pages 301–308, Los Angeles, 1995. ACM Press.
[28] T.W. Sederberg, T. Saito, D.X. Qi, and K.S. Klimaszewski. Curve im-plicitization using moving lines. Computer Aided Geometric Design, (11):687–706, 1994.
[29] E.R. Verheul and H.C.A. Van Tilborg. Constructions and properties of k out of n visual secret sharing schemes. Des. Codes Cryptography, 11((2):179–196, 1997.
[30] J. Weir and W. Yan. Resolution variant visual cryptography for street view of Google maps. In IEEE International Symposium on Circuits and Systems, 2010. ISCAS 2010, May 2010.
[31] J. Weir, W.Q. Yan, and D. Crookes. Secure mask for color image hiding. In Third International Conference on Communications and Networking in China, 2008. China Com 2008, pages 1304–1307, Aug. 2008.
[32] C.N. Yang and T.S. Chen. New size-reduced visual secret sharing schemes with half reduction of shadow size. In ICCSA (1), pages 19–28, 2005.
[33] C.N. Yang and T.S. Chen. Colored visual cryptography scheme based on additive color mixing. Pattern Recognition, 41((10):3114–3129, 2008.
[34] C.N. Yang and C.S. Laih. New colored visual secret sharing schemes. Designs, Codes and Cryptography, 20((3):325–336, 2000.
[35] Z. Zhou, G. R. Arce, and G. Di Crescenzo. Halftone visual cryptography. IEEE Transactions on Image Processing, 15((8):2441–2453, 2006.
