5 Probabilistic Visual Cryptography Schemes

Visual cryptography schemes allow the encoding of a secret image, consisting of black or white pixels, into n shares that are distributed to the set P $P$ of n participants. The shares are such that only qualified subsets of participants can “visually” recover the secret image. The secret pixels are shared with techniques based on subdividing each secret pixel into a certain number m, m ≥; 2 of subpixels. Such a parameter m is called the pixel expansion, since the reconstructed shared image becomes m times bigger than the original. This cryptographic paradigm was introduced by Naor and Shamir [16]. They analyzed the case of (k, n)-threshold visual cryptography schemes, in which a black and white secret image is visible if and only if any k transparencies are stacked together.

The pixel expansion has a number of drawbacks, affecting the quality of the reconstructed image and the complexity of the visual cryptography scheme (VCS). In some cases, the pixel expansion is exponential, and this limits the applicability of the VCS. In general, the “quality” of the reconstructed image depends both on the pixel expansion and on the contrast, which is another measure of the goodness of the scheme. A number of papers studying the best pixel expansion and the best contrast have appeared in the literature. A partial list of such papers include [2, 4, 5, 6, 7, 12, 14, 15]. Some other papers have focused on different models or properties. For example, in [1], visual cryptography schemes for general access structures (where the qualified set of participants are arbitrary and not defined by a threshold of participants) have been studied. Schemes where the shares show meaningful pictures (not related to the secret) are studied in [3]. In [24] the problem of not distorting the original image is considered. Some research has also considered the case of colored images (see for example [10, 9, 19, 25]).

To deal with the pixel expansion, Yang [22, 23] has introduced a new model of visual cryptography in which the reconstruction of the secret image is probabilistic, but the shares have the same size of the secret image, i.e., the schemes have no pixel expansion. To be fair, a first attempt to provide VCS without pixel expansion has been done by Ito et al. in [13]. In both Ito and Yang models, each pixel is reconstructed “OR”ng the corresponding single pixel contained in the shares. Such models are called probabilistic, because they give no absolute guarantee on the correct reconstruction of the original pixel: in some cases, the reconstructed pixel is wrong. This differs from the traditional VCS, which are now called deterministic, where the reconstruction of an “approximation” of the secret pixel is guaranteed. Here the approximation means that a white (black) pixel can be, in some cases, replaced in the reconstructed image by a set of subpixels having a given set of whiteness (blackness). Since in probabilistic models the secret pixel is correctly reconstructed with some probability, the quality of the reconstructed images depends on how big is the probability of correctly reconstructing the secret pixels.

Between deterministic schemes and probabilistic schemes it is possible to set a trade-off. In a deterministic scheme a certain pixel expansion is paid for the guarantee of a correct reconstruction. In a probabilistic scheme a reconstruction with no pixel expansion is paid with a (small) probability of making mistakes in reconstructing the secret image. In some cases it is possible to sacrifice some pixel expansion in order to improve the probabilistic reconstruction of the secret image or vice versa. Yang’s model has been generalized in Cimato et al. [11] showing how it is possible to trade pixel expansion for the probability of a good reconstruction. Such a model can be seen as a generalization of both the classical deterministic model and the probabilistic model introduced by Yang [22]. Moreover, there exists a one-to-one mapping between probabilistic schemes with no expansion and deterministic schemes; such a mapping trades the contrast of the deterministic scheme with the probability factor of the probabilistic scheme. Other proposals in literature have been introduced to deal with non-OR-based vcs and to extend the approach to color and grayscale images.

5.2 Visual Cryptography Schemes

A formal definition of the probabilistic model has been given in [11], generalizing Yang’s approach and extending the traditional definition of VCS. In the next subsection we review the notions related to traditional VCS, before introducing the definition of probabilistic visual cryptography schemes in subsection 5.2.2

5.2.1 The Deterministic Model

The secret image consists of black and white, where usually white color is interpreted as transparent, so that the superposition of white pixels, let the color of the pixel contained in the other shares pass. In order to share each pixel of the secret image the owner of the secret, usually called the dealer, provides each participant with a share, which is an enlarged version of the secret pixel consisting of a certain number m of subpixels. So the shared version of the original secret pixel will consists of m pixels, which are called subpixels because all together they represent the original secret pixel.

The shares can be conveniently represented with n × m matrices where each row represents one share, i.e., m subpixels, and each element is either 0, for a white subpixel, or 1 for a black subpixel. A matrix representing the shares is called the distribution matrix. Physically, the shares are given out in the form of printed transparencies. Given a distribution matrix M and a set Q of participants, the notation M^Q refers to the submatrix of M consisting of only the rows corresponding to participants in Q.

To reconstruct the secret image a group of participants stacks together the shares. Since each secret pixel is represented by m pixels in the shares, the reconstructed image will be bigger than the original (depending on m and on the actual positions of the pixels, the image can also be distorted; a perfect square is a good choice for m because it avoids distortion). Depending on the stacked shares, each secret pixel will be reconstructed with a certain number of black and white subpixels. A reconstructed pixel is considered white if the number of white pixels in its reconstruction is big enough, i.e., the number of black subpixel is less than or equal to a given threshold ℓ, and is considered black if the number of black subpixels is big enough, i.e., greater or equal a given threshold h. Obviously one has to require that ℓ < h. l ℓ and h are called the contrast thresholds of the scheme. In some other papers, the contrast thresholds are used slightly differently: m − h is an upper bound on the number of black subpixels in a white pixel and m − ℓ is a lower bound on the number of black subpixels in a black pixel.

Since a reconstructed pixel has to be either black or white, we consider only schemes such that in the reconstructed image each reconstructed pixel has a number of black pixels, which is either ≤; ℓ or ≥; h. An easy way to resolve ambiguities in the reconstruction is to assume ℓ = h − 1.

We consider threshold schemes where a qualified set of participants consists of k or more participants. For these schemes, a nonqualified set of participants, i.e., a set of less than k participants, will not have any information about the secret image from the shares. Instead, a qualified set of participants, i.e., a set of at least k participants will be able to reconstruct the secret image. The quality of the reconstructed image depends on the scheme.

In a deterministic scheme the quality of the reconstructed image depends on the so-called contrast that is a function of the pixel expansion m, and the contrast thresholds ℓ and h. The contrast of a scheme is defined as γ = (h − ℓ)/m.

In a deterministic scheme it is guaranteed that, for any qualified set of participants, the pixel is reconstructed correctly; that is, if the secret pixel is white then the number of black subpixels in the reconstructed image, corresponding to that secret pixel, is at most ℓ, whereas if the secret pixel is black, the number of black subpixels in the reconstructed pixel is at least h.

In order to provide shares to the participants the dealer chooses uniformly at random a distribution matrix from a collection of matrices CB $C_{B}$ , if the secret pixel is black, or from a collection of matrices CW $C_{W}$ , if the secret pixel is white. Hence, for a deterministic scheme it holds that for any distribution matrix M of the set CB $C_{B}$ , the reconstruction of a pixel obtained by M^Q for any qualified set Q, gives at least h black subpixels, whereas for any distribution matrix M of the set CW $C_{W}$ the reconstruction of a pixel obtained by M^Q for any qualified set Q, gives at most ℓ black subpixels. Let us report here the formal definition of a deterministic VCS:

Definition 1 Let (Г_Qual Г_Qual) be an access structure on a set of n participants. Two collections (multisets) of n × m boolean matrices CW $C_{W}$ and CB $C_{ℬ}$ constitute a visual cryptography scheme (Г_Qual Г_Forb, m)-VCS if there exist the integers ℓ and h, ℓ < h, such that:

Any (qualified) set Q ={i₂,i₂,…, i_p} ∈ Г_Qual can recover the shared image by stacking their transparencies.

Formally, for any M ∈ CW $C_{W}$ , the ”or” V of rows i₁, i₂, …, i_p satisfies w(V) ≤; ℓ; whereas, for any M ∈CB $C_{ℬ}$ it results that w(V) ≥ h.
Any (forbidden) set X = {i₂,i₂,…, i_p} ∈ Г_Forb has no information on the shared image.

Formally, the two collections of p×m matrices Dt $D_{t}$ , with t ∈ {B,W}, obtained by restricting each n × m matrix in CX $C_{X}$ to rows i₂, i₂,…, i_p are indistinguishable in the sense that they contain the same matrices with the same frequencies.

In many schemes, the collection CW $C_{W}$ (resp. CB $C_{B}$ ) consists of all the matrices that can be obtained by permuting all the columns of a matrix M_W (resp. M_B ). For such schemes, the matrices M_W and M_B are called the base matrices of the scheme. Base matrices constitute an efficient representation of the scheme. Indeed, the dealer has to store only the base matrices and in order to randomly choose a matrix from CX $C_{X}$ he has to randomly choose a permutation of the columns of the base matrix M_X.

A scheme is characterized by several parameters: the number of participants n, the threshold k that determines whether a set of participants is qualified to reconstruct the image, the pixel expansion m, and the contrast thresholds ℓ and h, which determine whether a reconstructed pixel is considered white or black.

5.2.2 The Probabilistic Model

In a probabilistic scheme the reconstruction property is no more guaranteed, but each pixel can be correctly reconstructed only with a probability given as a parameter of the schema. This means that the distribution matrices must be carefully selected in order to satisfy the above properties. For a probabilistic scheme, as done in [22], it is possible to define the probabilities of (un)correctly reconstructing a (black)white pixel, given a qualified set of participants Q. With p_i|j is denoted the probability of having a reconstructed pixel i, given that the corresponding pixel in the secret image was j, where i,j ∈ {b,w}. Then p_w|w(Q), denotes the probability of correctly reconstructing a white pixel when superimposing the shares of Q, and p_b|w (Q) as the probability of incorrectly reconstructing a white pixel. Notice that pw∣∣w(Q)=z|CW| $p_{w} |_{w} (Q) = \frac{z}{| C_{W} |}$ where z is the number of distribution matrices M in CW $C_{W}$ for which M^Q reconstructs a pixel with at most ℓ black subpixels and pb∣∣w(Q)=z|CW| $p_{b} |_{w} (Q) = \frac{z}{| C_{W} |}$ where z is the number of distribution matrices M in CW $C_{W}$ for which M^Q reconstructs a pixel with at least h black subpixels. In a similar way p_b|b(Q) and p_w|b(Q) can be defined.

The quantities

p b | b (Q) - p b | w (Q)

$p_{b | b} (Q) - p_{b | w} (Q)$

and

p w | w (Q) - p w | b (Q)

$p_{w | w} (Q) - p_{w | b} (Q)$

return then a measure of the goodness of the scheme for the given qualified set Q. The bigger the above differences the better is the scheme. If both quantities are equal to 1 for all qualified sets, then the scheme is again a deterministic one, with no possible error in the reconstruction.

If there exists a positive constant β such that for any qualified set Q it holds

p b | b (Q) - p b | w (Q) \geq β

$p_{b | b} (Q) - p_{b | w} (Q) \geq β$

and

p w | w (Q) - p w | b (Q) \geq β .

$p_{w | w} (Q) - p_{w | b} (Q) \geq β .$

then the scheme is called β-probabilistic, meaning that β denotes the possible error in the reconstruction. Notice that when every reconstructed pixel is either white or black, that is, the reconstructed pixel has at most ℓ black subpixels or at least h black subpixels, we have that for any Q,

p w | w (Q) = 1 - p b | w (Q)

$p_{w | w} (Q) = 1 - p_{b | w} (Q)$

and that

p b | b (Q) = 1 - p w | b (Q)

$p_{b | b} (Q) = 1 - p_{w | b} (Q)$

and thus,

p w | w (Q) - p w | b (Q) = p b | b (Q) - p b | w (Q) .

$p_{w | w} (Q) - p_{w | b} (Q) = p_{b | b} (Q) - p_{b | w} (Q) .$

The value ℓ and h are the thresholds that define the number of subpixels needed to correctly distinguish between a white and black pixel in the reconstructed image. For some scheme, for some qualified set Q, it could be possible to obtain a secret pixel with a number of black subpixels strictly greater than ℓ and strictly less than h, where the reconstructed pixel is neither white nor black. In this case the value p_b|b(Q) − p_b|w(Q) might be different from p_w|w(Q) − p_w|b(Q). To avoid such kind of ambiguous situations, it is possible to fix the value ℓ = h − 1, so that the equation p_w|w(Q) − p_w|b(Q). = p_b|b(Q) − p_b|w(Q) always holds.

Probabilistic schemes are then characterized by a further parameter: the probabilistic factor β. In the following a probabilistic scheme will be described by all these parameters (that is, β, k, n, ℓ, h, and m) which are referred to as the characteristic parameters of the scheme.

It is now possible to provide the formal definition of a β-probabilistic threshold visual cryptography scheme with characteristic parameters (k, n, ℓ, h, m), for short β-probabilistic (k, n, ℓ, h, m)-VCS. The definition naturally extends also to general access structures.

Definition 2 A β-probabilistic (k, n, ℓ, h, m)-VCS consists of two collections of n × m binary matrices, CW $C_{W}$ and CB $C_{B}$ , satisfying the following properties:

There exists β > 0, such that for any set Q of exact k participants p_b|b(Q) − p_b|w (Q) ≥ β and p_w|w (Q) − p_w|b(Q) ≥ β
For any set Q of strictly less than k participants, the sets CQW={MQ∣∣M∈CW} $C_{W}^{Q} = {M^{Q} | M \in C_{W}}$ and CQW={MQ∣∣M∈CB} $C_{W}^{Q} = {M^{Q} | M \in C_{B}}$ are equal.

Notice that the definition of the scheme requires the reconstruction of a secret pixel (Property 1) to be well defined for qualified sets of exact k participants. This is without loss of generality because if a qualified set has more than k participants one can simply choose k of the shares and use only those k shares to reconstruct the image. Hence in the rest of the chapter a qualified set is assumed to consist of exact k participants.

The goodness of a scheme is measured by the pixel expansion m, the contrast γ = (h − ℓ) /m and by the probabilistic factor β. Notice that for m =1 the above definition is equivalent to the one provided by Yang [22]. Whereas for a big enough m, it is possible to construct schemes with β = 1, and in such a case the above definition is equivalent to the classical definition of a visual cryptography scheme.

If the pixel expansion m is assumed to be a parameter of a scheme, then on one extreme, when m = 1 one gets the probabilistic model with no pixel expansion, and on the other extreme, when m is big enough, one obtains the deterministic model. In between such two extremes it is possible to consider probabilistic models with a given pixel expansion, trading the probability of a good reconstruction with the number of subpixels required to reconstruct each secret pixel.

5.3 Canonical Probabilistic Schemes

By restricting the attention on a particular class of probabilistic schemes, it is possible to show that results valid for all the other schemes can be obtained, without loss of generality. The trick is to prove that for a given scheme it is possible to define a similar scheme satisfying well-defined additional properties, without modification on the parameters of the scheme. For this reason canonical β-probabilistic (k, n, ℓ, h, m)-VCS schemes are defined as those schemes that satisfy the following properties:

The cardinality of the collections CW $C_{W}$ and CB $C_{B}$ are equal and
For any two qualified sets Q₁ and Q₂ of participants, we have that p_x|y(Q₁) = p_x|y(Q₂), for x ∈ {w, b} and y ∈ {w, b}.

The first lemma says that given a probabilistic scheme S a new scheme S' can be constructed such that the cardinality of CW(S′) $C_{W} (S^{'})$ is the same as that of CB(S′) $C_{B} (S^{'})$ and such that S' has the same characteristic parameters as S.

The following lemma is similar to the analogous result proved in Section 2.1 of [1] for deterministic schemes.

Lemma 1 Given a β-probabilistic (k,n, ℓ,h,m)-VCS S, there exists a β-probabilistic (k, n, ℓ, h, m)-VCS S' such that |CW(S′)|=|CB(S′)| $| C_{W} (S^{'}) | = | C_{B} (S^{'}) |$ .

Proof Fix a β-probabilistic (k,n, ℓ,h,m)-VCS S, let r1=|CW(S)| and r2=CB(S) $r_{1} = | C_{W} (S) | a n d r_{2} = C_{B} (S)$ and assume that r₁ ≠ r₂ (otherwise we can choose S' = S and we are done). Let r = r₁ r₂ and construct S' by letting CW(S′) (resp. CB(S′) $C_{W} (S^{'}) (r e s p . C_{B} (S^{'})$ ) consists of all the matrices of CW(S) (resp. CB(S) $C_{W} (S) (r e s p . C_{B} (S)$ ) each one repeated r₂ (resp. r₁) times. It is obvious that |CW(S′)|=|CB(S′)|=r $| C_{W} (S^{'}) | = | C_{B} (S^{'}) | = r$

Since we have only repeated matrices of the collections C $C$ it is easy to see that k, n, and m remain the same. Keeping the same ℓ and h also β stays the same: indeed CW(S′) $C_{W} (S^{'})$ is obtained by replicating the same number of times each matrix of CW(S) $C_{W} (S)$ and thus the probabilities p_w|w (Q) and p_b|w (Q) do not change for any Q and similarly for p_w|b(Q) and p_b|b(Q) since CB(S′) $C_{B} (S^{'})$ is obtained by replicating the same number of times each matrix of CB(S) $C_{B} (S)$ .

The following lemma shows that schemes can be built where the number of black subpixels in a reconstructed pixel does not depend on the particular qualified set of participants chosen to reconstruct the secret pixel and the characteristic parameters remain the same.

Lemma 2 Given a β-probabilistic (k, n, ℓ, h, m)-VCS S, there exists a β-probabilistic (k,n,ℓ, h, m)-VCS S' such that for any two qualified sets Q₁ and Q₂ of participants, we have that p_x|y(Q₁) = p_x|y(Q₂), for x ∈ {w, b} and ^y ∈ ^{w,b}.

Proof Fixa β-probabilistic (k,n, ℓ,h,m)-VCS S. Consider first CW(S) $C_{W} (S)$ and assume that the desired property does not hold. Then we build a new scheme S' where CW(S′) $C_{W} (S^{'})$ is obtained from CW(S) $C_{W} (S)$ in the following way: for each matrix M of CW(S) $C_{W} (S)$ insert into CW(S′) $C_{W} (S^{'})$ all the matrices that we can build from M by permuting in all possible n! ways its rows. The collection CB(S′) $C_{B} (S^{'})$ is obtained in the same way from CB(S) $C_{B} (S)$ .

Let Q₁ and Q₂ be two qualified sets. We have that CQ1W(S′)=CQ2W(S′) $C_{W}^{Q_{1}} (S^{'}) = C_{W}^{Q_{2}} (S^{'})$ ; indeed, by construction both sets contain, for any qualified set Q, all the matrices in CQW(S) $C_{W}^{Q} (S)$ , with the same multiplicity (the multiplicity is due to the fact that when restricting the attention to the rows in Q, the other n − k rows can be taken in any order). Hence, we have that p_w|w(Q₁) = p_w|w(Q₂), and p_b|w(Q₁) = p_b|w(Q₂). For the same reason we have CQ1B(S′)=CQ2B(S′) $C_{B}^{Q_{1}} (S^{'}) = C_{B}^{Q_{2}} (S^{'})$ and thus p_b|b(Q₁) = p_b|b(Q₂), and p_w|b(Q₁) = p_w|b(Q₂).

By Lemmas 1 and 2, it follows that considering only canonical schemes is without loss of generality, because for any scheme S an equivalent canonical scheme S' having the same characteristic parameters of scheme S can be provided.

In the following only canonical schemes will be considered, remembering that for a canonical scheme p_x|y(Q₁) = p_x|y(Q₂), for x ∈ {w, b} and y ∈ {w, b} and thus we will just write p_x|y, without specifying the qualified set.

5.4 Probabilistic Schemes with No Pixel Expansion

Probabilistic threshold schemes give the possibility to construct a VCS scheme with no pixel expansion, that is having m = 1. In [22] it has been proved that a deterministic scheme S with contrast γ(S) can be transformed into a β-probabilistic scheme S' with β(S') = γ(S) and no pixel expansion. In [11] a complementary result has been proven showing that there is a one-to-one correspondence between the probabilistic model with no pixel expansion and the deterministic one where the contrast is traded for the probabilistic factor. Indeed a β-probabilistic scheme S with no pixel expansion can be transformed into a deterministic scheme S' with contrast γ(S') = β(S). An immediate consequence is that any bound on the contrast of a deterministic scheme is also a bound on the probabilistic factor of probabilistic schemes with no pixel expansion. In the following we report the lemma proving the correspondence between probabilistic schemes with no pixel expansion and deterministic schemes.

The following lemma has been proved in [22] and applies to VCS with basis matrices.

Lemma 3 [22] Let S be a deterministic (k, n, ℓ, h, m)-VCS with base matrices M_B and M_W. Then, there exists a canonical β-probabilistic (k, n, ℓ', h', 1)-VCS scheme with β = γ(S).

Proof Let S be a deterministic (k, n, ℓ, h, m)-VCS. Construct a probabilistic scheme S', by letting CB(S′) (resp. CW(S′) $C_{B} (S^{'}) (r e s p . C_{W} (S^{'})$ ) consists of all the n × 1 vectors that appear in the matrices M_B (resp. M_W).

We need to prove that S' is a β-probabilistic (k, n, ℓ', h', m')-VCS scheme with ℓ' = ℓ, h' = h, m' = 1 and β = γ(S) = (h − ℓ)/m. Obviously S' has pixel expansion m' = 1.

By the properties of S, we know that when the secret pixel is black the reconstruction in S gives at least h black subpixels, that is p_b|b ≥h/m. Obviously this gives p_w|b ≥ (m − h)/m. Similarly, we have p_w|w ≥ (m − ℓ)/m and p_b|w≤ ℓ/m.

Hence, in S' we have that

p w | w - p w | b \geq m - ℓ m - m - h m = h - ℓ m

$p_{w | w} - p_{w | b} \geq \frac{m - ℓ}{m} - \frac{m - h}{m} = \frac{h - ℓ}{m}$

and

p b | b - p b | w \geq h m - ℓ m = h - ℓ m

$p_{b | b} - p_{b | w} \geq \frac{h}{m} - \frac{ℓ}{m} = \frac{h - ℓ}{m}$

and thus we can set β=h−ℓm $β = \frac{h - ℓ}{m}$ The security property is immediate.

Example 1 Consider as starting point the deterministic scheme (3, 4) having basis matrices M_W and M_B reported below, whose parameters are m = 6, h = 5, ℓ = 4, a = 1/6:

M W = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 000000001110110110110111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ M B = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 111111110001001001001000 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ .

$\begin{matrix} M_{W} = [\begin{matrix} 0 & 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{matrix}] & M_{B} = \end{matrix} [\begin{matrix} 1 & 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \end{matrix}] .$

To illustrate the construction, consider the following 16 $\frac{1}{6}$ -probabilistic (3,4,4, 5,1)-VCS S.

c W = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0000 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0000 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1110 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1101 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1011 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ c B = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0001 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0010 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0100 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1000 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ .

$\begin{matrix} c_{W} = {[\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 1 \\ 1 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 1 \\ 0 \\ 1 \end{matrix}], [\begin{matrix} 1 \\ 0 \\ 1 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 1 \\ 1 \\ 1 \end{matrix}]} \\ c_{B} = {[\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix}], [\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 1 \\ 0 \end{matrix}], [\begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix}]} . \end{matrix}$

Let S be the (n,n, 0, 0, 1)-VCS obtained applying Lemma 3 to scheme S_D. For scheme S we have that p_b|b = 5/6, p_w|b = 1/6, p_w|w = 1/3, p_b|w = 2/3,β = γ(S) = 1/6.

Lemma 3 shows how starting from a deterministic scheme with base matrices it is possible to obtain a corresponding probabilistic scheme. A more general version of the above lemma we report below has been given in [11] showing the transformation from a general (also with no base matrices) deterministic scheme to a probabilistic one.

Lemma 4 Let S be a deterministic (k,n, ℓ, h,m)-VCS. Then, there exists a canonical β-probabilistic (k, n, 0, 1, 1)-VCS scheme with β = γ(S).

Proof Let S be a deterministic (k,n, ℓ, h,m)-VCS. Construct a probabilistic scheme S', by letting CB $C_{B}$ (S′) (resp. CW(S′) $C_{W} (S^{'})$ ) consists of all the n × 1 vectors that appear in all the matrices ofCB(S′) (resp. CW(S)) $C_{B} (S^{'}) (r e s p . C_{W} (S))$ ).

We need to prove that S′ is a β-probabilistic (k, n, ℓ′, h′, m′)-VCS scheme with ℓ′ = 0, h′ = 1 , m^''= 1 and β = γ(S) = (h − ℓ)/m. Obviously S' has pixel expansion m' = 1. We set ℓ' = 0 and h' = 1 and we have to prove that this results in a β-probabilistic scheme.

Let r=|CB(S)| $r = | C_{B} (S) |$ . By the properties of S, we know that when the secret pixel is black the reconstruction in S gives at least h black subpixels, that each matrix of CB(S) $C_{B} (S)$ has at least h columns, which reconstruct black. Hence, in S' we have at least r • h columns that reconstruct black. Since |CB(S′)| $| C_{B} (S^{'}) |$ = r • m we have that p_{b| b} ≥ h/m. Obviously this gives p_{w| b} ≤ (m − h)/m. Similarly, we have p_{w| w} ≥ (m − ℓ)/m and p_{b| w} ≤ ℓ/m.

Hence, in S′ we have that pw|w−pw|b≥h−ℓm $p_{w | w} - p_{w | b} \geq \frac{h - ℓ}{m}$ and pb|b−pb|w≥h−ℓm $p_{b | b} - p_{b | w} \geq \frac{h - ℓ}{m}$ and thus we can set β=h−ℓm $β = \frac{h - ℓ}{m}$ . The security property is immediate.

For a canonical scheme it is possible to define the characteristic vectors as:

c B = (c 0 B, c 1 B, \dots, c m B)

$c_{B} = (c_{B}^{0}, c_{B}^{1}, \dots, c_{B}^{m})$

and

c W = (c 0 W, c 1 W, \dots, c m W)

$c_{W} = (c_{W}^{0}, c_{W}^{1}, \dots, c_{W}^{m})$

where CiX $C_{X}^{i}$ is the number of matrices of CX $C_{X}$ that provide a reconstruction, by any qualified set, of the secret pixel with exactly i black subpixels. The characteristic vectors are well defined because, by Property 2 of canonical schemes, each CiX $C_{X}^{i}$ does not depend on the particular qualified set chosen for reconstructing the secret pixel.

The following lemma complements the results presented above, showing how it is possible to transform a probabilistic (canonical) scheme into a deterministic scheme.

Lemma 5 Let S be a β-probabilistic canonical (k, n, 0,1,1)-VCS and let C_B = (C0B,C1B $C_{B}^{0}, C_{B}^{1}$ ) and c_W = (C0W,C1W $C_{W}^{0}, C_{W}^{1}$ ) be its characteristic vectors. Then, there exists a deterministic (k, n, ℓ′, h′, m′)-VCS S′ with ℓ′ = c1W, h′=c1B, m′=|CW(S)| $c_{W}^{1}, h^{'} = c_{B}^{1}, m^{'} = | C_{W} (S) |$ and contrast γ(S′) ≥ β(S).

Proof Let S be a β-probabilistic (k, n, 0, 1, 1)-VCS satisfying the hypothesis of the lemma. Scheme S' is constructed by letting its base matrix M_B (resp. M_w) consist of all the vectors of CB(S) $C_{B} (S)$ (resp. CW(S) $C_{W} (S)$ ). Fix ℓ′ = c1W $c_{W}^{1}$ and h′=c1B $h^{'} = c_{B}^{1}$ We have to prove that S' is a deterministic (k, n, ℓ′, h′, m′)-VCS with m' = r, where r=|CW(S)|=|CB(S)| $r = | C_{W} (S) | = | C_{B} (S) |$

Both CB (S) and CW (S) contain r matrices of dimension n x 1; hence, the dimension of both M_B and M_W is n × r; thus, m' = r.

Since S is a β-probabilistic scheme, we have that− p_b|b ≥ β > 0 hence, p_b|b > p_b|w, and since = pb|b=c1B/r $p_{b | b} = c_{B}^{1} / r$ and = pb|w=c1W/r $p_{b | w} = c_{W}^{1} / r$ , we have c1B>c1W $c_{B}^{1} > c_{W}^{1}$ . Thus, ℓ′ < h′. Now we need prove that the scheme is deterministic. Scheme S′ is a basis matrices scheme, so all the matrices of the collections CW(S′) $C_{W} (S^{'})$ and CB(S′′) $C_{B} (S^{″})$ are equal up to a permutation of the columns; moreover it is easy to see that a reconstructed black pixel always has h' black subpixels and that a reconstructed white pixel always has ℓ' black subpixels. Hence, we have p′b|b=p′w|w=1 ${p^{'}}_{b | b} = {p^{'}}_{w | w} = 1$ and p′w|b=p′b|w=0 ${p^{'}}_{w | b} = {p^{'}}_{b | w} = 0$ Hence, scheme S' is deterministic.

Let us consider the security property. Fix a nonqualified set of participants and consider the corresponding k' < k rows of the basis matrices. Each of these rows can be seen as the concatenation of shares of S (one per each matrix in the collections CB(S) $C_{B} (S)$ and CW(S) $C_{W} (S)$ ). By the security property of S we have that the k′ rows of M_B are equal to the k' rows of M_W, except for a permutation of the columns. Hence, S' satisfies the security property.

Finally, the contrast of S' is γ(S′)=h′−ℓ′m′=c1B−c1Wr=pb|b−pb|w≥β(S) $γ (S^{'}) = \frac{h^{'} - ℓ^{'}}{m^{'}} = \frac{c_{B}^{1} - c_{W}^{1}}{r} = p_{b | b} - p_{b | w} \geq β (S)$ .

As already said, the correspondence between deterministic schemes and probabilistic schemes with no pixel expansion allows the reuse of bounds found on the contrast as bounds on the corresponding probabilistic factor. For example, in [14] it has been proved that the contrast of any deterministic (2, n)-VCS is upper bounded by

γ \leq γ * = 4 - (k - 1) n k n ( n - 1 ) \dots ( n - ( k - 1 ) ) . (5.1)

$γ \leq γ^{*} = 4^{- (k - 1)} \frac{n^{k}}{n (n - 1) \dots (n - (k - 1))} . (5.1)$

As an immediate, the following lemma, which is a corollary of Lemma 5, also holds:

Corollary 6 For any β-probabilistic (2,n, 0, 1,1)-VCS we have that

β \leq β * = 4 - (k - 1) n k n ( n - 1 ) \dots ( n - ( k - 1 ) ) .

$β \leq β^{*} = 4^{- (k - 1)} \frac{n^{k}}{n (n - 1) \dots (n - (k - 1))} .$

Proof Assume by contradiction that a probabilistic scheme with β > β* exists. By Lemma 5, we can construct a scheme with contrast γ ≥ β. Since β > β* = γ* we get that γ > γ*, contradicting Equation (5.1).

5.5 Trading Pixel Expansion with Probabilities

In the above section, the correspondence between deterministic and probabilistic schemes has been stated in Lemma 3 and Lemma 5, showing a trade-off between pixel expansion and probability factor. It shows that by using a large enough pixel expansion we can transform a probabilistic scheme into a deterministic one. Indeed, on one extreme it is possible to have schemes with no pixel expansion, where the reconstruction relies entirely on the probability factor of the scheme. On the other extreme, it is possible to have deterministic schemes, where the reconstruction is guaranteed but a certain pixel expansion is required. In the next section we show how it is possible to stay in between the two extremes, realizing schemes for which the probability factor is traded for the pixel expansion.

5.5.1 Probabilistic Schemes with Given Pixel Expansion

Lemma 5 shows the basic technique for the construction of a deterministic scheme with pixel expansion equal to the cardinality r of the collections CB $C_{B}$ and CW $C_{W}$ of the probabilistic scheme with no pixel expansion taken as a starting point. Extending such a technique, it is possible to obtain schemes with arbitrary pixel expansion m', with 1 < m' ≤ r. The new collections of matrices C′B ${C^{'}}_{B}$ and C′W ${C^{'}}_{W}$ for the resulting scheme is built by constructing in all possible ways matrices with m' columns from the vectors of the collections CB $C_{B}$ and CW $C_{W}$ of the starting probabilistic scheme (in the particular case of m' = r, the resulting scheme is deterministic). We remark that Construction 1 does not allow repetition of the same column. It is possible to build schemes by also allowing repetitions of the columns; however, the resulting schemes have a worst probabilistic factor. Notice that it is useless to construct probabilistic schemes with m' > r, since if m' = r then a deterministic scheme can be realized.

Construction 1 Let S be a canonical β-probabilistic (k,n, 0, 1, 1)-VCS. Fix 1 < m' ≤ r, where r=|CB(S)|=|CW(S)| $r = | C_{B} (S) | = | C_{W} (S) |$ Construct a scheme S' whose collection CB(S′) $C_{B} (S^{'})$ (resp. CW(S′) $C_{W} (S^{'})$ ) consists of all the matrices of dimension n × m' that we can build by choosing m' vectors of CB(S) $C_{B} (S)$ (resp. CW(S) $C_{W} (S)$ ).

Notice that we also need to fix the contrast thresholds ℓ' and h' of the new scheme S'. There can be several valid choices.

To illustrate the construction, consider the following 1/3-probabilistic (2, 3,0,1,1)-VCS S.

c B = ⎧ ⎩ ⎨ ⎪ ⎪ ⎡ ⎣ ⎢ 100 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 010 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 001 ⎤ ⎦ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ c W = ⎧ ⎩ ⎨ ⎪ ⎪ ⎡ ⎣ ⎢ 111 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 000 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 000 ⎤ ⎦ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ .

$\begin{matrix} c_{B} = {[\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 0 \\ 1 \\ 0 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}]} & c_{W} = {[\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 0 \end{matrix}]} . \end{matrix}$

For such a scheme, the parameters are p_b|b = 2/3 and p_b|w = 1/3.

If m' = 2 is fixed, a 3-probabilistic (2, 3, •, •, 2)-VCS is obtained by applying Construction 1 to scheme S:

c B = ⎧ ⎩ ⎨ ⎪ ⎪ ⎡ ⎣ ⎢ 100010 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 100001 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 010001 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 010100 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 001100 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 001010 ⎤ ⎦ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ c W = ⎧ ⎩ ⎨ ⎪ ⎪ ⎡ ⎣ ⎢ 111000 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 111000 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 000000 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 000111 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 000111 ⎤ ⎦ ⎥, ⎡ ⎣ ⎢ 000000 ⎤ ⎦ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ .

$\begin{matrix} c_{B} = {[\begin{matrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{matrix}], [\begin{matrix} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{matrix}], [\begin{matrix} 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{matrix}], [\begin{matrix} 0 & 1 \\ 1 & 0 \\ 0 & 0 \end{matrix}], [\begin{matrix} 0 & 1 \\ 0 & 0 \\ 1 & 0 \end{matrix}], [\begin{matrix} 0 & 0 \\ 0 & 1 \\ 1 & 0 \end{matrix}]} \\ c_{W} = {[\begin{matrix} 1 & 0 \\ 1 & 0 \\ 1 & 0 \end{matrix}], [\begin{matrix} 1 & 0 \\ 1 & 0 \\ 1 & 0 \end{matrix}], [\begin{matrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{matrix}], [\begin{matrix} 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{matrix}], [\begin{matrix} 0 & 1 \\ 0 & 1 \\ 0 & 1 \end{matrix}], [\begin{matrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{matrix}]} . \end{matrix}$

The thresholds of S' can be selected in different ways returning in every case a 13 $\frac{1}{3}$ -probabilistic scheme. If values ℓ' = 0 and h' =1 are selected, the resulting probabilities for the scheme S' are p′b|b=1 ${p^{'}}_{b | b} = 1$ and p_b|w = 2/3. For ℓ' = 1 and h' = 2, scheme S' has p′b|b=1/3 ${p^{'}}_{b | b} = 1 / 3$ and p′b|w=0 ${p^{'}}_{b | w} = 0$ . As already said, here we are considering values satisfying the condition ℓ' = h' − 1. Notice that for the values the case ℓ' = 0 and h' = 2, some reconstructed pixels cannot be classified as either black or white. In such a scheme the probabilities of correctly reconstructing secret pixels are smaller (since some of the matrices are wasted with a reconstruction that is neither black nor white). We also remark that one could try to eliminate distribution matrices for which the reconstruction gives a number of black subpixels in the gap between ℓ' and h'; however it is not clear whether this can be done without violating the security property. In the particular case above, ℓ' = 0 and h' = 2 is clearly not possible (indeed we would have a perfect reconstruction of both white and black). One could also extend the formal model to allow this possibility; but then the contrast should be redefined in order to account for unclassified reconstructed pixels.

The matrices M_B and M_w consisting of all the columns of CB $C_{B}$ and CW $C_{W}$ can be used to represent the new scheme S', since they give an efficient representation of the collections C′B ${C^{'}}_{B}$ and C′W ${C^{'}}_{W}$ ; clearly together with M_B and M_w, the pixel expansion m' and the thresholds ℓ' and h' need to be specified.

Construction 1 starts from probabilistic schemes with no pixel expansion. Using Lemma 3 or Lemma 4 a probabilistic scheme with no pixel expansion can be obtained starting from a deterministic scheme. Hence, probabilistic schemes with pixel expansion can be constructed by starting from a deterministic scheme, applying first Lemma 3 and then Construction 1.

The probabilistic schemes obtained with Construction 1 satisfy the security property. Indeed, consider a nonqualified set Q of participants and let CQW(S) $C_{W}^{Q} (S)$ (resp. CQB(S) $C_{B}^{Q} (S)$ ) be the vectors of CW(S) $C_{W} (S)$ (resp. CB(S) $C_{B} (S)$ ) restricted to the rows corresponding to participants in Q. By the security property of S, CQW(S) $C_{W}^{Q} (S)$ and CQB(S) $C_{B}^{Q} (S)$ are the same collection of vectors. Since the way in which CW(S′) $C_{W} (S^{'})$ and CB(S′) $C_{B} (S^{'})$ are constructed is the same (except that for the former we start from CW(S′) $C_{W} (S^{'})$ and for the latter from CB(S) $C_{B} (S)$ ), also CQW(S′) $C_{W}^{Q} (S^{'})$ and CQB(S′) $C_{B}^{Q} (S^{'})$ are the same collection of matrices. Hence, the security property for S' holds.

In this section, a formula for the probabilities of the scheme built with Construction 1 as a function of the probabilities of the starting scheme is provided. Let S be a canonical probabilistic scheme with no pixel expansion and let p_b|b, p_b|w, p_w|b and p_w|w be the probabilities of S.

Fix an m' and build a probabilistic scheme with pixel expansion m' using Construction 1. Fix also a threshold ℓ', 0 ≤ ℓ' < m'. Fixing ℓ' also gives h' = ℓ' + 1. Notice that, even with this restriction, not all choices of ℓ' will result in valid schemes. Let r be the cardinality of the collections CW $C_{W}$ and CB $C_{B}$ of S.

The cardinality of the collections C′W ${C^{'}}_{W}$ and C′B ${C^{'}}_{B}$ , of scheme S', is r' = r(r − 1) • … • (r − m' + 1) because the first column can be selected in r ways, the second in r − 1 ways, and so on until the last column for which r − m' + 1 choices are possible. It is easy to see that r′=m′!(rm′) $r^{'} = m^{'}! (\begin{matrix} r \\ m^{'} \end{matrix})$ . An explanation of this expression is that the binomial coefficient gives the number of possible ways of choosing m' vectors among the r of the collections, and the factorial coefficient accounts for all the possible permutations for each choice.

Fix a qualified set Q of participants. To compute p′b|b(Q) ${p^{'}}_{b | b} (Q)$ , the number of matrices of CQB(S) $C_{B}^{Q} (S)$ that yield a black reconstructed pixel is needed. Notice that, for a qualified set, the number of matrices (vectors) CQB(S) $C_{B}^{Q} (S)$ that would give the correct reconstruction of a black subpixel (i.e., a black pixel) is r • p_{b| b}, while the remaining r − r • p_b|b, would give a wrong reconstruction of a black secret pixel (i.e., a white pixel). Recall that since S is canonical, p_b|b does not depend on Q. Hence, the number of matrices in CB(S′) $C_{B} (S^{'})$ that will have a certain number z of black subpixels, is given by

m'! (r \cdot p b | b z) (r - r \cdot p b | b m' - z)

$m^{'}! (\begin{matrix} r \cdot p_{b | b} \\ z \end{matrix}) (\begin{matrix} r - r \cdot p_{b | b} \\ m^{'} - z \end{matrix})$

because z vectors can be selected from the r • p_b|b vectors that yield a reconstructed black subpixel, and m' − z vectors from the r − r • p_{b| b} ones that yield a reconstructed white subpixel. Hence, z is constrained by 0 ≤ z < r • p_{b| b} and 0 ≤ m' − z ≤ r − r • p_b|b, which implies that binomial coefficients are defined. (By definition (00)=1 $(\begin{matrix} 0 \\ 0 \end{matrix}) = 1$ and that (ab)=0 $(\begin{matrix} a \\ b \end{matrix}) = 0$ when b > a.) Hence, the values for the probabilities of the resulting scheme can be expressed as follows:

p' b | b (Q) = \sum m ' z = h ' ( r \cdot p b | b z ) ( r - r \cdot p b | b m ' - z ) ( r m ' ) (5.2)

${p^{'}}_{b | b} (Q) = \frac{\sum_{z = h^{'}}^{m^{'}} (\begin{matrix} r \cdot p_{b | b} \\ z \end{matrix}) (\begin{matrix} r - r \cdot p_{b | b} \\ m^{'} - z \end{matrix})}{(\begin{matrix} r \\ m^{'} \end{matrix})} (5.2)$

and similarly

p' b | w (Q) = \sum m ' z = h ' ( r \cdot p b | w z ) ( r - r \cdot p b | w m ' - z ) ( r m ' ) (5.3)

${p^{'}}_{b | w} (Q) = \frac{\sum_{z = h^{'}}^{m^{'}} (\begin{matrix} r \cdot p_{b | w} \\ z \end{matrix}) (\begin{matrix} r - r \cdot p_{b | w} \\ m^{'} - z \end{matrix})}{(\begin{matrix} r \\ m^{'} \end{matrix})} (5.3)$

p' w | w (Q) = \sum ℓ ' z = 0 ( r - r \cdot p w | w z ) ( r \cdot p w | w m ' - z ) ( r m ' ) (5.4)

${p^{'}}_{w | w} (Q) = \frac{\sum_{z = 0}^{ℓ^{'}} (\begin{matrix} r - r \cdot p_{w | w} \\ z \end{matrix}) (\begin{matrix} r \cdot p_{w | w} \\ m^{'} - z \end{matrix})}{(\begin{matrix} r \\ m^{'} \end{matrix})} (5.4)$

p' w | b (Q) = \sum ℓ ' z = 0 ( r - r \cdot p w | b z ) ( r \cdot p w | b m ' - z ) ( r m ' ) . (5.5)

${p^{'}}_{w | b} (Q) = \frac{\sum_{z = 0}^{ℓ^{'}} (\begin{matrix} r - r \cdot p_{w | b} \\ z \end{matrix}) (\begin{matrix} r \cdot p_{w | b} \\ m^{'} - z \end{matrix})}{(\begin{matrix} r \\ m^{'} \end{matrix})} . (5.5)$

Since from Equations 5.2–5.5, probabilities of S' do not depend on the particular qualified set Q, it is possible to conclude that S' is canonical.

5.6 Constructing Probabilistic Schemes

The construction previously described can be applied for the construction of novel probabilistic schemes. The starting point however is the selection of a particular deterministic scheme that determines the parameters of the resulting scheme. Obviously, by changing the selected scheme, diferent probabilistic schemes are obtained. In the next sections we will describe some probabilistic schemes for the (n, n) and the (2, n) cases starting from two selected deterministic schemes. In the first case a simple formula for the probabilistic factor can be obtained, relating β to the pixel expansion of the resulting scheme, while in the second case, the computation of the parameters results is more complicated and depends on the selected pixel expansion of the new scheme.

5.6.1 (n, n)-Threshold Probabilistic Schemes with Any Pixel Expansion

In this section a (n, n)-threshold probabilistic schemes with any pixel expansion is built, for n ≥ 2 starting from deterministic scheme S_D, which is the (n, n)-threshold deterministic scheme of Naor and Shamir [16]. S_D has pixel expansion m = 2ⁿ⁻¹, and thresholds ℓ = m − 1 and h = m. Moreover, the scheme consists of a white base matrix containing all vectors with an even (including 0) number of black subpixels and a black base matrix containing all vectors with an odd number of black subpixels. For example, for n = 4 the scheme S_D is given by:

M W = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 00001100101010010110010100111111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ M B = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 00010010010010001110110110110111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ .

$\begin{matrix} M_{W} = [\begin{matrix} 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 & 1 \end{matrix}] & M_{B} = [\begin{matrix} 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \end{matrix}] . \end{matrix}$

Let S be the (n, n, 0,0,1)-VCS obtained applying Lemma 3 to scheme S_D. For scheme S we have that the cardinality of the collections C_B and C_W is r = 2ⁿ⁻¹, and that p_b|b = 1, p_w|b = 0, p_w|w = 1/2ⁿ⁻¹, p_b|w = 1 − 1/2ⁿ⁻¹.

c B = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0000 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1100 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1010 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1001 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0110 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0101 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0011 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪

$c_{B} = {[\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 1 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 0 \\ 1 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 0 \\ 0 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 1 \\ 1 \\ 0 \end{matrix}], [\begin{matrix} 0 \\ 1 \\ 0 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 1 \\ 1 \end{matrix}], [\begin{matrix} 1 \\ 1 \\ 1 \\ 1 \end{matrix}]}$

c W = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0001 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0010 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0100 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1000 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1110 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1101 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 1011 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥, ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 0111 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎫ ⎭ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ .

$c_{W} = {[\begin{matrix} 0 \\ 0 \\ 0 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 0 \\ 1 \\ 0 \end{matrix}], [\begin{matrix} 0 \\ 1 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 0 \\ 0 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 1 \\ 1 \\ 0 \end{matrix}], [\begin{matrix} 1 \\ 1 \\ 0 \\ 1 \end{matrix}], [\begin{matrix} 1 \\ 0 \\ 1 \\ 1 \end{matrix}], [\begin{matrix} 0 \\ 1 \\ 1 \\ 1 \end{matrix}]} .$

Fix an m′, 2 ≤ m′ ≤ r, and let S′ be the probabilistic scheme with pixel expansion m′ obtained using Construction 1 from scheme S. The threshold ℓ′ for S′ also needs to be selected, remembering also that the threshold ℓ′ will be obtained if the assumption h′ = ℓ′ + 1 is satisfied. Observe that ℓ′ must be m′ − 1 because there is only one column with all white pixels and thus it would be never possible to get more than 1 white subpixel in a reconstructed pixel (equivalently always at least m′ − 1 black subpixels in a reconstructed pixel will be obtained). This implies that if by selecting ℓ′ < m′ − 1 all reconstructed pixels will always be considered black and thus no valid scheme can be obtained. To construct schemes, values ℓ′ = m′ − 1 and h′ = m′ must be selected.

To compute the probabilistic factor of scheme S′ it is necessary to compute p′b|b ${p^{'}}_{b | b}$ and p′b|w ${p^{'}}_{b | w}$ . All the columns of the black base matrix M_B of the deterministic scheme S_D have at least a 1; hence, all columns of C_B (S′) have at least a 1. Thus, m′ black subpixels when reconstructing a black secret pixel are always returned. This means that p′b|b=1 ${p^{'}}_{b | b} = 1$ and p′w|b=0 ${p^{'}}_{w | b} = 0$ . To compute p′b|w ${p^{'}}_{b | w}$ consider the white base matrix M_W of scheme S_D, which determines C_W (S′). Since M_W has one column with all 0s there will be some matrices of C_W (S′) that include such a column. In order for a reconstructed pixel to be considered black it must have h′ = m′ black subpixels. Among the (rm′) $(\begin{matrix} r \\ m^{'} \end{matrix})$ possible distribution matrices of C_W (S′), exactly (r−1m′) $(\begin{matrix} r - 1 \\ m^{'} \end{matrix})$ do not include the unique column with all 0s. Hence,

p' b | w = (r - 1 m') / (r m') = 1 - m' / r

${p^{'}}_{b | w} = (\begin{matrix} r - 1 \\ m^{'} \end{matrix}) / (\begin{matrix} r \\ m^{'} \end{matrix}) = 1 - m^{'} / r$

and

p' w | w = m' / r

${p^{'}}_{w | w} = m^{'} / r$

The formula expressing the probability factor of S′ is then the following:

β = m ' 2 n - 1 .

$β = \frac{m^{'}}{2^{n - 1}} .$

The formula shows that there is a linear relation between the pixel expansion of the scheme and the probability factor. A probabilistic scheme with no pixel expansion implies a small probability factor ( β = 1/r) and then a reconstructed image with many errors; the probability factor of the scheme can be increased by increasing the pixel expansion to obtain a better reconstructed image. Clearly for m′ = 2ⁿ⁻¹ one would get β =1, that is, a deterministic scheme.

5.6.2 (2, n)-Threshold Probabilistic Schemes with Any Pixel Expansion

In this section a (2, n)-threshold probabilistic scheme with pixel expansion, for n ≥ 3 is provided, starting from the (2, n)-threshold deterministic scheme S_D described in [7]. Recall that S_D has pixel expansion m=(n⌊n2⌋) $m = (\begin{matrix} n \\ ⌊ \frac{n}{2} ⌋ \end{matrix})$ , and thresholds l=(n−1⌊n2⌋−1) $l = (\begin{matrix} n - 1 \\ ⌊ \frac{n}{2} ⌋ - 1 \end{matrix})$ and h=(n⌊n2⌋)−(n−2⌊n2⌋) $h = (\begin{matrix} n \\ ⌊ \frac{n}{2} ⌋ \end{matrix}) - (\begin{matrix} n - 2 \\ ⌊ \frac{n}{2} ⌋ \end{matrix})$ . The scheme has a white base matrix consisting of ℓ columns of all 1s and m − ℓ columns with all 0s, and a black base matrix consisting of all binary vectors with exactly [n/2] elements equal to 1.

For example, for n = 4, scheme S_D has m = 6, ℓ =3, and h = 5 and is given by:

M W = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 111111111111000000000000 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ M B = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ 110010101001011001010011 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ .

$\begin{matrix} M_{W} = [\begin{matrix} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \end{matrix}] & M_{B} = [\begin{matrix} 1 & 1 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 \end{matrix}] . \end{matrix}$

Let S be the (2, n, 0, 0,1)-VCS obtained applying Lemma 3 to scheme S_D. Scheme S is a canonical scheme, and the cardinality of the collections C_B and C_W is r = m. The values of the probabilities are p_b∣b = h/m, p_w∣b = 1 − h/m, p_{b| w} = ℓ/m, p_w|w = 1 − ℓ/m. Since S is canonical the scheme S′ obtained with Construction 1 is canonical. The value of the pixel expansion m′ can be arbitrarily fixed between 1 and r.

Consider the case of m′= 2. For such a value of m′ there are only two possible choices for the thresholds: ℓ′ = 0, h′= 1 or ℓ′ = 1 , h′ = 2. It is easy to see from the structure of M_W and M_B that the following two properties hold:

PW: For any set Q of two participants, the matrix MQW $M_{W}^{Q}$ consists of ℓ columns of 2 ones and m − ℓ columns of 2 zeroes.
PB: For any set Q of two participants, the matrix MQB $M_{B}^{Q}$ consists of S=(n−1⌊n2⌋) $S = (\begin{matrix} n - 1 \\ ⌊ \frac{n}{2} ⌋ \end{matrix})$ columns of 2 zeroes and m − s columns with at least a 1 (this is because for a qualified set Q of 2 participants matrix MQB $M_{B}^{Q}$ reconstructs a pixel with exactly h black subpixels, hence the remaining m − h = s are white).

Let us now determine the parameters of the resulting scheme in the two considered cases.

Case ℓ′ = 0, h′ = 1.

To compute p′b|b ${p^{'}}_{b | b}$ , consider that in this case a reconstructed pixel is black if at least one subpixel is black (and white otherwise). If a qualified set Q is fixed, by property PB, it is easy to see that the matrices of the collection CQB(S′) $C_{B}^{Q} (S^{'})$ that consists of all zeroes are exactly s(s − 1). Thus, P′w|b=s(s−1)m(m−1) ${P^{'}}_{w | b} = \frac{s (s - 1)}{m (m - 1)}$ and consequently P′b|b=1−s(s−1)m(m−1) ${P^{'}}_{b | b} = 1 - \frac{s (s - 1)}{m (m - 1)}$ .

To compute P′b|w ${P^{'}}_{b | w}$ , consider a qualified set Q. By property PW, the matrices of the collection CQW(S′) $C_{W}^{Q} (S^{'})$ that consists of all zeroes are exactly (m−ℓ)(m−ℓ−1). Hence, p′w|w=(m−l)(m−l−1)m(m−1) ${p^{'}}_{w | w} = \frac{(m - l) (m - l - 1)}{m (m - 1)}$ , which gives p′b|w=1−(m−ℓ)(m−ℓ−1)m(m−1) ${p^{'}}_{b | w} = 1 - \frac{(m - ℓ) (m - ℓ - 1)}{m (m - 1)}$ .

Hence, for the (2, n)-threshold scheme obtained by choosing ℓ′ = 0 the probabilistic factor is:

β 0 = ( m - ℓ ) ( m - ℓ - 1 ) - s ( s - 1 ) m ( m - 1 ) .

$β_{0} = \frac{(m - ℓ) (m - ℓ - 1) - s (s - 1)}{m (m - 1)} .$

Case ℓ′ = 1,h′ = 2.

To compute p′b|b ${p^{'}}_{b | b}$ , consider that in this case a reconstructed pixel is black if both subpixels are black (and white otherwise). If a qualified set Q is fixed, by property PB, the matrices of the collection CQB(S′) $C_{B}^{Q} (S^{'})$ that have at least a 1 in each column are exactly (m − s)(m − s − 1). Thus, p′b|b=(m−s)(m−s−1)m(m−1) ${p^{'}}_{b | b} = \frac{(m - s) (m - s - 1)}{m (m - 1)}$ .

To compute p′b|w ${p^{'}}_{b | w}$ , fix any qualified set Q and consider that by property PW, the matrices of the collection CQB(S′) $C_{B}^{Q} (S^{'})$ that have at least a 1 in each column are exactly ℓ(ℓ−1). Thus, p′b|w=l(l−1)m(m−1) ${p^{'}}_{b | w} = \frac{l (l - 1)}{m (m - 1)}$ .

Hence, for the (2, n)-threshold scheme obtained by choosing ℓ′ = 1 the probabilistic factor is:

β 1 = ( m - s ) ( m - s - 1 ) - ℓ ( ℓ - 1 ) m ( m - 1 ) .

$β_{1} = \frac{(m - s) (m - s - 1) - ℓ (ℓ - 1)}{m (m - 1)} .$

Compare now the value of β for the above two cases trying to figure out whether one case is better than the other, i.e., the probabilistic factor is bigger and a better quality image is reconstructed. It is possible to express the difference β₁ − β₀ as

β 1 - β 0 = ψ m ( s ) - ψ m ( ℓ ) m ( m - 1 )

$β_{1} - β_{0} = \frac{ψ_{m} (s) - ψ_{m} (ℓ)}{m (m - 1)}$

where ψ_m(x) = (m − x)(m − x − 1)+ x(x − 1). The first and second derivatives of ψ with respect to x are ∂2ψm∂x=4x−2m $\frac{\partial^{2} ψ_{m}}{\partial x} = 4 x - 2 m$ and ∂2ψm∂x2=4 $\frac{\partial^{2} ψ_{m}}{\partial x^{2}} = 4$ , respectively. Hence, function ψ_m(x) is a convex ∪ function of x, with a minimum at x = m/2. A simple algebra shows that, for n even, S=m4⋅n−2n−1 $S = \frac{m}{4} \cdot \frac{n - 2}{n - 1}$ and l=m2 $l = \frac{m}{2}$ and that for n odd, S=m4⋅n+1n $S = \frac{m}{4} \cdot \frac{n + 1}{n}$ and l=m2⋅n−1n $l = \frac{m}{2} \cdot \frac{n - 1}{n}$ . Since in both cases s < ℓ ≤ m/2, it is possible to conclude that ψ_m(s) > ψ_m(ℓ) and then β₁ > β₀. A simple analysis shows that the limit of β₁ as n approaches infinity is 5/16 ≃ 0.31, while the limit of β₀ as n approaches infinity is 3/16 ≃ 0.18.

In the case of any m′ Equations (5.2)–(5.5) can be used to compute the probabilities of probabilistic schemes, over all choices of ℓ′ and h′. Table 5.1 gives the resulting values of the probabilistic factor β of S′ over all possible choices of ℓ′ and m′, for the case of n. Since for n = 3 scheme S_D has m = 3 clearly for m′ = 3 we get a deterministic scheme; such a scheme is obtained for ℓ′ = 1, h′ = 2. It is worth to notice that for other choices of ℓ′ the probabilistic factor of the scheme is 0 meaning that no probabilistic scheme with pixel expansion m′ = 3 can be constructed with Construction 1. For the case of m′ = 2 ℓ′ = 1 and ℓ′ = 2 are valid choices and they both yield a 13 $\frac{1}{3}$ -probabilistic scheme.

Table 5.1 Values of β for scheme S′ for n = 3. The max over each row is in boldface.

m′ℓ′,h′	0,1	1,2	2,3
1	1/3	-	–
2	1/3	1/3	–
3	0	1	0

Table 5.2 Values of β for n = 4. The max over each row is in boldface.

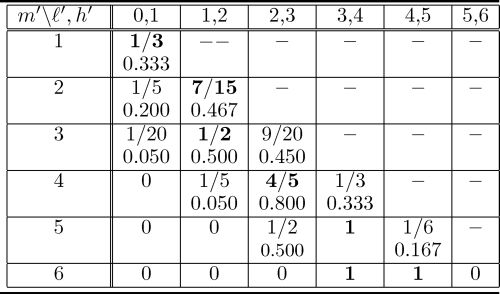
Images

Table 5.2 gives the resulting values of the probabilistic factor β of S′ over all possible choices of ℓ′ and m′, for the case of n = 4. Notice that for n = 4 scheme S_D has m = 6, hence, for m′ = 6 deterministic schemes can be obtained (in this case both ℓ′ = 3 and ℓ′ = 4 yield a deterministic scheme). As reported in the table, also for m′ = 5 a deterministic scheme can be obtained by choosing ℓ′ = 3. For the other possible choices of m′, the table shows in boldface the biggest probabilistic factor β found.

Finally, Table 5.3 gives the resulting values of the probabilistic factor β of S′ over all possible choices of ℓ′ and m′, for the case of n = 5. For n = 5 scheme S_D has m = 10, hence, m′ can range from 2 to 10. As reported in the table, a deterministic schemes is obtained from m′ = 8 (in such a case, by choosing ℓ′ = 4). Again the best probabilistic factor found is reported in boldface.

Table 5.3 Values of β for n = 5. The max over each row is in boldface and ϵ₁ and ϵ₂ denote very small values.

Images

5.7 Probabilistic Schemes with Boolean Operations

One of the peculiar characteristics of VCS is the fact that the reconstruction of the secret image is done via the human visual system. This means that representing a black pixel as ‘1’ and the white pixel as ‘0,’ the reconstruction is performed via an ”OR” operation of the superposed pixels contained in the shares. Relaxing such an assumption, it is possible to obtain diferent classes of VCS where the secret pixel is reconstructed after performing diferent boolean operations on the subpixels contained in the shares. For example XOR-based VCS have been proposed in [17]. As regards probabilistic VCS, several proposals have been done [20, 18, 8], where the basic operation for the reconstruction is no more based on the OR of the shared subpixels, and both the distribution and the reconstruction phases are consequently modified.

5.7.1 (2,n) Scheme for Binary Images (Wang)

In [20], Wang et al. proposed a probabilistic (2, n)-VCS based on binary XOR and AND operations, denoted with ⊗ and &, respectively. The construction is given in Figure 5.3.

Images

FIGURE 148.5
A construction for (2,n) Boolean probabilistic VCS.

In Wang’s scheme, a reverse coding of the pixel is adopted, assigning ‘0’ to black pixel and ‘1’ to white pixels. In this scheme it is easy to see that a black pixel in the secret image will be always mapped to a black pixel in each of the computed shares A_i because of the AND operation performed in the computation of the C_j (for a ‘0’ pixel, C_j = B_j&0 = 0) and the XOR operation in the reconstruction phase (the contribution for C_j = 0 means that A_j = B_n+1 ⊕ C_j = B_n+1 and then A′ = A_j ⊕ A_k = B_n+1 ⊕ B_n+1 = 0). The probabilities of reconstructing a black pixel are then p_b|b = 1 and p_w|b = 0. A white pixel will be reconstructed on the basis of the result of the XOR operation performed on the two matrices B_i and B_k, which are randomly selected. Then p_w|w = p_b|w = 1/2. Hence, the construction returns a β = 1/2 probabilistic scheme with contrast 1/2.

The above presented scheme has been modified by Ulutas et al. in [18] and Chang et al. in [8]. In the first work the construction is modified by adding a mechanism to augment the probability of selecting a white (black) pixel given that a white (black) pixel was present in the secret image. Basically, matrices B_i are no more randomly generated as in Wang’s scheme, but are selected in two different sets, one for white pixels and the other for black pixels, in order to maximize the probability of reconstructing a pixel of the right color. Then a random matrix R of the same size of the secret image is generated and used to compute the share. The reconstruction phase is not modified. The modified scheme is given in Figure 5.2.

In Chang et al’s construction, a voting strategy is adopted to apply the Wang method to grayscale images [8]. In such a method, for each original pixel, the binary representation of its grayscale value is considered, and for each bit composing the representation, the Wang scheme is executed and repeated 2m + 1 times in the generation phase. In the reconstruction phase, the voting method is used to recover the best result out of the shared bits in order to restore the original grayscale value of the pixel.

Images

FIGURE 5.2
Ulutas et al. [18] construction for (2,n) Boolean probabilistic VCS.

5.7.2 (n,n) Scheme for Binary Images (Wang)

A construction similar to the one above described, was proposed by Wang also for a (n,n) probabilistic VCS. The construction is given in Figure 9.6

Images

FIGURE 5.3
A construction for (n, n) Boolean probabilistic VCS.

In such a scheme it is easy to see that a black pixel in the secret image will be always mapped to a black pixel in each of the computed shares A_i because of the and operation performed in the computation of the C_j (for a ’0’ pixel, C_j = B_j & 0 = 0) and the XOR operation in the reconstruction phase (the contribution for C_j = 0 means that A_j = B_n+1 ⊕ C_j = B_n+1 and then A′ = A_j ⊕ A_k = B_n+1 ⊕ B_n+1 = 0. Then p_b∣b, = 1 and p_w∣b = 0. A white pixel will be reconstructed according to the pixel returned after the XOR between the two matrices B_i and B_k, which are randomly selected. Then p_w∣w = p_b∣w = 1/2. Hence, the construction returns a β =1/2 probabilistic scheme with contrast 1/2.

The same construction has been extended by Wang et al. in [21] to deal with grayscale images. Basically each pixel is coded with a binary string g − 1 bits long, where g denotes the gray level number, and having a number of ”1”s equivalent to the 1s present in the binary string obtained by the grey level g (without respecting the order). A pixel having grey level k in a range from 0 to g − 1, is represented by a binary string having g − k ’0’s and k − 1 ’1’s. The construction returns a probabilistic scheme with m = g − 1.

5.8 Conclusions and Open Problems

The probabilistic model for VCS schemes has been first described in Yang [22], where the reconstruction of the secret pixel has been given in probabilistic terms, no more guaranteeing the correctness property of the traditional VCS schemes. A generalization of the model has been given then in [11], where probabilistic schemes with pixel expansion have been described, showing that there is a one-to-one correspondence between probabilistic schemes with no pixel expansion and deterministic schemes and that such a one-to-one mapping trades the probabilistic nature of the scheme with the contrast of the deterministic scheme. Probabilistic schemes with pixel expansion can be obtained from deterministic schemes and their probabilistic factors can be studied. While for (n, n)-threshold schemes it has been proved that there is a linear relation between the pixel expansion and the probabilistic factor, for (2, n)-threshold schemes no closed expression for the probabilistic factor has been found. Finally, a probabilistic model has been extended and alternative operations (instead of OR) have been considered for the distribution of the shares and the reconstruction of the secret images.

Bibliography

[1] Ateniese G., Blundo C., De Santis A., and Stinson D. R. (1996). Visual cryptography for general access structures. Information and Computation, 129, 86–106.

[2] Ateniese G., Blundo C., De Santis A., and Stinson D. R. (1996). Constructions and bounds for visual cryptography. Proceedings of ICALP 1996, Paderbon, Germany, 8–12 July, pp. 416–428, Springer Verlag LNCS 1099.

[3] Ateniese G., Blundo C., De Santis A., and Stinson D. R. (2001). Extended schemes for visual cryptography. Theoretical Computer Science, 250, 143–161.

[4] Blundo C., D’Arco P., De Santis A., and Stinson D. R. (2003). Contrast optimal threshold visual cryptography schemes. SIAM J. on Discrete Mathematics, 16, 224–261.

[5] Blundo C., De Bonis A., and De Santis A. (2001). Improved schemes for visual cryptography. Designs, Codes, and Cryptography, 24, 255–278.

[6] Blundo C. and De Santis A. (1998). Visual cryptography schemes with perfect reconstruction of black pixels. Journal for Computers & Graphics, 22, 449–455.

[7] Blundo C., De Santis A., and Stinson D. R. (1999). On the contrast in visual cryptography schemes. Journal of Cryptology, 12, 261–289.

[8] Chang C., Lin C., Le T.H., and Le H.B. (2008). A probabilistic visual secret sharing scheme for grayscale images with voting strategy. Proceedings of the International Symposium on Electronic Commerce and Security, 2008, pp. 184–188.

[9] Cimato S., De Prisco R., and De Santis A. (2004). Colored visual cryptography without color darkening. In Proceedings of the 4th Conference on Security in Communication Networks, Amalfi, Italy, 8–10 September, pp. 236–251, Springer Verlag LNCS 3352.

[10] Cimato S., De Prisco R. and De Santis A. (2005), Optimal colored threshold visual cryptography schemes. Designs, Codes and Cryptography, 35, 311–335.

[11] Cimato S., De Prisco R., and De Santis A. (2006). Probabilistic visual cryptography schemes. The Computer Journal, 49(1), 97–107.

[12] Hofmeister T., Krause M. and Simon H. U. (2000). Contrast-optimal k out of n secret sharing schemes in visual cryptography. Theoretical Computer Science, 240, 471–485.

[13] Ito R., Kuwakado H., and Tanaka H. (1999). Image size invariant visual cryptography. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, E82A(10), 2172–2177.

[14] Krause M. and Simon H. U. (2003). Determining the optimal contrast for secret sharing schemes in visual cryptography. Combinatorics, Probability and Computing, 12, 285–299.

[15] Kuhlmann C. and Simon H. U. (2000). Construction of visual secret sharing schemes with almost optimal contrast. Proceedings of the 11th ACM-SIAM Symposium on Discrete Algorithms, San Francisco, USA, 9–11 January, pp. 262–272.

[16] Naor M. and Shamir A. (1994). Visual cryptography. Proceedings of Eurocrypt 94, Perugia, Italy, May 9–12, pp. 1–12, Springer Verlag LNCS 950.

[17] Tuyls P., Hollmann H.D.L., van Lint J.H., and Tolhuizen L. (2005). XOR-based visual cryptography schemes. Designs, Codes, and Cryptography, 37, 169–186.

[18] Ulutas M., Nabiyev V.V., Ulutas G., and Shamir A. (2009). A PVSS scheme based on Boolean operations with improved contrast. Proceedings of International Conference on Network and Service Security, Paris, 2009, pp. 1–5.

[19] Verheul E. R. and van Tilborg, H.C.A. (1997). Constructions and properties of k out of n visual secret: Sharing schemes. Designs, Codes, and Cryptography, 11, 179–196.

[20] Wang D., Zhang L., Ma N., and Li X. (2006). Two secret sharing schemes based on Boolean operations. Pattern Recognition 40(10), 2776–2785

[21] Wang D., Li X., Yi F., Daoshun Wang, Xiaobo, Li, and Feng, Yi (2007). Probabilistic (n, n) visual secret sharing scheme for grayscale images. In Information Security and Cryptology, Lecture Notes in Computer Science, Vol. 4990. Springer-Verlag, Berlin, pp. 192–200

[22] Yang C.N. (2004). New visual secret sharing schemes using probabilistic method. Pattern Recognition Letters, 25, 481–494.

[23] Yang C.N. and Chen T.S. (2005). Size-adjustable visual secret sharing schemes. IEEE Trans. Fundamentals, 88, 2471–2474.

[24] Yang C.N. and Chen T.S. (2005). Aspect ratio invariant visual secret sharing schemes with minimum pixel expansion. Pattern Recognition Letters, 26, 193–206.

[25] Yang C.N. and Laih C.S. (2000). New colored visual secret sharing schemes. Designs, Codes, and Cryptography, 20, 325–335.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for
5 Probabilistic Visual Cryptography Schemes

5

Probabilistic Visual Cryptography Schemes

CONTENTS

5.1 Introduction

5.2 Visual Cryptography Schemes

5.2.1 The Deterministic Model

5.2.2 The Probabilistic Model

5.3 Canonical Probabilistic Schemes

5.4 Probabilistic Schemes with No Pixel Expansion

5.5 Trading Pixel Expansion with Probabilities

5.5.1 Probabilistic Schemes with Given Pixel Expansion

5.6 Constructing Probabilistic Schemes

5.6.1 (n, n)-Threshold Probabilistic Schemes with Any Pixel Expansion

5.6.2 (2, n)-Threshold Probabilistic Schemes with Any Pixel Expansion

5.7 Probabilistic Schemes with Boolean Operations

5.7.1 (2,n) Scheme for Binary Images (Wang)

5.7.2 (n,n) Scheme for Binary Images (Wang)

5.8 Conclusions and Open Problems

Bibliography

Table of Contents for 5 Probabilistic Visual Cryptography Schemes

Create new playlist

Sign In

Sign Up

CONTENTS

Table of Contents for
5 Probabilistic Visual Cryptography Schemes