17 Two-Decoding-Option Image Sharing Method

An image secret sharing scheme (ISSS) divides a secret image into some shadow images (referred to as shadows) in a way that requires the shadows in a certain privileged coalitions for the secret reconstruction. However, the secret image cannot be revealed if they are not combined in the prescribed way. A typical ISSS is often a (k, n)-threshold scheme, where k is the threshold value to reveal the secret and n is the number of total shadows. One can reconstruct a secret image by k or more shadows, while he cannot conjecture any information from less than k shadows. There are two major categories in ISSS: one is the visual cryptography scheme (VCS) and the other is the polynomial-based ISSS (PISSS).

In the (k, n)-VCS, a secret image is encrypted into n shadows by expanding each secret pixel into m (the pixel expansion) subpixels. Notice that the difference between the pixel and the subpixel is that the ”pixel” denotes the secret pixel located in the secret image, and the ”subpixel” means the pixel located in shadows. Actually, the size of a subpixel is the same as that of the secret pixel. Therefore, shadows are, in general, expanded. Any k participants may photocopy their shadows on transparencies and stack them on an overhead projector to visually decode the secret through the human visual system (HVS) without hardware and computation. However, stacking k − 1 or fewer shadows will not gain any information. The first VCS encrypted a halftone (black-and-white) secret image into noise-like shadows [11]; subsequently, most VCSs were dedicated to reducing the pixel expansion [5, 7, 16, 17, 18, 2].

Indeed the visual quality of the VCS is poor, which comes from its intrinsic property using the OR-operation for decoding. Contrarily, the PISSS can recover the secret image without any distortion, while it needs the computation. By directly adopting Shamir’s secret sharing scheme [12], a (k, n)-ISSS takes the secret pixel as the constant term in (k − 1)-degree polynomials to share the secret. To gain small shadows, Thien and Lin used all coefficients in a (k − 1)-degree polynomial to generate shadows with size 1/k times to the secret image [13]. Afterwards, Wang and Su [15] further reduced the shadow size by using the Huffman code. Shadows in [13, 15] are noise-like, which shadows are often suspect to censors. It would be better to design a (k, n)-ISSS with the ability of steganography, i.e. shadows look like a cover image (a pre-selected meaningful image). Actually, we can construct a (k, n)-ISSS being provided with meaningful and meaningless shadows according to our need. Some (k, n)-ISSSs with meaningful shadows were proposed [14, 21, 8, 19, 1, 4, 6]. For example, two user-friendly (k, n)-ISSSs [14, 21] produced the shadow with a shrunken secret image on it. However, the portrait on shadows had already leaked the secret information, and thus this scheme is, strictly speaking, not a secret sharing scheme. Other (k, n)-ISSSs [8, 19, 1, 4] can present any cover images on shadows. Lin and Tsai’s scheme [8] had the authentication capability to detect the faked shadows. The schemes in [19, 1, 4] improved Lin and Tsai’s scheme to solve the dishonest participant problem of authentication, enhance the detection ratio of manipulated shadows, and improve the visual qualities of shadows.

A new type of ISSS with two decoding options was introduced recently, where the secret image is revealed both by stacking the transparencies and by computation. This scheme is referred to as two-in-one ISSS (TiOISSS). TiOISSS can decode secret images for preview by the HVS when a computer is temporarily unavailable. When the computer is available during the decoding scene, we then spend more computation to obtain a high-quality image for high-end applications. Two TiOISSSs [6, 9] have been proposed. Both schemes can stack shadows to decode a halftone secret image by the HVS in the first stage, and then can perfectly reconstruct the gray-level secret image in the second stage. A possible application scenario of TiOISSS is described below. In a distributed multimedia system, n shadows of PISSS can be delivered in a distributed system where each shadow is stored in any distributed storage node. The failure of (n − k) shadows during transmission does not affect the reconstruction phase, as the secret image can be perfectly restored using k shadows. Suppose a fake shadow is received. The receiver spends considerable computation and finally finds the received shadow is wrong. Because the reconstruction phase of PISSS is very computationally intensive, we can apply the TiOISSS to save the computational time for verifying the validity of shadows. The receiver can first verify the shadows by visually previewing the secret without computation. After the successful verification, the receiver then recovers the original gray-level secret image by computation. In this chapter, we will briefly describe two TiOISSSs [6, 9], and also introduce our recent research result on TiOISSS published in [20].

17.2 Preliminaries

17.2.1 PISSS

A polynomial-based (k, n) secret sharing scheme was first proposed by Shamir [12], in which the secret data is encrypted into n shadows. Any k shadows can be used to reconstruct the secret, but any k − 1 or fewer shadows learn no information. By taking the secret data as g₀ (constant term) in the following (k − 1)-degree polynomial g(x) where p is a prime number, we could construct n shadows (x_i.g(x_i)) by choosing n different x_i, i ∈ [1, n].

g (x) = (g_{0} + g_{1} x + \dots + g_{k - 1} x_{k - 1}) \mod p . (17.1)

$g (x) = (g_{0} + g_{1} x + \dots + g_{k - 1} x_{k - 1}) \mod p . (17.1)$

Any k shadows (without loss of generality, we use k shadows (x_i. g(x_i)). i ∈ [1. k]) can be used to reconstruct the (k − 1)-degree polynomial g(x) by Lagrange interpolation as follows. Afterwards, the secret data g₀ can be determined from g₀ = g(0).

\begin{array}{l} g (x) = g (x_{1}) \frac{(x - x_{2}) (x - x_{3}) \dots (x - x_{k})}{(x_{1} - x_{2}) (x_{1} - x_{3}) \dots (x_{1} - x_{k})} \\ + g (x_{2}) \frac{(x - x_{1}) (x - x_{3}) \dots (x - x_{k})}{(x_{2} - x_{1}) (x_{2} - x_{3}) \dots (x_{2} - x_{k})} \\ + \dots + g (x_{k}) \frac{(x - x_{1}) (x - x_{2}) \dots (x - x_{k - 1})}{(x_{k} - x_{1}) (x_{k} - x_{2}) \dots (x_{k} - x_{k - 1})} \mod p . \end{array} (17.2)

$\begin{array}{l} g (x) = g (x_{1}) \frac{(x - x_{2}) (x - x_{3}) \dots (x - x_{k})}{(x_{1} - x_{2}) (x_{1} - x_{3}) \dots (x_{1} - x_{k})} \\ + g (x_{2}) \frac{(x - x_{1}) (x - x_{3}) \dots (x - x_{k})}{(x_{2} - x_{1}) (x_{2} - x_{3}) \dots (x_{2} - x_{k})} \\ + \dots + g (x_{k}) \frac{(x - x_{1}) (x - x_{2}) \dots (x - x_{k - 1})}{(x_{k} - x_{1}) (x_{k} - x_{2}) \dots (x_{k} - x_{k - 1})} \mod p . \end{array} (17.2)$

Through Shamir’s secret sharing scheme, we could take every secret pixel as g₀ in a (k − 1)-degree polynomial g(x) to construct n random grayscale values in shadows to construct a (k. n)-PISSS. At this time, the prime number p = 251 is chosen such that g(x) is constrained between 0 and 250 and suitable to represent the conventional 8-bit grayscale or color images. Notice that the possible values of an 8-bit gray pixel are from 0 to 255, so the grayscale values (> 250) need to be modified to 250 and will cause distortion. Obviously, we can use the Galois Field GF(2⁸) rather than the ordinary arithmetic (mod 251) to achieve a lossless scheme. Thien and Lin further reduced shadows with size 1/k times that of the secret image [13] by embedding the secret data in all coefficients of g(x). The formal encoding of Thien and Lin’s scheme is briefly described below.

A secret image is first divided into τ non-overlapping k-pixel blocks, and every j-th (0 ≤ j ≤τ − 1) block includes the secret pixel values Pjk.Pjk+1.⋯, Pjk+k−1. The (k − 1)-degree polynomial S_j(x) represents a shadow pixel associated with the j-th block on shadows.

S_{j} (x) = (p_{j k} + p_{j k + 1} x + p_{j k + 2} x^{2} + \dots + p_{j k + k - 1} x^{k - 1}) in G F (2^{8}), (17.3)

$S_{j} (x) = (p_{j k} + p_{j k + 1} x + p_{j k + 2} x^{2} + \dots + p_{j k + k - 1} x^{k - 1}) in G F (2^{8}), (17.3)$

where x is often an image identification and 0 ≤ j ≤ τ − 1. The value of S_j(x) is generated using the original pixel values p_jk.p_jk+₁,⋯,p_jk+k₋₁ included in the j-th block. In this chapter, the Galois Field GF(2⁸) was chosen to achieve a lossless secret image. Because k pixels are processed each time, the size of the shadow image is 1/k of the secret image. By reversing the encoding, the polynomial in (17.3) can be reconstructed from k shadow pixels; hence, the blocks can be recovered and finally the secret image is reconstructed.

17.2.2 VCS

The first VCS was Naor–Shamir’s (k. n)-VCS to encrypt a halftone secret image into noise-like shadows. The authors used the whiteness (the number of white subpixels in a m-subpixel block) to distinguish the black color from the white color, i.e., ”m − h”B”h”W (respectively ”m − l”B”l”W) represents a white (respectively black) color, where h > l. A black-and-white (k, n)-VCS can be designed using two base n × m matrices B₁ and B₀ with elements ”1” and ”0” denoting black and white subpixels. When sharing a black (respectively white) secret pixel, the dealer randomly chooses one row of the matrix in the set C₁ (respectively C₀), which includes all matrices obtained by permuting the columns in B₁ (respectively B₀) to a relative shadow. Let OR (B_i|r), i = 0.1, denote the ”OR”-ed vector of any r rows in B_i, and H(·) be the Hamming weight of a vector. The base matrices of the (k. n)-VCS should satisfy the following conditions:

(V-1). H (OR(B₁|r)) ≥ (m − l) and H (OR (B₀|r)) ≤ (m − h)) for r = k, where 0 ≤ l < h ≤ m.

(V-2). H (OR (B₁|r)) = H (OR (B₀|r)) for r ≤ (k − 1).

The first condition is often referred to as the contrast condition, and the secret image can be recognized due to their different contrasts of black and white colors. The second condition is the security condition that assures the (k, n)-VCS of perfect secrecy.

Example 1. Construct a (2, 2)-VCS of h =1, l = 0, and m = 2 using $B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}]$ $B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}]$ and $B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}]$ $B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}]$ . The secret is a printed-text image .

A (2, 2)-VCS with $B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}]$ $B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}]$ and $B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}]$ $B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}]$ has H(OR (B₁|2)) = 2, H(OR(B₀|2)) = 1, and H(OR(B₁|1)) = H(OR(B₀|1)) = 1, which satisfy (V-1) and (V-2) conditions. In the reconstructed image, the black color is 2B0W and the white color is 1B1W (or 1W1B). However, each shadow contains 1B1W and 1W1B with the same frequencies so that one cannot see anything from his own shadow. Figure 17.1(a) is a black-and-white secret image . Two noise-like shadows (Shadow 1, Shadow 2) and the reconstructed image by stacking two shadows (Shadow 1 + Shadow 2) are shown in Figures 17.1(b), 17.1(c) and 17.1(d). The printed-text secret can be revealed by HVS. □

Images

FIGURE 17.1
A (2, 2)-VCS of h = 1, l = 0, and m = 2: (a) the secret image (b) and (c) two shadows (d) the reconstructed image.

17.3 Previous Works

Two TiOISSSs [6, 9] are briefly reviewed in the sequel. Jin and Lin’s scheme [6] applied VCS on a halftone secret image, which is obtained from a prescribed halftoning transformation. Lin and Lin’s scheme [9] combined the VCS and PISSS. Both TiOISSSs have stacking-to-see capability. By computation, both schemes could reconstruct the original gray-level secret image. The TiOISSSs in this chapter can be extended to share the chromatic secret image by applying the approaches on C (cyan), M (magenta), and Y (yellow) bit planes, respectively. So, we only discuss the gray-level secret image.

17.3.1 Jin et al.’s TiOISSS

In [6], the gray-level secret image is transformed into a binary image by a digital halftoning method, in which every secret pixel is represented by nine black-and-white pixels (p_c, p₀, p₁, ⋯,p₇) in a 3 × 3-block as shown. Excluding the center pixel p_c, every 8-tuple (p_c, p₀, p₁, ⋯,p₇) is uniquely decoded to the 256 possible grayscale values (0 to 255), and simultaneously the pattern of nine pixels can simulate shades of gray. This halftoning method is most similar to a patterning technique, which uses the black dots in a block to represent the intensity levels. The color of the center pixel p_c can be chosen according to the halftone version of the original grayscale image to enhance the resolution. Afterwards, the (k, n)-VCS is performed on this halftone secret image to construct n shadows. Suppose the gray-level secret image and the halftone images are I and I′. We first obtain I′ from I by the halftoning technique (see Table in [6], which provides the complete mapping between I and I′, also gives the nine grayscale levels in I to simulate the grayscale levels), and then arrange the pixels in a 3 × 3-block. Thus, we have |I′| = 9 × |I|. Apply a (k, n)-VCS with the pixel expansion m on I′, and then every shadow of Jin et al’s TiOISSS has the image size 9 × m × |I| . Jin et al’s TiOISSS has two decoding options. The first is stacking any k out of n shadows to get a vague halftone image by VCS, and the second is to reconstruct the gray-level secret image by a look-up table from the arrangement of (p₀, p₁, ⋯,p₇).

Because we have two secret images (I and I′), we herein define the pixel expansion of TiOISSS as the ratio of shadow size relative to the size of the original gray-level secret image. So, the pixel expansion of Jin et al’s (k, n)-TiOISSS is

m_{J I N} = 9 m . (17.4)

$m_{J I N} = 9 m . (17.4)$

17.3.2 Lin and Lin’s TiOISSS

Jin et al.’s TiOISS scheme has a terrible pixel expansion 9m. For example, Jin et al.’s (2, 2)-TiOISS has the pixel expansion 9m = 18 when using (2, 2)-VCS with m = 2. Recently, Lin and Lin proposed a TiOISSS [9] based on the VCS and PISSS to reduce the pixel expansion. A halftone secret image is encrypted into n shadows by (k, n)-VCS with the pixel expansion m, which every row contains b ”1” and w ”0” and m = b + w. It is obvious that every m-subpixel has $(\begin{matrix} m \\ w \end{matrix})$ $(\begin{matrix} m \\ w \end{matrix})$ combinations, and it can be used to represent about $\log_{2} (\begin{matrix} m \\ w \end{matrix})$ $\log_{2} (\begin{matrix} m \\ w \end{matrix})$ bits. Notice that in the conventional VCS, we can randomly permute all m columns in matrices. However, when using the $(\begin{matrix} m \\ w \end{matrix})$ $(\begin{matrix} m \\ w \end{matrix})$ combinations to represent the information and simultaneously satisfy the security condition, we could only randomly choose the combination for one shadow and the remaining (n − 1) shadows are then determined according to the base matrices. Therefore, in a shadow, only (|I′|/n) digits can be used to share $\log_{2} (\begin{matrix} m \\ w \end{matrix})$ $\log_{2} (\begin{matrix} m \\ w \end{matrix})$ bits. On the other hand, we need (8 × |I|/k) bits to share the gray-level secret image I by (k, n)-PISSS. To assure we have enough space to hide the secret, the gray-level secret image is compressed by Jpeg or other compression techniques to reduce the information as (8 × |I|/(k × R)) bits where R is the compression ratio. In [9], the authors consider the case in which the halftone secret image and the gray-level secret image have the same size, i.e., |I| = |I′|.

As a result, $(| I^{'} | / n) \times \log_{2} (\begin{matrix} m \\ w \end{matrix}) \geq (8 \times | I | / (k \times R)),$ $(| I^{'} | / n) \times \log_{2} (\begin{matrix} m \\ w \end{matrix}) \geq (8 \times | I | / (k \times R)),$ and thus the compression ration R should satisfy the following requirement to hide all information of a gray-level secret image.

R \geq (8 n / k \times \log_{2} (\begin{array}{l} m \\ w \end{array})) (17.5)

$R \geq (8 n / k \times \log_{2} (\begin{array}{l} m \\ w \end{array})) (17.5)$

Since |I| = |I′|, finally, the pixel expansion of Lin and Lin’s (k, n)-TiOISSS is

m_{L I N}^{(C)} = m . (17.6)

$m_{L I N}^{(C)} = m . (17.6)$

For example, the pixel expansion of Lin and Lin’s (2, 2)-TiOISSS when using (2, 2)-VCS with m = 2 is $m_{L I N}^{(C)} = 2$ $m_{L I N}^{(C)} = 2$ less than m_JIN = 18. However, the gray-level secret image can be perfectly reconstructed in Jin and Lin’s scheme, while Lin and Lin’s scheme only recovers the compressed image. The greater compression ratio will degrade the visual quality of the secret image.

Example 2. Construct Lin and Lin’s (2, 4)-TiOISSS and Jin and Lin’s (2, 4)-TiOISSS using $\begin{matrix} B_{1} = [\begin{matrix} 1100 \\ 0110 \\ 0011 \\ 1001 \end{matrix}] & and & B_{0} = [\begin{matrix} 1100 \\ 1100 \\ 1100 \\ 1100 \end{matrix}] \end{matrix}$ $\begin{matrix} B_{1} = [\begin{matrix} 1100 \\ 0110 \\ 0011 \\ 1001 \end{matrix}] & and & B_{0} = [\begin{matrix} 1100 \\ 1100 \\ 1100 \\ 1100 \end{matrix}] \end{matrix}$ .

Since $(\begin{matrix} m \\ w \end{matrix}) = (\begin{matrix} 4 \\ 2 \end{matrix}) = 6$ $(\begin{matrix} m \\ w \end{matrix}) = (\begin{matrix} 4 \\ 2 \end{matrix}) = 6$ (there are six combinations: (1100), (0011), (1010), (0101), (1001), (0110)) $\log_{2} (\begin{matrix} m \\ w \end{matrix}) = \log_{2} 6 = 2.585$ $\log_{2} (\begin{matrix} m \\ w \end{matrix}) = \log_{2} 6 = 2.585$ bits. Suppose the secret image I is a 512 512 gray-level image. Lin and Lin’s TiOISS (2, 4) scheme needs a compression ratio $R = (8 n / k \times \log_{2} (\begin{matrix} m \\ w \end{matrix})) = 32 / (2 \times 2.585) = 6.19$ $R = (8 n / k \times \log_{2} (\begin{matrix} m \\ w \end{matrix})) = 32 / (2 \times 2.585) = 6.19$ . We first compress the gray-level secret image I to a compressed image I_C to obtain the less embedded bits. Notice that even though |I_C | has a lesser file size (the embedded bits), it has the same physical size of the original image |I|. Finally, the shadow size of Lin and Lin’s (2, 4)-TiOISSS is 1024 1024 (note: m × |I′|), and the pixel expansion is $m_{L I N}^{(C)} = m = 4$ $m_{L I N}^{(C)} = m = 4$ . On the other hand, we need a 1536 × 1536(9 × |I|) halftone image for Jin et al.’s (2, 4)-TiOISSS. The shadow size of Jin et al.’s (2, 4)-TiOISSS is 3072 × 3072(9m × |I|), and the pixel expansion is m_JIN = 9m = 36. □

17.4 A New (k, n)-TiOISSS

The VCS and PISSS have their respective features. As is known, the VCS has the vague reconstructed image and PISSS has a perfect reconstruction. The VCS has the distinctive stacking-to-see capability, while PISSS spends the computation for reconstruction. It is reasonable to adopt the stacking-to-see property of the VCS into PISSS to achieve a two-in-one scheme where the secret image is revealed both by stacking the transparencies and by computation. Our new TiOISSS [20] is also a combination of the VCS and PISSS, which is somewhat similar to Lin and Lin’s scheme, but the way is completely different to that in Lin and Lin’s scheme.

Jin et al.’s TiOISSS is a lossless version (i.e., no distortion in the secret image) but has a large pixel expansion. Lin and Lin’s TiOISSS is a compressible version. It compresses the secret image such that the shadow size has enough space to hide the information of a compressed image. Although Lin and Lin’s scheme reduces the pixel expansion of Jin et al.’s scheme, the reconstructed image has distortion. Obviously, Lin and Lin’s approach can be extended to the lossless version by expanding the halftone image with the size $| I^{'} | = (n / k) \times | I | \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix})$ $| I^{'} | = (n / k) \times | I | \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix})$ to hide the original secret image. For the lossless version of Lin and Lin’s TiOISSS, the pixel expansion $m_{L I N}^{(L)}$ $m_{L I N}^{(L)}$ is

m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) . (17.7)

$m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) . (17.7)$

For example, the pixel expansion of Lin and Lin’s (2, 4)-TiOISSS in Example 2 (i.e. k = n = 2, m = 4, w = 2) is $m_{L I N}^{(L)} = 24.76$ $m_{L I N}^{(L)} = 24.76$ .

Jin et al.’s scheme cannot be used in a compressible version because it uses a look-up table to recover the grayscale value of the pixel. The proposed TiOISSS has two versions—the lossless version and the compressible version. For simplicity, we first describe the proposed TiOISSS, which reconstructs a lossless secret image. The compressible version is just an easy extension of the lossless TiOISSS, and will be discussed in Section 17.4.2.

17.4.1 Design Concept

Our design concept adopts the gray subpixel into the VCS, and this grayscale values simultaneously represents the output of the (k − 1)-degree polynomial in PISSS. In VCS, it is evident that when a subpixel is stacked by the white subpixel, its intensity is kept unchanged. While stacking two gray subpixels, we get a grayer color (a dark version of the color). Therefore, if we replace black subpixels with gray subpixels in the shadow, we still can use the whiteness in every m subpixel to distinguish the black color from the white color in the reconstructed image. Here, we adopt the widely accepted definition of color superimposition in [10] to define the color mixing function C(•) when stacking two subpixels with the grayscale values between 0 and 255.

The grey level of the resultant pixel by stacking the two pixels can be expressed (approximately) as follows, in which each mixed color is produced by a color mixing function C(•).

g_{3} = C (g_{1}, g_{2}) = Int ((g_{1} \times g_{2}) / 255),

$g_{3} = C (g_{1}, g_{2}) = Int ((g_{1} \times g_{2}) / 255),$

where Int(•) function maps a real number to the nearest integer. The values of g₁, g₂, g₃ are any grayscale values between 0 and 255, and ”0” (respectively ”255”) is a black (respectively, white) color.

It is easy to verify g₃ < g₁ and g₃ < g₂, and this implies that stacking two gray pixels of g₁ and g₂ results in a grayer pixel of g₃. For example, g₁ = C(g₁, 255) shows the grayscale value unchanged when stacking with the white pixel and 255 = C(255, 255) shows that the stacked result is a white color when stacking two white pixels.

Example 3. Consider Example 1, and randomly use gray subpixels g_i ∈ [0, 255] instead of black subpixels in B1 and B0 and do not change the white subpixel.

As a replacement in B₁ and B₀, we have ${B^{'}}_{1} = [\begin{matrix} g_{i} 0 \\ 0 g_{j} \end{matrix}]$ ${B^{'}}_{1} = [\begin{matrix} g_{i} 0 \\ 0 g_{j} \end{matrix}]$ and ${B^{'}}_{0} = [\begin{matrix} g_{i} 0 \\ g_{j} 0 \end{matrix}]$ ${B^{'}}_{0} = [\begin{matrix} g_{i} 0 \\ g_{j} 0 \end{matrix}]$ , respectively. In the reconstructed image, it is observed that the stacked result in the black area (using B′₁ ) is 1g_i1g_j and the stacked result in the white area (using B′₀) is 1g_k 1W or 1W1g_k, where g_k < g_i and g_k < g_j. Through the whiteness, we can still visually reveal the secret. Each shadow contains 1g_i1W (or 1W1g_i) which is a gray-and-white and noise-like image, so that one cannot see anything from any shadow. In Figure 17.2(a) and Figure 17.2(b) are two noise-like shadows (Shadow 1, Shadow 2) and Figure 17.2(c) shows the reconstructed image (Shadow 1 + Shadow 2). It is observed that the secret is also revealed but is a little blurred when compared with Figure 17.1(d). □

We call this VCS with the matrices and B0 the gray-subpixel based VCS (GVCS). Matrices B′₁ and B′₀ are the same as B₁ and B₀ except that the gray subpixels replaced the black subpixels. Hence, GVCS holds the contrast and security conditions (V-1) and (V-2), and it is still a VCS. In this chapter, we use the notation (k, n, m, g)-GVCS, to denote a (k, n)-GVCS with ${B^{'}}_{1}$ ${B^{'}}_{1}$ and ${B^{'}}_{0}$ ${B^{'}}_{0}$ , in which every row has g gray subpixels and (m − g) white subpixels. The whiteness, (m − g) white subpixels in every m-subpixel block, can be used to distinguish the black color from the white color. In GVCS, the grayness of the nonwhite subpixels in the reconstructed image is different from the pure blackness in the VCS, and it will distort the clarity (see Figure 17.1(d) and Figure 17.2(c)).

Images

FIGURE 17.2
A (2, 2)-GVCS of h = 1, l = 0, and m = 2: (a) and (b) two shadows (c) the reconstructed image.

In order to design a TiOISSS based on GVCS and PISSS, we should carefully observe the distinguishing characteristics of both image secret sharing schemes. All characteristics of GVCS and PISSS are opposite; hence, combining GVCS and PISSS creates the following problem. It is obvious that we need two secret images—a halftone secret image for GVCS and a gray-level secret image for PISSS. In our TiOISSS, the gray-level secret image is shared by PISSS. Then, we divide the halftone secret image into shadows by GVCS, in which the grayscale values in ${B^{'}}_{1}$ ${B^{'}}_{1}$ and ${B^{'}}_{0}$ ${B^{'}}_{0}$ are chosen according to the outputs of the (k − 1)-degree polynomials in PISSS. Also, we need to determine the sizes of both secret images such that there are enough gray subpixels in GVCS to represent the outputs of PISSS.

17.4.2 The Lossless TiOISSS

We construct a (k, n)-TiOISSS based on a (k, n)-PISSS and a (k, n, m, g)-GVCS to share a gray-level secret image I. For the lossless version, we first determine (8 × |I|/k) bits by PISSS. So, |I|/k gray supixels in each shadow of (k, n, m, g)-GVCS are required to hide (8 × |I|/k) bits. Since there are g gray subpixels in every m subpixels of (k, n, m, g)-GVCS, the halftone secret image I′ for GVCS should be |I′| = |I|/(k × g). So, the shadow size is m × |I′|. For the lossless version, the pixel expansion of our (k, n)-TiOISSS $m_{P R O}^{(L)}$ $m_{P R O}^{(L)}$ is

m_{P R O}^{(L)} = m / (k \times g) . (17.8)

$m_{P R O}^{(L)} = m / (k \times g) . (17.8)$

The formal encoding and decoding algorithms are described as follows. Some notations are defined first.

Notation Used

P(•) encryption of (k, n)-PISSS.

P⁻¹ (·) decryption of (k, n)-PISS.

I the gray-level secret image with the size |I|, which is used as the input of P(•).

P_i the output shadows of P(I), i ∈ [1, n], with the size (|I|/k).

G(•) encryption of (k, n, m, g)-GVCS with ${B^{'}}_{1}$ ${B^{'}}_{1}$ and ${B^{'}}_{0}$ ${B^{'}}_{0}$ , and the values of gray subpixels are chosen according to the gray pixels in P_i.

G⁻¹(•) decryption of (k, n, m, g)-GVCS (stack shadows and visually decode the secret by HVS).

H(•) halftoning function, transform and resize a gray-level image to a halftone image.

I′ a halftone secret image with the size |I′| = |I|/(k × w) obtained from I′ = H(I).

G_i the output shadows of G(I′), i ∈ [1, n], with the size ((m × |I|)/(k x g)).

Encryption Algorithm of the Lossless Version of Our (k, n)-TiOISSS

Input: the gray-level secret image I; the parameters k, n, m, g; matrices ${B^{'}}_{1}$ ${B^{'}}_{1}$ and ${B^{'}}_{0}$ ${B^{'}}_{0}$ .

Output: n shadows G_i, i ∈ [1, n].

1-1) Encrypt the secret image to obtain P_i= P(I), i ∈ [1, n].

1-2) Obtain I′ from I′ = H(I).

1-3) Output n shadows G_i=G(I′), i ∈ [1, n].

Decryption Algorithm of the Lossless Version of Our (k, n)-TiOISSS

Input: any k out of n shadows $G_{i_{1}}, G_{i_{2}}, \dots, G_{i_{k}}$ $G_{i_{1}}, G_{i_{2}}, \dots, G_{i_{k}}$ .

Output: the halftone secret image I′ (Phase 1); the gray-level secret image I (Phase 2).

/* Phase 1: does not need computation; visually decode the secret I′ by stacking k shadows;

Phase 2: needs computation; decode the secret I by using Lagrange interpolation */

Phase 1 (preview phase):

^2-1) $G^{- 1} (G_{i_{1}}, G_{i_{2}}, \dots, G_{i_{k}})$ $G^{- 1} (G_{i_{1}}, G_{i_{2}}, \dots, G_{i_{k}})$ ^;

/* stack k shadows to visually preview the halftone secret image */

Phase 2 (perfect-reconstruction phase):

2-2) Obtain $(P_{i_{1}}, P_{i_{2}}, \dots, P_{i_{k}})$ $(P_{i_{1}}, P_{i_{2}}, \dots, P_{i_{k}})$ from $(G_{i_{1}}, G_{i_{2}}, \dots, G_{i_{k}})$ $(G_{i_{1}}, G_{i_{2}}, \dots, G_{i_{k}})$ by discarding the white subpixels.

2-3) $I = P^{- 1} (P_{i_{1}}, P_{i_{2}}, \dots, P_{i_{k}})$ $I = P^{- 1} (P_{i_{1}}, P_{i_{2}}, \dots, P_{i_{k}})$ .

/* use Lagrange interpolation to reconstruct the gray-level secret image */

Our TiOISSS contains two decoding phases: the preview phase and the perfect-reconstruction phase. A halftone secret image can be visually previewed by simply stacking shadows in Phase 1. The preview phase may be used when a computer is temporarily not available, or in a scenario verifying whether the shadows are correct or not in a distributed multimedia system, as mentioned in the introduction. On the other hand, by extracting the gray subpixels from shadows we may perfectly reconstruct the gray-level secret image when the computer finally is available (or after successful verification in a distributed multimedia system). We call the second decoding phase the perfect-reconstruction phase because we can gain a lossless secret image.

Considering security, the proposed (k, n)-TiOISSS is a combination of two (k, n)-threshold schemes: the GVCS and the PISSS. So our scheme still retains the threshold property. An attacker could not stack less than k shadows to retrieve the black-and-white secret. Also, he cannot use the gray values of less than k shadows to reconstruct the (k − 1)-degree polynomial. Thus, combining these two ISSSs together assures the secrecy of the threshold scheme.

Example 4 shows the proposed (2, 2)-TiOISSSs using different w and m to demonstrate different shadow sizes and the resolutions of the reconstructed images in the preview phase.

Example 4. Construct two (2, 2)-TiOISSSs using base matrices: (1) $\begin{matrix} B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}] & and & B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}] \end{matrix}$ $\begin{matrix} B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}] & and & B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}] \end{matrix}$ (2) $\begin{matrix} B_{1} = [\begin{matrix} 110 \\ 101 \end{matrix}] & and & B_{0} = [\begin{matrix} 110 \\ 110 \end{matrix}] \end{matrix}$ $\begin{matrix} B_{1} = [\begin{matrix} 110 \\ 101 \end{matrix}] & and & B_{0} = [\begin{matrix} 110 \\ 110 \end{matrix}] \end{matrix}$ , respectively. The secret image is 512 × 512 Lena from the USC-SIPI image database.

A 512 × 512 gray-level Lena image I is shown in Figure 17.3(a). By (2, 2)-PISSS, we obtain two 512 × 256 gray-level noise-like shadows P₁ and P₂, as shown in Figure 17.3(b) and Figure 17.3(c).

Case (1) $\begin{matrix} B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}] & and & B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}] \end{matrix}$ $\begin{matrix} B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}] & and & B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}] \end{matrix}$ :

Since m = 2 and g = 1, we then resize and halftone I to get a halftone image I′ by H(•), and the size is |I′| = |I|/(k × g) = |I|/2. This 512 × 256 halftone Lena is shown in Figure 17.4(a). Output two shadows G_i=G(I′), i = 1, 2, by using (2, 2, 2, 1)-GVCS, and the values of gray subpixels are chosen according to the gray pixels in P₁ and P₂. In Figure 17.4(b) and Figure 17.4(c) are two gray-and-white shadows G₁ and G₂ of the size m × |I′| = |I| (512 × 512-pixels). Figure 17.4(d) is the previewed image by stacking G₁ and G₂ without computation. In the second phase of decoding, we can obtain P₁ and P₂ from the gray pixels of G₁ and G₂, and then reconstruct the gray-level Lena in Figure 17.4(a) by I = P⁻¹(P₁, P₂).

Images

FIGURE 475.17
A (2, 2)-PISSS: (a) 512 × 512 gray-level Lena secret image (b) and (c) 512 × 256 gray-level noise-like shadows.

Images

FIGURE 476.17
The proposed (2, 2)-TiOISSS using base matrices with h = 1, l = 0, and m = 2: (a) 512 × 256 halftone image (b) and (c) two 512 × 512 gray-and-white shadows (d) the previewed image.

Images

FIGURE 17.5
The proposed (2, 2)-TiOISSS using base matrices with h = 1, l = 0, and m = 3: (a) and (b) two 512 × 512 gray-and-white shadows (c) the previewed image.

Case (2) B_{1} = [\begin{matrix} 110 \\ 101 \end{matrix}], B_{0} = [\begin{matrix} 110 \\ 110 \end{matrix}] :

$Case (2) B_{1} = [\begin{matrix} 110 \\ 101 \end{matrix}], B_{0} = [\begin{matrix} 110 \\ 110 \end{matrix}] :$

Since m = 3 and g = 2, we need a halftone image I′ of the size is |I′| = |I|/(k × g) = |I|/4. Output two shadows G_i = G(I′), i =1, 2, by using (2, 2, 3, 2)-GVCS, and the values of gray subpixels are chosen according to the gray pixels in P₁ and P₂. In Figure 17.5(a) and Figure 17.5(b) are two gray-and-white shadows G₁ and G₂ of the size m × |I′| = 0.75 × |I| (512 × 384-pixels). Figure 17.5(c) is the stacked result by stacking G₁ and G₂. By the same approach in Case (1), we can also reconstruct the original gray-level Lena I. □

All the above schemes can visually reveal the secret by simply stacking shadows in the preview phase. The original gray-level secret image can be perfectly reconstructed in the perfect-reconstruction phase. Of two (2, 2)-TiOISSSs in Example 4, Figure 17.4(d) possess the better resolution of the previewed result, but Figure 17.5(c) has a lesser shadow size of 512 × 384 pixels.

Because our TiOISSS uses PISSS in Phase 2 for decoding, we can use the compression approach in [9] to hide the compressed image into shadows. Suppose J(•) is a Jpeg-compression function, where I_C =J(I), and the compression ratio is R = (the number of bits in I/the number of bits in I_C) ≥ 1. At this time, the gray-level secret image I is compressed to I_C such that the information bits in I_C can be embedded into the halftone secret image I′. By replacing I with I_C in our lossless TiOISSS, we could get the compressible TiOISSS. The formal encoding/decoding algorithm of the compressible version of our (k, n)-TiOISSS is omitted for brevity.

In the lossless version of the proposed TiOISSS, since |I′| = |I|/(k × g), k ≥ 2 and g ≥ 1, then |I′| < |I|. This observation implies that our TiOISSS could embed all information bits of lossless I into I′, where |I′| < |I|, for any values of (k, n, m, g). So, actually, our TiOISSS does not need compression on I. However, to be fairly compared with the compressible version of Lin and Lin’s scheme, we use a compression ratio $R = R_{L I N} = (n / k) \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix})$ $R = R_{L I N} = (n / k) \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix})$ such that we have the same image quality of the reconstructed image (a Jpeg-compressed version) as Lin and Lin’s scheme; at this time the size of our halftone secret image can be further reduced to |I′| = |I|/(k × g × R). Then, the shadow size is m × |I′| = (m × |I|/(k × g × R)) and the pixel expansion of the compressible version $m_{P R O}^{(C)}$ $m_{P R O}^{(C)}$ is

m_{P R O}^{(C)} = m / (k \times g \times R) . (17.9)

$m_{P R O}^{(C)} = m / (k \times g \times R) . (17.9)$

17.5 Experimental Results and Comparisons

Example 5 shows three (2, 4)-TiOISSSs, Jin et al.’s scheme [6], Lin and Lin’s scheme [9] and our scheme [20], respectively; this example demonstrates the lossless version. The compressible versions of Lin and Lin’s (2, 4)-TiOISSS and our (2, 4)-TiOISSS are given in Example 6, where a compression ratio $R = 6.5 > R_{L I N} = (4 / 2) \times 8 / \log_{2} (\begin{matrix} 4 \\ 2 \end{matrix}) = 6.19$ $R = 6.5 > R_{L I N} = (4 / 2) \times 8 / \log_{2} (\begin{matrix} 4 \\ 2 \end{matrix}) = 6.19$ is used.

Example 5. Construct three lossless versions of (2, 4)-TiOISSSs: (1) Jin et al.’s scheme (2) Lin and Lin’s scheme (3) our scheme (the lossless version) using $B_{1} = [\begin{matrix} 1100 \\ 0110 \\ 0011 \\ 1001 \end{matrix}]$ $B_{1} = [\begin{matrix} 1100 \\ 0110 \\ 0011 \\ 1001 \end{matrix}]$ and $B_{0} = [\begin{matrix} 1100 \\ 1100 \\ 1100 \\ 1100 \end{matrix}]$ $B_{0} = [\begin{matrix} 1100 \\ 1100 \\ 1100 \\ 1100 \end{matrix}]$ .

A 512 × 512 gray-level Lena in Figure 17.3(a) is used as a secret image. By (2, 4)-PISSS, we first obtain four 512 × 256 gray-level shadows P₁ − P₄. To share all information bits in P_i, Jin et al’s scheme and Lin and Lin’s scheme need the 1274 × 1274 halftone secret image and the 1536 × 1536 halftone image, while our scheme needs the 256 × 256 halftone secret image (since k = g = 2, so |I′| = |I|/(k × g) = |I|/4). The shadow sizes of Jin et al.’s scheme, Lin and Lin’s scheme and our scheme are 3072 × 3072 pixels, 2548 × 2548 pixels and 512 × 512 pixels, respectively. Finally the pixel expansions are m_JIN = (3072 × 3072)/(512 × 512) = 36, $m_{L I N}^{(L)} = (2548 \times 2548) / (512 \times 512) = 24.76$ $m_{L I N}^{(L)} = (2548 \times 2548) / (512 \times 512) = 24.76$ and $m_{P R O}^{(L)} = (512 \times 512) / (512 \times 512) = 1$ $m_{P R O}^{(L)} = (512 \times 512) / (512 \times 512) = 1$ . □

Example 6. Consider Lin and Lin’s scheme and our scheme in Example 5 but use the compressible versions with a compression ratio R = 6.5.

By J(•), we compress the original Lena into the compressed image I_C with PSNR = 38.88 dB. Now, Lin and Lin’s (2, 4)-TiOISSS has enough space in I′ (|I′| = |I|) to embed the information of I_C. By using I_C as the original gray-level secret image in our TiOISSS, we only need the 201 × 201 halftone secret images for sharing information bits. For the compression version, the pixel expansions of (2, 4)-TiOISSS are $m_{L I N}^{(C)} = m = 4$ $m_{L I N}^{(C)} = m = 4$ and $m_{P R O}^{(C)} = m / (k \times g \times R) = 1 / R = 1 / 6.5 = 0.154$ $m_{P R O}^{(C)} = m / (k \times g \times R) = 1 / R = 1 / 6.5 = 0.154$ . □

When comparing the pixel expansions among these three TiOISSSs [6, 9, 20], we consider the lossless version. This is a fair approach since all three schemes can reconstruct the same quality of the reconstructed image. From Equations (17.4), (17.7), and (17.8), it is obvious that our pixel expansion $m_{P R O}^{(L)} < m_{J I N}$ $m_{P R O}^{(L)} < m_{J I N}$ (since k ≥ 2 and g ≥ 1, so m/(k × g) < m/2 < 9m). When comparing $m_{L I N}^{(L)}$ $m_{L I N}^{(L)}$ and $m_{P R O}^{(L)}$ $m_{P R O}^{(L)}$ , one can verify that our TiOISSS has the lesser pixel expansion than Lin and Lin’s TiOISSS for most values of k, n, and m. In the following theorem, we theoretically prove that $m_{P R O}^{(L)} < m_{L I N}^{(L)}$ $m_{P R O}^{(L)} < m_{L I N}^{(L)}$ when both TiOISSSs use Naor-Shamir optimal (n, n)-VCS, Naor-Shamir optimal (3, n)-VCS, and Naor-Shamir (2, n)-VCS [11].

Theorem: The pixel expansion $m_{P R O}^{(L)} = m / (k \times g)$ $m_{P R O}^{(L)} = m / (k \times g)$ of the proposed (k, n)-TiOISSS is lesser than the pixel expansion $m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix})$ $m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix})$ of Lin and Lin’s TiOISSS when using Naor-Shamir optimal (n, n)-VCS, Naor-Shamir optimal (3, n)-VCS, and Naor-Shamir (2, n)-VCS.

Proof: When using Naor-Shamir optimal (n, n)-VCS (note: k = n) with m = 2⁽ⁿ⁻¹⁾, w = g = m/2, we have

\begin{array}{l} m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) = m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) \\ = 8 m / \log_{2} (\frac{m!}{(m / 2)! \times (m / 2)!}) = 8 m / \log_{2} (\frac{m \times (m - 1) \times \dots \times (m / 2 + 1)}{(m / 2) \times (m / 2 - 1) \times \dots \times 1}) \\ > 8 m / \log_{2} (m^{m / 2}) = 8 m / ((m / 2) \times \log_{2} (m)) = 16 / (\log_{2} (2^{(n - 1)})) \\ = 2^{4} / (n - 1) > 2 / n = m / (k \times g) = m_{P R O}^{(L)} (since g = m / 2 and k = n) . \end{array} (17.10)

$\begin{array}{l} m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) = m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) \\ = 8 m / \log_{2} (\frac{m!}{(m / 2)! \times (m / 2)!}) = 8 m / \log_{2} (\frac{m \times (m - 1) \times \dots \times (m / 2 + 1)}{(m / 2) \times (m / 2 - 1) \times \dots \times 1}) \\ > 8 m / \log_{2} (m^{m / 2}) = 8 m / ((m / 2) \times \log_{2} (m)) = 16 / (\log_{2} (2^{(n - 1)})) \\ = 2^{4} / (n - 1) > 2 / n = m / (k \times g) = m_{P R O}^{(L)} (since g = m / 2 and k = n) . \end{array} (17.10)$

When using Naor-Shamir (3, n)-VCS with m = 2n − 2, w = 0 = m/2, we have

\begin{array}{l} m_{L I N}^{(L)} = (n / 3) \times m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) = ((8 \times m \times n) / 3) / \log_{2} (\begin{matrix} m \\ m / 2 \end{matrix}) \\ = ((8 \times m \times n) / 3) / \log_{2} (\frac{m \times (m - 1) \times \dots \times (m / 2 + 1)}{(m / 2) \times (m / 2 - 1) \times \dots \times 1}) \\ > ((8 \times m \times n) / 3) / \log_{2} (m^{m / 2}) = (16 n / 3) / \log_{2} (m) = (16 n / 3) / \\ (\log_{2} (2 n - 2)) \\ > ((4 n - 4) / 3) / (\log_{2} (2 n - 2)) = (2 / 3) \times (2 n - 2) / (\log (2 n - 2)) \\ > 2 / 3 = m / (k \times g) = m_{P R O}^{(L)} (since g = m / 2 and k = 3) . \end{array} (17.11)

$\begin{array}{l} m_{L I N}^{(L)} = (n / 3) \times m \times 8 / \log_{2} (\begin{array}{l} m \\ w \end{array}) = ((8 \times m \times n) / 3) / \log_{2} (\begin{matrix} m \\ m / 2 \end{matrix}) \\ = ((8 \times m \times n) / 3) / \log_{2} (\frac{m \times (m - 1) \times \dots \times (m / 2 + 1)}{(m / 2) \times (m / 2 - 1) \times \dots \times 1}) \\ > ((8 \times m \times n) / 3) / \log_{2} (m^{m / 2}) = (16 n / 3) / \log_{2} (m) = (16 n / 3) / \\ (\log_{2} (2 n - 2)) \\ > ((4 n - 4) / 3) / (\log_{2} (2 n - 2)) = (2 / 3) \times (2 n - 2) / (\log (2 n - 2)) \\ > 2 / 3 = m / (k \times g) = m_{P R O}^{(L)} (since g = m / 2 and k = 3) . \end{array} (17.11)$

When using Naor-Shamir (2, n)-VCS with m = n, w = m − 1, g = 1, we have

\begin{array}{l} m_{L I N}^{(L)} = (n / 2) \times m \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix}) = (4 \times m \times m) / \log_{2} (\begin{matrix} m \\ m - 1 \end{matrix}) \\ = (4 m^{2}) / \log_{2} (m) = (4 m) (m / \log_{2} (m)) > 4 m \\ > m / 2 = m / (k \times g) = m_{P R O}^{(L)} (since g = 1 and k = 2) . \end{array} (17.12)

$\begin{array}{l} m_{L I N}^{(L)} = (n / 2) \times m \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix}) = (4 \times m \times m) / \log_{2} (\begin{matrix} m \\ m - 1 \end{matrix}) \\ = (4 m^{2}) / \log_{2} (m) = (4 m) (m / \log_{2} (m)) > 4 m \\ > m / 2 = m / (k \times g) = m_{P R O}^{(L)} (since g = 1 and k = 2) . \end{array} (17.12)$

From Equations (17.10), (17.11), and (17.12), we obtain $m_{L I N}^{(L)} > m_{P R O}^{(L)}$ $m_{L I N}^{(L)} > m_{P R O}^{(L)}$ . The proof is completed.

Table 17.1 lists the pixel expansions of some (k, n)-TiOISSSs. Our scheme (respectively, Lin and Lin’s scheme) could choose different g (respectively, w) in the same m to reduce the shadow size. For exampl, both (2, 2)-TiOISSSs can use $B_{1} = [\begin{matrix} 110 \\ 101 \end{matrix}], B_{0} = [\begin{matrix} 110 \\ 110 \end{matrix}]$ $B_{1} = [\begin{matrix} 110 \\ 101 \end{matrix}], B_{0} = [\begin{matrix} 110 \\ 110 \end{matrix}]$ instead of $B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}], B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}]$ $B_{1} = [\begin{matrix} 10 \\ 01 \end{matrix}], B_{0} = [\begin{matrix} 10 \\ 10 \end{matrix}]$ to reduce the pixel expansions from $m_{P R O}^{(L)} = 1$ $m_{P R O}^{(L)} = 1$ and $m_{L I N}^{(L)} = 16$ $m_{L I N}^{(L)} = 16$ to $m_{P R O}^{(L)} = 3 / 4$ $m_{P R O}^{(L)} = 3 / 4$ and $m_{L I N}^{(L)} = 15.14$ $m_{L I N}^{(L)} = 15.14$ , respectively. Our (2, 3)-TiOISSS could reduce the pixel expansion from 3/2 to 3/4 by replacing $B_{1} = [\begin{matrix} 100 \\ 010 \\ 001 \end{matrix}], B_{0} = [\begin{matrix} 100 \\ 100 \\ 100 \end{matrix}]$ $B_{1} = [\begin{matrix} 100 \\ 010 \\ 001 \end{matrix}], B_{0} = [\begin{matrix} 100 \\ 100 \\ 100 \end{matrix}]$ with $B_{1} = [\begin{matrix} 110 \\ 011 \\ 101 \end{matrix}], B_{0} [\begin{matrix} 110 \\ 110 \\ 110 \end{matrix}]$ $B_{1} = [\begin{matrix} 110 \\ 011 \\ 101 \end{matrix}], B_{0} [\begin{matrix} 110 \\ 110 \\ 110 \end{matrix}]$ , but the pixel expansion $m_{P R O}^{(L)} = 22.71$ $m_{P R O}^{(L)} = 22.71$ of Lin and Lin’s scheme cannot be further reduced since $(\begin{matrix} m \\ w \end{matrix}) = (\begin{matrix} 3 \\ 2 \end{matrix}) = (\begin{matrix} 3 \\ 1 \end{matrix})$ $(\begin{matrix} m \\ w \end{matrix}) = (\begin{matrix} 3 \\ 2 \end{matrix}) = (\begin{matrix} 3 \\ 1 \end{matrix})$ . Our pixel expansions $m_{P R O}^{(L)} = m / (k \times g)$ $m_{P R O}^{(L)} = m / (k \times g)$ when using Naor-Shamir (2, n)-VCS, (3, n)-VCS and (n, n)-VCS, are n/2, 2/3 and 2/n, respectively. From Equations (17.4), (17.7), and (17.8), it is observed that $m_{L I N}^{(L)}$ $m_{L I N}^{(L)}$ is n-intensive and the value will increase when n increases whereas the other two schemes are n-invariant. On the other hand, Lin and Lin’s scheme and our scheme obtain more effective performance for large k than Jin et al.’s scheme because their pixel expansions are inversely proportional to the value of k.

File sizes of shadows in Table 17.1 are represented in bits when using a 512 × 512 gray-level secret image. The values in parentheses imply that we send the raw data (use one bit ”1” (or ”0”) denoting the black (or white) color) to transmit the black-and-white shadows for Jin et al.’s scheme and Lin and Lin’s scheme. For example, when using the bitmap file format, the number of bits per pixel, which is the color depth of the image, typically can be 1, 4, 8, 16, 24, and 32. Even though both schemes use the color depth 1, our TiOISSS (use the color depth 8) still has the lesser file sizes of shadows for all cases in Table 17.1. For example, the file sizes of shadows for Jin et al.’s (3, 6)-TiOISSS and Lin and Lin’s (3, 6)-TiOISSS are 23592960 bits (≈23.6 Mbits) and 5258608 bits (≈5.3 Mbits) when using one bit to represent the color, while our (3, 6)-TiOISSS just needs only 1398101 bits (≈1.4 M Kbits) when using 8 bits to represent the color to transmit a gray-and-white shadow. Notice that when all schemes are using the same file format of the color depth 8, Jin et al.’s (3, 6)-TiOISSS and Lin and Lin’s (3, 6)-TiOISSS require 188743680 bits (≈188.7 Mbits) and 42068864 bits (≈42.1 Mbits), respectively, which are significantly larger than 1.4Mbits.

By the contrast definition ((h − 1)/(m + l)) of VCS in [3], the contrasts of the previewed images are calculated and shown. Since the previewed image is used for verification in a distributed multimedia system; therefore, our primary task is to choose the suitable m and g to obtain the reduced shadow size to make the transmission and storage more efficient.

To elucidate on the good results of the proposed scheme among the existing TiOISSSs, some properties are evaluated: (1) the resolution of the reconstructed image, (2) the decoding complexity, (3) the shadow images (including the image pattern, the shadow size, the file size of shadow), and (4) the pixel expansion. A comparison among three TiOISSSs in [6, 9, 20] is listed in Table 17.2. All three schemes have dual modes of decoding—one for preview (or when a computer is temporarily unavailable) and the other for perfectly reconstructing the original gray-level secret image. Also, they all have a distinctive stacking-to-see property. Our scheme and Lin and Lin’s scheme use Lagrange interpolation for perfect reconstruction with the computational complexity O(k) and no additional memory space, while Jin et al.’s scheme uses a 8 × 8 ROM lookup table for reconstruction without computation. Our gray-and-white shadows have the benefit of reducing the physical size and the file size of the shadow when compared with other two TiOISSSs.

17.6 Conclusion

Our TiOISSS is a hybrid—half is the VCS and half is PISSS—with each specialties employed: the easy decoding of the VCS in Phase 1 and the perfect reconstruction of PISSS in Phase 2. Our combination of the VCS and PISSS is different from that in Lin and Lin’s TiOISSS [9]. Lin and Lin use the combinations in the m-subpixel block to represent the output value of PISSS, while the value is embedded into GVCS to construct our TiOISSS. Finally, our scheme reduces the shadow size and the file size of the shadow.

Table 17.1 Pixel expansions, file sizes of shadows, and contrasts of the previewed images for some (k, n)-TiOISSSs

Images

#1: $m_{J I N} = 9 m # 2 : m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix}) # 3 : m_{P R O}^{(L)} = m / (k \times g) # 4 : contrast = ((h - l) / (m + l))$ $m_{J I N} = 9 m # 2 : m_{L I N}^{(L)} = (n / k) \times m \times 8 / \log_{2} (\begin{matrix} m \\ w \end{matrix}) # 3 : m_{P R O}^{(L)} = m / (k \times g) # 4 : contrast = ((h - l) / (m + l))$

#5: Naor-Shamir (2, n)-VCS #6: Naor-Shamir (3, n)-VCS #7: Naor-Shamir (n, n)-VCS

Table 17.2 A comparison among three TiOISSSs.

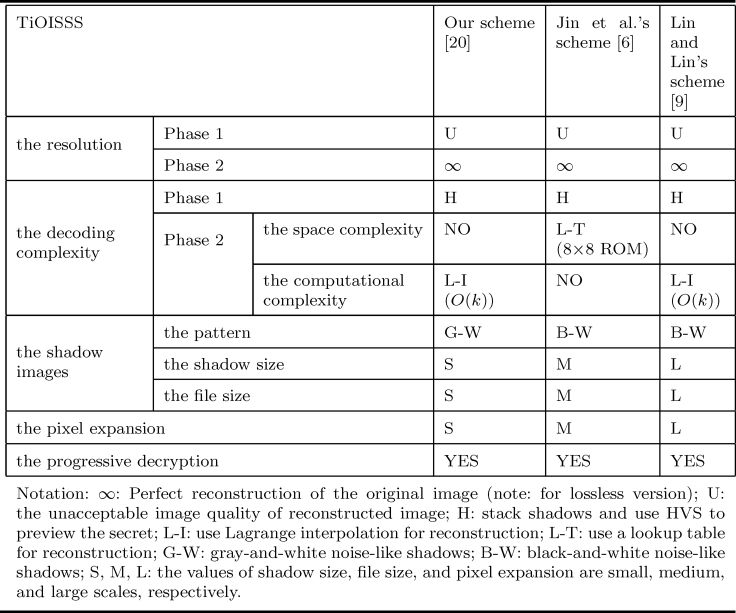
Images

Notation: ∞: Perfect reconstruction of the original image (note: for lossless version); U: the unacceptable image quality of reconstructed image; H: stack shadows and use HVS to preview the secret; L-I: use Lagrange interpolation for reconstruction; L-T: use a lookup table for reconstruction; G-W: gray-and-white noise-like shadows; B-W: black-and-white noise-like shadows; S, M, L: the values of shadow size, file size, and pixel expansion are small, medium, and large scales, respectively.

Bibliography

[1] C.C. Chang, Y.P. Hsieh, and C.H. Lin. Sharing secrets in stego images with authentication. Pattern Recognition, 41:3130–3137, 2008.

[2] S. Cimato, R. De Prisco, and A. De Santis. Probabilistic visual cryptography schemes. The Computer Journal, 49:97–107, 2006.

[3] P.A. Eisen and D.R. Stinson. Threshold visual cryptography schemes with specified whiteness. Designs, Codes and Cryptography, 25:15–61, 2002.

[4] Z. Eslami, S.H. Razzaghi, and J.Z. Ahmadabadi. Secret image sharing based on cellular automata and steganography. Pattern Recognition, 43:397–404, 2010.

[5] R. Ito, H. Kuwakado, and H. Tanaka. Image size invariant visual cryptography. IEICE Trans. on Fund. of Elect. Comm. and Comp. Sci., E82-A:2172–2177, 1999.

[6] D. Jin, W.Q. Yan, and M.S. Kankanhalli. Progressive color visual cryptography. Journal of Electronic Imaging, 14:033019–033113, 2005.

[7] H. Kuwakado and H. Tanaka. Size-reduced visual secret sharing scheme. IEICE Trans. on Fund. of Elect. Comm. and Comp. Sci., E87-A:1193–1197, 2004.

[8] C.C. Lin and W.H. Tsai. Secret image sharing with steganography and authentication. Journal of Systems & Software, 73:405–414, 2004.

[9] S.J. Lin and J.C. Lin. VCPSS: A two-in-one two-decoding-options image sharing method combining visual cryptography (VC) and polynomial-style sharing (PSS) approaches. Pattern Recognition, 40:3652–3666, 2007.

[10] F. Liu, C.K. Wu, and X.J. Lin. Color visual cryptography schemes. IET Information Security, 2:151–165, 2009.

[11] M. Naor and A. Shamir. Visual cryptography. In Advances in Cryptology-EUROCRYPT94 LNCS 950, pages 1–12, 1994.

[12] A. Shamir. How to share a secret. Communications of the Association for Computing Machinery, 22:612–613, 1979.

[13] C.C. Thien and J.C. Lin. Secret image sharing. Computers & Graphics, 26:765–770, 2002.

[14] C.C. Thien and J.C. Lin. An image-sharing method with user-friendly shadow images. IEEE Trans. on Circ. and Sys. for Video Tech., 13:1161–1169, 2003.

[15] R.Z. Wang and C.H. Su. Secret image sharing with smaller shadow images. Pattern Recognition Letters, 27:551–555, 2006.

[16] C.N. Yang. New visual secret sharing schemes using probabilistic method. Pattern Recognition Letters, 25:481–494, 2004.

[17] C.N. Yang and T.S. Chen. Size-adjustable visual secret sharing schemes. IEICE Trans. on Fund. of Elect. Comm. and Comp. Sci., E88-A:2471–2474, 2005.

[18] C.N. Yang and T.S. Chen. New size-reduced visual secret sharing schemes with half reduction of shadow size. IEICE Trans. on Fund. of Elect, Comm. and Comp. Sci., E89-A:620–625, 2006.

[19] C.N. Yang, T.S. Chen, K.H. Yu, and C.C. Wang. Improvements of image sharing with steganography and authentication. Journal of Systems & Software, 80:1070–1076, 2007.

[20] C.N. Yang and C.B. Ciou. Image secret sharing method with two-decoding-options: lossless recovery and previewing capability. Image and Vision Computing, 28:1600–1610, 2010.

[21] C.N. Yang, K.H. Yu, and R. Lukac. User-friendly image sharing using polynomials with different primes. International Journal of Imaging Systems and Technology, 17:40–47, 2007.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for
17 Two-Decoding-Option Image Sharing Method

17

Two-Decoding-Option Image Sharing Method

CONTENTS

17.1 Introduction

17.2 Preliminaries

17.2.1 PISSS

17.2.2 VCS

17.3 Previous Works

17.3.1 Jin et al.’s TiOISSS

17.3.2 Lin and Lin’s TiOISSS

17.4 A New (k, n)-TiOISSS

17.4.1 Design Concept

17.4.2 The Lossless TiOISSS

17.5 Experimental Results and Comparisons

17.6 Conclusion

Bibliography

Table of Contents for 17 Two-Decoding-Option Image Sharing Method

Create new playlist

Sign In

Sign Up

CONTENTS

Table of Contents for
17 Two-Decoding-Option Image Sharing Method