11 Resolving the Alignment Problem in Visual Cryptography

The basic principle of the Visual Cryptography Scheme (VCS) was first formally introduced by Naor and Shamir [10]. The idea of the VCS proposed in [10] is to split an image into two random shares (printed on transparencies), which separately reveal no information about the original secret image other than the size of the secret image. The image is composed of black and white pixels. The original image can be recovered by stacking the two transparencies together.

One important parameter in VCS is pixel expansion, where the pixel expansion reflects the size of the recovered secret image. Many papers in the literature are dedicated to proposing VCS with smaller pixel expansion. However, all these works are based at the pixel level, i.e., to reduce the number of subpixels that represent a pixel of the original secret image.

We notice that, the final goal of reducing the pixel expansion is to reduce the size of the transparencies that are distributed to the participants, because smaller transparencies are easier to transport. However, the size of the subpixels that are printed on the transparencies affects the final size of the transparencies; in fact, the size of the transparencies is the product of the size of the subpixels and the number of the subpixels in each transparency. Unfortunately, there is a dilemma when one tries to determine the size of the subpixels: When the subpixel size is large, it is easy to align the shares (most publications in the literature require aligning the shares precisely in the decrypting phase), but the large subpixel size will result in large transparencies. On the other hand, when the subpixel size is small, it is relatively hard to align the shares, but smaller transparencies result. From the point of view of the participants of the VCS, the goal is to align the shares easily and have small transparencies as well. Table 11.1 shows the relationship between the size of the subpixels of the transparencies and the ease to align them (more comparisons will be given in Table 11.5 later). Hence, there is a trade-off between the size of the subpixels of the transparencies and the ease to align them.

Table 11.1 The advantages and disadvantages of large and small subpixels.

size of the subpixels	advantages	disadvantages
larger	easier to align	larger transparency size
smaller	smaller transparency size	harder to align

The usual way of tackling the alignment problem of the VCS is by adding frames to the shares. To align the shares one just needs to align the frames. Yan et al. [13] employed the Walsh transform to embed marks in both of the shares so as to find the alignment position of these shares. However, both methods need to align the transparencies precisely. Besides, Kobara and Imai [6] considered a different problem. They calculated the visible space when viewing the transparencies. The results are somehow related to the alignment problem, but not exactly, as [6] has no discussion about alignment at all. Kobara and Imai [6] do not consider the stacking of more than two shares. Nakajima and Yamaguchi [9] proposed a (2, 2), extended VCS, which the secret image and shares are natural images. Their scheme can simultaneously reduce the alignment difficulty. However, their scheme does not hold the perfect security like a secret sharing scheme.

In fact, the precise alignment of small subpixels is not critical. The secret image can still be recovered visually even if the participants do not align the transparencies precisely. This phenomenon helps to determine the size of the subpixels printed on the transparencies.

This chapter focuses on some recent results about the alignment problem of the visual cryptography scheme [8, 16]. Two kinds of alignment problems of share images are considered. First, the share images are misaligned by integer number of subpixels (less than the pixel expansion). This part mainly comes from [8]. In such a case, the secret image can still be observed as its complementary image. Second, the share images are misaligned by less than one subpixel. This part mainly comes from [16]). Conditions that the secret image can still be recovered are studied, and the different misalignment tolerances of large and small subpixels are compared. The results indicate that the VCS, by itself, has some misalignment tolerance. At last, we provide a misalignment tolerant VCS based on the trade-off between the usage of large and small subpixels.

11.2 Preliminaries

In the VCS, there is a secret image that is encrypted into some shares. The secret image is called the original secret image for clarity, and the shares are the encrypted images (and are called the transparencies if they are printed). When a qualified set of shares (transparencies) are stacked together, it gives a visual image that is almost the same as the original secret image, we call it the recovered secret image. In the case of black and white images, the original secret image is represented as a pattern of black and white pixels. Each of these pixels is divided into subpixels, which themselves are encoded as black and white to produce the shares. The recovered secret image is also a pattern of black and white subpixels that should visually reveal the original secret image if a qualified set of shares is stacked.

In order to simplify the discussion, in this paper, we will only consider the black and white VCS, where black pixels are denoted by 1 and white pixels are denoted by 0.

By a (k, n)-VCS we mean a scheme where the original secret image is divided into n shares, which are distributed to n participants. Any subgroup of k out of these n participants can get a recovered secret image, but any subgroup consisting of less than k participants does not have any information other than the size about the original secret image.

For a vector v ∈ GF^m(2), we denote by w(v) the Hamming weight of the vector v, i.e., the number of nonzero coordinates in v. A (k, n)-VCS, denoted by (C₀,Cı), consists of two collections of n × m binary matrices C₀ and C₁. To share a white (resp. black) pixel, a dealer (the one who sets up the system) randomly chooses one of the matrices, called a share matrix, in C₀ (resp. C₁) and distributes its rows (representing a pattern of subpixels in the share) to the n participants of the scheme, giving row i to participant i, i = 1, …, n. More precisely, we give a formal definition of the (k, n)-VCS as follows:

Definition 1 Let k, n, m be nonnegative integers, l and h be positive numbers satisfying 2 ≤ k ≤ n and 0 ≤ l < h ≤ m. The two collections of n × m binary matrices (C₀,C₁) constitute a visual cryptography scheme (k, n)-VCS if the following properties are satisfied:

(Contrast) For any s ∈ C₀, the OR of any k out of n rows of s is a vector v that satisfies w(v) ≤ l.
(Contrast) For any s ∈ C₁, the OR of any k out of n rows of s is a vector v that satisfies w(v) ≥ h.
(Security) For any i₁ < i₂ < … < i_t in {1,2, … ,n} with t < k, the two collections of t × m matrices D_j, j = 0, 1, obtained by restricting each n×m matrix in C_j, j = 0, 1, to rows i₁, i₂ … i_t, are indistinguishable in the sense that they contain the same matrices with the same frequencies.

Note that, in the above definition,

m is called the block length and determines the pixel expansion of the scheme. A pixel of the original secret image is represented by m subpixels in the recovered secret image. In general, we are interested in schemes with m being as small as possible. h and l are called the darkness thresholds of the black and white pixels, respectively.
Define the value α=h−lm $α = \frac{h - l}{m}$ to be the contrast of the scheme. Note that, however, there are other definitions of the contrast of VCS. We use this definition to establish our result. The proof is similar for other definitions of contrast.

We consider VCS in which C₀, C₁ are constructed from a pair of n × m binary matrices M₀, M₁, called basis matrices. The set C_i, i = 0,1 consists of the m! matrices obtained by applying all permutations to the columns of M_i. This approach of VCS construction will have small memory requirements (it only keeps the basis matrices) and high efficiency (to choose a matrix in C₀ (resp. C₁) as it only needs to generate a permutation of the basis matrix). We will use the basis matrices to simplify the discussions.

The above definition of VCS is also called the Deterministic Visual Cryptography Scheme (DVCS). The original secret image can be deterministically recovered by the qualified shares pixel by pixel in such schemes. In contrast to the DVCS, Yang and Cimato et al. proposed the Probabilistic Visual Cryptography Scheme (PVCS) in [14, 4], where the pixels of the original secret image can only be probabilistically recovered by the qualified shares, however, in the overall view the original secret image can be recovered visually as well.

Definition 2 (Probabilistic VCS [14, 4]) Let k, n, and m be nonnegative integers, I and h be positive numbers, satisfying 2 ≤ k ≤ n and 0 ≤ l < h ≤ m . The two collections of n x m binary matrices (Co,Ci) constitute a probabilistic threshold Visual Cryptography Scheme (k, n)-PVCS if the following properties are satisfied:

(Contrast) For the collection C₀ and a share matrix s ∈ C₀, by v a vector resulting from the OR of any k out of the n rows of s. If w(v) denotes the average of the Hamming weights of v, over all the share matrices in C₀, then w¯¯¯(υ)≤l¯ $\bar{w} (υ) \leq \bar{l}$ .
(Contrast) For the collection C₁, the value of w¯¯¯(υ) $\bar{w} (υ)$ satisfies w¯¯¯(υ)≥h¯ $\bar{w} (υ) \geq \bar{h}$ .
(Security) For any i₁ < i₂ < … < i_t in {1, 2, … ,n} with t < k, the two collections of t × m′ matrices D_j, j = 0, 1, obtained by restricting each n × m′ matrix in C_j, j = 0, 1, to rows i₁, i₂, … i_t are indistinguishable in the sense that they contain the same matrices with the same frequencies.

The definition of PVCS in [14] only considers the case with n × 1 share matrices, we extend their definition to the n × m′ case. And the definition of PVCS in [4] used the factor ß to reflect the contrast, we use the values l¯ $\bar{l}$ and h¯ $\bar{h}$ (darkness grey-levels) to reflect the contrast. The same point of the three definitions of PVCS is that, for a particular pixel in the original secret image, the qualified participants can only correctly represent it in the recovered secret image with a certain probability. Because the human eyes always average the high frequency black and white dots into gray areas, so the average value of the Hamming weight of the black dots in the area reflects the grayness of the area. The PVCS does not require the satisfaction of the difference in grayness for each pixel in the recovered secret image as the DVCS does. It only reflects the difference in grayness in the overall view.

The contrast of the DVCS is fulfilled for each pixel (consisting of m sub-pixels) in the recovered secret image, however, this is quite different in the PVCS. The application of the average contrast, denoted by α¯¯ $\bar{α}$ , first appeared in [3]. This term is often used in the PVCS, see [4, 14, 11, 7], where the traditional contrast of the PVCS does not exist. Here we define the average contrast to be the average value of the overall contrast of the recovered secret image, i.e., the mean value of the contrast of all the pixels in the recovered secret image. According to our definition of the contrast α=h−lm $α = \frac{h - l}{m}$ , the average contrast can be calculated by the formula α¯¯=h¯−l¯m′ $\bar{α} = \frac{\bar{h} - \bar{l}}{m^{'}}$ , where h and l¯ $\bar{l}$ are the mean values of w(v) for the black and white pixels in the overall recovered secret image respectively, and m′ is the pixel expansion of the PVCS. Because the number of pixels is large in the recovered secret image, the values h¯ $\bar{h}$ and l¯ $\bar{l}$ are equivalent to the mean values of the w(v) in the collections C₁ and C₀, respectively. Note that, the DVCS also has the average contrast, and many proposed DVCS’s in the literature have α¯¯=α $\bar{α} = α$ , see examples in [10, 5, 1], etc. When comparing, the DVCS that has α¯¯=α $\bar{α} = α$ then, in the overall view, the clearness of the recovered secret image of the PVCS is the same as the clearness of the recovered secret image of a DVCS. However, because of the probabilistic nature, a PVCS is disadvantaged in displaying the details of the original secret image, for example, a thin line in the original secret image is likely to be displayed as a dotted line in a PVCS.

11.3 Misalignment with Integer Number of Subpixels

According to the traditional view, the subpixels of the transparencies should be aligned precisely. Here, we point out that, to recover the secret image visually, it is not necessary to align the subpixels precisely. In this section, we will only consider the misalignment with integer number of subpixels.

We will show that, by shifting one of the shares by some number (at most m − 1) of subpixels to the right (resp. left), one can still recover the secret image visually, for the reason that the average contrast α¯¯≠0 $\bar{α} \neq 0$ . This result can naturally be extended to the case when more than one share is shifted. However, we leave the numerical analysis of this case to the interested readers. So, in this section, we will only consider the case with only one share (transparency) being shifted by some number of subpixels. And we call the scheme with a share being shifted the shifted scheme, and the basis matrices and share matrices of the shifted scheme are called the shifted basis matrices and shifted share matrices.

We first give an example to show this phenomenon.

Example 1 We take the (2, 2)-DVCS as an example, where the basis matrices of the scheme are,

M 0 = [100100] a n d M 1 = [100010]

$M_{0} = [\begin{matrix} 100 \\ 100 \end{matrix}] a n d M_{1} = [\begin{matrix} 100 \\ 010 \end{matrix}]$

Images

FIGURE 11.1
The stacking results of the (2,2)-DVCS (a) when no share is shifted; (b) when one share is shifted by one subpixels; (c) when one share is shifted by two subpixel. A printed-text ”CRYPTO” is tested.

Figure 11.1 are the experimental results of the recovered secret image, where (a) is the recovered secret image without being shifted, and (b) is the recovered secret image with the second share being shifted to the left by one subpixel, and (c) is the recovered secret image with the second share being shifted to the left by 2 subpixels. From the experimental results we notice that, the original secret image can be recovered visually by shifting one or two subpixels for the (2, 2)-DVCS with pixel expansion m − 3. And the clearness of the recovered secret image with two subpixels being shifted is not as clear as the one with one subpixel being shifted. Furthermore, the shifted scheme is not a DVCS anymore; we give an example to show this point:

Example 2 Take the share matrices S0=[010010] $S^{0} = [\begin{matrix} 010 \\ 010 \end{matrix}]$ and S1=[100010] $S^{1} = [\begin{matrix} 100 \\ 010 \end{matrix}]$ as an example, which are chosen from the permutations of the basis matrices M₀ and M₁ in Example 1. By shifting the second share by one subpixel to the left, we get the following four matrices:

S 00 = [* 0 ∣ ∣ ∣ 010100] S 01 = [* 0 ∣ ∣ ∣ 010101] S 10 = [* 0 ∣ ∣ ∣ 100100] S 11 = [* 0 ∣ ∣ ∣ 100101]

$S_{0}^{0} = [\begin{matrix} * \\ 0 \end{matrix} | \begin{matrix} 010 \\ 100 \end{matrix}] S_{1}^{0} = [\begin{matrix} * \\ 0 \end{matrix} | \begin{matrix} 010 \\ 101 \end{matrix}] S_{0}^{1} = [\begin{matrix} * \\ 0 \end{matrix} | \begin{matrix} 100 \\ 100 \end{matrix}] S_{1}^{1} = [\begin{matrix} * \\ 0 \end{matrix} | \begin{matrix} 100 \\ 101 \end{matrix}]$

where Sij, i=0,1,j=0,1 $S_{j}^{i}, i = 0, 1, j = 0, 1$ , is the shifted share matrix that a subpixel j is shifted into Sⁱ. The left bottom subpixel of Sⁱ is shifted out, and the asterisk * in the Sij $S_{j}^{i}$ can be either 1 or 0, which belongs to the pixel on the left of the pixel that we considered. So, here and hereafter, we no longer consider the two subpixels anymore, i.e., we only need to consider the right 3 columns in the shifted share matrix Sij $S_{j}^{i}$ .

For the above four shifted share matrices, the stacking Hamming weights are 2, 3, 1, and 2. In particular, the stacking Hamming weight of S00 $S_{0}^{0}$ and S11 $S_{1}^{1}$ are the same. Here and hereafter, the stacking Hamming weight means the Hamming weight of the resulting vector generated by stacking the shares. Hence, the shifted scheme is not a DVCS anymore.

Generally, we aim at proving the conclusion that, the shifted scheme can visually recover the original secret image based on the (k, n)-DVCS. However, it is noticed that this proof can be reduced to the proof based on the (2, 2)-DVCS in the case that only one share is shifted. The reason is as follows:

First, a (k, n)-DVCS consists of (nk) (k,k) $(\begin{matrix} n \\ k \end{matrix}) (k, k)$ -DVCS. For a set of k shares, if no share is shifted, then the k shares can recover the secret image obviously. And because we only consider the case when only one of the n shares is shifted, we only need to consider the k shares that contain the shifted share, i.e., we only need to prove our conclusion based on a (k, k)-DVCS.

Second, denote the k shares of a (k, k)-DVCS as s₁, s₂, ⋯ ,s_k, without loss of generality, let s_k be the share that is shifted, and let s′k ${s^{'}}_{k}$ be the resulting image of stacking the remaining k − 1 shares s₁, s₂, ⋯ , s_k−i together. Then the scheme becomes a (2, 2)-DVCS, where the two shares are s′k ${s^{'}}_{k}$ and s_k. Note that, the stacking result of this (2, 2)-DVCS is the same as that of the previous (k, k)-DVCS. The previous (k, k)-DVCS can visually recover the secret image if and only if s′k ${s^{'}}_{k}$ and s_k can do so. Hence, it is sufficient to prove the conclusion based on a (2, 2)-DVCS.

We analyze the structure of the basis matrix of the (2, 2)-DVCS. Denote M₀ and M₁ as the basis matrices of the (2, 2)-DVCS, then the M₀ and M₁, without loss of generality, are in the following form:

M 0 = ⎡ ⎣ ⎢ 1 \dots 10 \dots 01 \dots 10 \dots 0 1 \dots 1      a 0 \dots 0      b 0 \dots 0      c 1 \dots 1      d ⎤ ⎦ ⎥,

$M_{0} = [\begin{matrix} 1 \dots 10 \dots 01 \dots 10 \dots 0 \\ \underset{a}{\underset{︸}{1 \dots 1}} \underset{b}{\underset{︸}{0 \dots 0}} \underset{c}{\underset{︸}{0 \dots 0}} \underset{d}{\underset{︸}{1 \dots 1}} \end{matrix}],$

and

M 1 = ⎡ ⎣ ⎢ 1 \dots 10 \dots 01 \dots 10 \dots 0 1 \dots 1      a' 0 \dots 0      b' 0 \dots 0      c' 1 \dots 1      d' ⎤ ⎦ ⎥,

$M_{1} = [\begin{matrix} 1 \dots 10 \dots 01 \dots 10 \dots 0 \\ \underset{a^{'}}{\underset{︸}{1 \dots 1}} \underset{b^{'}}{\underset{︸}{0 \dots 0}} \underset{c^{'}}{\underset{︸}{0 \dots 0}} \underset{d^{'}}{\underset{︸}{1 \dots 1}} \end{matrix}],$

where a, b, c, d, a′, b′, c′, and d′ are nonnegative integers satisfying a+c+d = l and a′ + c′ + d′ = h. According to the contrast and security property of Definition 1, we have,

⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ a + b + c + d = a' + b' + c' + d' a + c = a' + c' a + d = a' + d' b > b'

${\begin{array}{l} a + b + c + d = a^{'} + b^{'} + c^{'} + d^{'} \\ a + c = a^{'} + c^{'} \\ a + d = a^{'} + d^{'} \\ b > b^{'} \end{array}$

solving the above equations, we get a − a' = b − b' = c' − c = d′ − d. Let e = b − b', hence, by deleting identical columns of M₀ and M₁, we get,

M' 0 = ⎡ ⎣ ⎢ 1 \dots 10 \dots 0 1 \dots 1      e 0 \dots 0      e ⎤ ⎦ ⎥

${M^{'}}_{0} = [\begin{matrix} 1 \dots 10 \dots 0 \\ \underset{e}{\underset{︸}{1 \dots 1}} \underset{e}{\underset{︸}{0 \dots 0}} \end{matrix}]$

and,

M' 1 = ⎡ ⎣ ⎢ 1 \dots 10 \dots 0 0 \dots 0      e 1 \dots 1      e ⎤ ⎦ ⎥

${M^{'}}_{1} = [\begin{matrix} 1 \dots 10 \dots 0 \\ \underset{e}{\underset{︸}{0 \dots 0}} \underset{e}{\underset{︸}{1 \dots 1}} \end{matrix}]$

where the number of columns in M′0 ${M^{'}}_{0}$ and M′1 ${M^{'}}_{1}$ is 2e.

Now we know that the basis matrices of an arbitrary (2, 2)-DVCS M₀ and M₁ contain the same number of identical columns [11],[10],[01] $\begin{matrix} [\begin{matrix} 1 \\ 1 \end{matrix}], & [\begin{matrix} 1 \\ 0 \end{matrix}], & [\begin{matrix} 0 \\ 1 \end{matrix}] \end{matrix}$ , and [00] $[\begin{matrix} 0 \\ 0 \end{matrix}]$ apart from the submatrices M′0 ${M^{'}}_{0}$ and M′1 ${M^{'}}_{1}$ . Hence, without loss of generality, they can be represented as the following form:

M 0 = ⎡ ⎣ ⎢ 1 \dots 10 \dots 01 \dots 10 \dots 01 \dots 10 \dots 0 1 \dots 1      a' 0 \dots 0      b' 0 \dots 0      c' 1 \dots 1      d 1 \dots 1      e 0 \dots 0      e ⎤ ⎦ ⎥

$M_{0} = [\begin{matrix} 1 \dots 10 \dots 01 \dots 10 \dots 01 \dots 10 \dots 0 \\ \underset{a^{'}}{\underset{︸}{1 \dots 1}} \underset{b^{'}}{\underset{︸}{0 \dots 0}} \underset{c^{'}}{\underset{︸}{0 \dots 0}} \underset{d}{\underset{︸}{1 \dots 1}} \underset{e}{\underset{︸}{1 \dots 1}} \underset{e}{\underset{︸}{0 \dots 0}} \end{matrix}]$

and

M 1 = ⎡ ⎣ ⎢ 1 \dots 10 \dots 01 \dots 10 \dots 01 \dots 10 \dots 0 1 \dots 1      a' 0 \dots 0      b' 0 \dots 0      c 1 \dots 1      d 0 \dots 0      e 1 \dots 1      e ⎤ ⎦ ⎥ .

$M_{1} = [\begin{matrix} 1 \dots 10 \dots 01 \dots 10 \dots 01 \dots 10 \dots 0 \\ \underset{a^{'}}{\underset{︸}{1 \dots 1}} \underset{b^{'}}{\underset{︸}{0 \dots 0}} \underset{c}{\underset{︸}{0 \dots 0}} \underset{d}{\underset{︸}{1 \dots 1}} \underset{e}{\underset{︸}{0 \dots 0}} \underset{e}{\underset{︸}{1 \dots 1}} \end{matrix}] .$

Let m be the pixel expansion, then it is obvious that m = a' + b' + c + d + 2e. The collections C₀ and C₁ contain all the permutations of the basis matrices M₀ and M₁ , and hence each has m! share matrices.

The shifted scheme is generated as follows:

Shift the second row of the m! share matrices in C₀ (resp. C₁) to the left (resp. right) by r subpixels, and let c₁,c₂, ⋯ ,c_r be the r-bit string that is shifted in, where each c_i ∈ {0,1} represents a subpixel. By the above discussion, we get m! shifted share matrices for C₀ (resp. C₁). Take the share matrix M₀ ∈ C₀ as an example, then the shifted share matrix, denoted by M(r)0 $M_{0}^{(r)}$ , is as follows:

M (r) 0 = ⎡ ⎣ ⎢ * \dots * 1 \dots 10 \dots 01 \dots 10 \dots 01 \dots 10 \dots 0 1 \dots 1      a' 0 \dots 0      b' 0 \dots 0      c 1 \dots 1      d 1 \dots 1      e 0 \dots 0      e c 1 \dots c r        r ⎤ ⎦ ⎥,

$M_{0}^{(r)} = [\begin{matrix} * \dots * 1 \dots 10 \dots 01 \dots 10 \dots 01 \dots 10 \dots 0 \\ \underset{a^{'}}{\underset{︸}{1 \dots 1}} \underset{b^{'}}{\underset{︸}{0 \dots 0}} \underset{c}{\underset{︸}{0 \dots 0}} \underset{d}{\underset{︸}{1 \dots 1}} \underset{e}{\underset{︸}{1 \dots 1}} \underset{e}{\underset{︸}{0 \dots 0}} \underset{r}{\underset{︸}{c_{1} \dots c_{r}}} \end{matrix}],$

where c₁ ⋯ c_r of share 2 are the adjacent subpixels of the right pixel that are shifted in.

By going through all m! share matrices of C₀ and C₁ and all the possible string of subpixels c₁ ⋯ c_r ∈ {0,1}^r, where {0,1}^r is the set of all the binary strings of length r, the shifted scheme is generated. Hence, we have:

Theorem 1 The shifted scheme of a DVCS is a PVCS, where the average contrast of the shifted scheme is α¯¯=−(m−r)em2(m−1) $\bar{α} = - \frac{(m - r) e}{m^{2} (m - 1)}$ , where 1≤ r ≤ m − 1 is the number of subpixels by which the share 2 (the second share) is shifted.

Proof: Without loss of generality, we only prove the case when the share 2 is shifted to the left, which is equivalent to the case when the share 1 (the first share) is shifted to the right. Note that, swapping rows 1 and 2 corresponds to swapping the parameters c and d. We observe that, since the share matrices of the DVCS satisfy condition 3 of Definition 1 and the shifting operation is the same for matrices in C₀ and C₁, the share matrices of the shifted scheme satisfy condition 3 of Definition 2.

First, we prove the case that the share 2 is shifted by one subpixel, and then we extend it to the case when it is shifted by r subpixels.

When share 2 is shifted by one subpixel, the adjacent right subpixel of share 2 is shifted in. Let p₁ be the probability that a 1 is shifted in, and p₀ be the probability that a 0 is shifted in. Because the share matrices are all the permutations of the basis matrices, so p₁ and p₀ have fixed values and p₁ + p₀ = 1, i.e., the shifted in subpixel is either 1 or 0. More precisely, by the above discussion we have p1=a′+d+em $p_{1} = \frac{a^{'} + d + e}{m}$ and p0=b′+c+em $p_{0} = \frac{b^{'} + c + e}{m}$ . In the general case when r subpixels are shifted in, denote p_c as the probability that a string of subpixels c is shifted in, we also have ∑c∈{0,1}rpc=1 $\sum_{c \in {0, 1}^{r}} p_{c} = 1$ .

Because, under the OR operation, the stacking of two black subpixels results in a black subpixel, i.e., 1 OR 1 = 1, so this means that there is a black subpixel that is ineffective (overlapped). Now we define a black pixel (value 1) to be ineffective if it does not contribute to the total number of black pixels in the recovered secret image. There are three cases when a black subpixel 1 is ineffective: (1) when that is in the top right corner of the matrix M₀ (or M₁) and another 1 is shifted in, this results in a overlap; (2) when that is in the bottom left corner of the matrix which is then shifted out (appear below an asterisk ‘*’); and (3) when an overlap happens after a shift, which is possible on the first m − 1 positions (and m − r positions in general). Hence, the total Hamming weight of the stacking of the shifted share matrices can be calculated by the total number of the 1’s subtracted by the number of the 1’s that are ineffective (when two 1’s overlapped, we only count one as ineffective).

In the first case, denote by s10,c $s_{0, c}^{1}$ and s11,c $s_{1, c}^{1}$ the number of 1’s that are ineffective for the collections C₀ and C₁, respectively when the subpixel c is shifted in. Since there are m! share matrices in the collection C₀ and C₁, so the total number of 1’s that are ineffective in the top right corner of all the share matrices in C₀ and C₁ is s10,1=s11,1=a′+c+emm $s_{0, 1}^{1} = s_{1, 1}^{1} = \frac{a^{'} + c + e}{m} m$ ! (when a 1 is shifted in) and s0 s10,0=s11,0=0 $s_{0, 0}^{1} = s_{1, 0}^{1} = 0$ (when a 0 is shifted in), where a′+c+em $\frac{a^{'} + c + e}{m}$ is the probability of the 1’s in the top right corner of the first row.

In the second case, denote by s20,c $s_{0, c}^{2}$ and s21,c $s_{1, c}^{2}$ the number of 1’s that are ineffective for the collections C₀ and C₁, respectively when the subpixel c is shifted in. So the total number of 1’s that are ineffective in the bottom left corner of all the share matrices in C₀ and C is s21,1=s20,1=s21,0=s20,0=a′+d+emm! $s_{1, 1}^{2} = s_{0, 1}^{2} = s_{1, 0}^{2} = s_{0, 0}^{2} = \frac{a^{'} + d + e}{m} m!$ , where a′+d+em $\frac{a^{'} + d + e}{m}$ is the probability of the 1’s in the bottom left corner of the second row.

In the third case, denote by s30,c $s_{0, c}^{3}$ and s31,c $s_{1, c}^{3}$ the number of 1’s that are ineffective for the collections C₀ and C₁ respectively when the subpixel c is shifted in. Note that, the pattern [11] $[\begin{matrix} 1 \\ 1 \end{matrix}]$ in the shifted share matrices is the shifted result of the following four patterns, [1101],[1011],[1001] $[\begin{matrix} 11 \\ 01 \end{matrix}], [\begin{matrix} 10 \\ 11 \end{matrix}], [\begin{matrix} 10 \\ 01 \end{matrix}]$ , and [1111] $[\begin{matrix} 11 \\ 11 \end{matrix}]$ in the collections C₀ and C₁. We calculate the probability of the first pattern [1101] $[\begin{matrix} 11 \\ 01 \end{matrix}]$ for example, and the other three patterns can be calculated similarly. The probability that the pattern [10] $[\begin{matrix} 1 \\ 0 \end{matrix}]$ appears at the column i in the matrices of the collection C₁ is c+em $\frac{c + e}{m}$ , and, fixing this pattern, the probability that the pattern [11] $[\begin{matrix} 1 \\ 1 \end{matrix}]$ appears at the column i + 1 of the collection C₁ is a′m−1 $\frac{a^{'}}{m - 1}$ , where 1 ≤ i ≤ m − 1. So the probability that the pattern [1101] $[\begin{matrix} 11 \\ 01 \end{matrix}]$ appears both at the columns i and i + 1 in the collection C₁ is c+ema′m−1 $\frac{c + e}{m} \frac{a^{'}}{m - 1}$ . Similarly, for the remaining three patterns, the results are shown in Table 11.2.

Table 11.2 The probability of the four patterns appearing at the columns i and i + 1 in the collections C₀ and C₁.

collectionspatterns	[1011] $[\begin{matrix} 10 \\ 11 \end{matrix}]$	[1111] $[\begin{matrix} 11 \\ 11 \end{matrix}]$	[1001] $[\begin{matrix} 10 \\ 01 \end{matrix}]$	[1101] $[\begin{matrix} 11 \\ 01 \end{matrix}]$
C₁	a′md+em−1 $\frac{a^{'}}{m} \frac{d + e}{m - 1}$	a′ma′−1m−1 $\frac{a^{'}}{m} \frac{a^{'} - 1}{m - 1}$	c+emd+em−1 $\frac{c + e}{m} \frac{d + e}{m - 1}$	c+ema′m−1 $\frac{c + e}{m} \frac{a^{'}}{m - 1}$
C₀	a′+emdm−1 $\frac{a^{'} + e}{m} \frac{d}{m - 1}$	a′+ema′+e−1m−1 $\frac{a^{'} + e}{m} \frac{a^{'} + e - 1}{m - 1}$	cmdm−1 $\frac{c}{m} \frac{d}{m - 1}$	cma′+em−1 $\frac{c}{m} \frac{a^{'} + e}{m - 1}$

The collection C₀ and C₁ contain all the column permutations of the basis matrices in all possible ways, and there are only m − 1 choices for the value of i, so the total number of 1’s that are ineffective of the four patterns of the collection C₁ is S31,1=S31,0=(a′md+em−1+a′ma′−1m−1+c+emd+em−1+c+ema′m−1)(m−1)m! $S_{1, 1}^{3} = S_{1, 0}^{3} = (\frac{a^{'}}{m} \frac{d + e}{m - 1} + \frac{a^{'}}{m} \frac{a^{'} - 1}{m - 1} + \frac{c + e}{m} \frac{d + e}{m - 1} + \frac{c + e}{m} \frac{a^{'}}{m - 1}) (m - 1) m!$ , and that of the collection C₀ is S30,1=S30,0=(a′+emdm−1+a′+ema′+e−1m−1+cmdm−1+cma′+em−1)(m−1)m! $S_{0, 1}^{3} = S_{0, 0}^{3} = (\frac{a^{'} + e}{m} \frac{d}{m - 1} + \frac{a^{'} + e}{m} \frac{a^{'} + e - 1}{m - 1} + \frac{c}{m} \frac{d}{m - 1} + \frac{c}{m} \frac{a^{'} + e}{m - 1}) (m - 1) m!$ .

Denote the total number of 1’s in the share matrices in collections C₀ and C₁ plus the number of 1’s in the subpixel c that is shifted in as T_{0, c} and T_{1, c}, respectively. Then, when a 1 is shifted in, we have T_0,1 = T_{1, 1} = (2a' + c + d + 2e + 1)m!, and when a 0 is shifted in, we have T_0,0 = T_{1, 0} = (2a' + c+d+2e)m!.

Denote T_{c, C} as the total stacking Hamming weight of all the matrices of the collection C (C₀ or C₁) when a string of subpixels c are shifted in. The above discussion shows that when a 1 is shifted in, the total stacking Hamming weight of all the matrices of the collection C₁ is

T 1, C 1 = T 1, 1 - s 1 1, 1 - s 2 1, 1 - s 3 1, 1 = [(2 a' + c + d + 2 e + 1) - a ' + d + e m - a ' + c + e m - (a ' ( d + e ) m + a ' ( a ' - 1 ) m + ( c + e ) ( d + e ) m + ( c + e ) a ' m)] m!

$\begin{array}{l} T_{1, C_{1}} = T_{1, 1} - s_{1, 1}^{1} - s_{1, 1}^{2} - s_{1, 1}^{3} \\ = [(2 a^{'} + c + d + 2 e + 1) - \frac{a^{'} + d + e}{m} - \frac{a^{'} + c + e}{m} \\ - (\frac{a^{'} (d + e)}{m} + \frac{a^{'} (a^{'} - 1)}{m} + \frac{(c + e) (d + e)}{m} + \frac{(c + e) a^{'}}{m})] m! \end{array}$

and that of the collection C₀ is

T 1, C 0 = T 0, 1 - s 1 0, 1 - s 2 0, 1 - s 3 0, 1 = [(2 a' + c + d + 2 e + 1) - a ' + d + e m - a ' + c + e m - (( a ' + e ) d m + ( a ' + e ) ( a ' + e - 1 ) ) m + c d m + c ( a ' + e ) m)] m!

$\begin{array}{l} T_{1, C_{0}} = T_{0, 1} - s_{0, 1}^{1} - s_{0, 1}^{2} - s_{0, 1}^{3} \\ = [(2 a^{'} + c + d + 2 e + 1) - \frac{a^{'} + d + e}{m} - \frac{a^{'} + c + e}{m} \\ - (\frac{(a^{'} + e) d}{m} + \frac{(a^{'} + e) (a^{'} + e - 1))}{m} + \frac{c d}{m} + \frac{c (a^{'} + e)}{m})] m! \end{array}$

When a 0 is shifted in, the total stacking Hamming weight of the collection C₁ is,

T 0, C 0 = T 1, 0 - s 1 1, 0 - s 2 1, 0 - s 3 1, 0 = [(2 a' + c + d + 2 e) - a ' + d + e m - (a ' ( d + e ) m + a ' ( a ' - 1 ) m + ( c + e ) ( d + e ) m + ( c + e ) a ' m)] m!

$\begin{array}{l} T_{0, C_{0}} = T_{1, 0} - s_{1, 0}^{1} - s_{1, 0}^{2} - s_{1, 0}^{3} \\ = [(2 a^{'} + c + d + 2 e) - \frac{a^{'} + d + e}{m} - \\ (\frac{a^{'} (d + e)}{m} + \frac{a^{'} (a^{'} - 1)}{m} + \frac{(c + e) (d + e)}{m} + \frac{(c + e) a^{'}}{m})] m! \end{array}$

and that of the collection C₀ is

T 0, C 0 = T 0, 0 - s 1 0, 0 - s 2 0, 0 - s 3 0, 0 = [(2 a' + c + d + 2 e) - a ' + d + e m - (( a ' + e ) d m + ( a ' + e ) ( a ' + e - 1 ) m + c d m + c ( a ' + e ) m)] m!

$\begin{array}{l} T_{0, C_{0}} = T_{0, 0} - s_{0, 0}^{1} - s_{0, 0}^{2} - s_{0, 0}^{3} \\ = [(2 a^{'} + c + d + 2 e) - \frac{a^{'} + d + e}{m} - \\ (\frac{(a^{'} + e) d}{m} + \frac{(a^{'} + e) (a^{'} + e - 1)}{m} + \frac{c d}{m} + \frac{c (a^{'} + e)}{m})] m! \end{array}$

We now define the average stacking Hamming weight of each share matrix to be the total stacking Hamming weight of all the share matrices being divided by the number of the share matrices, i.e., Tc,Cm! $\frac{T_{c, C}}{m!}$ . Then the difference between the average stacking Hamming weight of each share matrix of the shifted collections C₀ and C₁, denoted by D_A, is

D A = (T 1, C 1 - T 1, C 0) p 1 + (T 0, C 1 - T 0, C 0) p 0 = - e ( p 1 + p 0 ) m = - e m

$D_{A} = (T_{1, C_{1}} - T_{1, C_{0}}) p_{1} + (T_{0, C_{1}} - T_{0, C_{0}}) p_{0} = - \frac{e (p_{1} + p_{0})}{m} = - \frac{e}{m}$

According to the definition of the average contrast in Section 11.2, with h¯=T1,C1p1+T0,C1p0 $\bar{h} = T_{1, C_{1} p_{1}} + T_{0, C_{1} p_{0}}$ and l¯=T1,C0p1+T0,C0p0 $\bar{l} = T_{1, C_{0} p_{1}} + T_{0, C_{0} p_{0}}$ , we get the value of the average contrast α¯¯=h¯−l¯m=DAm=−em2 $\bar{α} = \frac{\bar{h} - \bar{l}}{m} = \frac{D_{A}}{m} = - \frac{e}{m^{2}}$ .

Now we consider the general case when the share 2 is shifted by r subpixels. For this case there are 2^r possible subpixels that can be shifted in. For example, for r = 2, the shifted in strings of subpixels have four cases, 00, 01, 10 and 11. Denote by p₀₀, p₀₁ p₁₀ and p₁₁ the probabilities of these four cases to happen respectively, then we have p₀₀ + p₀₁ + p₁₀ + p₁₁ = 1.

We consider the string of subpixels c, let the Hamming weight of c be s, i.e., w(c) = s. The total number of 1’s that are ineffective in the top right corner of all the share matrices in C₀ and C₁ is s10,c=s11,c=s ⋅a′+c+emm! $s_{0, c}^{1} = s_{1, c}^{1} = s \cdot \frac{a^{'} + c + e}{m} m!$ , and the total number of 1’s that are ineffective in the bottom left corner of all the share matrices in C₀ and C₁ is s20,c=s21,c=r ⋅a′+d+emm! $s_{0, c}^{2} = s_{1, c}^{2} = r \cdot \frac{a^{'} + d + e}{m} m!$ . For the third case, the pattern [11] $[\begin{matrix} 1 \\ 1 \end{matrix}]$ in the shifted share matrices is the shifted result of the following four patterns, ⎡⎣⎢⎢⎢1⋯1r0⋯1r⎤⎦⎥⎥⎥,⎡⎣⎢⎢⎢1⋯0r1⋯1r⎤⎦⎥⎥⎥,⎡⎣⎢⎢⎢1⋯0r0⋯1r⎤⎦⎥⎥⎥ $[\begin{matrix} 1 \underset{r}{\underset{︸}{\dots 1}} \\ 0 \underset{r}{\underset{︸}{\dots 1}} \end{matrix}], [\begin{matrix} 1 \underset{r}{\underset{︸}{\dots 0}} \\ 1 \underset{r}{\underset{︸}{\dots 1}} \end{matrix}], [\begin{matrix} 1 \underset{r}{\underset{︸}{\dots 0}} \\ 0 \underset{r}{\underset{︸}{\dots 1}} \end{matrix}]$ and ⎡⎣⎢⎢⎢1⋯1r1⋯1r⎤⎦⎥⎥⎥ $[\begin{matrix} 1 \underset{r}{\underset{︸}{\dots 1}} \\ 1 \underset{r}{\underset{︸}{\dots 1}} \end{matrix}]$ in the collections C₀ and C₁ , and there are only m − r choices for the value of the position i, so the total number of the 1’s that are ineffective of the four patterns of the collection C₁ is

(a ' m d + e m - 1 + a ' m a ' - 1 m - 1 + c + e m d + e m - 1 + c + e m a ' m - 1) (m - r) m!

$(\frac{a^{'}}{m} \frac{d + e}{m - 1} + \frac{a^{'}}{m} \frac{a^{'} - 1}{m - 1} + \frac{c + e}{m} \frac{d + e}{m - 1} + \frac{c + e}{m} \frac{a^{'}}{m - 1}) (m - r) m!$

and of the collection C₀ is

(a ' + e m d m - 1 + a ' + e m a ' + e - 1 m - 1 + c m d m - 1 + c m a ' + e m - 1) (m - r) m!

$(\frac{a^{'} + e}{m} \frac{d}{m - 1} + \frac{a^{'} + e}{m} \frac{a^{'} + e - 1}{m - 1} + \frac{c}{m} \frac{d}{m - 1} + \frac{c}{m} \frac{a^{'} + e}{m - 1}) (m - r) m!$

Hence, when a string of subpixels of c is shifted in, the total stacking Hamming weight of all the matrices of the collection C₁ is

T c, C 1 = [(2 a' + c + d + 2 e + s) - r \cdot a ' + d + e m - s \cdot a ' + c + e m - (a ' ( d + e ) m + a ' ( a ' - 1 ) m + ( c + e ) ( d + e ) m + ( c + e ) a ' m) m - r m - 1] m!

$\begin{array}{l} T_{c, C_{1}} = [(2 a^{'} + c + d + 2 e + s) - r \cdot \frac{a^{'} + d + e}{m} - s \cdot \frac{a^{'} + c + e}{m} \\ - (\frac{a^{'} (d + e)}{m} + \frac{a^{'} (a^{'} - 1)}{m} + \frac{(c + e) (d + e)}{m} + \frac{(c + e) a^{'}}{m}) \frac{m - r}{m - 1}] m! \end{array}$

and that of the collection C₀ is

T c, C 0 = [(2 a' + c + d + 2 e + s) - r \cdot a ' + d + e m - s \cdot a ' + c + e m - (( a ' + e ) d m + ( a ' + e ) ( a ' + e - 1 ) ) m + c d m + c ( a ' + e ) m) m - r m - 1] m! .

$\begin{array}{l} T_{c, C_{0}} = [(2 a^{'} + c + d + 2 e + s) - r \cdot \frac{a^{'} + d + e}{m} - s \cdot \frac{a^{'} + c + e}{m} \\ - (\frac{(a^{'} + e) d}{m} + \frac{(a^{'} + e) (a^{'} + e - 1))}{m} + \frac{c d}{m} + \frac{c (a^{'} + e)}{m}) \frac{m - r}{m - 1}] m! . \end{array}$

Hence, the difference between the average stacking Hamming weight of each share matrix of the shifted collections C₀ and C₁, denoted by D_A, is

D A = (T 1 \dots 1, C 1 - T 1 \dots 1, C 0) p 1 \dots 1 + \dots + (T 0 \dots 0, C 1 - T 0 \dots 0, C 0) p 0 \dots 0 = - e ( p 1 \dots 1 + \dots + p 0 \dots 0 ) m m - r m - 1 = - e m m - r m - 1

$\begin{array}{l} D_{A} = (T_{1 \dots 1, C_{1}} - T_{1 \dots 1, C_{0}}) p_{1 \dots 1} + \dots + (T_{0 \dots 0, C_{1}} - T_{0 \dots 0, C_{0}}) p_{0 \dots 0} \\ = - \frac{e (p_{1 \dots 1} + \dots + p_{0 \dots 0})}{m} \frac{m - r}{m - 1} \\ = - \frac{e}{m} \frac{m - r}{m - 1} \end{array}$

and the average contrast is

α ¯ ¯ = D A m = - e m 2 m - r m - 1 .

$\bar{α} = \frac{D_{A}}{m} = - \frac{e}{m^{2}} \frac{m - r}{m - 1} .$

Because the shifted scheme is not a DVCS anymore and α¯¯ ≠ 0, let h¯=T1⋯1,C1p1⋯1+⋯+T0⋯0,C1p0⋯0 $\bar{α} \neq 0, let \bar{h} = T_{1 \dots 1, C_{1} p 1 \dots 1} + \dots + T_{0 \dots 0, C_{1} p 0 \dots 0}$ and l¯ = T1⋯1,C0p1⋯1+⋯+T0⋯0,C0p0⋯0 $\bar{l} = T_{1 \dots 1, C_{0} p 1 \dots 1} + \dots + T_{0 \dots 0, C_{0} p 0 \dots 0} $ , then it is known that the shifted scheme is a PVCS. This completes the proof of Theorem 1. □

Note that, after a shift, the value of the average contrast has a negative value α¯¯ < 0 $\bar{α} < 0$ , which means that the recovered secret image is the complementary image of the original one, and the absolute value of α¯¯ $\bar{α}$ reflects how clear the image can be viewed visually.

The above Theorem 1 shows that, to align the transparencies when decrypting the DVCS, one does not need to align the transparencies precisely. So, when the participants of a DVCS want to align the transparencies, for example, the transparencies in Example 1, they can first align the transparencies precisely in the vertical direction, and then move the second transparencies to the right then to the left in the horizontal direction. Then they will get the recovered secret image for three times. Furthermore, this phenomenon also helps to determine the size of the subpixels printed on the transparencies.

For other visual cryptography schemes, such as the extended visual cryptography schemes in [2], the visual cryptography schemes for the general access structures [1] and the color visual cryptography schemes [15, 12], they all have the phenomenon stated above. The proof for these visual cryptography schemes can be modified from that of Theorem 1.

11.4 Misalignment with Less Than One Subpixel

In this section, we do further investigation on misalignment with less than one subpixel. We show that the secret image can still be recovered visually by a slight misalignment. We first give an example, a (2, 2)-VCS, to show this phenomenon. Denote (d_x, d_y) as the horizontal and vertical misalignment deviations from the original position of the subpixel.

Example 3 The images (a), (b), and (c) in Figure 11.2 show the recovered secret image of a (2,2)-VCS for three misalignment deviations, (d_x,d_y) = (0, 0), (0.5, 0), and (1, 2) (unit: subpixel).

Images

FIGURE 11.2
Recovered secret images of a (2,2)-VCS for three misalignment deviations (a) (d_x,d_y) = (0,0), (b) (d_x,d_y) = (0.5,0), and (c) (d_x,d_y) = (1, 2).

From Figure 11.2, we can observe that, the clearness ofFigure 11.2 (b) is worse than the Figure 11.2 (a), and the secret on Figure 11.2 (c) is completely invisible.

Figure 11.2 shows the case that only two shares are superimposed. The misalignment problem will become more complex for stacking k shares for a ( k, n)-VCS. Note that, the recovered image will disappear if any one out of k shares is not at the correct position. In fact the misalignment problem critically increases as k grows.

The next two subsections are organized as follows: first, we will investigate the conditions that the secret image can still be observed when the shares are slightly misaligned, whereby saying slight misalignment we mean deviation (d_x, d_y) satisfying 0 ≤ d_x, d_y ≤ 1; and then we will investigate the misalignment tolerance of large and small pixels. To simplify the discussion, we only consider the case of (2, 2)-VCS.

11.4.1 Shares with Slightly Misalignment Can Still Recover the Secret Image

We consider a (2, 2)-VCS with deviation (d_x, d_y), where a pixel 1W1B (resp. 1B1W) represents a white pixel that contains a white (resp. black) and a black (resp. white) subpixel; and a pixel 2B0W represents a black pixel that contains two black subpixels. All possible four cases, (a1), ( a2), (b1), and (b2), of stacked shares with deviation (d_x, d_y) are shown in Figure 11.3. The stacked results in Figure 11.3 are marked with red boxes. As shown in Figure 11.3, the stacked result is divided into eight parts. Denote A₁, A₂, A₃, A₄, A′₁, A′₂, A′₃ and A′₄ as the areas of the eight parts respectively, and they satisfy the following equations.

A 1 = A' 1 = d x d y A 2 = A' 2 = (s - d x) d y A 3 = A' 3 = d x (s - d y) A 4 = A' 4 = (s - d x) (s - d y) A 1 + A 2 + A 3 + A 4 = s 2 (11.1)

$\begin{array}{l} A_{1} = {A^{'}}_{1} = d_{x} d_{y} \\ A_{2} = {A^{'}}_{2} = (s - d_{x}) d_{y} \\ A_{3} = {A^{'}}_{3} = d_{x} (s - d_{y}) \\ A_{4} = {A^{'}}_{4} = (s - d_{x}) (s - d_{y}) \\ A_{1} + A_{2} + A_{3} + A_{4} = s^{2} \end{array} (11.1)$

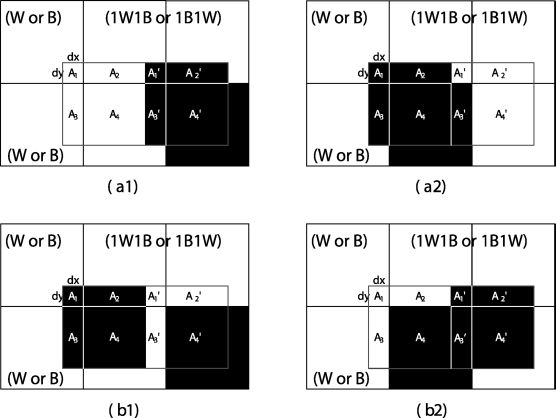
Images

FIGURE 11.3
Stacked results of white pixels (a1: 1W1B+H1W1B, a2: 1B1W+ 1B1W) and black pixels (b1: 1W1B+1B1W, b2: 1B1W+1W1B) for the same deviation ^{( d}_x, ^d_y⁾.

Denote s × s as the size of a subpixel, and denote A_{C, C} as the area in the stacked results with color C ∈ {W, B} for case c ∈ (a1), (a2), (b1), and (b2). Note that, some areas are not deterministic in Figure 11.3, for example the area A₁ in Figure 11.3 (a1) belongs to the adjacent pixel on the top left. It can be either black or white with equal probability 50%. We introduce a symbol P(A) to denote it, i.e., P(A) is the area of A to be either black or white with equal probability 50%. Furthermore, we denote P(A₁,A₂) as the area that is either A₁ or A₂ with equal probability 50% since there exist such cases that one of two areas is black and the other is white, for example the areas A′₁ or A′₂ in Figure 11.3 (a2). The symbols P(A) and P(A₁, A₂) satisfy the following equations:

min {P (A)} = 0 max {P (A)} = A P ¯ ¯ ¯ (A) = A / 2 min {P (A 1, A 2)} = min {A 1, A 2} max {P (A 1, A 2)} = max {A 1, A 2} P ¯ ¯ ¯ (A 1, A 2) = A 1 / 2 + A 2 / 2 (11.2)

$\begin{array}{l} \min {P (A)} = 0 \\ \max {P (A)} = A \\ \bar{P} (A) = A / 2 \\ \min {P (A_{1}, A_{2})} = \min {A_{1}, A_{2}} \\ \max {P (A_{1}, A_{2})} = \max {A_{1}, A_{2}} \\ \bar{P} (A_{1}, A_{2}) = A_{1} / 2 + A_{2} / 2 \end{array} (11.2)$

According to Figure 11.3, it is easy to verify the following equations:

A W, a 1 = P (A 1) + P (A 2) + P (A 3) + A 4 A B, a 1 = P (A 1) + P (A 2) + P (A 3) + A' 1 + A' 2 + A' 3 + A' 4 A W, a 2 = P (A' 1, A' 2) + A' 4 A B, a 2 = A 1 + A 2 + A 3 + A 4 + P (A' 1, A' 2) + A' 3 A W, b 1 = P (A' 1 + A' 2) + A' 3 A B, b 1 = A 1 + A 2 + A 3 + A 4 + P (A' 1 + A' 2) + A' 4 A W, b 2 = P (A 1) + P (A 2) + P (A 3) A B, b 2 = P (A 1) + P (A 2) + P (A 3) + A 4 + A' 1 + A' 2 + A' 3 + A' 4 (11.3)

$\begin{array}{l} A_{W, a 1} = P (A_{1}) + P (A_{2}) + P (A_{3}) + A_{4} \\ A_{B, a 1} = P (A_{1}) + P (A_{2}) + P (A_{3}) + {A^{'}}_{1} + {A^{'}}_{2} + {A^{'}}_{3} + {A^{'}}_{4} \\ A_{W, a 2} = P ({A^{'}}_{1}, {A^{'}}_{2}) + {A^{'}}_{4} \\ A_{B, a 2} = A_{1} + A_{2} + A_{3} + A_{4} + P ({A^{'}}_{1}, {A^{'}}_{2}) + {A^{'}}_{3} \\ A_{W, b 1} = P ({A^{'}}_{1} + {A^{'}}_{2}) + {A^{'}}_{3} \\ A_{B, b 1} = A_{1} + A_{2} + A_{3} + A_{4} + P ({A^{'}}_{1} + {A^{'}}_{2}) + {A^{'}}_{4} \\ A_{W, b 2} = P (A_{1}) + P (A_{2}) + P (A_{3}) \\ A_{B, b 2} = P (A_{1}) + P (A_{2}) + P (A_{3}) + A_{4} + {A^{'}}_{1} + {A^{'}}_{2} + {A^{'}}_{3} + {A^{'}}_{4} \end{array} (11.3)$

The following Theorem 2 shows that the stacked shares with slight misalignment can still recover the secret image. Note that, by saying the secret image is recovered by its original color, we mean that a black (resp. white) pixel in the secret image is represented by a black (resp. white) pixel in the recovered secret image; and by saying the secret image is recovered by its complementary color, we mean that a black (resp. white) pixel in the secret image is represented by a white (resp. black) pixel in the recovered secret image. In order to consist with Definition 1 and Definition 2, we generalize the definition of contrast α and average contrast α¯¯ $\bar{α}$ as follows:

α = h - l 2 s 2 a n d α ¯ ¯ = h ¯ - l ¯ 2 s 2 (11.4)

$α = \frac{h - l}{2 s^{2}} a n d \bar{α} = \frac{\bar{h} - \bar{l}}{2 s^{2}} (11.4)$

where 2s² is the area of a pixel (including two subpixels) and the definitions of h, l, h¯ $\bar{h}$ , and l¯ $\bar{l}$ are the same as that in Definition 1 and Definition 2.

Theorem 2 For a misaligned (2, 2)-VCS, denote (d_x,d_y) as the deviation of the stacked shares, then the secret image can still be recovered if(d_x, d_y) falls in the regions of R₁, R₂, and R₃ in Figure 11.4, where the properties of the misaligned scheme are shown in Table 11.3.

Proof: Denote lWblack area (resp. hBblack area) $l_{b l a c k a r e a}^{W} (resp . h_{b l a c k a r e a}^{B})$ as the maximum (resp. minimum) black area of a white (resp. black) pixel, denote l¯Wblack area (resp. h¯Bblack area) ${\bar{l}}_{b l a c k a r e a}^{W} (resp . {\bar{h}}_{b l a c k a r e a}^{B})$ as the average black area of a white (resp. black) pixel, denote hBwhite area $h_{w h i t e a r e a}^{B}$ (resp. lWwhite area $l_{w h i t e a r e a}^{W}$ ) as the minimum (resp. maximum) white area of a black (resp. white) pixe1, denote h¯Bwhite area(resp. l¯Wwhite area) ${\bar{h}}_{w h i t e a r e a}^{B} (resp . {\bar{l}}_{w h i t e a r e a}^{W})$ as the average white area of a black (resp. white) pixel. According to Figure 11.3, we have:

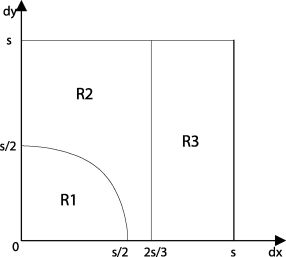
Images

FIGURE 313.11
The regions of deviation ( d_x, d_y) that can recover the secret image.

Table 11.3 The properties of the misaligned schemes.

regions	R₁	R₂	R₃
(d_x, d_y) satisfy	(s − d_x)(s − d_y) > s²/2 0 ≤ d_x,d_y < s	0 ≤ d_x < 2s/3 0 ≤ d_y < s	2s/3 < d_x ≤ s 0 ≤ d_y < s
misaligned scheme	DVCS	PVCS	DVCS
contrast	αR1=s2−2(dx+dy)s+2dxdy2s2 $\begin{array}{l} α_{R_{1}} = \\ \frac{s^{2} - 2 (d_{x} + d_{y}) s + 2 d_{x} d_{y}}{2 s^{2}} \end{array}$	α¯¯R2=(2s−3dx)(s−dy)4s2 $\begin{array}{l} {\bar{α}}_{R 2} = \\ \frac{(2 s - 3 d_{x}) (s - d_{y})}{4 s^{2}} \end{array}$	α¯¯R3=−(3dx−2s)(s−dy)4s2 $\begin{array}{l} {\bar{α}}_{R_{3}} = \\ - \frac{(3 d_{x} - 2 s) (s - d_{y})}{4 s^{2}} \end{array}$
recovered secret image	original color	original color	compl ementary color

lWblack area $l_{b l a c k a r e a}^{W}$ is the maximum value of the black area for a white pixel, which contains two cases (a1) and (a2), i.e.,

l W b l a c k a r e a = max {A B, a 1, A B, a 2} = max {P (A 1) + P (A 2) + P (A 3) + A' 1 + A' 2 + A' 3 + A' 4 A 1 + A 2 + A 3 + A 4 + P (A' 1, A' 2) + A' 3} = A 1 + A 2 + A 3 + A 4 + max {P (A 1) + P (A 2) + P (A 3), P (A' 1, A' 2) + A' 3} = A 1 + A 2 + A 3 + A 4 + A 1 + A 2 + A 3 = s 2 + A 1 + A 2 + A 3 = 2 s 2 - A 4 (11.5)

$\begin{array}{l} l_{b l a c k a r e a}^{W} = \max {A_{B, a 1}, A_{B, a 2}} \\ = \max {P (A_{1}) + P (A_{2}) + P (A_{3}) + {A^{'}}_{1} + {A^{'}}_{2} + {A^{'}}_{3} + {A^{'}}_{4} \\ A_{1} + A_{2} + A_{3} + A_{4} + P ({A^{'}}_{1}, {A^{'}}_{2}) + {A^{'}}_{3}} \\ = A_{1} + A_{2} + A_{3} + A_{4} + \\ \max {P (A_{1}) + P (A_{2}) + P (A_{3}), P ({A^{'}}_{1}, {A^{'}}_{2}) + {A^{'}}_{3}} \\ = A_{1} + A_{2} + A_{3} + A_{4} + A_{1} + A_{2} + A_{3} \\ = s^{2} + A_{1} + A_{2} + A_{3} \\ = 2 s^{2} - A_{4} \end{array} (11.5)$

hBblack area $h_{b l a c k a r e a}^{B}$ is the minimum value of the black area for a black pixel, which contains two cases ( b1) and ( b2), i.e.,

h B b l a c k a r e a = min {A B, b 1, A B, b 2} = s 2 + A 4 (11.6)

$h_{b l a c k a r e a}^{B} = \min {A_{B, b 1}, A_{B, b 2}} = s^{2} + A_{4} (11.6)$

l¯Wblack area ${\bar{l}}_{b l a c k a r e a}^{W}$ is the average black area for a white pixel, which contains two cases ( a1) and ( a2), i.e.,

l ¯ W b l a c k a r e a = A ¯ ¯ ¯ B , a 1 + A ¯ ¯ ¯ B , a 2 2 = 1 2 [(P (A 1) + P (A 2) + P (A 3) + A' 1 + A' 2 + A' 3 + A' 4) ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ + (A 1 + A 2 + A 3 + A 4 + P (A' 1, A' 2) + A' 3) ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯ ¯] = 1 2 [(P ¯ ¯ ¯ (A 1) + P ¯ ¯ ¯ (A 2) + P ¯ ¯ ¯ (A 3) + A' 1 + A' 2 + A' 3 + A' 4) + (A 1 + A 2 + A 3 + A 4 + P ¯ ¯ ¯ (A' 1, A' 2) + A' 3)] = s 2 + A 1 2 + A 2 2 + 3 A 3 4 (11.7)

$\begin{array}{l} {\bar{l}}_{b l a c k a r e a}^{W} = \frac{{\bar{A}}_{B, a 1} + {\bar{A}}_{B, a 2}}{2} \\ = \frac{1}{2} [\bar{(P (A_{1}) + P (A_{2}) + P (A_{3}) + {A^{'}}_{1} + {A^{'}}_{2} + {A^{'}}_{3} + {A^{'}}_{4})} \\ + \bar{(A_{1} + A_{2} + A_{3} + A_{4} + P ({A^{'}}_{1}, {A^{'}}_{2}) + {A^{'}}_{3})}] \\ = \frac{1}{2} [(\bar{P} (A_{1}) + \bar{P} (A_{2}) + \bar{P} (A_{3}) + {A^{'}}_{1} + {A^{'}}_{2} + {A^{'}}_{3} + {A^{'}}_{4}) \\ + (A_{1} + A_{2} + A_{3} + A_{4} + \bar{P} ({A^{'}}_{1}, {A^{'}}_{2}) + {A^{'}}_{3})] \\ = s^{2} + \frac{A_{1}}{2} + \frac{A_{2}}{2} + \frac{3 A_{3}}{4} \end{array} (11.7)$

h¯Bblack area ${\bar{h}}_{b l a c k a r e a}^{B}$ is the average black area for a black pixel, which contains two cases (b1) and (b2), i.e.,

h ¯ B b l a c k a r e a = A ¯ ¯ ¯ B , b 1 + A ¯ ¯ ¯ B , b 2 2 = s 2 + A 1 2 + A 2 2 + A 3 4 + A 4 (11.8)

${\bar{h}}_{b l a c k a r e a}^{B} = \frac{{\bar{A}}_{B, b 1} + {\bar{A}}_{B, b 2}}{2} = s^{2} + \frac{A_{1}}{2} + \frac{A_{2}}{2} + \frac{A_{3}}{4} + A_{4} (11.8)$

hBwhite area $h_{w h i t e a r e a}^{B}$ is the minimum value of the white area for a black pixel, which contains two cases ( b1) and (b2), i.e.,

h B w h i t e a r e a = min {A W, b 1, A W, b 2} = 0 (11.9)

$h_{w h i t e a r e a}^{B} = \min {A_{W, b 1}, A_{W, b 2}} = 0 (11.9)$

lWwhite area $l_{w h i t e a r e a}^{W}$ is the maximum value of the black area for a white pixel, which contains two cases (a1) and (a2), i.e.,

l W w h i t e a r e a = max {A W, a 1, A W, a 2} = s 2 (11.10)

$l_{w h i t e a r e a}^{W} = \max {A_{W, a 1}, A_{W, a 2}} = s^{2} (11.10)$

h¯Bwhite area ${\bar{h}}_{w h i t e a r e a}^{B}$ is the average white area for a black pixel, which contains two cases (b1) and (b2), i.e.,

h ¯ B w h i t e a r e a = A ¯ ¯ ¯ W , b 1 + A ¯ ¯ ¯ W , b 2 2 = A 1 2 + A 2 2 + 3 A 3 4 (11.11)

${\bar{h}}_{w h i t e a r e a}^{B} = \frac{{\bar{A}}_{W, b 1} + {\bar{A}}_{W, b 2}}{2} = \frac{A_{1}}{2} + \frac{A_{2}}{2} + \frac{3 A_{3}}{4} (11.11)$

l¯Wwhite area ${\bar{l}}_{w h i t e a r e a}^{W}$ is the average white area for a white pixel, which contains two cases ( a1) and ( a2), i.e.,

l ¯ W w h i t e a r e a = A ¯ ¯ ¯ W , a 1 + A ¯ ¯ ¯ W , a 2 2 = A 1 2 + A 2 2 + A 3 4 + A 4 (11.12)

${\bar{l}}_{w h i t e a r e a}^{W} = \frac{{\bar{A}}_{W, a 1} + {\bar{A}}_{W, a 2}}{2} = \frac{A_{1}}{2} + \frac{A_{2}}{2} + \frac{A_{3}}{4} + A_{4} (11.12)$

According to Definition 1 (definition of a deterministic VCS), in order to deterministically recover the secret image by its original color, the values of lWblack area $l_{b l a c k a r e a}^{W}$ and hBblack area $h_{b l a c k a r e a}^{B}$ should satisfy lWblack area<hBblack area $l_{b l a c k a r e a}^{W} < h_{b l a c k a r e a}^{B}$ . Together with Equations (11.1), (11.5), and (11.6), we get (d_x, d_y) to satisfy (s −d_x)(s −d_y) > s²/2, i.e., (d_x,d_y) falls in the region R₁. And the contrast αR1 $α_{R_{1}}$ is

α R 1 = h B b l a c k a r e a - l W b l a c k a r e a 2 s 2 = s 2 - 2 ( d x + d y ) s + 2 d x d y 2 s 2

$α_{R_{1}} = \frac{h_{b l a c k a r e a}^{B} - l_{b l a c k a r e a}^{W}}{2 s^{2}} = \frac{s^{2} - 2 (d_{x} + d_{y}) s + 2 d_{x} d_{y}}{2 s^{2}}$

Similarly, in order to recover deterministically by its complementary color, the values of hBwhite area $h_{w h i t e a r e a}^{B}$ and lWwhite area $l_{w h i t e a r e a}^{W}$ should satisfy hBwhite area>lWwhite area $h_{w h i t e a r e a}^{B} > l_{w h i t e a r e a}^{W}$ However, according to Equations (11.9) and (11.10), we get that lWwhite area $l_{w h i t e a r e a}^{W}$ does not hold. Hence, the secret image cannot be recovered deter-ministically by its complementary color.

According to Definition 2 (definition of a probabilistic VCS), in order to probabilistically recover the secret image by its original color, the values of l¯Wblack area ${\bar{l}}_{b l a c k a r e a}^{W}$ and h¯Bblack area ${\bar{h}}_{b l a c k a r e a}^{B}$ should satisfy l¯Wblack area<h¯Bblack area ${\bar{l}}_{b l a c k a r e a}^{W} < {\bar{h}}_{b l a c k a r e a}^{B}$ . Together with Equations (11.1), (11.7), and (11.8), we get (d_x,d_y) to satisfy 0 ≤ d_x < 2s/3, 0 ≤ d_y < s. By excluding the region R₁ we get to know that (d_x,d_y) falls in the region R₂. And the contrast α¯¯R2 ${\bar{α}}_{R_{2}}$ is

α ¯ ¯ R 2 = h B b l a c k a r e a - l W b l a c k a r e a 2 s 2 = ( 2 s - 3 d x ) ( s - d y ) 4 s 2

${\bar{α}}_{R_{2}} = \frac{h_{b l a c k a r e a}^{B} - l_{b l a c k a r e a}^{W}}{2 s^{2}} = \frac{(2 s - 3 d_{x}) (s - d_{y})}{4 s^{2}}$

Similarly, in order to probabilistically recover the secret image by its complementary color, the values of h¯Bwhite area ${\bar{h}}_{w h i t e a r e a}^{B}$ and l¯Wwhite area ${\bar{l}}_{w h i t e a r e a}^{W}$ should satisfy h¯Bwhite area>l¯Wwhite area ${\bar{h}}_{w h i t e a r e a}^{B} > {\bar{l}}_{w h i t e a r e a}^{W}$ . Together with Equations (11.1), (11.11), and (11.12), we get (d_x, d_y) to satisfy 2s/3 < d_x ≤ s, 0 ≤ d_y < s, i.e. (d_x, d_y) fall in the region R₃. And the contrast α¯¯R3 ${\bar{α}}_{R_{3}}$ is

α ¯ ¯ R 3 = h B b l a c k a r e a - l W b l a c k a r e a 2 s 2 = ( 3 d x - 2 s ) ( s - d y ) 4 s 2

${\bar{α}}_{R_{3}} = \frac{h_{b l a c k a r e a}^{B} - l_{b l a c k a r e a}^{W}}{2 s^{2}} = \frac{(3 d_{x} - 2 s) (s - d_{y})}{4 s^{2}}$

The above Theorem 2 is consistent with Theorem 1. According to Theorem 1 and Theorem 2, for the deviation (d_x, d_y) = (s, 0), the secret image can be probabilistically recovered by its complementary color with average contrast α¯¯=1/4. $\bar{α} = 1 / 4.$ .

The above Theorem 2 considers the deviations (d_x, d_y) less than one subpixel. In fact, when the value of d_x is between s and 2s for a misaligned (2, 2)-VCS, the secret image can also be recovered. The proof is left to the interested readers.

11.4.2 Large Subpixels Have Better Misalignment Tolerance

In this subsection, we investigate the misalignment tolerance of the large and small subpixels. And show that shares with large subpixels have better misalignment tolerance when recovering the secret image by its original color than that with small subpixels. Denote the size of the large and small subpixels as s₂ × s₂ and s₁ × s₁ respectively, where s₂ > s₁. According to Figure 11.5, the recovered secret image using the small subpixels (Figure 11.5(a)) has a higher resolution than that using the large subpixels (Figure 11.5(c)). It is observed that Figure 11.5(a) indeed has the refined resolution in detail of Lena image. We can clearly view the hair in Figure 11.5(a) but the area of hair is all black in Figure 11.5(c). The image quality using the medium-sized subpixel (Figure 11.5(b)) is between Figure 11.5(a) and Figure 11.5(c). Although using large subpixels in share has poorer resolution, it will be more robust to the misalignment error. Next, the misalignment tolerance of different-sized subpixels is formally analyzed.

Images

FIGURE 11.5
Recovered Lena images for (2,2)-VCS using the different sized subpixels: (a) the small-sized subpixel, (b) the medium-sized subpixel and (c) the large-sized subpixel.

Consider a misalignment deviation (d_x, d_y) in the (2, 2)-VCS. All the possible cases of stacked shares of a white secret pixel (1B1W) and a black secret pixel (2B0W) with a deviation (d_x, d_y) are shown in Figure 11.3. For the small subpixel (s₁ × s₁), we define the whiteness R_{W, a1} (resp. R_{W, a2}) as the ratio of black area in a stacked two-subpixel area for the case a1 (resp. a2) in Figure 11.3, and the darkness R_{B, b1} (resp. R_{B, b2}) as the ratio of the black area in a stacked two-subpixel area for the case b1 (resp. b2) in Figure 11.3. For the large subpixel (s₂ × s₂), the corresponding denotations are R′W,a1, R′W,a2, R′B,b1 ${R^{'}}_{W, a 1}, {R^{'}}_{W, a 2}, {R^{'}}_{B, b 1}$ and R′B,b2 ${R^{'}}_{B, b 2}$ .

To simplify the discussion, we only consider the one dimension deviation, i.e., (d_x, 0) or (0, d_y). Then we have the following one-dimensional deviation lemma.

Lemma 3 (One-dimensional deviation) The darkness and the whiteness ratios always satisfy R′W,a1≥RW,a1,R′W,a2≥RW,a2 R′B,b1≥RB,b1 ${R^{'}}_{W, a 1} \geq R_{W, a 1}, {R^{'}}_{W, a 2} \geq R_{W, a 2} {R^{'}}_{B, b 1} \geq R_{B, b 1}$ and R′B,b2≥RB,b2 ${R^{'}}_{B, b 2} \geq R_{B, b 2}$ for the deviations (d_x, 0) and (0, d_y) where 0 < d_x,d_y < s₁.

Proof: We only consider the case with deviation (d_x, 0) since the proof is the same for the case with deviation (0, d_y). According to equation (11.1), when d_y = 0, we have

A 1 = A' 1 = 0 A 2 = A' 2 = 0 A 3 = A' 3 = d x s A 4 = A' 4 = (s - d x) s A 3 + A 4 = s 2 (11.13)

$\begin{array}{l} A_{1} = {A^{'}}_{1} = 0 \\ A_{2} = {A^{'}}_{2} = 0 \\ A_{3} = {A^{'}}_{3} = d_{x} s \\ A_{4} = {A^{'}}_{4} = (s - d_{x}) s \\ A_{3} + A_{4} = s^{2} \end{array} (11.13)$

We consider the relation of R_{C, c} and R′C,c ${R^{'}}_{C, c}$ for C ∈ {W, B} and c ∈ (a1), (a2), (b1) and (b2). Recall that s₁ < s₂, and R_{C, C} and R′C,c ${R^{'}}_{C, c}$ can be calculated by the following formula:

R C, c = A C , c 2 s 2 1 a n d R' C, c = A C , c 2 s 2 2 (11.14)

$R_{C, c} = \frac{A_{C, c}}{2 s_{1}^{2}} a n d {R^{'}}_{C, c} = \frac{A_{C, c}}{2 s_{2}^{2}} (11.14)$

We have Table 11.4 to show the relation of R_{C, C} and R′C,c ${R^{'}}_{C, c}$ for different values of C and c.

Table 11.4 The relation of the ratios R_{C, C} and R′C,c ${R^{'}}_{C, c}$ .

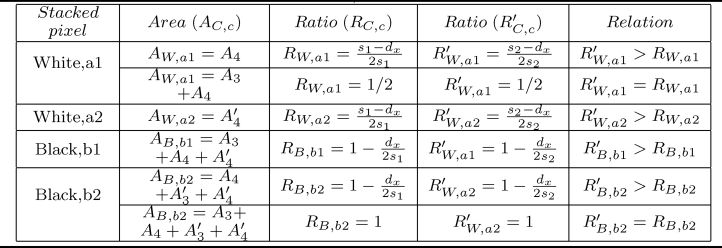
Images

The proofs of the relations in Table 11.4 are quite similar. We only take the proof of the relation between R′W,a1 ${R^{'}}_{W, a 1}$ and R_{W, a1}, for example.

According to equation (11.3), for the stacked pixel of Figure 11.3 ( a1), there are two cases of A_{W, a1}, i.e., I: A_{W, a1} = A₄ and II: A_{W, a1} = A₃ + A₄.

For the Case I, we have RW,a1=AW,a12s21=A42s21=s1−dx2s1 $R_{W, a 1} = \frac{A_{W, a 1}}{2 s_{1}^{2}} = \frac{A_{4}}{2 s_{1}^{2}} = \frac{s_{1} - d_{x}}{2 s_{1}}$ and R′W,a1=s2−dx2s2 ${R^{'}}_{W, a 1} = \frac{s_{2} - d_{x}}{2 s_{2}}$ , by subtraction we have R′W,a1−RW,a1=s2−dx2s2−s1−dx2s2−s1−dx2s1=dx(s2−s1)2s1s2>0 ${R^{'}}_{W, a 1} - R_{W, a 1} = \frac{s_{2} - d_{x}}{2 s_{2}} - \frac{s_{1} - d_{x}}{2 s_{2}} - \frac{s_{1} - d_{x}}{2 s_{1}} = \frac{d_{x} (s_{2} - s_{1})}{2 s_{1} s_{2}} > 0$ , i.e. R′W,a1>RW,a1 ${R^{'}}_{W, a 1} > R_{W, a 1}$ .

For the Case II, we have R′W,a1−RW,a1=s222s22−s212s21=0 ${R^{'}}_{W, a 1} - R_{W, a 1} = \frac{s_{2}^{2}}{2 s_{2}^{2}} - \frac{s_{1}^{2}}{2 s_{1}^{2}} = 0$ , i.e. R′W,a1=RW,a1 ${R^{'}}_{W, a 1} = R_{W, a 1}$ .

According to Table 11.4, the lemma follows. □

According to Lemma 3, for one-dimensional deviation, it is evident that if R′W≥RW ${R^{'}}_{W} \geq R_{W}$ and R′B≥RB ${R^{'}}_{B} \geq R_{B}$ , the whiteness of the white secret pixel is whiter and the darkness of the black secret pixel is darker when using the large subpixels. We can conclude that the large subpixels have better misalignment tolerance than that of small subpixels. Actually, for two-dimensional deviation, the conclusion also holds. However, the proof is rather complex; we omit the proof here. Readers also can reach this conclusion via simulations, for example the Figure 11.6, and more simulations for two-dimensional deviation can be found in [16].

Images

FIGURE 11.6
Recovered secret image for a (2, 2)-VCS using two different-sized subpixels and (d_x ,d_y ) = (0.5, 0.5), (s₁/s₂) = 2: (a) the small subpixel and (b) the large subpixel; two secret image (a printed text ”VSS” and a halftoned Lena image) are tested.

From the preceding description and the results in Figure 11.5 and Figure 11.6, unfortunately, there exists another dilemma of using the large or small subpixels. Together with previous comparisons in Table 11.1, we summarize the advantages and disadvantages of large and small subpixels in Table 11.5.

In order to bring these conflicting goals in a kind of balance, we properly distribute two-sized subpixels in shares to develop their specialities and simultaneously avoid corresponding disadvantages. Our method is based on the trade-off between the usage of large and small subpixels. Both two-sized subpixels create a trade-off, which a large size subpixel leads to the high misalignment tolerance but the low resolution, while the small subpixel has the opposite properties. Finally, we successfully reduce the difficulty of aligning shares. Designing our misalignment tolerant VCS therefore delivers the following problems: (1) What is the appropriate percentage of the large subpixel in a share? (2) What is the appropriate size ratio of the large subpixel to the small subpixel? (3) How do we arrange the large and small subpixels in one share?

Table 11.5 The advantages and disadvantages of large and small subpixels.

size of the subpixels	advantages	disadvantages
larger	easier to align and better misalignment tolerance	larger transparency size and lower resolution
smaller	smaller transparency size and higher resolution	harder to align and worse misalignment tolerance

11.5 A Misalignment Tolerant VCS

11.5.1 The Algorithm

Concerning the first two problems, both items (the percentage and the size ratio) can be used to trade the quality of the recovered secret image for the misalignment tolerance. Different percentages and size ratios will be experimented and analyzed in Section 11.5.2. Consider the third problem, how to arrange the large and small subpixels in one share. In this chapter, we arrange them in a regular mask or a random mask. Subsequently, we describe the encrypting/decrypting algorithm of a (k, n)-threshold misalignment tolerant VCS, when given a percentage (the item in Problem (1)), a size ratio (the item in Problem 2) and an arrangement mask (the item in problem (3)).

Notation Used:

I A gray secret image of size × × y.

γ² The size ratio of a large to a small subpixel, i.e., γ² = (s₂/s₁)².

I_S A small-scaled secret image of size × × y. This image is obtained by halftoning I into a binary image. Note that, this image is used for embedding small subpixels.

I_B A large-scaled secret image of size (x/γ) × (y/γ). This image is obtained by reducing the secret image I to size (x/γ) × (y/γ) and then halftoning to a binary image. Note that, this image is used for embedding large subpixels.

P_B (p_S) V_B and p_S are percentages of large and small subpixels, respectively.

M_reg A regular mask of size (x/γ) × (y/γ). This mask is only designed for p_B = p_s = 50%. Figure 11.7(a) shows the regular mask with the alternate blocks, and , where a block contains large subpixels and a block contains small subpixels.

M_ran A random mask of size (x/γ) × (y/γ). This mask is designed for any p_B and p_s. At this time, and are randomly chosen according p_B and p_s, as shown in Figure 11.7(b).

D_B (∙) Let A = [a_{i, j}] , where a_{i, j} is the element of the i-th row and j-th column in A, be a matrix in C₁ or C₀. The function D_B(∙) divides a secret pixel s into m large subpixels (bp)ij((bp)ij=0 ${(b p)}_{j}^{i} {((b p)}_{j}^{i} = 0$ denotes white and (bp)ij=1 ${(b p)}_{j}^{i} = 1$ denotes black) in the i-th share, 1 ≤ i ≤ n and 1 ≤ j ≤ m, defined as follows:

D B (s) = {(b p) i j = a i, j in A \in C 0 for s is the white secret pixel . (b p) i j = a i, j in A \in C 1 for s is the white secret pixel .

$D_{B} (s) = {\begin{array}{l} {(b p)}_{j}^{i} = a_{i, j} in A \in C_{0} for s is the white secret pixel . \\ {(b p)}_{j}^{i} = a_{i, j} in A \in C_{1} for s is the white secret pixel . \end{array}$

D_s(∙) Similar to D_B(∙), it divides a secret pixel into m small subpixels (sp)ij ${(s p)}_{j}^{i}$ in the i-th share, 1 ≤ i ≤ n and 1 ≤ j ≤ m.

Amx,my(⋅) $A_{m_{x}, m_{y}} (\cdot)$ Arrangement function that randomly arranges m large (or small) subpixels into an ( m_x × m_y)-sized rectangle where m = m_x × m_y.

O⁽ⁱ⁾ n output shares, i ∈ [1, n], of size (x × m_x) × (y × m_y).

I' The recovered secret image of size (x × m_x) × (y × m_y).

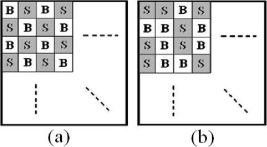
Images

FIGURE 11.7
Regular and random masks for arranging the large and small subpixels: (a) regular mask and (b) random mask.

Even though the shares use a regular mask, an attacker could not gain any information from the mask and the secrecy is not compromised.

Encrypting Algorithm:

Input: I, γ², p_B, p_s, C₀ and C₁ of a (k, n)-threshold VCS.

Output: O⁽ⁱ⁾, i ∈ [1,n].

Step 1: Obtain the large-scaled and small-scaled secret images I_B and I_s from a secret image I.

Step 2: Use p_B and p_S to generate the M_ran mask or choose the M_reg mask for the case p_B = p_S = 50%; let the chosen mask M = M_ran or M_reg.

Step 3: For each block in the mask M, do the following:

Step 3-1: If the block is the large block , for the secret pixel ”s” in the corresponding block of the large-scaled image I_B, do the following:

Assign (bp)ij=DB(s) ${(b p)}_{j}^{i} = D_{B} (s)$ for i ∈ [1,n] and j ∈ [1, m];

Use Amx,my((bp)ij) $A_{m_{x}, m_{y}} ({(b p)}_{j}^{i})$ to create n (m_x × m_y)-sized rectangles, where m = m_x × m_y, and deliver them in the corresponding block to O⁽¹⁾, O⁽²⁾, …, O⁽ⁿ⁾, respectively.

Step 3-2: If the block is the large block , for the secret pixel ”s” in the corresponding block of the large-scaled image I_S, do the following:

Assign (bp)ij=DS(s) ${(b p)}_{j}^{i} = D_{S} (s)$ for i ∈ [1, n] and j ∈ [1, m];

Use Amx,my((sp)ij) $A_{m_{x}, m_{y}} ({(s p)}_{j}^{i})$ to create n (m_x × m_y)-sized rectangles, where m = m_x × m_y, and deliver them in the corresponding block to O⁽¹⁾, O⁽²⁾, …, O⁽ⁿ⁾, respectively.

Decrypting Algorithm:

Input: Any k shares from O⁽ⁱ⁾, i ∈ [1, n].

Output: I′.

Step 1: Print out k shares on transparencies. Stack and align them by hand with the approximate accuracy.

/* Note that, when stacking shares the tradition VCS needs the precise alignment; the proposed scheme has the misalignment tolerance and so that one just aligns them roughly. */

Step 2: Decrypt the secret directly by human eyes.

Step 3: Align shares gradually to get a refined secret image of I′.

/* One can first align transparencies precisely in the vertical direction, and then move gradually by hand without losing the secret in the horizontal direction, finally the recovered secret image with no deviation can be obtained.*/

For easily understanding the encrypting algorithm, we herein give an example to show how to encode a secret image.

Example 4 Construct two shares by the (2, 2) misalignment tolerant VCS, where p_B = p_S = 50%, γ² = 4, and M_reg are used. We use a 16 × 16-pixel secret image I, one black horizontal on a white background (Figure 11.8).

Since I is black and white now, so I_S = I, and I_B has the size of 8 × 8 pixels shown in Figure 11.8(a) and (b). By using M_reg (Figure 11.7(a)), we encrypt the first pixel in I_B, which is a white secret pixel. Suppose the white pixel is divided into two subpixels (■□) in the first share O⁽¹⁾ and the corresponding two subpixels in the second share O⁽²⁾ are also (■□). Subsequently, encrypt four small secret pixel in Is (see Figure 11.8(c)), these four white secret pixels are respectively encrypted into and in O⁽¹⁾ and O⁽²⁾. According to the M_reg mask, encrypt all secret pixels in I_B and I_S. Finally, we obtain two shares O⁽¹⁾ and O⁽²⁾ of 32 × 16 pixels.

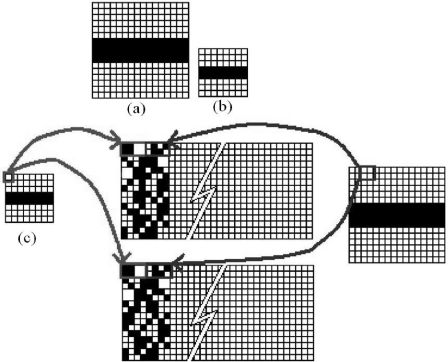
Images

FIGURE 11.8
Encrypt a 16 × 16-pixel secret image by using a (2, 2) misalignment VCS, where p_B = p_s = 50%, γ² = 4, and M_reg are used: (a) the small-scaled secret image I_S,(b) the large-scaled secret image I_B, and (c) two shares O⁽¹⁾ and O⁽²⁾.

11.5.2 Simulations

In this section, we give some simulations to show the performance of the misalignment tolerant VCS for different deviations, size ratios, percentages, and masks. Example 5 uses fifty-fifty large and small subpixels with regular and random masks, respectively, such that we can try out the performance of the mask. In Example 6, we use different size ratios to study how the size ratio affects the visual quality and the misalignment tolerance.

Example 5 Construct the (2, 2) misalignment tolerant VCS, where p_B = p_S = 50% and γ² = 16. Regular mask M_reg and random mask M_ran are tested, respectively. The printed-text ”VSS”is used as a secret image.

Images

FIGURE 323.11
Recovered secret images for a (2, 2) misalignment VCS using two-sized subpixels of γ² = 16: (a) p_B = 0%, (b) p_B = p_S = 50%, M_reg, (c) p_B = p_S = 50%, M_ran and (d) p_B = 100%, horizontal deviations: 0, 0.5, 1, and 2 are tested (unit: small subpixel).

Use the deviations (0, 0), (0.5,0), (1, 0), (1.5, 0) and (2, 0) to test the misalignment tolerance of the following four schemes: (a) p_B = 0%, (b) P_B = p_S = 50%, M_reg, (c) p_B = p_S = 50%, M_ran and (d) p_B = 100%. Notice that (a) and (d) are just the traditional VCS with all small subpixels and large subpixels, respectively. The first scheme has the best resolution when aligning correctly, as shown in Figure 11.9 (a1), but the secret on the recovered secret image diminishes quickly when the deviation increases. The secret becomes invisible when the deviation is large enough (see Figure 11.9 (a5)). Comparing Figure 11.9 (a) and (d), the small subpixel gives the high resolution (see Figure 11.9 (a1) and (d1)), whereas the large subpixel enhances the misalignment tolerance. For example, the deviation is (d_x, d_y) = (2, 0), the secret in Figure 11.9 (a5) becomes invisible but we still visually view the secret ”VSS” in Figure 11.9 (d5). As shown in Figure 11.9 (a3) and (a4), the secret image is recovered by its complementary color. This interesting phenomenon is compatible with the result in Section 11.3 and Section 11.4. From these stacked results, our two-sized subpixel approach actually provides the misalignment tolerance. Also, it is observed that Figure 11.9 (b) (M_reg) has the better visual quality than Figure 11.9 (c) (M_ran). This result is anticipated because the random arrangement of subpixels will introduce additional noise to the recovered secret image.

Example 6 Consider the first scheme in Example 5 (a (2, 2) misalignment tolerant VCS that the large and small subpixels are half used, respectively, and regularly arranged in a share). Three size ratios, γ² = 4, 16, and 64, are tested. The printed-text ”VSS” is used as a secret image.

Images

FIGURE 11.10
Recovered secret images for a (2, 2) misalignment tolerant VCS using p_B = p_S = 50%, M_reg and three size ratios: (a) γ² = 4, (b) γ² = 16 and (c) γ² = 64, horizontal deviations: 0, 0.5, 1, 1.5, 2, 2.5, 3, and 3.5 are tested (unit: small subpixel).

Figure 11.10 (a–c) reveal the recovered secret images for γ² = 4, 16, and 64, respectively. The clearness of the recovered secret image diminishes when the misalignment increases. The misalignment tolerant VCS using γ² = 64 has the best misalignment tolerant capability, whereas it has the worst visual quality for no deviation. On the contrary, the misalignment tolerant VCS using γ² =4 has a different characteristic. We may trade the misalignment tolerance for the image quality by the size ratio.

11.6 Conclusions and Discussions

This chapter is intended to show some recent results about the alignment problem of the VCS. We considered two kinds of misalignment, (1) misalignment with integer number of subpixels and (2) misalignment with less than one subpixel. In both cases, the secret image can be visually recovered. This phenomenon indicates that, the VCS, by itself, has some misalignment tolerance.

Then we compared the misalignment tolerance of large and small subpixels, and showed that the large subpixel had better misalignment tolerance. Based on this result, a misalignment tolerant VCS was given that traded the large and small subpixels in one share. Simulations were provided to show the performance of the misalignment tolerant VCS.

Because of the page limit, we cannot introduce more misalignment tolerant VCS. Interested readers can find more information about the alignment problem of the VCS in the following papers [8, 16, 13, 6, 9].

11.7 Acknowledgments

I gratefully acknowledge Prof. Chuankun Wu, as he introduced me to visual cryptography. We shared many pleasant memories on studying visual cryptography. This work was supported by NSFC grant No. 60903210.

Bibliography

[1] G. Ateniese, C. Blundo, A. De Santis, and D.R. Stinson. Visual cryptography for general access structures. In Information and Computation, volume 129, pages 86–106, 1996.

[2] G. Ateniese, C. Blundo, A. De Santis, and D.R. Stinson. Extended capabilities for visual cryptography. In ACM Theoretical Computer Science, volume 250 Issue 1-2, pages 143–161, 2001.

[3] E. Biham and A. Itzkovitz. Visual cryptography with polarization. In the Dagstuhl Seminar on Cryptography, September 1997, and in the RUMP Session of CRYPTO’98, 1997.

[4] S. Cimato, R. De Prisco, and A. De Santis. Probabilistic visual cryptography schemes. In The Computer Journal, volume 49, Number 1, pages 97–107, 2006.

[5] S. Droste. New results on visual cryptography. In CRYPTO ’96, Springer-Verlag LNCS, volume 1109, pages 401–415, 1996.

[6] K. Kobara and H. Imai. Limiting the visible space visual secret sharing schemes and their application to human identification. In ASIACRYPT ’96, Springer-Verlag LNCS, volume 1163, pages 185–195, 1996.

[7] H. Kuwakado and H. Tanaka. Size-reduced visual secret sharing scheme. In IEICE Transactions on Fundamentals, volume E87-A, No. 5, pages 1193–1197, 2004.

[8] F. Liu, C.K. Wu, and X.J. Lin. The alignment problem of visual cryptography schemes. In Designs, Codes and Cryptography, volume 50, pages 215–227, 2009.

[9] M. Nakajima and Y. Yamaguchi. Enhancing registration tolerance of extended visual cryptography for natural images. In Journal of Electronic Imaging, volume 13, pages 654–662, 2004.

[10] M. Naor and A. Shamir. Visual cryptography. In EUROCRYPT ’94, Springer-Verlag Berlin, volume LNCS 950, pages 1–12, 1995.

[11] R. Ito, H. Kuwakado, and H. Tanaka. Image size invariant visual cryptography. In IEICE Transactions on Fundamentals of Electronics, Communications and Computer Science, volume E82-A, No. 10, pages 2172–2177, 1999.

[12] S. J. Shyu. Efficient visual secret sharing scheme for color images. In Pattern Recognition, volume 39, pages 866–880, 2006.

[13] W.Q. Yan, D. Jin, and M.S. Kankanhalli. Visual cryptography for print and scan applications. In Proceedings of the 2004 International Symposium on Circuits and Systems, volume 5, pages 572–575, 2004.

[14] C.N. Yang. New visual secret sharing schemes using probabilistic method. In Pattern Recognition Letters, volume 25, pages 481–494, 2004.

[15] C.N. Yang and C.S. Laih. New colored visual secret sharing schemes. In Designs, Codes and Cryptography, volume 20, pages 325–335, 2000.

[16] C.N. Yang, A.G. Peng, and T.S. Chen. Mtvss:(m)isalignment (t)olerant (v)isual (s)ecret (s)haring on resolving alignment difficulty. In Signal Processing, volume 89, pages 1602–1624, 2009.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for
11 Resolving the Alignment Problem in Visual Cryptography

11

Resolving the Alignment Problem in Visual Cryptography

CONTENTS

11.1 Introduction

11.2 Preliminaries

11.3 Misalignment with Integer Number of Subpixels

11.4 Misalignment with Less Than One Subpixel

11.4.1 Shares with Slightly Misalignment Can Still Recover the Secret Image

11.4.2 Large Subpixels Have Better Misalignment Tolerance

11.5 A Misalignment Tolerant VCS

11.5.1 The Algorithm

11.5.2 Simulations

11.6 Conclusions and Discussions

11.7 Acknowledgments

Bibliography

Table of Contents for 11 Resolving the Alignment Problem in Visual Cryptography

Create new playlist

Sign In

Sign Up

CONTENTS

Table of Contents for
11 Resolving the Alignment Problem in Visual Cryptography