Section 5.2 Systems of Linear Equations in Three Variables

Before Starting this Section, Review

  1. 1 Solving a system of equations in two variables (Section 5.1 )

Objectives

  1. 1 Solve a system of linear equations in three variables.

  2. 2 Classify systems as consistent and inconsistent.

  3. 3 Solve nonsquare systems.

  4. 4 Interpret linear systems in three variables geometrically.

  5. 5 Use linear systems in applications.

CAT Scans

Computerized axial tomography imaging is more commonly known as a “CAT scan” or “CT scan.” Tomography is from the Greek word tomos, meaning “slice or section,” and graphia, meaning “describing.” The CAT scan machine was invented in 1972 by British engineer Godfrey Hounsfield and, independently, by physicist Allan Cormack of Tufts University in Massachusetts. Hounsfield never attended a university, but he started experimenting with electrical and mechanical devices as a boy. He shared a Nobel Prize in 1979 with Cormack for inventing the scanner technology and was honored with knighthood in England for his contributions to medicine and science. CAT scanners use X-rays measured outside the patient’s body, together with algebraic computations, to construct pictures of the patient’s internal body organs, including the brain. The scanner does not “take” any pictures; instead, it computes pictures. The idea behind the CAT scanner is simple. When an X-ray passes through an object, it loses intensity. The denser the object, the more intensity the X-ray loses. Because tumors are denser than healthy tissues, an unexpected loss of intensity may indicate the presence of a tumor. To obtain sufficient information, a large number of properly arranged X-rays is needed. Imagine a cross section of body tissue with a superimposed mathematical grid. Each region bounded by the grid lines is called a grid cell. In an actual CAT scan, each grid cell is 2 square millimeters and contains 10,000 or more biological cells. The grid shown in Figure 5.6 would require many X-rays. Actual CAT scanners work with grids that have 512×512512×512 grid cells and require hundreds of thousands of X-ray beams. In Example 6, we discuss a simple situation in which X-rays pass through three grid cells.

Figure 5.6

Cross section with tumor

Adapted with permission from Mathematics Teacher, May 1996. © 1996 by the National Council of Teachers of Mathematics.

Systems of Linear Equations

  1. 1 Solve a system of linear equations in three variables.

A linear equation in the variables x1, x2, …, xn is an equation that can be written in the form

a1x1+a2x2+⋯+anxn=b,

where b and the coefficients a1, a2, …, an are real numbers. The subscript n can be any positive integer. When n is small—say, between 2 and 5 (as in most textbook examples and exercises)—we normally use x, y, z, u, and v instead of x1, x2, x3, x4, and x5. However, in real-life applications, n might be 100 or 1000 or even greater.

A system of linear equations (or a linear system) in three variables is a collection of two or more linear equations involving the same three variables. For example,

{x+3y+z=02x−y+z=53x−3y+2z=10

is a system of three linear equations in the three variables x, y, and z. An ordered triple (a, b, c) is a solution of a system of three linear equations in three variables x, y, and z. if each equation in the system is a true statement when a, b, and c are substituted for x, y, and z, respectively.

Example 1 Verifying a Solution

Determine whether the ordered triple (2, −1, 3) is a solution of the following linear system.

{5x+3y−2z=1(1)x−y+z=6(2)2x+2y−z=−1(3)

Solution

We replace x with 2, y with −1, and z with 3 in all three equations.

Equation (1)Equation (2)Equation (3)5x+3y−2z=15(2)+3(−1)−2(3)?=110−3−6?=11=1✓x−y+z=62−(−1)+3?=62+1+3?=66=6✓2x+2y−z=−12(2)+2(−1)−(3)?=−14−2−3?=−1−1=−1✓

Because the ordered triple (2, −1, 3) satisfies all three equations, it is a solution of the system.

Practice Problem 1

  1. Determine whether the ordered triple (2, −3, 2) is a solution of the following linear system.

    {x+y+z=13x+4y+z=−42x+y+2z=5

We will now use a procedure called Gaussian elimination to convert a system of three equations in the variables x, y, and z into an equivalent system in triangular form with leading coefficient 1, as shown below.

{x+ay+bz=p(1)y+cz=q(2)z=z0(3)

We can then solve the system by back-substitution. To get a system in triangular form, we use the following three operations to obtain equivalent systems (systems with the same solution set as the original system).

Practice Problem 2

  1. Solve the system.

    {2x+5y=1x−3y+2z=1−x+2y+z=7

Number of Solutions of a Linear System

  1. 2 Classify systems as consistent and inconsistent.

As in the case of two variables, a system of linear equations in three variables may be consistent (having at least one solution) or inconsistent (having no solution). The equations in a consistent system may be dependent (the system has infinitely many solutions) or independent (the system has one solution).

Example 3 Attempting to Solve a Linear System with No Solution

Solve the system of equations.

{x−y+2z=5(1)2x+y+z=7(2)3x−2y+5z=20(3)

Solution

  1. Steps 1–2 To eliminate x from equation (2), add −2 times equation (1) to equation (2).

    −2x+2y−4z=−102x+y+z=73y−3z=−3(2)(4)−2(x−y+2z=5)Add.

    Next, we eliminate x from equation (3) using equations (1) and (3).

    −3x+3y−6z=−153x−2y+5z=20y−z=5(3)(5)−3(x−y+2z=5)Add.

    We now have the equivalent system:

    {x−y+2z=5(1)3y−3z=−3(4)y−z=5(5)

  2. Step 3 Multiply equation (4) by 13 to obtain

    y−z=−1(6)

    We can eliminate y in equation (5) using equation (6).

    −y+z=1y−z=50=6(5)(7)−1(y−z=−1)Add.

    We now have the system in triangular form:

    {x−y+2z=5y−z=−1(1)(6)0=6︸(7)false

    This system is equivalent to the original system. Because equation (7) is false, we conclude that the solution set of the system is ∅ and the system is inconsistent.

Practice Problem 3

  1. Solve the system of equations.

    {2x+2y+2z=12−3x+y−11z=−62x+y+4z=−8

Side Note

An alternate method for Step 3 is to solve the 2×2 system of equations (4) and (5), then back-substitute into equation (1) to solve for the third variable.

Example 4 Solving a System with Infinitely Many Solutions

Solve the system of equations.

{x−y+z=7(1)3x+2y−12z=11(2)4x+y−11z=18(3)

Solution

  1. Steps 1–2 Eliminate x using equations (1) and (2).

    −3x+3y−3z=−213x+2y−12z=115y−15z=−10(2)(4)−3(x−y+z=7)Add.

    Eliminate x using equations (1) and (3).

    −4x+4y−4z=−284x+y−11z=185y−15z=−10(3)(5)−4(x−y+z=7)Add.

    We now have the following equivalent system:

    {x−y+z=7(1)5y−15z=−10(4)5y−15z=−10(5)

  2. Step 3 We eliminate y using equations (4) and (5).

    −5y+15z=105y−15z=−100=0(5)(6)−1(5y−15z=−10)Add.

    We finally have the system in triangular form:

    {x−y+z=75y−15z=−10(1)(4)0=0︸(6)True

    The equation 0=0 is equivalent to 0 z=0, which is true for every value of z. Solving equation (4) for y, we have y=3z−2. Substituting y=3z−2 into equation (1) and solving for x, we obtain

    x=y−z+7Solve equation (1) for x.x=(3z−2)−z+7Substitute y=3z−2.x=2z+5Simplify.

    Thus, for every real number z, the triple (x, y, z)=(2z+5, 3z−2, z) is a solution of the system. For example, when z=0, the triple (5, −2, 0) is a solution. When z=1, the triple (7, 1, 1) is a solution. Therefore, the given system has infinitely many solutions, one for each real number z, and the equations are dependent. The solution set for the system is {(2z+5, 3z−2, z)}.

Practice Problem 4

  1. Solve the system of equations.

    {x+y+z=5−4x−y−8z=−292x+5y−2z=1

Nonsquare Systems

  1. 3 Solve nonsquare systems.

Sometimes in a linear system, the number of equations is not the same as the number of variables. Such systems are called nonsquare linear systems.

Example 5 Solving a Nonsquare Linear System

Solve the system of linear equations.

{x+5y+3z=7(1)2x+11y−4z=6(2)

Solution

  1. Steps 1–2 We eliminate x using equations (1) and (2).

    −2x−10y−6z=−142x+11y−4z=6y−10z=−8(2)(3)−2(x+5y+3z=7)Add.

    We obtain the equivalent system:

    {x+5y+3z=7(1)y−10z=−8(3)

  2. Steps 3–4 Because there is no third equation, Steps 3 and 4 are not needed.

  3. Step 5 Solve equation (3) for y in terms of z to obtain

    y=10z−8.

  4. Step 6 Back-substitute y=10z−8 into equation (1) and solve for x.

    x+5y+3z=7Equation (1)x+5(10z−8)+3z=7Replace y with 10z−8.x=−53z+47Solve for x.

Steps 5 and 6 mean that z determines both the x- and y-values. The system has infinitely many solutions, one for each real number z. The solution set is {(−53z+47, 10z−8, z)}.

Practice Problem 5

  1. Solve the system of linear equations.

    {x+3y+2z=42x+7y−z=5

Geometric Interpretation

  1. 4 Interpret linear systems in three variables geometrically.

The graph of a linear equation in three variables, such as ax+by+cz=d (where a, b, and c are not all zero), is a plane in three-dimensional space. Figure 5.7 shows possible situations for a system of three linear equations in three variables.

Figure 5.7

  1. Three planes intersect in a single point. The system has only one solution.

  2. Three planes intersect in one line. The system has infinitely many solutions.

  3. Three planes coincide with each other. The system has infinitely many solutions.

  4. There are three parallel planes. The system has no solution.

  5. Two parallel planes are intersected by a third plane. The system has no solution.

  6. Three planes have no point in common. The system has no solution.

An Application to CAT Scans

  1. 5 Use linear systems in applications.

CAT scanners report X-ray data in units called linear attenuation units (LAUs), also called Hounsfield numbers. The data are reported in such a way that if an X-ray passes through consecutive grid cells, the total weakening of the beam is the sum of the individual decreases. Table 5.1 gives the range of LAUs that determine whether the grid cell contains healthy tissue, tumorous tissue, a bone, or a metal.

Table 5.1 CAT Scanner Ranges

Reprinted with permission from Mathematics Teacher, May 1996. © 1996 by the National Council of Teachers of Mathematics.

Type of Tissue LAU Values
Healthy tissue 0.1625–0.2977
Tumorous tissue 0.2679–0.3930
Bone 0.38757–0.5108
Metal 1.54−∞

Example 6 A CAT Scan with Three Grid Cells

Let A, B, and C be three grid cells, as shown in Figure 5.8. A CAT scanner reports the following data for a patient named Monica.

Figure 5.8

Reprinted with permission from Mathematics Teacher, May 1996. © 1996 by the National Council of Teachers of Mathematics

  1. Beam 1 is weakened by 0.80 unit as it passes through grid cells A and B.

  2. Beam 2 is weakened by 0.55 unit as it passes through grid cells A and C.

  3. Beam 3 is weakened by 0.65 unit as it passes through grid cells B and C.

Use Table 5.1 to determine which grid cells contain each type of tissue listed.

Solution

Suppose grid cell A weakens the beam by x units, grid cell B weakens it by y units, and grid cell C weakens it by z units. Then we have the system:

{x+y=0.80(1)(Beam 1)x+z=0.55(2)(Beam 2)y+z=0.65(3)(Beam 3)

To solve this system of equations, we use the elimination procedure. Subtracting equation (1) from equation (2), we obtain the equivalent system:

{x+y=0.80(1)−y+z=−0.25(4)Subtract equation (1) from equation (2).y+z=0.65(3)

Add equation (4) to equation (3) to get the system:

{x+y=0.80(1)−y+z=−0.25(4)2z=0.40(5)Add equation (4) to equation (3).

Multiply equation (5) by 12 to obtain z=0.20. Then back-substitute z=0.20 in equation (4) to get −y+0.20=−0.25, or y=0.45. Next, back-substitute y=0.45 in equation (1) to get x+0.45=0.80. Solving for x gives x=0.35. Now referring to Table 5.1, we conclude that cell A contains tumorous tissue (because x=0.35), cell B contains a bone (because y=0.45), and cell C contains healthy tissue (because z=0.20).

Practice Problem 6

  1. In Example 6, suppose (i) Beam 1 is weakened by 0.65 unit as it passes through grid cells A and B, (ii) Beam 2 is weakened by 0.70 unit as it passes through grid cells A and C, and (iii) Beam 3 is weakened by 0.55 unit as it passes through grid cells B and C. Use Table 5.1 to determine which grid cells contain each type of tissue listed.

Section 5.2 Exercises

Concepts and Vocabulary

  1. Systems of equations that have the same solution set are called                           systems.

  2. Adding a(n)                           multiple of one equation to another equation in the system produces an equivalent system.

  3. If any of the equations in a system has no solution, then the system is                           .

  4. If the number of equations is different from the number of variables in a linear system, then the system is called a(n)                           system.

  5. True or False. The graph of the equation x−2y+z=1 is a plane in three-dimensional space.

  6. True or False. If {(2z, 1−z, z+3)} is the solution set of a linear system in three variables, then (0, 1, 3) is a solution of this system.

  7. True or False. If in the process of converting a linear system to triangular form an equation of the form 0=k occurs, with k≠0, then the system has exactly one solution.

  8. True or False. A dependent system of linear equations has no solutions.

Building Skills

In Exercises 9–12, determine whether the given ordered triple is a solution of the given linear system.

  1. {2x−2y−3z=13y+2z=−1(1, −1, 1)y+z=0

  2. {3x−2y+z=2y+z=5(2, 3, 2)x+3z=8

  3. {x+3y−2z=02x−y+4z=5(−10, 8, 7)x−11y+14z=0

  4. {x−4y+7z=143x+8y−2z=13(4, 1, 2)7x−8y+26z=5

In Exercises 13–16, solve each triangular linear system.

  1. x+y+z=4y−2z=4z=−1

     

  2. x+3y+2z=3y+2z=8z=5

  3. x−5y+3z=−1y−2z=−6z=4

  4. x+3y+5z=0y+7z=2z=12

     

  5. In the system in Exercise 9, interchange equations (2) and (3). Write the new equivalent system. In the new system, eliminate y from the last equation. Convert the system to triangular form.

  6. In Exercise 10, interchange equations (1) and (3). In the new equivalent system, eliminate x from the last equation. Convert the system to triangular form.

  7. Convert the system of Exercise 11 to triangular form.

  8. Convert the system of Exercise 12 to triangular form.

In Exercises 21–24, convert the system to triangular form and then use back-substitution to solve the system.

  1. {x−y+z=62y+3z=52z=6

  2. {4x+5y+2z=−33y−z=14−3z=15

  3. {4x+4y+4z=73x−8y=144z=−1

  4. {5x+10y+10z=02y+3z=−0.64z=1.6

In Exercises 25–46, find the solution set of each linear system. Identify inconsistent systems and dependent equations. For dependent equations, write your answer as in Example 4.

  1. {x+y+z=6x−y+z=22x+y−z=1

  2. {x+y+z=62x+3y−z=53x−2y+3z=8

  3. {2x+3y+z=9x+2y+3z=63x+y+2z=8

  4. {4x+2y+3z=6x+2y+2z=12x−y+z=−1

  5. {x−4y+7z=143x+8y−2z=137x−8y+26z=5

  6. {x+y+4z=6x+2y−2z=87x+10y+10z=60

  7. {2x+3y+2z=7x+3y−z=−2x−y+2z=8

  8. {x−y+2z=32x+2y+z=3x+y+3z=4

  9. {4x−2y+z=52x+y−2z=4x+3y−2z=6

  10. {x−3y+2z=92x+4y−3z=−93x−2y+5z=12

  11. {2x+y+z=6x+y−z=1x+y+2z=4

  12. {2x+y−3z=7x−y−2z=43x+3y+2z=4

  13. {x−y−z=3x+9y+z=32x+3y−z=6

  14. {x+y−z=23x−y−z=103x+y−2z=8

  15. {x+y=0y+2z=−4y+z=4−x

  16. {2x+4y+3z=6x+2z=−1x−2y+z=−5

  17. {2y−z=−4x+z=32x+3y=−1

  18. {x+y=92y+3z=7x−2z=4

  19. {3x−2z=112x+y=82y+3z=1

  20. {2x+y=4x+2z=33y−z=5

  21. {2x+6y+11=06y−18z+1=0

  22. {3x+5y−15=06x+20y−6z=11

Applying the Concepts

In Exercises 47–54, use a system of equations to solve each problem.

  1. Investment. Miguel invested $20,000 in three different funds that paid 4%, 5%, and 6% for the year. The total income for the year from the three funds was $1060. The income from the 6% fund was twice the income from the 5% fund. What amount was invested in each fund?

  2. Number problem. The sum of the digits in a three-digit number is 14. The sum of the hundreds digit and the units digit is equal to the tens digit. If the hundreds digit and the units digit are interchanged, the number is increased by 297. What is the original number?

  3. Election campaign. Alex, Becky, and Courtney volunteered to stuff 741 envelopes with newsletters for Senator Douglas’s reelection campaign. Alex could assemble 124 per hour; Becky, 118 per hour; and Courtney, 132 per hour. They worked a total of 6 hours. The sum of the number of hours that Becky and Courtney spent was twice what Alex spent. How long did each of them work?

  4. Age of students. A college algebra class of 38 students at Central State College was made up of people who were 18, 19, and 20 years of age. The average of their ages was 18.5 years. How many of each age were in the class if the number of 18-year-olds was eight more than the combined number of 19- and 20-year-olds?

  5. Coins in a machine. A vending machine’s coin box contains nickels, dimes, and quarters. The total number of coins in the box is 300. The number of dimes is three times the number of nickels and quarters together. If the box contains $30.05, find the number of nickels, dimes, and quarters that it contains.

  6. Sports. The Wildcats scored 46 points in a football game. Twice the number of points resulting from the sum of field goals and extra points equals two more than the number of points from touchdowns. Five times the number of points scored by field goals equals twice the number of points from touchdowns. Find the number of points resulting from touchdowns, field goals, and extra points. [A touchdown =6 points, a field goal =3 points, and an extra point =1 point.]

  7. Weekly wage. Amy worked 53 hours one week and was paid at three different rates. She earned $7.40 per hour for her normal daytime work, $9.20 per hour for night work, and $11.75 per hour for holiday work. If her total gross wages for the week were $452.20 and the number of regular daytime hours she worked exceeded the combined hours of night and holiday work by 9 hours, how many hours of each category of work did Amy perform?

  8. Components of a product. A manufacturer buys three components—A, B, and C—for use in making a toaster. She used as many units of A as she did of B and C combined. The cost of A, B, and C is $4, $5, and $6 per unit, respectively. If she purchased 100 units of these components for a total of $480, how many units of each did she purchase?

In Exercises 55–58, use Table 5.1 and Figure 5.8 to determine which grid cells of the patients contain healthy tissue, tumorous tissue, bone, or metal.

Beam decrease, in LAUs
Patient Beam 1 Beam 2 Beam 3

  1. Vicky

 0.54 0.40 0.52

  1. Yolanda

 0.65 0.80 0.75

  1. Nina

 0.51 0.49 0.44

  1. Srinivasan

 0.44 2.21 2.23

Beyond the Basics

In Exercises 59–62, write a linear equation of the form x+by+cz=d that is satisfied by all three of the given ordered triples.

  1. (1, 0, 0), (0, 1, 0), (0, 0, 1)

  2. (13, 0, 0), (0, 4, 3), (1, 2, 2)

  3. (3, −4, 0), (0, 14, 12), (1, 1, −4)

  4. (0, 1, −10), (18, 0, 14), (1, 13, −2)

In Exercises 63–66, find an equation of the parabola of the form y=ax2+bx+c that passes through the three given points.

  1. (0, 1), (−1, 0), (1, 4)

  2. (0, 2), (−1, 30), (2, 6)

  3. (1, 2), (−1, 4), (2, 4)

  4. (0, 3), (−1, 4), (1, 6)

In Exercises 67–70, find an equation of the circle of the form x2+y2+ax+by+c=0 that passes through the three given points.

  1. (0, 4), (2√2, 2√2), (−4, 0)

  2. (0, 3), (0, −1), (√3, 2)

  3. (1, 2), (6, −3), (4, 1)

  4. (5, 6), (−1, 6), (3, 2)

In Exercises 71 and 72, solve the system of equations.

  1. {1x+3y−1z=52x+4y+6z=42x+3y+1z=3

  2. {1x+2y+3z=82x+5y+9z=163x−4y−5z=32

    [Hint: Let 1x=u, 1y=v, and 1z=w. Solve for u, v, and w.]

In Exercises 73 and 74, find the value of c for which the given system has a unique solution.

  1. {x+2y−5z−9=03x−y+2z−14=02x+3y−z−3=0cx−5y+z+3=0

  2. {x+5y+z=423x+y−3z=cx−y+3z=4x+y−z=0

  3. Find a quadratic function of the form y=ax2+bx+c whose graph passes through the points (−1, −1), (0, 5), and (2, 5).

  4. Use Table 5.1 to investigate four grid cells, arranged in a square, as shown in the given figure. Figures (a) and (b) reprinted with permission from Mathematics Teacher, May 1996. © 1996 by National Council of Teachers of Mathematics. All rights reserved.

    1. For Figure (a), the following data were observed.

      1. Beam 1 decreased by 0.60 unit.

      2. Beam 2 decreased by 0.75 unit.

      3. Beam 3 decreased by 0.65 unit.

      4. Beam 4 decreased by 0.70 unit.

      Is there sufficient information in Figure (a) to determine which grid cells may contain tumorous tissue?

    2. From two additional X-rays, as shown in Figure (b), the following data were observed.

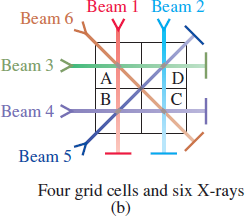
      1. Beam 5 decreased by 0.85 unit.

      2. Beam 6 decreased by 0.50 unit.

      Show that the six X-rays represented in the two figures are sufficient to locate tumors in this situation but that, in fact, it is not necessary to use all six rays.

Critical Thinking / Discussion / Writing

  1. Write a linear system of three equations in the variables x, y, and z that has {(1, −1, 2)} as its solution set.

  2. Write a linear system of three equations in the variables x, y, and z such that

    1. the system has no solution.

    2. the system has infinitely many solutions.

Getting Ready for the Next Section

In Exercises 79–82, solve each equation for the specified variable.

  1. 12⋅3=12+B3, for B

  2. 25⋅7=A5−17, for A

  3. 1n⋅(n+1)=An−1n+1, for A

  4. 4n⋅(n+2)=2n+Bn+2, for B

  5. Find the values of A and B for which the equation

    2x+3=A(x+3)+B(x−1)

    is an identity (true for all values of x). [Hint: Evaluate both sides at x=1 and x=−3.]

  6. Find the values of A and B for which the equation

    3x+2=A(x−2)+B(x+2)

    is an identity

In Exercises 85–90, factor each expression.

  1. x2+5x+6

  2. x2−3x−10

  3. 2x2+5x−3

  4. 3x2+x−2

  5. 4x2−9

  6. x3−8

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.137.41.205