Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Section 8.1 Sequences and Series

Before Starting this Section, Review

1 Algebraic expressions (Section P.1 , page 14)
2 Finding functional values (Section 2.4 , page 219)
3 Graphs of functions (Section 2.4 , page 222)

Objectives

1 Use sequence notation and find specific and general terms in a sequence.
2 Use factorial notation.
3 Use summation notation to write partial sums of a series.

The Family Tree of the Honeybee

The bee that most of us know best is the honeybee, an insect that lives in a colony and has an unusual family tree. Perhaps the most surprising fact about honeybees is that not all of them have two parents. This phenomenon begins with a special female in the colony called the queen. Many other female bees, called worker bees, live in the colony, but unlike the queen bee, they produce no eggs. Male bees do no work and are produced from the queen’s unfertilized eggs. The female bees are produced as a result of the queen bee mating with a male bee. Consequently, all female bees have two parents—a male and a female—whereas male bees have just one parent—a female. In this section, we study sequences, and in Example 5, we see how a famous sequence accurately counts a honeybee’s ancestors.

Sequences

1 Use sequence notation and find specific and general terms in a sequence.

The word sequence is used in mathematics in much the same way it is used in ordinary English. If someone saw a sequence of bad movies, you know that the person could list the first bad movie he or she saw, the second bad movie, and so on.

In computer science, finite sequences of the form $a_{1}, a_{2}, \dots, a_{n}$ are called strings. Sometimes for convenience, we include 0 in the domain of the function that defines a sequence, and we write the sequence terms as $a_{0}, a_{1}, a_{2}, a_{3}, \dots .$ The nth term of such a sequence is $a_{n - 1} .$

We can use subscripts on variables other than a to represent the terms of a sequence. In Example 1(c), we use the variable b.

Example 1 Writing the Terms of a Sequence from the General Term

Write the first four terms of each sequence.

$a_{n} = 5 n - 1$
$a_{n} = \frac{1}{n + 1}$
$b_{n} = {(- 1)}^{n + 1} (\frac{1}{n})$

Solution

The first four terms of each sequence are found by replacing n with the integers 1, 2, 3, and 4 in the equation defining $a_{n} .$

$\begin{array}{rcll} a_{n} & = & 5 n - 1 & General term of the sequence \\ a_{1} & = & 5 (1) - 1 = 4 & 1 st term: Replace n with 1 . \\ a_{2} & = & 5 (2) - 1 = 9 & 2 nd term: Replace n with 2 . \\ a_{3} & = & 5 (3) - 1 = 14 & 3 rd term: Replace n with 3 . \\ a_{4} & = & 5 (4) - 1 = 19 & 4 th term: Replace n with 4 . \end{array}$

The first four terms of the sequence are 4, 9, 14, and 19.
$\begin{array}{rcl} a_{n} & = & \frac{1}{n + 1} \\ a_{1} & = & \frac{1}{1 + 1} = \frac{1}{2} \\ a_{2} & = & \frac{1}{2 + 1} = \frac{1}{3} \\ a_{3} & = & \frac{1}{3 + 1} = \frac{1}{4} \\ a_{4} & = & \frac{1}{4 + 1} = \frac{1}{5} \end{array}$

The first four terms are $\frac{1}{2}, \frac{1}{3}, \frac{1}{4},$ and $\frac{1}{5} .$
$\begin{array}{rcl} b_{n} & = & {(- 1)}^{n + 1} (\frac{1}{n}) \\ b_{1} & = & {(- 1)}^{1 + 1} (\frac{1}{1}) = {(- 1)}^{2} (1) = 1 \\ b_{2} & = & {(- 1)}^{2 + 1} (\frac{1}{2}) = {(- 1)}^{3} (\frac{1}{2}) = - \frac{1}{2} \\ b_{3} & = & {(- 1)}^{3 + 1} (\frac{1}{3}) = {(- 1)}^{4} (\frac{1}{3}) = \frac{1}{3} \\ b_{4} & = & {(- 1)}^{4 + 1} (\frac{1}{4}) = {(- 1)}^{5} (\frac{1}{4}) = - \frac{1}{4} \end{array}$

The first four terms are $1, - \frac{1}{2}, \frac{1}{3},$ and $- \frac{1}{4} .$

Practice Problem 1

Write the first four terms of the sequence with general term $a_{n} = - 2^{n} .$

We can visualize a sequence and study its behavior by plotting its terms as ordered pairs $(n, a_{n})$ in the Cartesian plane. The points representing the graph of the sequence, given by its general term $a_{n} = f (n)$ , will lie on the graph of the corresponding function $y = f (x), x > 0$ . We can use this fact to better understand the patterns in the given sequence. However, not every sequence will have a concise and simple formula for its general term.

Example 2 Graphing a Sequence Given by Its General Term

Graph the first four terms of each sequence and the corresponding function on the Cartesian plane.

$a_{n} = \frac{1}{2} n + 1$
$b_{n} = n^{2} - 3 n$

Solution

To graph this sequence, we need to plot the points $(n, \frac{1}{2} n + 1)$ for $n = 1, 2, 3, \dots .$ The first four points are

$(1, \frac{3}{2}), (2, 2), (3, \frac{5}{2}), (4, 3), \dots$

as shown in Figure 8.1(a). Notice that the graph of this sequence lies on the graph of the linear function $f (x) = \frac{1}{2} x + 1 .$ (see Figure 8.1(b).) If we remove all the points on the graph of $y = \frac{1}{2} x + 1,$ except those whose x-coordinates are positive integers, we get the graph of our sequence.

Figure 8.1
To graph the sequence $b_{n} = n^{2} - 3 n$ , we need to plot the points $(n, n^{2} - 3 n)$ for $n = 1, 2, 3, \dots .$ The first four points are

$(1, - 2), (2, - 2), (3, 0), (4, 4), \dots$

as shown in Figure 8.2(a). The graph of the corresponding quadratic function $f (x) = x^{2} - 3 x$ , is shown in Figure 8.2(b).

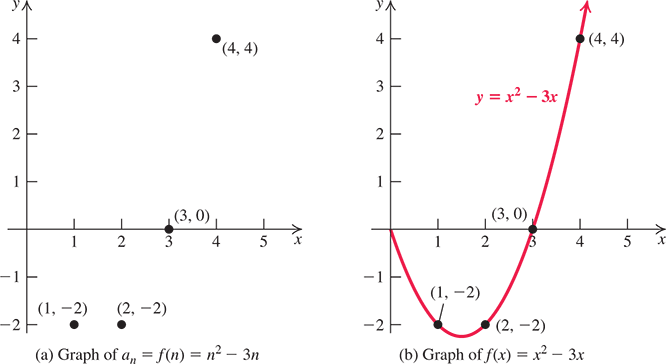
Figure 8.2

Practice Problem 2

Repeat Example 2 for the sequence $a_{n} = 1 + {(\frac{1}{2})}^{n} .$

Observe that there are many different ways of connecting the points that form the graph of a sequence. This means that the same sequence may be produced by general term formulas that correspond to different functions, $y = f (x), x > 0$ (we explore this further in Exercise 127). The skill is to choose the function that best mirrors the behavior of the given sequence. Frequently, the first few terms of a sequence exhibit a pattern that suggests a natural choice for the general term of the sequence.

Example 3 Finding a General Term of a Sequence from a Pattern

Write the general term $a_{n}$ for a sequence whose first five terms are given.

1, 4, 9, 16, 25, …
$0, \frac{1}{2}, - \frac{2}{3}, \frac{3}{4}, - \frac{4}{5}, \dots$

Solution

Write the position number of the term above each term of the sequence and look for a pattern that connects the term to the position number of the term.

$\begin{array}{l} n : & 1, & 2, & 3, & 4, & 5, & \dots, & n \\ term : & 1, & 4, & 9, & 16, & 25, & \dots, & a_{n} \end{array}$

Apparent pattern: Here $1 = 1^{2}, 4 = 2^{2}, 9 = 3^{2}, 16 = 4^{2},$ and $25 = 5^{2} .$ Each term is the square of the position number of that term. This suggests $a_{n} = n^{2} .$
$\begin{array}{lllrlrll} n : & 1, & 2, & 3, & 4, & 5, & \dots, & n \\ term : & 0, & \frac{1}{2}, & - \frac{2}{3}, & \frac{3}{4}, & - \frac{4}{5}, & \dots, & a_{n} \end{array}$

Apparent pattern: When the terms alternate in sign and $n = 1,$ we use the factor ${(- 1)}^{n}$ if we want to begin with the factor $- 1$ , and we use the factor ${(- 1)}^{n + 1}$ if we want to begin with the factor 1. Notice that each term can be written as a quotient with denominator equal to the position number and numerator equal to one less than the position number, suggesting the general term $a_{n} = {(- 1)}^{n} \frac{n - 1}{n} .$

Practice Problem 3

Write a general term for a sequence whose first five terms are $0, - \frac{1}{2}, \frac{2}{3}, - \frac{3}{4}, \frac{4}{5}, \dots .$

Warning

In Example 3, we found the general term of a sequence by finding a pattern in the first few terms of the sequence. However, when only a finite number of successive terms are given without a rule that defines the general term, a unique general term cannot be found.

To indicate why this is so, consider the two sequences:

$\begin{array}{rcl} a_{n} & = & n^{2}, and \\ b_{n} & = & n^{2} + (n - 1) (n - 2) (n - 3) (n - 4) . \end{array}$

The first four terms of these two sequences are identical: 1, 4, 9, 16. However, the fifth term is different: $a_{5} = 25,$ but $b_{5} = 49 .$ Thus, either $a_{n}$ or $b_{n}$ could correctly describe a sequence whose first four terms are 1, 4, 9, and 16. You can never find a unique general term from a finite number of terms in a sequence.

Recursive Formulas

Up to this point, we have expressed the general term as a function of the position of the term in the sequence. A second approach is to define a sequence recursively. A recursive formula requires that one or more of the first few terms of the sequence be specified and all other terms be defined in relation to previously defined terms.

For example, the Fibonacci sequence is a famous sequence that is defined recursively and occurs often in nature. In this sequence, we specify the first two terms as $a_{0} = 1$ and $a_{1} = 1;$ each subsequent term is the sum of the two terms immediately preceding it. So we have

$\begin{array}{l} a_{0} = 1, a_{1} = 1, a_{2} = a_{0} + a_{1} = 1 + 1 = 2 & Add the two given terms . \\ a_{1} = 1, a_{2} = 2, a_{3} = a_{1} + a_{2} = 1 + 2 = 3 & Add the two previous terms . \\ a_{2} = 2, a_{3} = 3, a_{4} = a_{2} + a_{3} = 2 + 3 = 5 & Add the two previous terms . \\ a_{3} = 3, a_{4} = 5, a_{5} = a_{3} + a_{4} = 3 + 5 = 8 & Add the two previous terms . \end{array}$

The first six terms of the sequence are

$1, 1, 2, 3, 5, 8 .$

This sequence can also be defined in subscript notation:

$a_{0} = 1, a_{1} = 1, a_{k} = a_{k - 2} + a_{k - 1}, for all integers k \geq 2 .$

Replacing k with 2, 3, 4, and 5, respectively, in the equation $a_{k} = a_{k - 2} + a_{k - 1}$ will produce the values $a_{2} = 2, a_{3} = 3, a_{4} = 5,$ and $a_{5} = 8 .$

Example 4 Finding Terms of a Recursively Defined Sequence

Write the first five terms of the recursively defined sequence

$a_{1} = 4, a_{n + 1} = 2 a_{n} - 9 .$

Solution

We are given the first term of the sequence: $a_{1} = 4 .$

$\begin{array}{rcll} a_{2} & = & 2 a_{1} - 9 & Replace n with 1 in a_{n + 1} = 2 a_{n} - 9 . \\ a_{2} & = & 2 (4) - 9 = - 1 & Replace a_{1} with 4 . \\ a_{3} & = & 2 a_{2} - 9 & Replace n with 2 in a_{n + 1} = 2 a_{n} - 9 . \\ a_{3} & = & 2 (- 1) - 9 = - 11 & Replace a_{2} with - 1 . \\ a_{4} & = & 2 a_{3} - 9 & Replace n with 3 in a_{n + 1} = 2 a_{n} - 9 . \\ a_{4} & = & 2 (- 11) - 9 = - 31 & Replace a_{3} with - 11 . \\ a_{5} & = & 2 a_{4} - 9 & Replace n with 4 in a_{n + 1} = 2 a_{n} - 9 . \\ a_{5} & = & 2 (- 31) - 9 = - 71 & Replace a_{4} with - 31 . \end{array}$

Thus, the first five terms of the sequence are

$4, - 1, - 11, - 31, - 71 .$

Practice Problem 4

Write the first five terms of the recursively defined sequence $a_{1} = - 3, a_{n + 1} = 2 a_{n} + 5 .$

Example 5 Diagramming the Family Tree of a Honeybee

Find a sequence that accurately counts the ancestors of a male honeybee. The first term of the sequence should give the number of parents of a male honeybee, the second term the number of grandparents, the third term the number of great-grandparents, and so on.

Solution

Recall from the introduction to this section that female honeybees have two parents—a male and a female—but that male honeybees have just one parent—a female.

Consider the family tree of a male honeybee. A male bee has one parent: a female. Because his mother had two parents, he has two grandparents. Because his grandmother had two parents and his grandfather had only one parent, he has three great-grandparents.

Now to count the bee’s ancestors, we count backward using Figure 8.3. You should recognize the first six terms of the Fibonacci sequence: 1, 1, 2, 3, 5, 8. This sequence is defined by $a_{0} = 1, a_{1} = 1,$ and $a_{k} = a_{k - 2} + a_{k - 1},$ for all $k \geq 2 .$

Practice Problem 5

Find a sequence that accurately counts the ancestors of a female honeybee.

Factorial Notation

2 Use factorial notation.

Special types of products, called factorials, appear in some very important sequences.

Here are the first eight values of n!

$\begin{array}{l} 0! = 1 & 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 \\ 1! = 1 & 5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 \\ 2! = 2 \cdot 1 = 2 & 6! = 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720 \\ 3! = 3 \cdot 2 \cdot 1 = 6 & 7! = 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 5040 \end{array}$

The values of n! get large very quickly. For example, $10! = 3,628,800$ and $12! = 479,001,600 .$

In simplifying some expressions involving factorials, it is helpful to note that

$n! = n \cdot (n - 1)!$

Example 6 Simplifying a Factorial Expression

Simplify.

$\frac{16!}{14!}$
$\frac{(n + 1)!}{(n - 1)!}$

Solution

$\begin{array}{rcll} \frac{16!}{14!} & = & \frac{16 \cdot 15 \cdot 14!}{14!} & 16! = 16 \cdot 15! = 16 \cdot 15 \cdot 14! \\ = & 16 \cdot 15 = 240 & Divide out the factor 14! \end{array}$
$\begin{array}{rcll} \frac{(n + 1)!}{(n - 1)!} & = & \frac{(n + 1) \cdot n \cdot (n - 1)!}{(n - 1)!} & \begin{array}{l} (n + 1)! = (n + 1) \cdot n! = \\ (n + 1) \cdot n \cdot (n - 1)! \end{array} \\ = & (n + 1) n & Divide out the common factor (n - 1)! \end{array}$

Practice Problem 6

Simplify.
1. $\frac{13!}{12!}$
2. $\frac{n!}{(n - 3)!}$

Example 7 Writing Terms of a Sequence Involving Factorials

Write the first five terms of the sequence whose general term is $a_{n} = \frac{{(- 1)}^{n + 1}}{n!} .$

Solution

Replace n in the formula for the general term with each positive integer from 1 through 5.

$\begin{array}{l} a_{1} = \frac{{(- 1)}^{1 + 1}}{1!} = \frac{{(- 1)}^{2}}{1} = 1 & a_{4} = \frac{{(- 1)}^{4 + 1}}{4!} = \frac{{(- 1)}^{5}}{24} = - \frac{1}{24} \\ a_{2} = \frac{{(- 1)}^{2 + 1}}{2!} = \frac{{(- 1)}^{3}}{2} = - \frac{1}{2} & a_{5} = \frac{{(- 1)}^{5 + 1}}{5!} = \frac{{(- 1)}^{6}}{120} = \frac{1}{120} \\ a_{3} = \frac{{(- 1)}^{3 + 1}}{3!} = \frac{{(- 1)}^{4}}{6} = \frac{1}{6} \end{array}$

Using these five terms, we could write this sequence as

$1, - \frac{1}{2}, \frac{1}{6}, - \frac{1}{24}, \frac{1}{120}, \dots .$

Practice Problem 7

Write the first five terms of the sequence whose general term is

$a_{n} = \frac{{(- 1)}^{n} 2^{n}}{n!} .$

Summation Notation

3 Use summation notation to write partial sums of a series.

If we know the general term of a sequence, we can represent a sum of terms of the sequence by using summation (or sigma) notation. In this notation, the Greek letter $\sum$ (capital sigma) indicates that we are to add the given terms. The letter $\sum$ corresponds to the English letter S, the first letter of the word sum.

In summation notation, the index need not start at $i = 1 .$ Also, any letter may be used in place of the index i. In general, we have

$\sum_{j = k}^{n} a_{j} = a_{k} + a_{k + 1} + \dots + a_{n}, n \geq k \geq 0 .$

Example 8 Evaluating Sums Given in Summation Notation

Find each sum.

$\sum_{i = 1}^{9} i$
$\sum_{j = 4}^{7} (2 j^{2} - 1)$
$\sum_{k = 0}^{4} \frac{2^{k}}{k!}$

Solution

Replace i with successive integers from 1 to 9 inclusive; then add.

$\sum_{i = 1}^{9} i = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45$
The index of summation is j. Evaluate $(2 j^{2} - 1)$ for all consecutive integers from 4 through 7 inclusive; then add.

$\begin{array}{rcl} \sum_{j = 4}^{7} (2 j^{2} - 1) & = & [2 {(4)}^{2} - 1] + [2 {(5)}^{2} - 1] + [2 {(6)}^{2} - 1] + [2 {(7)}^{2} - 1] \\ = & 31 + 49 + 71 + 97 = 248 \end{array}$
The index of summation is k. Evaluate $\frac{2^{k}}{k!}$ for consecutive integers 0 through 4 inclusive; then add.

$\begin{array}{rcl} \sum_{k = 0}^{4} \frac{2^{k}}{k!} & = & \frac{2^{0}}{0!} + \frac{2^{1}}{1!} + \frac{2^{2}}{2!} + \frac{2^{3}}{3!} + \frac{2^{4}}{4!} \\ = & \frac{1}{1} + \frac{2}{1} + \frac{4}{2} + \frac{8}{6} + \frac{16}{24} = 1 + 2 + 2 + \frac{4}{3} + \frac{2}{3} = 7 \end{array}$

Practice Problem 8

Find the following sum: $\sum_{k = 0}^{3} {(- 1)}^{k} k!$

The familiar properties of real numbers, such as the distributive, commutative, and associative properties, can be used to prove the summation properties listed next.

Series

We all know how to add numbers, but do you think it is possible to add infinitely many numbers? It is sometimes possible to add infinitely many numbers, although a complete explanation of this kind of addition must be put off until a calculus course. For now, we need some definitions.

Example 9 Writing a Sum in Summation Notation

Write each sum in summation notation.

$3 + 5 + 7 + \dots + 21$
$\frac{1}{4} + \frac{1}{9} + \dots + \frac{1}{49}$

Solution

The finite series $3 + 5 + 7 + \dots + 21$ is a sum of consecutive odd numbers from 3 to 21. Each of these numbers can be expressed in the form $2 k + 1,$ starting with $k = 1$ and ending with $k = 10 .$ With k as the index of summation, 1 as the lower limit, and 10 as the upper limit, we write

$3 + 5 + 7 + \dots + 21 = \sum_{k = 1}^{10} (2 k + 1) .$
The finite series $\frac{1}{4} + \frac{1}{9} + \dots + \frac{1}{49}$ is a sum of fractions, each of which has numerator 1 and denominator $k^{2},$ starting with $k = 2$ and ending with $k = 7 .$ We write

$\frac{1}{4} + \frac{1}{9} + \dots + \frac{1}{49} = \sum_{k = 2}^{7} \frac{1}{k^{2}} .$

Practice Problem 9

Write the following in summation notation: $2 - 4 + 6 - 8 + 10 - 12 + 14$

Section 8.1 Exercises

Concepts and Vocabulary

An infinite sequence is a function whose domain is the set of .
If a sequence is defined by $a_{n} = 2 n - \frac{10}{n},$ then $a_{5} = \underline{}$ .
By definition, $0! = \underline{}$ .
The notation $\sum_{k = 1}^{5} k^{2} = 1^{2} + 2^{2} + 3^{2} + 4^{2} + 5^{2}$ is an example of notation.
True or False. If $a_{1} = 3$ and $a_{n + 1} = a_{n}^{2},$ then $a_{3} = 27 .$
True or False. $\frac{(2 n)!}{n!} = 2 .$
True or False. $\sum_{k = 0}^{5} \frac{2 k + 1}{2} = 18$
True or False. $(2 n + 1)! = (2 n + 1) \cdot (2 n)!$

Building Skills

In Exercises 9–28, write the first four terms of each sequence.

$a_{n} = 3 n - 2$
$a_{n} = 2 n + 1$
$a_{n} = 1 - \frac{1}{n}$
$a_{n} = 1 + \frac{1}{n}$
$a_{n} = - n^{2}$
$a_{n} = n^{3}$
$a_{n} = \frac{2 n}{n + 1}$
$a_{n} = \frac{3 n}{n^{2} + 1}$
$a_{n} = {(- 1)}^{n + 1}$
$a_{n} = {(- 3)}^{n - 1}$
$a_{n} = 3 - \frac{1}{2^{n}}$
$a_{n} = {(\frac{3}{2})}^{n}$
$a_{n} = 0.6$
$a_{n} = - 0.4$
$a_{n} = \frac{{(- 1)}^{n}}{n!}$
$a_{n} = \frac{n}{n!}$
$a_{n} = {(- 1)}^{n} 3^{- n}$
$a_{n} = {(- 1)}^{n} 3^{n - 1}$
$a_{n} = \frac{e^{n}}{2 n}$
$a_{n} = \frac{2^{n}}{e^{n}}$

In Exercises 29–38, graph the first four terms of each sequence and the corresponding function (or functions) on the Cartesian plane.

$a_{n} = 2 n - 3$
$a_{n} = 2 - n$
$a_{n} = \frac{1}{2} n^{2} - n$
$a_{n} = 4 - \frac{1}{2} n^{2}$
$a_{n} = {(n - 2)}^{2} - 1$
$a_{n} = - {(n - 1)}^{2} + 2$
$a_{n} = 3 - \frac{1}{n}$
$a_{n} = 2 + \frac{1}{n}$
$a_{n} = 2^{n - 1} - 3$
$a_{n} = 3 - 2^{n - 1}$

In Exercises 39–52, write a general term $a_{n}$ for each sequence. Assume that n begins with 1.

1, 4, 7, 10, …
7, 9, 11, 13, …
$\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \dots$
$\frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \dots$
$2, - 2, 2, - 2, \dots$
$- 3, 6, - 9, 12, \dots$
$\frac{1}{2}, \frac{3}{4}, \frac{9}{8}, \frac{27}{16}, \dots$
$- \frac{1}{2}, \frac{1}{4}, - \frac{1}{8}, \frac{1}{16}, \dots$
$1 \cdot 2, 2 \cdot 3, 3 \cdot 4, 4 \cdot 5, \dots$
$- \frac{1}{1 \cdot 2}, \frac{1}{2 \cdot 3}, - \frac{1}{3 \cdot 4}, \frac{1}{4 \cdot 5}, \dots$
$2 + \frac{1}{2}, 2 - \frac{1}{3}, 2 + \frac{1}{4}, 2 - \frac{1}{5}, \dots$
$1 + \frac{1}{2}, 1 + \frac{1}{3}, 1 + \frac{1}{4}, 1 + \frac{1}{5}, \dots$
$\frac{3^{2}}{2}, \frac{3^{3}}{3}, \frac{3^{4}}{4}, \frac{3^{5}}{5}, \dots$
$\frac{e}{2}, \frac{e^{2}}{4}, \frac{e^{3}}{8}, \frac{e^{4}}{16}, \dots$

In Exercises 53–62, write the first five terms of each recursively defined sequence.

$a_{1} = 2, a_{n + 1} = a_{n} + 3$
$a_{1} = 5, a_{n + 1} = a_{n} - 1$
$a_{1} = 3, a_{n + 1} = 2 a_{n}$
$a_{1} = 1, a_{n + 1} = \frac{1}{2} a_{n}$
$a_{1} = 7, a_{n + 1} = - 2 a_{n} + 3$
$a_{1} = - 4, a_{n + 1} = - 3 a_{n} - 5$
$a_{1} = 2, a_{n + 1} = \frac{1}{a_{n}}$
$a_{1} = - 1, a_{n + 1} = \frac{- 1}{a_{n}}$
$a_{1} = 25, a_{n + 1} = \frac{{(- 1)}^{n}}{5 a_{n}}$
$a_{1} = 12, a_{n + 1} = \frac{{(- 1)}^{n}}{3 a_{n}}$

In Exercises 63–68, use a graphing calculator to (a) find the first 10 terms of the sequence and (b) graph the first 10 terms of the sequence.

$a_{n} = 3 n^{2} - 1$
$a_{n} = 4 - \frac{3}{n}$
$a_{n} = n (1 - \frac{1}{n})$
$a_{n} = n^{3} - n^{2}$
$a_{n} = 1 - \frac{1}{a_{n - 1}}, a_{1} = \frac{1}{2}$
$a_{n} = a_{n - 1}^{2}, a_{1} = 1$

In Exercises 69–76, simplify the factorial expression.

$\frac{3!}{5!}$
$\frac{8!}{10!}$
$\frac{12!}{11!}$
$\frac{20!}{18!}$
$\frac{n!}{(n + 1)!}$
$\frac{(n - 1)!}{(n - 2)!}$
$\frac{(2 n + 1)!}{(2 n)!}$
$\frac{(2 n + 1)!}{(2 n - 1)!}$

In Exercises 77–88, find each sum.

$\sum_{k = 1}^{7} 5$
$\sum_{j = 1}^{4} 12$
$\sum_{j = 0}^{5} j^{2}$
$\sum_{k = 0}^{4} k^{3}$
$\sum_{i = 1}^{5} (2 i - 1)$
$\sum_{k = 0}^{6} (1 - 3 k)$
$\sum_{j = 3}^{7} \frac{j + 1}{j}$
$\sum_{k = 3}^{8} \frac{1}{k + 1}$
$\sum_{i = 2}^{6} {(- 1)}^{i} 3^{i - 1}$
$\sum_{k = 2}^{4} {(- 1)}^{k + 1} k$
$\sum_{k = 4}^{7} (2 - k^{2})$
$\sum_{j = 4}^{9} (_{} j^{3} + 1)$

In Exercises 89–96, write each sum in summation notation.

$1 + 3 + 5 + 7 + \dots + 101$
$2 + 4 + 6 + 8 + \dots + 102$
$\frac{1}{5 (1)} + \frac{1}{5 (2)} + \frac{1}{5 (3)} + \frac{1}{5 (4)} + \dots + \frac{1}{5 (11)}$
$\frac{2}{1 \cdot 2} + \frac{2}{2 \cdot 3} + \frac{2}{3 \cdot 4} + \frac{2}{4 \cdot 5} + \dots + \frac{2}{9 \cdot 10}$
$1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \dots - \frac{1}{50}$
$1 - 2 + 3 - 4 + \dots + (- 50)$
$\frac{1}{2} + \frac{2}{3} + \frac{3}{4} + \frac{4}{5} + \dots + \frac{10}{11}$
$\frac{2}{1} + \frac{2^{2}}{2} + \frac{2^{3}}{3} + \frac{2^{4}}{4} + \dots + \frac{2^{10}}{10}$

In Exercises 97–102, use a graphing calculator to find each sum.

$\sum_{i = 1}^{10} 12 i^{2}$
$\sum_{i = 1}^{50} (2 i + 7)$
$\sum_{k = 5}^{30} \frac{7}{1 - k^{2}}$
$\sum_{k = 10}^{25} \frac{{(k + 1)}^{2}}{k}$
$\sum_{j = 1}^{100} {(- 1)}^{j} j$
$\sum_{j = 8}^{50} (7 + \frac{{(- 1)}^{j}}{j})$

Applying the Concepts

Free fall. In the absence of friction, a freely falling body will fall about 16 feet the first second, 48 feet the next second, 80 feet the third second, 112 feet the fourth second, and so on. How far has it fallen during
1. The seventh second?
2. The nth second?
Bacterial growth. A colony of 1000 bacteria doubles in size every hour. How many bacteria will there be in
1. 2 hours?
2. 5 hours?
3. n hours?
Workplace fines. A contractor who quits work on a house was told she would be fined $50 if she did not resume work on Monday, $75 if she failed to resume work on Tuesday, $100 if she did not resume work on Wednesday, and so on (including weekends). How much will her fine be on the ninth day she fails to show up for work?
Appreciating value. A painting valued at $30,000 is expected to appreciate $1280 the first year, $1240 the second year, $1200 the third year, and so on. How much will the painting appreciate in
1. The seventh year?
2. The tenth year?
Cell phone use. At the end of the first six months after a company began providing cell phones to its sales force, it averaged 600 cell minutes per month. For the next four years, its monthly cell phone use doubled every six months. How many cell minutes per month were being used at the end of three years?
Motorcycle acceleration. A motorcycle travels 10 yards the first second and then increases its speed by 20 yards per second in each succeeding second. At this rate, how far will the motorcycle travel during
1. The eighth second?
2. The nth second?
Compound interest. Suppose $10,000 is deposited into an account that earns 6% interest compounded semiannually. The balance in the account after n compounding periods is given by the sequence

$A_{n} = 10,000 {(1 + \frac{0.06}{2})}^{n}, n = 1, 2, 3, \dots .$
1. Find the first six terms of this sequence.
2. Find the balance in the account after 8 years.
Compound interest. Suppose $100 is deposited at the beginning of a year into an account that earns 8% interest compounded quarterly. The balance in the account after n compounding periods is

$A_{n} = 100 {(1 + \frac{0.08}{4})}^{n}, n = 1, 2, 3, \dots .$
1. Find the first six terms of this sequence.
2. Find the balance in the account after ten years.
Real estate value. Analysts estimate that a $100,000 condominium will increase 5% in value each year for the next seven years. Find the value of the condominium in each of those years. Write a formula for a sequence whose first seven terms give these values.
Diminishing savings. Laura withdraws 10% of her $50,000 savings each year. Find the amount remaining in her account for each of the next ten years. Write a formula for a sequence whose first ten terms give these values.

Beyond the Basics

Find a formula for the nth term of the sequence defined recursively by $a_{1} = \sqrt{2}, a_{n + 1} = \sqrt{2 a_{n}} .$ [Hint: Write each of the first five terms as a power of 2.]
The triangular tiles used in the figures shown have white interiors and gold edges. A sequence of figures is obtained by adding one triangle to the previous figure.
1. Write a recursive sequence whose nth term, $a_{n},$ gives the number of gold edges in the nth figure.
2. Write a recursive sequence whose nth term, $b_{n},$ gives the number of gold edges that lie on the perimeter of the nth figure.
The figure shows a sequence of successively smaller squares formed by connecting the midpoints of the sides of the preceding larger square. The area of the largest square is 1.
1. Write the first five terms of the sequence whose general term, $a_{n},$ gives the area of the nth square.
2. Write the general term, $a_{n},$ of the sequence.
A sequence of concentric circles is designed so that the radius of the first circle is 1 and each successive circle has a radius that is twice the length of the radius of the preceding circle. Write a recursive sequence whose nth term, $a_{n},$ gives the area of the nth circle.
Find the first ten terms of the sequence defined recursively by $a_{1} = a_{2} = 1, a_{n} = a_{a_{n - 1}} + a_{n - a_{n - 1}} .$ In 1989, a prize of $1000 was offered to whoever first discovered (for this sequence) a value of n for which $| \frac{a_{i}}{i} | - | \frac{1}{2} | < \frac{1}{20}$ for all $i > n .$ A mathematician named Colin L. Mallows of AT&T/Bell Laboratories found that $n = 1489$ and claimed the prize.

(Source: http://el.media.mit.edu/logo-foundation/pubs/papers/easy_as_11223.html)
A sequence of numbers $a_{0}, a_{1}, a_{2}, a_{3}, \dots$ satisfies the equation

$a_{n}^{2} = {(- 1)}^{n} a_{n - 1} + a_{n + 1} .$

If $a_{0} = 1$ and $a_{1} = 3,$ find $a_{3} .$
Find a sequence with general term $a_{m}$ such that

$\sum_{n = 1}^{20} n^{2} = \sum_{m = 0}^{19} a_{m} .$
Find a real number c such that

$\sum_{n = 1}^{50} {(n - 3)}^{2} = \sum_{n = 1}^{50} (n^{2} - 6 n) + \sum_{n = 1}^{50} c .$
Find a lower limit p and an upper limit q such that

$\sum_{n = 0}^{10} n^{3} = \sum_{m = p}^{q} {(m - 2)}^{3} .$
Give an example of two sequences $a_{k}$ and $b_{k}$ such that

$\sum_{k = 1}^{20} a_{k} b_{k} \neq (\sum_{k = 1}^{20} a_{k}) (\sum_{k = 1}^{20} b_{k}) .$
Show that $7! - 2 (5!) = 40 (5!) .$
Show that $\frac{10!}{6! 4!} + \frac{10!}{5! 5!} = \frac{11!}{6! 5!} .$
If $\frac{1}{5!} + \frac{1}{6!} = \frac{x}{7!},$ find x.
If $(n + 1)! = 12 (n - 1)!,$ find n.

Critical Thinking / Discussion / Writing

A constant sequence can be produced using either of the following general term formulas

$a_{n} = 1, b_{n} = 1 + n - 〚 n 〛 .$

Graph each sequence and the corresponding function for each general term. Discuss which general term formula is a better fit for this sequence.
Graph the sequence

$a_{n} = 1 + \frac{{(- 1)}^{n}}{n} .$

Note that the points representing this sequence alternate between the graphs of two functions. What are these two functions? Identify the number the values of $a_{n}$ approach as $n \to \infty$ .
Find the largest integer value for the upper limit k if

$\begin{array}{l} \sum_{n = 1}^{k} (n^{2} + n) \\ = \sum_{n = 1}^{k}_{} [(n - 1) (n - 2) (n - 3) (n - 4) (n - 5) + n^{2} + n] . \end{array}$
The Ulam conjecture. Define the sequence $a_{n}$ recursively by

$a_{n} = {\begin{array}{l} \frac{a_{n - 1}}{2} & if a_{n - 1} is even \\ 3 a_{n - 1} + 1 & if a_{n - 1} is odd . \end{array}$

The Ulam conjecture says that if your first term $a_{0}$ is any positive integer, the sequence $a_{n}$ will eventually reach the integer 1. Verify the conjecture for $a_{0} = 13 .$
Show that $\frac{(2 n)!}{n!} = [1 \cdot 3 \cdot 5 \cdot \dots (2 n - 1)] 2^{n} .$
Explain why $(n! + 1)$ is not divisible by any integer between 2 and n.

Getting Ready for the Next Section

For each sequence in Exercises 133–136, find $a_{2} - a_{1}, a_{3} - a_{2},$ $a_{4} - a_{3},$ and $a_{5} - a_{4} .$

1, 5, 9, 13, 17,
2, 5.2, 8.4, 11.6, 14.8.
$6, 1, - 4, - 9, - 14$
$5, 1.5, - 2, - 5.5, - 9$

In Exercises 137–140, the first term $a_{1}$ and a number d are given. Write the next four terms of the sequence defined by $a_{2} = a_{1} + d, a_{3} = a_{2} + d, a_{4} = a_{3} + d,$ and $a_{5} = a_{4} + d .$

$a_{1} = 3, d = 4$
$a_{1} = 4, d = 2.5$
$a_{1} = 7, d = - 3$
$a_{1} = 8, d = - 4.5$

In Exercises 141–146, the nth term $a_{n}$ is given. Find $a_{2} - a_{1}, a_{3} - a_{2}, a_{4} - a_{3},$ and $a_{5} - a_{4} .$

$a_{n} = 3 n + 5$
$a_{n} = 5 n - 7$
$a_{n} = - 2 n - 6$
$a_{n} = - 3 n + 8$
Let $a_{n} = 2 n - 5 .$ Find $a_{n + 1}$ and $a_{n - 1} .$
Let $a_{n} = - 3 n + 4 .$ Find $a_{n + 1}$ and $a_{n - 1} .$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Section 8.1 Sequences and Series

Create new playlist

Sign In

Sign Up

Table of Contents for
Section 8.1 Sequences and Series