Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Section P.2 Integer Exponents and Scientific Notation

Before Starting This Section, Review

1 Properties of opposites (Section P.1 , page 13)
2 Variables (Section P.1 , page 2)

Objectives

1 Use integer exponents.
2 Use the rules of exponents.
3 Simplify exponential expressions.
4 Use scientific notation.

Coffee and Candy Consumption in America

In 2012, Americans drank about 110 billion cups of coffee and spent more than $29 billion on candy and other confectionery products. The American population at that time was about 314 million. Because our day-to-day activities bring us into contact with more manageable quantities, most people find large numbers like those just cited a bit difficult to understand. Using exponents, the method of scientific notation allows us to write large and small quantities in a manner that makes comparing such quantities fairly easy. In turn, these comparisons help us get a better perspective on these quantities. In Example 9 of this section, without relying on a calculator, we see that if we distribute the cost of the candy and other confectionery products used in 2012 evenly among all individuals in the United States, each person will spend over $92. Distributing the coffee used in 2012 evenly among all individuals in the United States gives each person about 350 cups of coffee.

Integer Exponents

1 Use integer exponents.

In Section P.1, we introduced the following notation:

If a is a real number and n is a positive integer, then

a n = a \cdot a \cdot \dots \cdot a              n factors .

$a^{n} = \underset{n factors}{\underset{︸}{a \cdot a \cdot \dots \cdot a}} .$

We now define an $a^{n}$ when the exponent is 0 or a negative integer.

Warning

Negative exponents indicate the reciprocal of a number. Zero cannot be used as a base with a negative exponent because zero does not have a reciprocal. Furthermore, 00 $0^{0}$ is not defined. We assume throughout this text that the base is not equal to zero if any of the exponents are negative or zero.

Example 1 Evaluating Expressions That Use Zero or Negative Exponents

Evaluate.

(−5)−2 ${(- 5)}^{- 2}$
−5−2 $- 5^{- 2}$
80 $8^{0}$
(23)−3 ${(\frac{2}{3})}^{- 3}$

Solution

(−5)−2=1(−5)2=125The exponent −2 applies to the base −5. ${(- 5)}^{- 2} = \frac{1}{{(- 5)}^{2}} = \frac{1}{25} The exponent - 2 applies to the base - 5.$
−5−2=−152=−125The exponent −2 applies to the base 5. $- 5^{- 2} = - \frac{1}{5^{2}} = - \frac{1}{25} The exponent - 2 applies to the base 5.$
80=1By definition $8^{0} = 1 By definition$
(23)−3=1(23)3=1827=278(23)3=23⋅23⋅23=827 ${(\frac{2}{3})}^{- 3} = \frac{1}{{(\frac{2}{3})}^{3}} = \frac{1}{\frac{8}{27}} = \frac{27}{8} {(\frac{2}{3})}^{3} = \frac{2}{3} \cdot \frac{2}{3} \cdot \frac{2}{3} = \frac{8}{27}$

Practice Problem 1

Evaluate.
1. 2−1 $2^{- 1}$
2. (45)0 ${(\frac{4}{5})}^{0}$
3. (32)−2 ${(\frac{3}{2})}^{- 2}$

In Example 1, we see that parts a and b give different results. In part a, the base is −5 $- 5$ and the exponent is −2, $- 2,$ whereas in part b, we evaluate the opposite of the expression with base 5 and exponent −2. $- 2 .$

Rules of Exponents

2 Use the rules of exponents.

We now review the rules of exponents.

Let’s see what happens when we multiply a5 $a^{5}$ by a3. $a^{3} .$ We have

a 5 \cdot a 3 = (a \cdot a \cdot a \cdot a \cdot a)                  5 factors \cdot (a \cdot a \cdot a)          3 factors = a \cdot a \cdot a \cdot a \cdot a \cdot a \cdot a \cdot a                          5 + 3 = 8 factors = a 8 .

$a^{5} \cdot a^{3} = \underset{5 factors}{\underset{︸}{(a \cdot a \cdot a \cdot a \cdot a)}} \cdot \underset{3 factors}{\underset{︸}{(a \cdot a \cdot a)}} = \underset{5 + 3 = 8 factors}{\underset{︸}{a \cdot a \cdot a \cdot a \cdot a \cdot a \cdot a \cdot a}} = a^{8} .$

Similarly, if you multiply m factors of a by n factors of a, you get m+n $m + n$ factors of a.

Example 2 Using the Product Rule of Exponents

Simplify. Use the product rule and (if necessary) the definition of a negative exponent or reciprocal to write each answer without negative exponents.

2x3⋅x5 $2 x^{3} \cdot x^{5}$
x7⋅x−7 $x^{7} \cdot x^{- 7}$
(−4y2)(3y7) $(- 4 y^{2}) (3 y^{7})$

Solution

2x3⋅x5=2x3+5=2x8Add exponents: 3+5=8. $2 x^{3} \cdot x^{5} = 2 x^{3 + 5} = 2 x^{8} Add exponents: 3 + 5 = 8.$
x7⋅x−7=x7+(−7)=x0=1Add exponents: 7+(−7)=0; simplify. $x^{7} \cdot x^{- 7} = x^{7 + (- 7)} = x^{0} = 1 Add exponents: 7 + (- 7) = 0; simplify .$
(−4y2)(3y7)===(−4)3y2y7−12y2+7−12y9Group the factors with variable bases.Add exponents.2+7=9 $\begin{array}{rcll} (- 4 y^{2}) (3 y^{7}) & = & (- 4) 3 y^{2} y^{7} & Group the factors with variable bases . \\ = & - 12 y^{2 + 7} & Add exponents . \\ = & - 12 y^{9} & 2 + 7 = 9 \end{array}$

Practice Problem 2

Simplify. Write each answer without using negative exponents.
1. x2⋅3x7 $x^{2} \cdot 3 x^{7}$
2. (22x3)(4x−3) $(2^{2} x^{3}) (4 x^{- 3})$

Look what happens when we divide a5 $a^{5}$ by a3. $a^{3} .$ We have

a 5 a 3 = a \cdot a \cdot a \cdot a \cdot a a \cdot a \cdot a = a \cdot a \cdot a a \cdot a \cdot a \cdot a \cdot a 1 = a \cdot a = a 2 .

$\frac{a^{5}}{a^{3}} = \frac{a \cdot a \cdot a \cdot a \cdot a}{a \cdot a \cdot a} = \frac{a \cdot a \cdot a}{a \cdot a \cdot a} \cdot \frac{a \cdot a}{1} = a \cdot a = a^{2} .$

So a5a3=a5⋅1a3=a5⋅a−3=a5−3=a2. $\frac{a^{5}}{a^{3}} = a^{5} \cdot \frac{1}{a^{3}} = a^{5} \cdot a^{- 3} = a^{5 - 3} = a^{2} .$ You subtract exponents because the three factors in the denominator cancel three of the factors in the numerator.

Side Note

Remember that if a≠0, $a \neq 0,$ then a0=1; $a^{0} = 1;$ so it is okay for a denominator to contain a nonzero base with a zero exponent. For example,

3 5 0 = 3 1 = 3 .

$\frac{3}{5^{0}} = \frac{3}{1} = 3 .$

Example 3 Using the Quotient Rule of Exponents

Simplify. Use the quotient rule to write each answer without negative exponents.

510510 $\frac{5^{10}}{5^{10}}$
2−123 $\frac{2^{- 1}}{2^{3}}$
x−3x5 $\frac{x^{- 3}}{x^{5}}$

Solution

510510=510−10=50=1 $\frac{5^{10}}{5^{10}} = 5^{10 - 10} = 5^{0} = 1$
2−123=2−1−3=2−4=124=116 $\frac{2^{- 1}}{2^{3}} = 2^{- 1 - 3} = 2^{- 4} = \frac{1}{2^{4}} = \frac{1}{16}$
x−3x5=x−3−5=x−8=1x8 $\frac{x^{- 3}}{x^{5}} = x^{- 3 - 5} = x^{- 8} = \frac{1}{x^{8}}$

Practice Problem 3

Simplify. Write each answer without negative exponents.
1. 3430 $\frac{3^{4}}{3^{0}}$
2. 55−2 $\frac{5}{5^{- 2}}$
3. 2x33x−4 $\frac{2 x^{3}}{3 x^{- 4}}$

To introduce the next rule of exponents, we consider (23)4. ${(2^{3})}^{4} .$

(23) 4 = = = 23 \cdot 23 \cdot 23 \cdot 23 a 4 = a \cdot a \cdot a \cdot a; here a = 23 . (2 \cdot 2 \cdot 2) (2 \cdot 2 \cdot 2) (2 \cdot 2 \cdot 2) (2 \cdot 2 \cdot 2) 212

$\begin{array}{rcl} {(2^{3})}^{4} & = & 2^{3} \cdot 2^{3} \cdot 2^{3} \cdot 2^{3} a^{4} = a \cdot a \cdot a \cdot a; here a = 2^{3} . \\ = & (2 \cdot 2 \cdot 2) (2 \cdot 2 \cdot 2) (2 \cdot 2 \cdot 2) (2 \cdot 2 \cdot 2) \\ = & 2^{12} \end{array}$

So (23)4=23⋅4=212. ${(2^{3})}^{4} = 2^{3 \cdot 4} = 2^{12} .$

This suggests the following rule.

Example 4 Using the Power-of-a-Power Rule of Exponents

Simplify. Write each answer without negative exponents.

(52)0 ${(5^{2})}^{0}$
[(−3)2]3 ${[{(- 3)}^{2}]}^{3}$
(x3)−1 ${(x^{3})}^{- 1}$
(x−2)−3 ${(x^{- 2})}^{- 3}$

Solution

(52)0=52⋅0=50=1 ${(5^{2})}^{0} = 5^{2 \cdot 0} = 5^{0} = 1$
[(−3)2]3=(−3)2⋅3=(−3)6=729For (−3)6, the base is −3. ${[{(- 3)}^{2}]}^{3} = {(- 3)}^{2 \cdot 3} = {(- 3)}^{6} = 729 For {(- 3)}^{6}, the base is - 3 .$
(x3)−1=x3(−1)=x−3=1x3 ${(x^{3})}^{- 1} = x^{3 (- 1)} = x^{- 3} = \frac{1}{x^{3}}$
(x−2)−3=x(−2)(−3)=x6 ${(x^{- 2})}^{- 3} = x^{(- 2) (- 3)} = x^{6}$

Practice Problem 4

Simplify. Write each answer without negative exponents.
1. (7−5)0 ${(7^{- 5})}^{0}$
2. (70)−5 ${(7^{0})}^{- 5}$
3. (x−1)8 ${(x^{- 1})}^{8}$
4. (x−2)−5 ${(x^{- 2})}^{- 5}$

We now consider the power of a product.

(2 \cdot 3) 5 = = = (2 \cdot 3) (2 \cdot 3) (2 \cdot 3) (2 \cdot 3) (2 \cdot 3) (2 \cdot 2 \cdot 2 \cdot 2 \cdot 2) (3 \cdot 3 \cdot 3 \cdot 3 \cdot 3) 25 \cdot 35 a 5 = a \cdot a \cdot a \cdot a \cdot a; here a = 2 \cdot 3. Use associative and commutative properties .

$\begin{array}{rcll} {(2 \cdot 3)}^{5} & = & (2 \cdot 3) (2 \cdot 3) (2 \cdot 3) (2 \cdot 3) (2 \cdot 3) & a^{5} = a \cdot a \cdot a \cdot a \cdot a; here a = 2 \cdot 3. \\ = & (2 \cdot 2 \cdot 2 \cdot 2 \cdot 2) (3 \cdot 3 \cdot 3 \cdot 3 \cdot 3) & Use associative and commutative properties . \\ = & 2^{5} \cdot 3^{5} \end{array}$

So (2⋅3)5=25⋅35. ${(2 \cdot 3)}^{5} = 2^{5} \cdot 3^{5} .$

This suggests the following rule.

Example 5 Using the Power-of-a-Product Rule

Simplify. Use the power-of-a-product rule to write each expression without negative exponents.

(3x)2 ${(3 x)}^{2}$
(−3x)−2 ${(- 3 x)}^{- 2}$
(−32)3 ${(- 3^{2})}^{3}$
(xy)−4 ${(x y)}^{- 4}$
(x2y)3 ${(x^{2} y)}^{3}$

Solution

(3x)2=32x2=9x2 ${(3 x)}^{2} = 3^{2} x^{2} = 9 x^{2}$
(−3x)−2=1(−3x)2=1(−3)2x2=19x2Negative exponents denote reciprocals. ${(- 3 x)}^{- 2} = \frac{1}{{(- 3 x)}^{2}} = \frac{1}{{(- 3)}^{2} x^{2}} = \frac{1}{9 x^{2}} Negative exponents denote reciprocals .$
(−32)3=(−1⋅32)3=(−1)3(32)3=(−1)(36)=−729 ${(- 3^{2})}^{3} = {(- 1 \cdot 3^{2})}^{3} = {(- 1)}^{3} {(3^{2})}^{3} = (- 1) (3^{6}) = - 729$
(xy)−4=1(xy)4=1x4y4Negative exponents denote reciprocals. ${(x y)}^{- 4} = \frac{1}{{(x y)}^{4}} = \frac{1}{x^{4} y^{4}} Negative exponents denote reciprocals .$
(x2y)3=(x2)3y3=x2⋅3y3=x6y3Recall that (x2)3=x2⋅3. ${(x^{2} y)}^{3} = {(x^{2})}^{3} y^{3} = x^{2 \cdot 3} y^{3} = x^{6} y^{3} Recall that {(x^{2})}^{3} = x^{2 \cdot 3} .$

Practice Problem 5

Simplify. Write each answer without negative exponents.
1. (12x)−1 ${(\frac{1}{2} x)}^{- 1}$
2. (5x−1)2 ${(5 x^{- 1})}^{2}$
3. (xy2)3 ${(x y^{2})}^{3}$
4. (x−2y)−3 ${(x^{- 2} y)}^{- 3}$

To see the last rule, we consider (32)5. ${(\frac{3}{2})}^{5} .$ We have

(3 2) 5 = = = 3 2 \cdot 3 2 \cdot 3 2 \cdot 3 2 \cdot 3 2 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 3 5 2 5 .

$\begin{array}{rcl} {(\frac{3}{2})}^{5} & = & \frac{3}{2} \cdot \frac{3}{2} \cdot \frac{3}{2} \cdot \frac{3}{2} \cdot \frac{3}{2} \\ = & \frac{3 \cdot 3 \cdot 3 \cdot 3 \cdot 3}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2} \\ = & \frac{3^{5}}{2^{5}} . \end{array}$

More generally, we have the following rules.

Example 6 Using the Power-of-Quotient Rules

Simplify. Use the power-of-quotient rules to write each answer without negative exponents.

(35)3 ${(\frac{3}{5})}^{3}$
(23)−2 ${(\frac{2}{3})}^{- 2}$

Solution

(35)3=3353=27125Equation (2) ${(\frac{3}{5})}^{3} = \frac{3^{3}}{5^{3}} = \frac{27}{125} Equation (2)$
(23)−2=(32)2=3222=94Equation (3) followed by equation (2) ${(\frac{2}{3})}^{- 2} = {(\frac{3}{2})}^{2} = \frac{3^{2}}{2^{2}} = \frac{9}{4} Equation (3) followed by equation (2)$

Practice Problem 6

Simplify. Write each answer without negative exponents.
1. (13)2 ${(\frac{1}{3})}^{2}$
2. (107)−2 ${(\frac{10}{7})}^{- 2}$

Warning

I n c o r r e c t (3 x) 2 (x 2) 5 x 3 x 5 = = = 3 x 2 x 7 x 15 C o r r e c t (3 x) 2 (x 2) 5 x 3 x 5 = = = 32 x 2 x 2 \cdot 5 x 3 + 5 = = = 9 x 2 x 10 x 8

$\begin{array}{c} Incorrect & Correct \\ \begin{array}{rcl} {(3 x)}^{2} & = & 3 x^{2} \\ {(x^{2})}^{5} & = & x^{7} \\ x^{3} x^{5} & = & x^{15} \end{array} & \begin{array}{rclcl} {(3 x)}^{2} & = & 3^{2} x^{2} & = & 9 x^{2} \\ {(x^{2})}^{5} & = & x^{2 \cdot 5} & = & x^{10} \\ x^{3} x^{5} & = & x^{3 + 5} & = & x^{8} \end{array} \end{array}$

Simplifying Exponential Expressions

3 Simplify exponential expressions.

Side Note

There are many correct ways to simplify exponential expressions. The order in which you apply the rules for exponents is a matter of personal preference.

Example 7 Simplifying Exponential Expressions

Simplify the following.

(−4x2y3)(7x3y) $(- 4 x^{2} y^{3}) (7 x^{3} y)$
(x52y−3)−3 ${(\frac{x^{5}}{2 y^{- 3}})}^{- 3}$

Solution

(−4x2y3)(7x3y)===(−4)(7)x2x3y3y−28x2+3y3+1−28x5y4Group factors with the same base.Apply the product rule to add exponents;remember that y=y1. $\begin{array}{rcll} (- 4 x^{2} y^{3}) (7 x^{3} y) & = & (- 4) (7) x^{2} x^{3} y^{3} y & Group factors with the same base . \\ = & - 28 x^{2 + 3} y^{3 + 1} & Apply the product rule to add exponents; \\ remember that y = y^{1} . \\ = & - 28 x^{5} y^{4} \end{array}$
(x52y−3)−3=======(x5)−3(2y−3)−3x5(−3)2−3(y−3)−3x−152−3y(−3)(−3)x−152−3y9x−15x1523x15232−3y923x15y98x15y9The exponent −3 is applied to both the numeratorand the denominator.Multiply exponents in the numerator; apply theexponent −3 to each factor in the denominator.Power rule for exponents; 5(−3)=−15.(−3)(−3)=9Multiply numerator and denominator by x1523.x−15x15=x0=1; 232−3=20=123=8 $\begin{array}{rcll} {(\frac{x^{5}}{2 y^{- 3}})}^{- 3} & = & \frac{{(x^{5})}^{- 3}}{{(2 y^{- 3})}^{- 3}} & \begin{array}{l} The exponent - 3 is applied to both the numerator \\ and the denominator . \end{array} \\ = & \frac{x^{5 (- 3)}}{2^{- 3} {(y^{- 3})}^{- 3}} & \begin{array}{l} Multiply exponents in the numerator; apply the \\ exponent - 3 to each factor in the denominator . \end{array} \\ = & \frac{x^{- 15}}{2^{- 3} y^{(- 3) (- 3)}} & Power rule for exponents; 5 (- 3) = - 15. \\ = & \frac{x^{- 15}}{2^{- 3} y^{9}} & (- 3) (- 3) = 9 \\ = & \frac{x^{- 15} x^{15} 2^{3}}{x^{15} 2^{3} 2^{- 3} y^{9}} & Multiply numerator and denominator by x^{15} 2^{3} . \\ = & \frac{2^{3}}{x^{15} y^{9}} & x^{- 15} x^{15} = x^{0} = 1; 2^{3} 2^{- 3} = 2^{0} = 1 \\ = & \frac{8}{x^{15} y^{9}} & 2^{3} = 8 \end{array}$

Practice Problem 7

Simplify each expression.
1. (2x4)−2 ${(2 x^{4})}^{- 2}$
2. x2(−y)3(xy2)3 $\frac{x^{2} {(- y)}^{3}}{{(x y^{2})}^{3}}$

Scientific Notation

4 Use scientific notation.

Scientific measurements and calculations often involve very large or very small positive numbers. For example, 1 gram of oxygen contains approximately

37, 600, 000, 000, 000, 000, 000, 000 atoms

$37, 600, 000, 000, 000, 000, 000, 000 atoms$

and the mass of one oxygen atom is approximately

0.0000000000000000000000266 gram .

$0.0000000000000000000000266 gram .$

Such numbers contain so many zeros that they are awkward to work with in calculations. Fortunately, scientific notation provides a better way to write and work with such large and small numbers.

Scientific notation consists of the product of a number less than 10, and greater than or equal to 1, and an integer power of 10. That is, scientific notation of a number has the form

c \times 10 n,

$c \times 10^{n},$

where c is a real number in decimal notation with 1≤c<10 $1 \leq c < 10$ and n is an integer.

Example 8 Converting a Decimal Number to Scientific Notation

Write each decimal number in scientific notation.

421,000
10
3.621
0.000561

Solution

Because 421,000=421000.0, $421, 000 = 421000.0,$ count five spaces to move the decimal point between the 4 and the 2 and produce the number 4.21.

Because the decimal point is moved five places to the left, the exponent is positive and we write

$421, 000 = 4.21 \times 105 .$ $421, 000 = 4.21 \times 10^{5} .$
The decimal point for 10 is to the right of the units digit. Count one place to move the decimal point between 1 and 0 and produce the number 1.0.

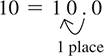
Because the decimal point is moved one place to the left, the exponent is positive and we write

$10 = 1.0 \times 101 .$ $10 = 1.0 \times 10^{1} .$
The number 3.621 is already between 1 and 10, so the decimal does not need to be moved. We write

$3.621 = 3.621 \times 100 .$ $3.621 = 3.621 \times 10^{0} .$
The decimal point in 0.000561 must be moved between the 5 and the 6 to produce the number 5.61. We count four places as follows:

Because the decimal point is moved four places to the right, the exponent is negative and we write

$0.000561 = 5.61 \times 10 - 4 .$ $0.000561 = 5.61 \times 10^{- 4} .$

Practice Problem 8

Write 732,000 in scientific notation.

Side Note

Note that in scientific notation, “small” numbers (positive numbers less than 1) have negative exponents and “large” numbers (numbers greater than 10) have positive exponents.

Example 9 Distributing Coffee and Candy in America

At the beginning of this section, we mentioned that in 2012, Americans drank about 110 billion cups of coffee and spent more than $29 billion on candy and other confectionery products. To see how these products would be evenly distributed among the population, we first convert those numbers to scientific notation.

110 billion is 110, 000, 000, 000 29 billion is 29, 000, 000, 000 = = 1.1 \times 1011 . 2.9 \times 1010 .

$\begin{array}{rcl} 110 billion is 110, 000, 000, 000 & = & 1.1 \times 10^{11} . \\ 29 billion is 29, 000, 000, 000 & = & 2.9 \times 10^{10} . \end{array}$

The U.S. population in 2012 was about 314 million, and 314 million is 314,000,000=3.14×108. $314, 000, 000 = 3.14 \times 10^{8} .$

To distribute the coffee evenly among the population, we divide:

1.1 \times 10 11 3.14 \times 10 8 = 1.10 3.14 \times 10 11 10 8 = 110 314 \times 10 11 - 8 \approx 0.35 \times 103 = 350 cups per person .

$\frac{1.1 \times 10^{11}}{3.14 \times 10^{8}} = \frac{1.10}{3.14} \times \frac{10^{11}}{10^{8}} = \frac{110}{314} \times 10^{11 - 8} \approx 0.35 \times 10^{3} = 350 cups per person .$

To distribute the cost of the candy evenly among the population, we divide:

2.9 \times 10 10 3.14 \times 10 8 = 2.90 3.14 \times 10 10 10 8 = 290 314 \times 10 10 - 8 \approx 0.92 \times 102 = 92,

$\frac{2.9 \times 10^{10}}{3.14 \times 10^{8}} = \frac{2.90}{3.14} \times \frac{10^{10}}{10^{8}} = \frac{290}{314} \times 10^{10 - 8} \approx 0.92 \times 10^{2} = 92,$

or about $92 per person.

Practice Problem 9

If the amount spent on candy consumption remains unchanged when the U.S. population reaches 325 million, what is the cost per person when cost is distributed evenly throughout the population?

Section P.2 Exercises

Concepts and Vocabulary

In the expression 7−2, $7^{- 2},$ the number −2 $- 2$ is called the .
In the expression −37, $- 3^{7},$ the base is .
The number 14−2 $\frac{1}{4^{- 2}}$ simplifies to the positive integer .
The power-of-a-product rule allows us to rewrite (5a)3 ${(5 a)}^{3}$ as .
True or False. (−11)10=−1110. ${(- 11)}^{10} = - 11^{10} .$
True or False. The exponential expression (x2)3 ${(x^{2})}^{3}$ is considered simplified.
True or False. (ab)n=anbn ${(a b)}^{n} = a^{n} b^{n}$
True or False. (a+b)n=an+bn ${(a + b)}^{n} = a^{n} + b^{n}$

Building Skills

In Exercises 9–46, evaluate each expression.

3−2 $3^{- 2}$
2−3 $2^{- 3}$
(12)−4 ${(\frac{1}{2})}^{- 4}$
(−12)−2 ${(- \frac{1}{2})}^{- 2}$
70 $7^{0}$
(−8)0 ${(- 8)}^{0}$
−(−7)0 $- {(- 7)}^{0}$
(2–√)0 ${(\sqrt{2})}^{0}$
(23)2 ${(2^{3})}^{2}$
(32)3 ${(3^{2})}^{3}$
(32)−2 ${(3^{2})}^{- 2}$
(72)−1 ${(7^{2})}^{- 1}$
(5−2)3 ${(5^{- 2})}^{3}$
(5−1)3 ${(5^{- 1})}^{3}$
(4−3)⋅(45) $(4^{- 3}) \cdot (4^{5})$
(7−2)⋅(73) $(7^{- 2}) \cdot (7^{3})$
(3–√)0+100 ${(\sqrt{3})}^{0} + 10^{0}$
(5–√)0−90 ${(\sqrt{5})}^{0} - 9^{0}$
3−2+(13)2 $3^{- 2} + {(\frac{1}{3})}^{2}$
5−2+(15)2 $5^{- 2} + {(\frac{1}{5})}^{2}$
−2−3 $- 2^{- 3}$
−3−2 $- 3^{- 2}$
(−3)−2 ${(- 3)}^{- 2}$
(−2)−3 ${(- 2)}^{- 3}$
211210 $\frac{2^{11}}{2^{10}}$
3638 $\frac{3^{6}}{3^{8}}$
(53)4512 $\frac{{(5^{3})}^{4}}{5^{12}}$
(95)298 $\frac{{(9^{5})}^{2}}{9^{8}}$
25⋅3−224⋅3−3 $\frac{2^{5} \cdot 3^{- 2}}{2^{4} \cdot 3^{- 3}}$
4−2⋅534−3⋅5 $\frac{4^{- 2} \cdot 5^{3}}{4^{- 3} \cdot 5}$
−5−22−1 $\frac{- 5^{- 2}}{2^{- 1}}$
−7−23−1 $\frac{- 7^{- 2}}{3^{- 1}}$
(23)−1 ${(\frac{2}{3})}^{- 1}$
(15)−1 ${(\frac{1}{5})}^{- 1}$
(23)−2 ${(\frac{2}{3})}^{- 2}$
(32)−2 ${(\frac{3}{2})}^{- 2}$
(117)−2 ${(\frac{11}{7})}^{- 2}$
${(\frac{13}{5})}^{- 2}$

In Exercises 47–86, simplify each expression. Write your answers without negative exponents. Whenever an exponent is negative or zero, assume that the base is not zero.

$x^{4} y^{0}$
$x^{- 1} y^{0}$
$x^{- 1} y$
$x^{2} y^{- 2}$
$x^{- 1} y^{- 2}$
$x^{- 3} y^{- 2}$
${(x^{- 3})}^{4}$
${(x^{- 5})}^{2}$
${(x^{- 11})}^{- 3}$
${(x^{- 4})}^{- 12}$
$- 3 {(x y)}^{5}$
$- 8 {(x y)}^{6}$
$4 {(x y^{- 1})}^{2}$
$6 {(x^{- 1} y)}^{3}$
$3 {(x^{- 1} y)}^{- 5}$
$- 5 {(x y^{- 1})}^{- 6}$
$\frac{{(x^{3})}^{2}}{{(x^{2})}^{5}}$
$\frac{x^{2}}{{(x^{3})}^{4}}$
${(\frac{2 x y}{x^{2}})}^{3}$
${(\frac{5 x y}{x^{3}})}^{4}$
${(\frac{- 3 x^{2} y}{x})}^{5}$
${(\frac{- 2 x y^{2}}{y})}^{3}$
${(\frac{- 3 x}{5})}^{- 2}$
${(\frac{- 5 y}{3})}^{- 4}$
${(\frac{4 x^{- 2}}{x y^{5}})}^{3}$
${(\frac{3 x^{2} y}{y^{3}})}^{5}$
$\frac{x^{3} y^{- 3}}{x^{- 2} y}$
$\frac{x^{2} y^{- 2}}{x^{- 1} y^{2}}$
$\frac{27 x^{- 3} y^{5}}{9 x^{- 4} y^{7}}$
$\frac{15 x^{5} y^{- 2}}{3 x^{7} y^{- 3}}$
$\frac{1}{x^{3}} {(x^{2})}^{3} x^{- 4}$
${(8 a^{3} b)}^{- 4} {(\frac{2 a}{b})}^{12}$
${(- x y^{2})}^{3} {(- 2 x^{2} y^{2})}^{- 4}$
${[\frac{{(- x^{2} y)}^{3} y^{- 4}}{{(x y)}^{5}}]}^{- 2}$
${(4 x^{3} y^{2} z)}^{2} {(x^{3} y^{2} z)}^{- 7}$
$\frac{{(2 x y z)}^{2}}{{(x^{3} y)}^{2} {(x z)}^{- 1}}$
$\frac{5 a^{- 2} b c^{2}}{a^{4} b^{- 3} c^{2}}$
$\frac{{(- 3)}^{2} a^{5} {(b c)}^{2}}{{(- 2)}^{3} a^{2} b^{3} c^{4}}$
${(\frac{x y^{- 3} z^{- 2}}{x^{2} y^{- 4} z^{3}})}^{- 3}$
${(\frac{x y^{- 2} z^{- 1}}{x^{- 5} y z^{- 8}})}^{- 1}$

In Exercises 87–94, write each number in scientific notation.

125
247
850,000
205,000
0.007
0.0019
0.00000275
0.0000038

Applying the Concepts

In Exercises 95 and 96, use the fact that when you uniformly stretch or shrink a three-dimensional object in every direction by a factor of a, the volume of the resulting figure is scaled by a factor of $a^{3} .$ For example, when you uniformly scale (stretch or shrink) a three-dimensional object by a factor of 2, the volume of the resulting figure is scaled by a factor of $2^{3},$ or 8.

A display in the shape of a baseball bat has a volume of 135 cubic feet. Find the volume of the display that results by uniformly scaling the figure by a factor of 2.
A display in the shape of a football has a volume of 675 cubic inches. Find the volume of the display that results by uniformly scaling the figure by a factor of $\frac{1}{3}$ .
The area A of a square with side of length x is given by $A = x^{2} .$ Use this relationship to
1. verify that doubling the length of the side of a square floor increases the area of the floor by a factor of $2^{2} .$
2. verify that tripling the length of the side of a square floor increases the area of the floor by a factor of $3^{2} .$
The area A of a circle with diameter d is given by $A = π {(\frac{d}{2})}^{2} .$ Use this relationship to
1. verify that doubling the length of the diameter of a circular skating rink increases the area of the rink by a factor of $2^{2} .$
2. verify that tripling the length of the diameter of a circular skating rink increases the area of the rink by a factor of $3^{2} .$
The cross section of one type of weight-bearing rod (the surface you would get if you sliced the rod perpendicular to its axis) used in the Olympics is a square, as shown in the accompanying figure. The rod can handle a stress of 25,000 pounds per square inch (psi). The relationship between the stress S the rod can handle, the load F the rod can carry, and the width w of the cross section is given by the equation $S w^{2} = F .$ Assuming that $w = 0.25$ inch, find the load the rod can support.
The cross section of one type of weight-bearing rod (the surface you would get if you sliced the rod perpendicular to its axis) used in the Olympics is a circle, as shown in the figure. The rod can handle a stress of 10,000 pounds per square inch (psi). The relationship between the stress S the rod can handle, the load F the rod can carry, and the diameter d of the cross section is given by the equation $S π {(d / 2)}^{2} = F .$ Assuming that $d = 1.5$ inches, find the load the rod can support. Use $π \approx 3.14$ in your calculation.
A year has 365.25 days. Write the number of seconds in one year in scientific notation.
Repeat Exercise 101 for a leap year (366 days).

Complete the following table.

Celestial Body	Equatorial Diameter (km)	Scientific Notation
Earth	12,700
Moon		$3.48 \times 10^{3} (km)$
Sun	1,390,000
Jupiter		$1.34 \times 10^{5} (km)$
Mercury	4800

In Exercises 104–110, express the number in each statement in scientific notation.

One gram of oxygen contains about

$37, 600, 000, 000, 000, 000, 000, 000 atoms .$
One gram of hydrogen contains about

$602, 000, 000, 000, 000, 000, 000 atoms .$
One oxygen atom weighs about

$0.0000000000000000000266 kilogram .$
One hydrogen atom weighs about

$0.00000000000000000000167 kilogram .$
The distance from Earth to the moon is about

$380, 000, 000 meters .$
The mass of Earth is about

$5, 980, 000, 000, 000, 000, 000, 000, 000 kilograms .$
The mass of the sun is about

$2, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000 kilograms .$

Beyond the Basics

If $2^{x} = 32,$ find
1. $2^{x + 2}$
2. $2^{x - 1}$
If $3^{x} = 81,$ find
1. $3^{x + 1}$
2. $3^{x - 2}$
If $5^{x} = 11,$ find
1. $5^{x + 1}$
2. $5^{x - 2}$
If $a^{x} = b,$ find
1. $a^{x + 2}$
2. $a^{x - 1}$
Simplify: $\frac{3^{2 - n} \cdot 9^{2 n - 2}}{3^{3 n}}$
Simplify: $\frac{2^{m + 1} \cdot 3^{2 m - n} \cdot 5^{m + n + 2} \cdot 6^{n}}{6^{m} \cdot 10^{n + 1} \cdot 15^{m}}$

[Hint: $6 = 2 \cdot 3, 10 = 2 \cdot 5, 15 = 3 \cdot 5$ ]
Simplify: $\frac{2^{x (y - z)}}{2^{y (x - z)}} \div {(\frac{2^{y}}{2^{x}})}^{z}$
Simplify: ${(\frac{a^{x}}{a^{y}})}^{\frac{1}{x y}} \cdot {(\frac{a^{y}}{a^{z}})}^{\frac{1}{y z}} \cdot {(\frac{a^{z}}{a^{x}})}^{\frac{1}{x z}}$

Getting Ready for the Next Section

Simplify:
1. $x^{2} \cdot x^{5}$
2. $(2 x) (- 5 x^{2})$
3. $(2 y^{2}) (3 y^{3}) (4 y^{5})$
Simplify:
1. $2 x^{2} + 5 x^{2}$
2. $3 x^{2} - 4 x^{2}$
3. $3 x^{3} - 5 x^{3} + 11 x^{3}$
True or False: $5 x^{2} + 3 x^{3} = 8 x^{5}$
Use the distributive property to simplify: $2 x^{2} (5 x^{3} - 3 x + 4)$

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Product Rule: am⋅an=am+n $a^{m} \cdot a^{n} = a^{m + n}$	Quotient Rule: aman=am−n $\frac{a^{m}}{a^{n}} = a^{m - n}$
Power-of-Power Rule: (am)n=amn ${(a^{m})}^{n} = a^{m n}$	Power-of-a-Product Rule: (ab)m=ambm ${(a b)}^{m} = a^{m} b^{m}$
Power-of-Quotient Rules: (ab)n=anbn; (ab)−n=(ba)n=bnan,b≠0 ${(\frac{a}{b})}^{n} = \frac{a^{n}}{b^{n}}; {(\frac{a}{b})}^{- n} = {(\frac{b}{a})}^{n} = \frac{b^{n}}{a^{n}}, b \neq 0$

Table of Contents for Section P.2 Integer Exponents and Scientific Notation

Create new playlist

Sign In

Sign Up

Table of Contents for
Section P.2 Integer Exponents and Scientific Notation