- MyLab Math Online Course for College Algebra by Ratti, McWaters, Skrzypek (access code required)
- Connect the Concepts and Relate the Math
- College Algebra
- College Algebra
- Foreword
- Contents
- Preface
- Get the Most Out of MyLab Math
- Resources for Success
- Dedication
- Chapter P Basic Concepts of Algebra
- Topics
- Section P.1 The Real Numbers and Their Properties
- Before Starting This Section, Review From Your Previous Mathematics Texts
- Objectives
- Classifying Numbers
- Equality of Numbers
- Classifying Sets of Numbers
- Rational Numbers
- Irrational Numbers
- Integer Exponents
- The Real Number Line
- Inequalities
- Sets
- Definition of Union and Intersection
- Intervals
- Absolute Value
- Distance Between Two Points on a Real Number Line
- Order of Operations
- Properties of the Real Numbers
- Subtraction and Division of Real Numbers
- Algebraic Expressions
- Section P.1 Exercises
- Section P.2 Integer Exponents and Scientific Notation
- Section P.3 Polynomials
- Section P.4 Factoring Polynomials
- Before Starting This Section, Review
- Objectives
- The Greatest Common Monomial Factor
- Factoring Out a Monomial
- Factoring Trinomials of the Form x2+Bx+C
- Factoring Formulas
- Perfect-Square Trinomials
- Difference of Squares
- Difference and Sum of Cubes
- Factoring by Grouping
- Factoring Trinomials of the Form Ax2+Bx+C
- Section P.4 Exercises
- Section P.5 Rational Expressions
- Section P.6 Rational Exponents and Radicals
- Chapter P Review and Tests
- Review Exercises
- Practice Test
- Chapter 1 Equations and Inequalities
- Topics
- Section 1.1 Linear Equations in One Variable
- Section 1.2 Applications of Linear Equations: Modeling
- Section 1.3 Quadratic Equations
- Section 1.4 Complex Numbers: Quadratic Equations with Complex Solutions
- Section 1.5 Solving Other Types of Equations
- Section 1.6 Inequalities
- Section 1.7 Equations and Inequalities Involving Absolute Value
- Chapter 1 Review and Tests
- Review Exercises
- Practice Test A
- Practice Test B
- Chapter 2 Graphs and Functions
- Topics
- Section 2.1 The Coordinate Plane
- Section 2.2 Graphs of Equations
- Section 2.3 Lines
- Section 2.4 Functions
- Section 2.5 Properties of Functions
- Section 2.6 A Library of Functions
- Section 2.7 Transformations of Functions
- Section 2.8 Combining Functions; Composite Functions
- Before Starting this Section, Review
- Objectives
- Combining Functions
- Composition of Functions
- Domain of Composite Functions
- Decomposition of a Function
- Applications of Composite Functions
- Section 2.8 Exercises
- Section 2.9 Inverse Functions
- Before Starting this Section, Review
- Objectives
- Inverses
- Finding the Inverse Function
- Solution
- Practice Problem 5
- Practice Problem 6
- Finding the Range of a One-to-One Function
- Applications
- Chapter 3 Polynomial and Rational Functions
- Section 3.3 Dividing Polynomials
- Section 3.4 The Real Zeros of a Polynomial Function
- Section 3.5 The Complex Zeros of a Polynomial Function
- Section 3.6 Rational Functions
- Section 3.7 Variation
- Chapter 3 Review and Tests
- Review Exercises
- Practice Test A
- Practice Test B
- Cumulative Review Exercises Chapters P–3
- Chapter 4 Exponential and Logarithmic Functions
- Topics
- Section 4.1 Exponential Functions
- Before Starting this Section, Review
- Objectives
- Exponential Functions
- Evaluate Exponential Functions
- Graphing Exponential Functions
- Transformations on Exponential Functions
- Simple Interest
- Compound Interest
- Continuous Compound Interest Formula
- The Natural Exponential Function
- Exponential Growth and Decay
- Section 4.1 Exercises
- Section 4.2 Logarithmic Functions
- Section 4.3 Rules of Logarithms
- Section 4.4 Exponential and Logarithmic Equations and Inequalities
- Section 4.5 Logarithmic Scales; Modeling
- Chapter 4 Review and Tests
- Review Exercises
- Practice Test A
- Practice Test B
- Cumulative Review Exercises Chapters P–4
- Chapter 5 Systems of Equations and Inequalities
- Topics
- Section 5.1 Systems of Linear Equations in Two Variables
- Section 5.2 Systems of Linear Equations in Three Variables
- Section 5.3 Partial-Fraction Decomposition
- Section 5.4 Systems of Nonlinear Equations
- Section 5.5 Systems of Inequalities
- Section 5.6 Linear Programming
- Chapter 5 Review and Tests
- Chapter 6 Matrices and Determinants
- Topics
- Section 6.1 Matrices and Systems of Equations
- Section 6.2 Matrix Algebra
- Section 6.3 The Matrix Inverse
- Section 6.4 Determinants and Cramer’s Rule Determinants and Cramer’s Rule
- Chapter 6 Review and Tests
- Review Exercises
- Practice Test A
- Practice Test B
- Cumulative Review Exercises Chapters P–6
- Chapter 7 Conic Sections
- Topics
- Section 7.1 Conic Sections: Overview
- Section 7.2 The Parabola
- Section 7.3 The Ellipse
- Section 7.4 The Hyperbola
- Chapter 7 Review and Tests
- Review Exercises
- Practice Test A
- Practice Test B
- Cumulative Review Exercises Chapters P–7
- Chapter 8 Further Topics in Algebra
- Topics
- Section 8.1 Sequences and Series
- Section 8.2 Arithmetic Sequences; Partial Sums
- Section 8.3 Geometric Sequences and Series
- Section 8.4 Mathematical Induction
- Section 8.5 The Binomial Theorem
- Section 8.6 Counting Principles
- Section 8.7 Probability
- Chapter 8 Review and Tests
- Review Exercises
- Practice Test A
- Practice Test B
- Cumulative Review Exercises Chapters P–8
- Answers
- Chapter P
- Chapter 1
- Chapter 2
- Chapter 3
- Chapter 4
- Chapter 5
- Chapter 6
- Chapter 7
- Chapter 8
- Credits
- Index
- Algebra–Formulas and Definitions
- Geometry–Formulas
Beyond the Basics
97. Stretch the graph of
y=1x vertically by a factor of 2 and reflect the graph about the x-axis.
99. Shift the graph of
y=1x2 two units to the right.
101. Shift the graph of
y=1x2 one unit to the right and two units down.
103. Shift the graph of
y=1x2 six units to the left.
105. Shift the graph of
y=1x2 one unit to the right and one unit up.
-
f (x)→0 asx →−∞, f (x)→0 asx →∞, f (x)→−∞ asx→0−, andf (x)→∞ asx →0+; no x-intercept; no y-intercept; vertical asymptote: y-axis; horizontal asymptote: x-axis. The graph is above the x-axis on(0, ∞) and below the x-axis on(−∞, 0). 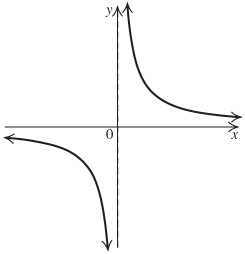
f (x)→0 asx →−∞, f(x)→0 asx→∞, f (x)→∞ asx→0−, andf (x)→−∞ asx→0+; no x-intercept; no y-intercept; vertical asymptote: y-axis; horizontal asymptote: x-axis. The graph is above the x-axis on(−∞, 0) and below the x-axis on(0, ∞). 
f (x)→0 asx →∞, f (x)→0 asx→−∞, f (x)→∞ asx→0−, andf (x)→∞ asx→0+; no x-intercept; no y-intercept; vertical asymptote: y-axis; horizontal asymptote: x-axis. The graph is above the x-axis on(−∞, 0)∪(0, ∞). 
f (x)→0 asx →−∞, f (x)→0 asx→∞, f (x)→−∞ asx→0−, andf (x)→−∞ asx→0+; no x-intercept; no y-intercept; vertical asymptote: y-axis; horizontal asymptote: x-axis. The graph is below the x-axis on(−∞, 0)∪(0, ∞). 
-

111.
[f (x)]−1=12x+3 andf−1(x)=12x−32. The two functions are different.
113. g(x) has the oblique asymptote
y=2x+3; y→−∞ asx →−∞, andy →∞ asx →∞. 
115. Point of intersection:
(−13, 1); horizontal asymptotey=1 
117.
f(x)=2−xx−3 119.
f(x)=−x2+1x 121.
f(x)=(x+4)/(x−2) 123.
f(x)=(4x2−1)/(x−1)2 125.
f(x)=(3x2−x+1)/(x−1)
-
No Comment
