Section 3.4 The Real Zeros of a Polynomial Function
Before Starting this Section, Review
1 Synthetic division (Section 3.3 , page 355)
2 Zero-product property (Section 1.3 , page 106)
3 Multiplicity of a zero (Section 3.2 , page 340)
Objectives
 Dow Jones Industrial Average
Dow Jones Industrial Average
The Dow Jones Industrial Average (DJIA) reflects the average cost per share of stock from 30 companies chosen by the board of the New York Stock Exchange as the most outstanding companies to provide a quantitative view of the stock market and, by extension, the U.S. economy. To calculate the DJIA on any day, we do not simply add the prices of the component stocks and divide by 30. The reason is that during the past 100-plus years, there have been many stock splits, spinoffs, and stock substitutions. Without making an adjustment to the divisor (30), the value of the DJIA would be distorted.
To understand this, consider a stock split. Suppose two stocks are trading at $10 and $40; the average of the two is $25. If the company with $40 stock has a two-for-one split, its shares are now priced at $20 each. The average of the two stocks falls to $15(10+202=15).
Over time, the divisor 30 for the DJIA has been adjusted several times, mostly downward. It stood at 0.001960784 in September 2013. This explains why the DJIA can be reported as 15,300 even though the sum of the prices of all of its component stocks is a fraction of this number. In Exercise 85, we model an investment between 2004 and 2013 by a polynomial function.

Real Zeros of a Polynomial Function
1 Review real zeros of polynomials.
We first review what we have learned about the real zeros of a polynomial function.
Definition If c is a real number in the domain of a function f and f(c)=0, then c is called a real zero of f.
Geometrically, this means that the graph of f has an x-intercept at c.
Algebraically, this means that (x−c) is a factor of f(x). In other words, we can write f(x)=(x−c)g(x) for some polynomial function g(x).
Number of real zeros A polynomial function of degree n has, at most, n real zeros.
Polynomial in factored form If a polynomial F(x) can be written in factored form, we find its zeros by solving F(x)=0 using the zero-product property of real numbers.
Intermediate Value Theorem If a polynomial F(x) cannot be factored, we find approximate values of the real zeros (if any) of F(x) by using the Intermediate Value Theorem. See page 339.
In this section, we investigate other useful tools for finding the real zeros of a polynomial function.
Rational Zeros Theorem
2 Use the Rational Zeros Theorem.
We use the following test (see Exercise 103 for a proof) to find possible rational zeros of a polynomial function with integer coefficients. We then use the Factor Theorem to determine whether any of these numbers is, in fact, a zero of a polynomial function F(x).
Example 1 Using the Rational Zeros Theorem
Find all rational zeros of F(x)=2x3+5x2−4x−3.
Solution
First, we list all possible rational zeros of F(x).
All combinations for the rational zeros can be found by using just the positive factors of the leading coefficient. The possible rational zeros are

or
We use synthetic division to determine whether a rational zero exists among these eight candidates. We start by testing 1. If 1 is not a rational zero, we will test other possibilities.

The zero remainder tells us that (x−1) is a factor of F(x), with the other factor being 2x2+7x+3. So
We find the zeros of F(x) by solving the equation (x−1)(2x+1)(x+3)=0.
The solution set is {1, −12, −3}. The rational zeros of F are −3,−12, and 1.
In Example 1 we were able to completely factor the polynomial function F(x)=2x3+5x2−4x−3=(x−1)(2x+1)(x+3). Applying the techniques from Section 3.2 allows us to sketch the graph of y=f(x) (see Figure 3.19).

Figure 3.19
Practice Problem 1
Find all rational zeros of F(x)=2x3+3x2−6x−8.
Recall that the zeros of a polynomial function y=F(x) are also the roots or the solutions of the polynomial equation F(x)=0.
 Warning
Warning
The rational zeros Theorem only identifies the possible rational zeros. It does not identify which, if any, are actual zeros.
Example 2 Solving a Polynomial Equation
Solve 3x3−8x2−8x+8=0.
Solution

The graph of y=3x3−8x2−8x+8 is shown in Figure 3.20. The calculator graph is shown in the margin.

Figure 3.20
Graph of y=3x3−8x2−8x+8
From the graph in Figure 3.20, it appears that an x-intercept is between 0.5 and 1. We check whether x=23 is a root by synthetic division.

Because the remainder in the synthetic division is 0,(x−23) is a factor of the original equation with the depressed equation 3x2−6x−12=0.
You can see from the graph in Figure 3.20 that 1±√5 are also the x-intercepts of the graph.
The three real roots of the given equation are
Practice Problem 2
Solve 2x3−9x2+6x−1=0.
Side Note
Because 3x2−6x−12=3(x2−2x−4) you could use the quadratic formula to just solve x2−2x−4 in this example. of course, you again find x=1±√5
Example 2 illustrates the following Theorem.
Descartes’s Rule of Signs
3 Find the possible number of positive and negative zeros of polynomials.
Descartes’s Rule of Signs is used to find the possible number of positive and negative zeros of a polynomial function.
If the terms of a polynomial are written in descending order, we say that a variation of sign occurs when the signs of two consecutive terms differ. For example, in the polynomial 2x5−5x3−6x2+7x+3, the signs of the terms are +−−++. Therefore, there are two variations of sign, as follows:

There are three variations of sign in
Example 3 Using Descartes’s Rule of Signs
Find the possible number of positive and negative zeros of
Solution
There are three variations of sign in f(x).

The number of positive zeros of f(x) must be 3 or 3−2=1. Furthermore,

The polynomial f(−x) has two variations of sign; therefore, the number of negative zeros of f(x) is 2 or 2−2=0.
Practice Problem 3
Find the possible number of positive and negative zeros of
f(x)=2x5+3x2+5x−1.
Bounds on the Real Zeros
4 Find the bounds on the real zeros of polynomials.
If a polynomial function F(x) has no zeros greater than a number k, then k is called an upper bound on the zeros of F(x). Similarly, if F(x) has no zeros less than a number k, then k is called a lower bound on the zeros of F(x). These bounds are found by using the following rules.
Side Note
When deciding whether numbers “alternate in sign” we consider 0 as positive or negative as required to count as alternating.
Example 4 Finding the Bounds on the Zeros
Find upper and lower bounds on the zeros of
Solution
By the Rational Zeros Theorem, the possible rational zeros of F(x) are ±1, ±2, ±3, and ±6. There is only one variation of sign in F(x)=x4−x3−5x2−x−6, so F(x) has only one positive zero. First, we try synthetic division by x−k with k=1, 2, 3, . … The first integer that makes each number in the last row a 0 or a positive number is an upper bound on the zeros of F(x).
By the rule for bounds, 3 is an upper bound on the zeros of F(x).
We now try synthetic division by x−k with k=−1, −2, −3, …. The first negative integer for which the numbers in the last row alternate in sign is a lower bound on the zeros of F(x).
By the rule of bounds, −2 is a lower bound on the zeros of F(x).
Practice Problem 4
Find upper and lower bounds on the zeros of
f(x)=2x3+5x2+x−2.
Side Note
When checking the positive integers (k=1,2,3,…) for an upper bound on the zeros of a function, also check the last row for alternating signs indicating a lower bound. For example, for f(x)=x3−9x2+26x−24, when checking k=1, we have

so 1 is a lower bound.
An upper bound or a lower bound on the zeros of a polynomial function is not unique. For example, the zeros of P(x)=x3+2x2−x−2 are −2,−1, and 1. Any number greater than or equal to 1 is an upper bound on these zeros, and any number less than or equal to −2 is a lower bound on these zeros.
Find the Real Zeros of a Polynomial Function
5 Learn a procedure for finding the real zeros of a polynomial function.
We outline steps for gathering information and locating the real zeros of a polynomial function.
Step 1 Find the maximum number of real zeros by using the degree of the polynomial function.
Step 2 Find the possible number of positive and negative zeros by using Descartes’s Rule of Signs.
Step 3 Write the set of possible rational zeros.
Step 4 Test the smallest positive integer in the set in Step 3, the next larger, and so on, until an integer zero or an upper bound of the zeros is found.
If a zero is found, use the function represented by the depressed equation in further calculations.
If an upper bound is found, discard all larger numbers in the set of possible rational zeros.
Step 5 Test the positive fractions that remain in the set in Step 3 after considering any bound that has been found.
Step 6 Use modified Steps 4 and 5 for negative numbers in the set in Step 3.
Step 7 If a depressed equation is quadratic, use any method (including the quadratic formula) to solve this equation.
Side Note
A graphing calculator may be used to obtain the approximate location of the real zeros. For a rational zero, verify by using synthetic division.
Example 5 Finding the Real Zeros of a Polynomial Function
Find the real zeros of f(x)=2x5−x4−14x3+7x2+24x−12.
Solution
Step 1 The degree of f is 5; so f has, at most, 5 real zeros.
Step 2

There are three variations of sign in f(x). So f has 3 or 1 positive zeros.

There are two variations of signs in f(−x). So f has 2 or 0 negative zeros.
Step 3 Possible rational zeros are
{±1, ±2, ±3, ±4, ±6, ±12, ±12, ±32}.Step 4 We test for zeros, 1, 2, 3, 4, 6, and 12 until a zero or an upper bound is found.

Because 2 is a zero, (x−2) is a factor of f. We have
f(x)=(x−2)(2x4+3x3−8x2−9x+6)Synthetic divisionWe consider the zeros of Q1(x)=2x4+3x3−8x2−9x+6.
The possible positive rational zeros of Q1(x) are {1,2,3,6,12,32}. We discard 1 because 1 is not a zero of the original function. We test 2 because it may be a repeated zero of f.

The last row shows that 2 is not a zero of Q1(x) but is an upper bound (all entries in the last row are positive) for the zeros of Q1(x), hence, also on the zeros of f.
Step 5 We test the remaining positive entries 12 and 32 in the list.

Note that 12 is a zero of Q1(x). Using the last row in synthetic division, we have
f(x)=(x−2)(x−12)(2x3+4x2−6x−12)=0or (x−2)(2x−1)(x3+2x2−3x−6)=0Simplify.Step 6 We now find the negative zeros of Q2(x)=x3+2x2−3x−6. We test −1,−2,−3, and −6.

Step 7 We can solve the depressed equation x2−3=0 to obtain x=±√3. The real zeros of f are −2,−√3,12,√3, and 2. Because f(x) has, at most, five real zeros, we have found all of them.
Practice Problem 5
Find the real zeros of f(x)=3x4−11x3+22x−12.
Example 6 Graphing a Polynomial Function
Sketch the graph of f(x)=3x3−2x2−6x+4.
Solution
We use the procedure given in Section 3.2 on page 342.
Step 1 Because the degree, 3, is odd and the leading coefficient, 3, is positive, the end behavior is similar to that of y=x3.
Step 2 Solve 3x3−2x2−6x+4=0 to find the real zeros. By the Rational Zeros Theorem, the possible rational roots are ±13, ±23, ±1. Trying each value, we find that 23 is a real zero, as shown below. We solve the depressed equation 3x2−6=0 to find the remaining zeros, x=±√2. The y-intercept is f(0)=3(0)3−2(0)2−6(0)+4=4.

Step 3 The y-intercept is f(0)=4. The graph passes through the point (0, 4).
Step 4 f(−x)=3(−x)3−2(−x)2−6(−x)+4=−3x3−2x2+6x+4
So f(−x) ≠f(x), and f(−x) ≠−f(x). There are no symmetries.
Step 5 The three zeros, −√2, 23, √2, divide the x-axis into four intervals:
(−∞, −√2), (−√2, 23), (23, √2), and, (√2, ∞)
Noting that √2≈1.4, we choose −2, 0, 1, and 2 as test numbers.

Step 6 The graph is shown in Figure 3.21 .

Figure 3.21
Practice Problem 6
Sketch the graph of f(x)=3x3−x2−9x+3.
Section 3.4 Exercises
Concepts and Vocabulary
Let P(x)=anxn+⋯+a0 with integer coefficients. If pq is a rational zero of P(x), then pq=possible factors of _possible factors of _.
If the terms of a polynomial are written in descending order, then a variation of sign occurs when the signs of two terms differ.
The number of positive zeros of a polynomial function P(x) is equal to the number of of sign of P(x) or is less than that number by (a)n .
If a polynomial P(x) has no zero greater than a number k, then k is called a(n) on the zeros of P(x). If P(x) has no zero less than a number m, then m is called a(n) on the zeros of P(x).
True or False. Possible rational zeros of P(x)=9x3−9x2−x+1 are ±1, ±3, ±9.
True or False. The polynomial function P(x)=x3+x+1 has exactly one real zero.
True or False. If P(x) is a polynomial with integer coefficients and −√5 is a zero for P(x), then √5 is also a zero.
True or False. The number of negative zeros of f(x)=3x4−5x3−x2+2x−4 is either 2 or 0.
Building Skills
In Exercises 9–12, find the set of possible rational zeros of the given function.
f(x)=3x3−4x2+5
g(x)=2x4−5x2−2x+1
h(x)=4x4−9x2+x+6
F(x)=6x6+5x5+x−35
In Exercises 13–28, find all rational zeros of the given polynomial function.
f(x)=x3−x2−4x+4
f(x)=x3−4x2+x+6
f(x)=x3+x2+2x+2
f(x)=x3+3x2+2x+6
g(x)=2x3+x2−13x+6
g(x)=6x3+13x2+x−2
g(x)=3x3−2x2+3x−2
g(x)=2x3+3x2+4x+6
h(x)=3x3+7x2+8x+2
h(x)=2x3+x2+8x+4
h(x)=x4−x3−x2−x−2
h(x)=2x4+3x3+8x2+3x−4
F(x)=x4−x3−13x2+x+12
G(x)=3x4+5x3+x2+5x−2
F(x)=x4−2x3+10x2−x+1
G(x)=x6+2x4+x2+2
In Exercises 29–34, graph each polynomial function.
f(x)=6x3+13x2+x−2
f(x)=2x3−x2−4x+2
f(x)=2x3−3x2−14x+21
f(x)=6x3+17x2+x−10
f(x)=4x4+4x3−3x2−2x+1
f(x)=9x4+30x3+13x2−20x+4
In Exercises 35–48, determine the possible number of positive and negative zeros of the given function by using Descartes’s Rule of Signs.
f(x)=5x3−2x2−3x+4
g(x)=3x3+x2−9x−3
f(x)=2x3+5x2−x+2
g(x)=3x4+8x3−5x2+2x−3
h(x)=2x5−5x3+3x2+2x−1
F(x)=5x6−7x4+2x3−1
G(x)=−3x4−4x3+5x2−3x+7
H(x)=−5x5+3x3−2x2−7x+4
f(x)=x4+2x2+4
f(x)=3x4+5x2+6
g(x)=2x5+x3+3x
g(x)=2x5+4x3+5x
h(x)=−x5−2x3+4
h(x)=2x5+3x3+1
In Exercises 49–56, determine integer upper and lower bounds on the zeros of the given function.
f(x)=3x3−x2+9x−3
g(x)=2x3−3x2−14x+21
F(x)=3x3+2x2+5x+7
G(x)=x3+3x2+x−4
h(x)=x4+3x3−15x2−9x+31
H(x)=3x4−20x3+28x2+19x−13
f(x)=6x4+x3−43x2−7x+7
g(x)=6x4+23x3+25x2−9x−5
In Exercises 57–76, find all rational zeros of f. Then (if necessary) use the depressed equation to find all roots of the equation f(x)=0.
f(x)=x3+5x2−8x+2
f(x)=x3−7x2−5x+3
f(x)=2x3−x2−6x+3
f(x)=3x3+2x2−15x−10
f(x)=2x3−9x2+6x−1
f(x)=2x3−3x2−4x−1
f(x)=x4+x3−5x2−3x+6
f(x)=x4−2x3−5x2+4x+6
f(x)=x4−3x3+3x−1
f(x)=x4−6x3−7x2+54x−18
f(x)=2x4−5x3−4x2+15x−6
f(x)=3x4−8x3−18x2+40x+15
f(x)=6x4−x3−13x2+2x+2
f(x)=6x4+x3−19x2−3x+3
f(x)=x5−2x4−4x3+8x2+3x−6
f(x)=x5+x4−6x3−6x2+8x+8
f(x)=2x5+x4−11x3−x2+15x−6
f(x)=2x5−x4−9x3+10x+4
f(x)=2x5−13x4+27x3−17x2−5x+6
f(x)=3x5+x4−9x3−3x2+6x+2
Applying the Concepts
Geometry. The length of a rectangle is x2−2x+3, and its width is x−2. Find its dimensions, assuming that its area is 306 square units.
Making a box. A square piece of tin 18 inches on each side is to be made into a box without a top by cutting a square from each corner and folding up the flaps to form the sides. What size corners should be cut so that the volume of the box is 432 cubic inches?

Cost function. The total cost of a product (in dollars) is given by C(x)=3x3−6x2+108x+100, where x is the demand for the product. Find the value of x that gives a total cost of $628.
Profit. For the product in Exercise 79, the demand function is p(x)=330+10x−x2. Find the value of x that gives the profit of $910.
Production cost. The total cost per month, in thousands of dollars, of producing x printers (with x measured in hundreds) is given by C(x)=x3−15x2+5x+50. How many units must be produced so that the total monthly cost is $125,000?
Break even. If the demand function for the printers in Exercise 81 is p(x)=−3x+3+74x, find the number of printers that must be produced and sold to break even.
Oil import-export. A country maintains its normal oil needs by importing the deficit and exporting its surplus oil. The accompanying graph shows the country’s balance of import (−) and export (+) (in million barrels) for 2007–2016, where x=0 represents 2007.
How many years did the country export oil?
Construct a polynomial function of minimum degree that models this graph.
Use part (b) to estimate the oil import or export in 2012.

Number of tourists. The accompanying graph shows the number of tourists (in thousands) above (+) or below (−) normal during 2016, where x=1 represents January.
Construct a polynomial function of minimum degree that models this graph.
Use part (a) to estimate the level of tourism in September. 2016.
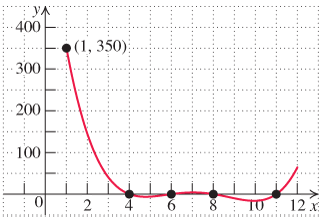
 Investment. The accompanying graph shows the profit/loss (in thousand dollars) of Ms. Sharpy’s investment in the stock market during 2004–2013, where x=0 represents 2004.
Investment. The accompanying graph shows the profit/loss (in thousand dollars) of Ms. Sharpy’s investment in the stock market during 2004–2013, where x=0 represents 2004.Construct a polynomial of minimum degree that models the graph.
Use part (a) to estimate the profit/loss in 2008.

Use part (a) to determine the year(s) when Ms. Sharpy realized a profit of $600.
 Use part (a) to determine the maximum profit and the year it occurred.
Use part (a) to determine the maximum profit and the year it occurred.
Shipping containers. When two shipping containers in the shape of a cube were put side-by-side, it turned out that one was 2 feet taller than the other. If the combined volume of the two containers is 152 ft3, what are their respective dimensions?
Beyond the Basics
In Exercises 87–90, show that the given number is irrational. [Hint: To show that x=1+√3 is irrational, form the equivalent equations x−1=√3, (x−1)2=3, and x2−2x−2=0 and show that the last equation has no rational roots.]
√3
3√4
3−√2
(9)23
In Exercises 91–102, find a polynomial equation of least possible degree with integer coefficient whose roots include the given numbers. Use the result: If an equation with integer coefficients has a root (a+√b) where a and b are rational but √b is irrational, then the equation also has the root (a−√b).
1, −1,0
2, 1, −2
−12,2,73
−13, −12,16
1+√2,3
3−√5,2
1+√3,3−√2
2−√5,2+√3
√2+√3
2+√3+√5
3−√2+√5
√2+√3+√5
To prove the rational zeros test, we assume the Fundamental Theorem of Arithmetic, which states that every integer has a unique prime factorization. Supply reasons for each step in the following proof.
F(pq)=0, and pq is in lowest terms.
an(pq)n+an−1(pq)n−1+⋯+a1(pq)+a0=0
anpn+an−1pn−1q+⋯+a1pqn−1+a0qn=0
anpn+an−1pn−1q+⋯+a1pqn−1=−a0qn
p is a factor of the left side of (iv).
p is a factor of −a0qn.
p is a factor of a0.
an−1pn−1q+⋯+a1pqn−1+a0qn=−anpn
q is a factor of the left side of the equation in (viii).
q is a factor of −anpn.
q is a factor of an.
Find all rational roots of the equation
2x4+2x3+12x2+2x−32=0.[Hint: Multiply both sides of the equation by the lowest common denominator of the coefficients.]
Critical Thinking / Discussion / Writing
True or False.
13 is a possible zero of P(x)=x5−3x2+x+3.
25 is a possible zero of P(x)=2x7−5x4−17x+25.
Find all the zeros of f(x)=x4−2x3−4x2+4x+4, if one of its zeros is √2.
[Hint: f(x) has integer coefficients, so −√2 is also a zero.]
Getting Ready for the Next Section
In Exercises 107–116, simplify each expression.
(−2i)5
(x+i)(x−i)
(2x+i)(−2x+i)
(x+3i)(x−3i)
(5x+2i)(5x−2i)
(2x+8i)(x−4i)
(x−1+2i)(x−1−2i)
[x−(3−i)][x−(3+i)]
[x−(2+3i)][x−(2−3i)]
[x−(1+√3i)][x−(1−√3i)]
