APPENDIX A
Deriving the Rule of Thumb

The rule of thumb for calculating the rate of drift in Eurodollar rates relative to forward rates stems directly from calculating the expected gain when a forward swap is hedged with Eurodollar futures and applying the “no free lunch” principle.

SWAP VALUE

The net present value of a forward swap that receives fixed and pays floating for a 3-month period is:

where

NPA is the swap’s notional principal amount
X is the fixed rate at which the swap is struck
F is the forward rate

Days is the actual number of days in the swap period to which the floating and fixed rates apply

Z is the fractional price of a zero-coupon bond that matures on the swap payment date (which is Days following the swap rate setting date)

The interest rates in this expression are expressed in percent (that is, 7 percent would be 0.07). If we multiply and divide this expression by $1,000,000 as well as by 90, we get

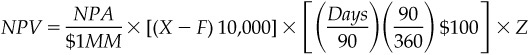
which is fairly messy but allows us to arrive at

in which X^* and F^* are expressed in basis points. We also find the $25, which corresponds nicely to the value of a tick or basis point on a Eurodollar futures contract. The value of Days/90 compensates for the actual length of the swap period.

When a typical swap is transacted, we begin with X^* = F^* so that the net present value of the swap is zero. When interest rates change, both F^* and Z change, and both contribute to the swap’s profit or loss.

SWAP P/L AND HEDGE RATIO

For a change of ΔF^* in the forward rate and ΔZ in the price of the zero, the profit on the forward swap is

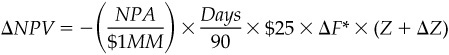
Because the change in the value of one Eurodollar futures contract is equal to −$25 × ΔF*, the number of futures contracts needed to hedge against unexpected changes in rates would be

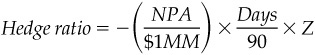
This hedge ratio makes sense. The minus sign indicates that the hedger must short the contracts, NPA/$1MM captures the nominal number of contracts required, Days/90 reflects the importance of the day count in the swap, and Z provides the present value correction for the difference in timing of the cash flows on the futures and the swap.

EURODOLLAR P/L

Given this hedge ratio, the profit on the short Eurodollar futures position would be

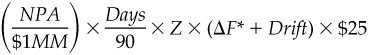
where Drift represents the systematic change in the Eurodollar futures rate relative to the forward rate needed to compensate for the convexity difference between the swap and the futures contract.

EXPECTED HEDGE P/L

To eliminate any possibility of a free lunch in this hedge, the expected profit of the hedged swap must be zero. Put differently, the expected profit on the swap must exactly offset the expected profit on the Eurodollar position. Because the [(NPA/$1MM) × (Days/90) × $25] is common to both the profit on the swap and the profit on the Eurodollar position, this part of both expressions cancels out. The result of setting the two combined profits equal to zero and rearranging shows us that

E[ΔF^* × (Z + ΔZ)] = E[Z × (ΔF^* + Drift)]

where E[] represents the market’s expectation today of whatever is contained inside the brackets. Because Z is a known number, we can solve for the drift by dividing through by Z within the expectations to get

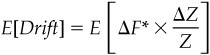
If we combine this expression with the fact that the average move in forward rates and term rates will be zero and use the formula for correlation, we arrive at the rule of thumb:

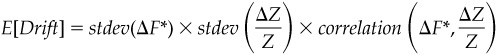
This rule of thumb assumes nothing, by the way, about the distribution of rate changes.

PRACTICAL CONSIDERATIONS

• The drift is expressed in basis points per period if the standard deviation of ΔF^* is in basis points per period.

• To use volatilities from the options market, relative or percentage rate volatilities must be converted to absolute rate volatilities by multiplying by the level of the interest rate.

• ΔZ/Z is the unexpected return on a zero-coupon bond over the period. It should be expressed as a fraction (for example, as 0.015). The easiest way to compute the standard deviation of ΔZ/Z is to break it into two parts: the standard deviation of the zero’s continuously compounded yield and duration. (See Appendix B for the method used to compute continuously compounded zero-coupon yields from Eurodollar futures rates.)

• The length of the period over which you calculate changes in rates is not terribly important as long as the duration for the zero-coupon bond is chosen to be its average years to maturity over the period. A period of one day would be theoretically correct, because mark-to-market actually occurs daily in the futures market. But this would be computational overkill. Using a quarterly period produces almost the same result as daily calculations but involves a lot less work.