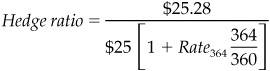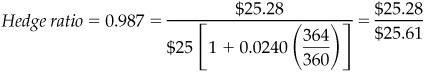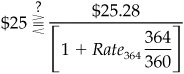CHAPTER 5
Hedging with Eurodollar Futures

Hedging and replicating are two sides of the same coin. You may have this sense already, but you will find in this chapter that you can use a Eurodollar futures contract to convert a floating rate asset (or liability) into the equivalent of a fixed rate asset (or liability). Or you can convert a fixed rate asset into a floating rate asset.

In the one case—when you are converting a floating rate asset into a fixed rate asset—what you are really doing is hedging a forward cash flow. That is, you are fixing the amount of cash that will show up on some future date. Whether you think of this as cash flow hedging or as replicating future or forward cash flows is perfectly fine as long as your objective is clear.

In the other case—when you are turning a fixed rate asset into a floater—what you are really doing is fixing the present value of your position. And while protecting the present value of your position against changes in interest rates may sound more like hedging in the traditional sense, it is really only one way of thinking of it.

One thing is clear. If you hedge a forward cash flow, the present value of your position will vary with the level of interest rates. But if you hedge the present value of your position, your forward cash flows will vary with the level of interest rates. Thus, you can hedge cash flows, or you can hedge present values, but you cannot do both at the same time. Or what is the same thing, you can convert floating to fixed or fixed to floating, but not both at the same time.

Once we know what we want to do, the challenge is to do it correctly. The purpose of this chapter is to show how to reckon Eurodollar futures hedge ratios and how to manage the hedges over time.

In this chapter, we will work both with cash flow hedging and with present value hedging. In particular, we will show how to:

• Calculate zero-coupon bond prices from Eurodollar rates

• Convert a floating rate note into a fixed rate note

• Calculate the correct number of Eurodollar futures needed for a hedge

• Hedge the present value of a fixed rate instrument

• Manage a Eurodollar hedge over time

• Work with real-world complications

THE TOOL IS A EURODOLLAR FUTURES CONTRACT

Henry Ford’s line about the customer being able to have a model T in any color he wanted as long as it was black is apt here. Our hedging tool is the Eurodollar futures contract. For hedging purposes, the contract has three important features that determine completely the way we have to use the tool. First, the value of the contract is determined by the value of a 3-month interest rate that spans the period covered by the contract (e.g., from March 19, 2003, to June 18, 2003, for the March ′03 contract). Second, each basis point change in the underlying interest rate is worth $25. And third, because gains and losses on futures are settled every day in cash, the present value of the gain or loss is also $25.

BASIC HEDGE ALGEBRA

As a result of this structure, every hedging problem works the same way. We want a number of futures contracts whose change in value, for a given change in an underlying interest rate, will equal any change in the value of what we are trying to hedge or replicate. When using Eurodollar futures, we begin by isolating the effect of a change in the 3-month rate underlying a particular futures contract on what we want to hedge. We then divide this value by the change in the value of the Eurodollar futures contract. That is, once we have determined how much a change in any given Eurodollar futures rate will affect the value of our position, we calculate the hedge ratio as shown in Equation 5.1.

EQUATION 5.1
Hedge Ratio

And, depending on whether the change in the value of the position is a forward value or a present value, the hedge ratio can be written, for a 1-basis-point change in the underlying 3-month futures rate, as shown in Equation 5.2 or Equation 5.3.

EQUATION 5.2
Hedge Ratio for Forward Values

EQUATION 5.3
Hedge Ratio for Present Values

The sign of the hedge ratio depends, of course, on whether you want to offset or replicate a change in value.

DERIVING PRESENT AND FORWARD VALUES FROM EURODOLLAR FUTURES RATES

Sooner or later, cash today must be translated into cash tomorrow, or cash tomorrow must be translated into cash today. Eurodollar futures not only allow us to do this, but provide us with information about the rates at which these conversions can be made.

Calculating a Forward Value (Terminal Wealth)

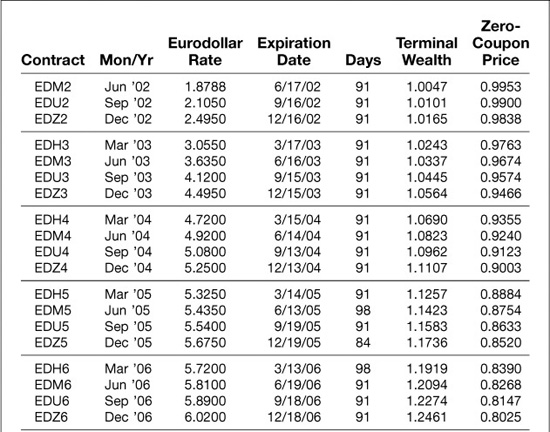
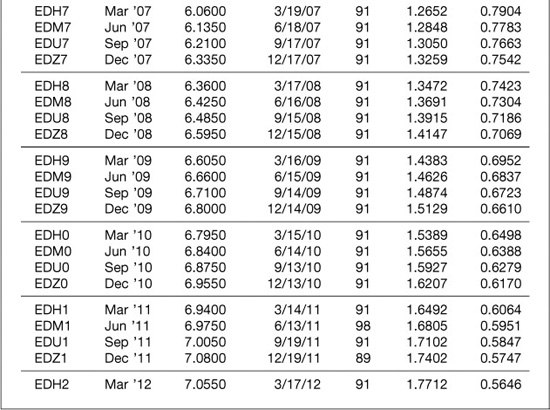
Consider Exhibit 5.1, which provides Eurodollar futures rates for all 40 contracts as of the expiration of the June ′02 contract on June 17, 2002. The exhibit also shows the actual number of days between futures expirations for each contract. From these rates and days, we can determine how much $1, if invested at the sequence of Eurodollar rates implied by the futures contracts, would produce at the end of any given 3-month period. For example, $1 invested on June 17, 2002 (value date June 19, 2002) for 91 days would produce $1.0047 [= $1 × (1 + 0.018788 × (91/360))]. If this entire amount were rolled over at the next rate of 2.105% for the next 91 days, the result would be $1.0101 [= $1.0047 × (1 + 0.02105 × (91/360))], and so forth. The results of these calculations are shown in the column labeled Terminal wealth. Equation 5.4 shows the calculation of terminal wealth.

EXHIBIT 5.1
Terminal Wealths and Zero-Coupon Bond Prices June 17, 2002

EQUATION 5.4
Calculate Terminal Wealth Using Futures Rates

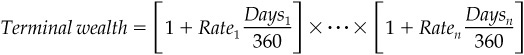
where

Terminal wealth is the maturity value of $1

             Rate is the interest rate for the spot or forward period

             Days is the number of days in the interest rate period

                   n is the forward period

Calculating a Zero-Coupon Bond Price (Present Value)

The inverses of these terminal wealth values represent the prices of LIBOR-based zero-coupon bonds that mature on the respective dates (see Equation 5.5). For example, since $1 invested today would produce $1.0243 1 year from now, one need pay only $0.9763 [= 1/$1.0243] for a bond that would pay $1 dollar 1 year from now.

EQUATION 5.5
Calculate the Zero-Coupon Bond Price

where

m is the number of days to maturity

HEDGING OR REPLICATING FORWARD CASH FLOWS

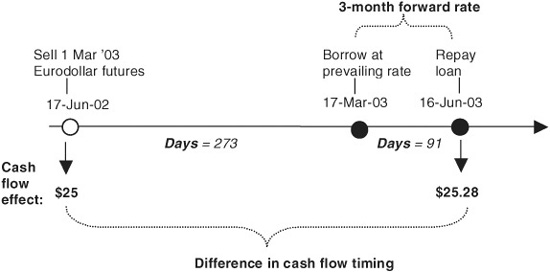
Much of the work in the world of applied finance is making certain amounts of money show up on certain days in the future. You have money today that must be converted into a different amount of money sometime later. With this in mind, consider the task of converting a 3-month floating rate liability, 9 months forward, into a fixed rate liability. That is, consider the problem of converting a floating rate note into a fixed rate note.

EXAMPLE 5.1

Forward Valuing the Gain or Loss on the Eurodollar Futures Contract

Suppose you are short 1 March ′03 Eurodollar futures contract and that the March ′03 rate rises 1 basis point. You have a $25 gain today on your futures position and a $25.28 loss 1 year from now on your floating rate loan. To know whether 1 Eurodollar futures contract is the right hedge for this position, you need to know whether $25 today is more than you need, just enough, or less than you need to cover your $25.28 loss 1 year hence.

EXAMPLE 5.2

Present Valuing the Gain or Loss on a Floater

The big advantage of approaching the hedging problem by forward valuing the $25 per basis point on a Eurodollar futures contract is that it highlights the true hedging or replicating problem. Futures contracts either pay or take away cash on a daily basis. If you receive money, you must invest it until you need it. If you pay money, you must finance your payments until you have the cash to pay it off.

The big disadvantage of using forward values is that there are an infinite number of forward dates to handle.

EXAMPLE 5.3

The chief advantage of using present values rather than forward values is that there is a single present date, which is a great analytical simplification. The big drawback, of course, is that present values obscure the realities of forward cash flow management. So take your pick.

HEDGING OR REPLICATING PRESENT VALUES OF CASH FLOWS

If the forward cash flow is fixed, hedging becomes a problem of offsetting changes in the cash flow’s present value. And if we do this, we will succeed in converting a fixed rate note into a floating rate note.

Calculating the Price of a Zero-Coupon Bond

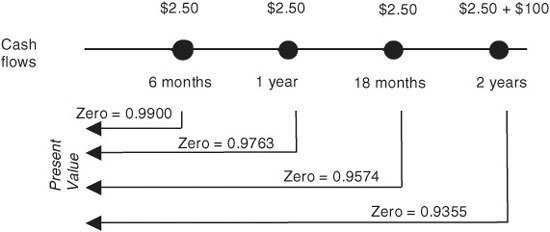
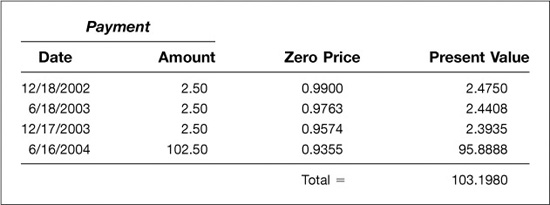
Suppose you hold a $100,000,000 1-year zero-coupon bond issued by someone with LIBOR quality credit. Because the credit quality of the issue is the same as the credit quality implied by Eurodollar futures rates, the present value of this zero would be $100,000,000 times the price of a 1-year Eurodollar zero. From Exhibit 5.1, we find that this price is a function of four Eurodollar rates and can be written as

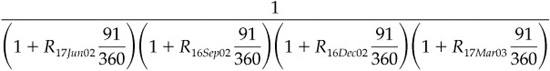
Given rates of 1.8788%, 2.105%, 2.495%, and 3.055%, the price of a 1-year Eurodollar zero would be $0.9763, and the present value of your $100 million zero would be $97,630,000.

Calculating the Present Value of a Basis Point

Once you have determined the value of your zero-coupon bond, the next step is to determine how much the value of your bond will change if any of the four rates that determine the price of the zero change 1 basis point. The results of increasing and decreasing each of the four rates (while holding the other three fixed at their original values) are shown in Exhibit 5.2. In all cases, the zero-coupon bond prices are calculated to 10 decimal places so that changes in the value of a $100 million zero-coupon bond could be determined to the nearest cent.

EXHIBIT 5.2
Effect of Rate Changes on the Value of the $100 Million 1–Year Zero

Consider, for example, a change in the Jun ′02 rate. If this rate were to increase by 1 basis point, the price of the 1-year zero would fall from 0.9762617812 to 0.9762372207, a decrease of 0.0000245605, which would be worth $2,456.05 for a $100 million zero. If this same rate were to decrease by 1 basis point, we see that the zero price would increase to 0.9762863429, an increase of 0.0000245617, which would be worth $2,456.17. The difference in the size of the effect reflects what is known in fixed income markets as “positive convexity,” which describes the fact that the bond’s price will increase more as rates fall than it will decrease as rates rise.

Finding the Hedge for a Zero-Coupon Bond

When hedging the position, of course, you do not know which way rates will go, so you average the two results, which would produce an average change in position value of $2,456.11. To hedge this exposure, one would sell 98.24 [= $2,456.11/$25.00] of the Jun ′02 contract to hedge a long position or buy 98.24 contracts to replicate the behavior of a long position.

The results for the other three contracts are very nearly the same. They differ from one another only because of the slight upward slope in the Eurodollar futures rate curve. Effects of a change in the Mar ′03 rate are multiplied by a slightly smaller number (because the rates at the front of the curve are lower) than are the effects of changes in the Jun ′02 rate (because the rates at the back of the curve are higher). If the four Eurodollar rates were identical, the resulting hedges would be identical, too.

Faster Hedge Ratio Calculations with Calculus

The advantage of reckoning the effects of rate changes up and down is that you can see the actual changes in position value. Because your hedges are averages of the effects of both increases and decreases in rates, however, you can find your hedge ratios faster, with less computing time, if you use calculus.

The price of any given zero-coupon bond is simply a function of a string of spot and Eurodollar futures rates, and the partial derivative of this function with respect to any one of those rates allows us to calculate hedge ratios quickly and accurately.

We begin with Equation 5.6, which shows the price of a zero that matures n quarters from now. We then use partial derivatives, as shown in Equation 5.7, to express the effect of a change in any one of the sequence of rates (e.g., the ith rate) on the zero’s price.

EQUATION 5.6
Calculate the Zero-Coupon Bond Price

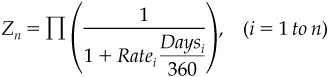
where

    Z_n is the zero-coupon bond price at time n

Rate_i is the interest rate for the spot or forward period i

Days_i is the number of days in the interest rate period i

∏ is the mathematical symbol for taking the product of the term that follows it over a specified range, in this case from 1 to n

EQUATION 5.7
Calculate a Hedge Ratio Using Calculus

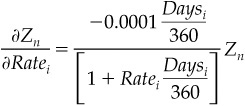
where

σZ_n/σRate_i is the change in the zero-coupon bond price given a change in the ith period rate

As long as we get the units right when we plug in the key values, this will give us what we need to calculate the correct hedge ratio. Consider a change in the June ′02 rate on the price of the 1-year (4-quarter) zero in the example above. The original zero price is 0.9762617812, so the partial effect of a change in the June ′02 rate would be

which, if multiplied by a $100,000,000 principal amount, would produce a total dollar effect of $2,456.11.

Pricing and Hedging a Coupon-Bearing Bond

Once you know how to price and hedge a zero-coupon bond, you will have no trouble pricing and hedging coupon bearing bonds, which are simply packages of zero-coupon bonds.

EXAMPLE 5.4

Finding the appropriate hedge for this bond requires nothing more than finding the correct hedges for each of the four cash flows and then adding them up. Using the hedge ratio formula derived in the previous section, we can calculate the number of Eurodollar futures needed to hedge $1 million par amount of zeros with maturities of December 18, 2002, June 18, 2003, December 17, 2003, and June 16, 2004. The results of these calculations are shown in Exhibit 5.4.

EXHIBIT 5.4
Number of Eurodollar Futures Needed to Hedge $1 Million Par Amount Zero
June 17, 2002

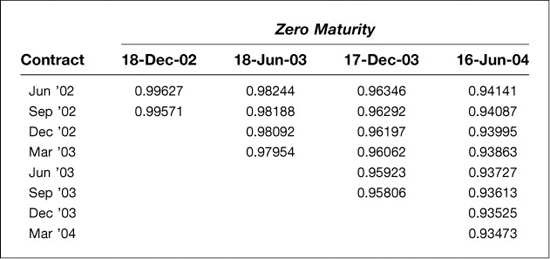
For example, to hedge $1 million of a zero that matures on December 18, 2002, we would have to sell 0.996 of the Jun ′02 and Sep ′02 contracts (see upper panel of Exhibit 5.4). As a result, to hedge the first coupon payment of $2.5 million that arrives on

Number of Eurodollar Futures Needed to Hedge $100 Million Par Amount 5% Semiannual Coupon Bond
June 17, 2002

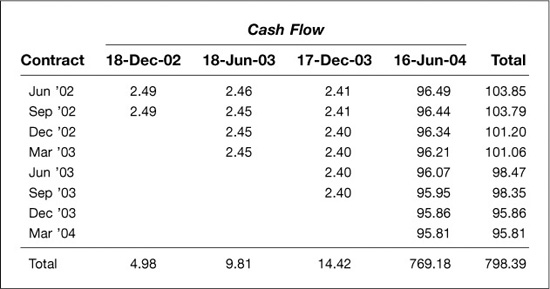
December 18, we would have to sell 2.49 of each (see lower panel of Exhibit 5.4). To hedge $1 million of a zero that matures on June 18, 2003, we would have to sell 0.982, 0.982, 0.981, and 0.980 of the Jun ′02, Dec ′02, Mar ′03, and Jun ′03 contracts respectively. To hedge the second semiannual coupon payment, then, we would have to sell 2.46, 2.45, 2.45, and 2.45 of each of these contracts. And so forth.

This example serves at least two useful purposes. First, it highlights the subtle but important effect of cash flow timing on hedge ratios. More distant cash flows require smaller hedge ratios because their present values are lower.

Second, it highlights an important feature of coupon-bearing bonds that might not otherwise be apparent. That is, the price of a coupon-bearing bond is relatively more sensitive to changes in near term forward rates than is the price of a zero-coupon bond with the same final maturity. A change in the Jun ′02 or Sep ′02 Eurodollar rates will affect the present value of four separate cash flows on a coupon-bearing bond, while a change in the Dec ′03 or Mar ′04 rates will affect the present value of only the final cash flow. With a zero, changes in these four contract rates would have nearly identical effects on the price because there is only one, final, cash flow. As a result, the Eurodollar hedge for a coupon-bearing bond will place greater weight on the nearby contract months (e.g., 103.85 of the June ′02 contract) than on later contracts (e.g., 95.81 of the March ′04 contract).

MANAGING HEDGE RATIOS

Eurodollar futures hedges are not static. We can see from the hedging problems we have solved in this chapter that our hedges will change as interest rates rise or fall and as time passes.

As Rates Rise or Fall

As interest rates fall, the prices of non-callable bonds become more sensitive to changes in interest rates while Eurodollar futures prices do not. As interest rates rise, non-callable bond prices become less sensitive to yield changes, while the present value of a basis point on a Eurodollar contract remains $25. Thus, Eurodollar hedge ratios for non-callable bonds will tend to increase as interest rates fall and to decrease as interest rates rise.

If you are hedging a long position in a non-callable bond (or are receiving fixed in an interest rate swap, which we consider in the next chapter), you will welcome these kinds of adjustments. Decreases in interest rates will require you to sell more Eurodollar futures, while increases in interest rates will require you to buy back some of your futures. Since these kinds of adjustments automatically prompt you to sell when prices have gone up and to buy when prices have gone down, you will find yourself making money on average with these adjustments. This advantage to being short Eurodollar futures when hedging bonds that possess positive convexity has important implications for the pricing of Eurodollar futures. The question of what this advantage is worth and the effect it has on Eurodollar futures prices is the subject of “The Convexity Bias in Eurodollar Futures,” chapter 7.

As Time Passes

Because present values tend to rise with the passing of time, Eurodollar hedge ratios tend to rise as well. Consider the problem of converting a floating rate borrowing into a fixed rate borrowing.

Exhibit 5.5 shows how many Eurodollar contracts are needed to convert a 3-month floater into a 3-month fixed rate note at forward horizons ranging from 3 to 21 months (and final loan maturities ranging from 6 to 24 months). In each case the nominal forward value of a basis point on the borrowing is $2,527.78 for a $100 million note with a 91-day maturity, but the present value of a basis point change in the borrowing rate is higher for nearer forward periods. For example, if you plan to initiate the forward borrowing in March 2003 (as the problem was originally cast), the loan would mature in June 2003, and the present value of the $2,527.78 nominal basis point value would be $2,467.78. To hedge this would require 98.7 contracts. On the other hand, if you plan to initiate the borrowing in March 2004 and pay it back in June 2004, the present value of the $2,257.78 would be $2,364.70, and the Eurodollar hedge would be 94.6 contracts.

EXHIBIT 5.5
Number of Eurodollar Futures Needed to Hedge the Cost of Borrowing $100 Million for 91 Days
June 17, 2002

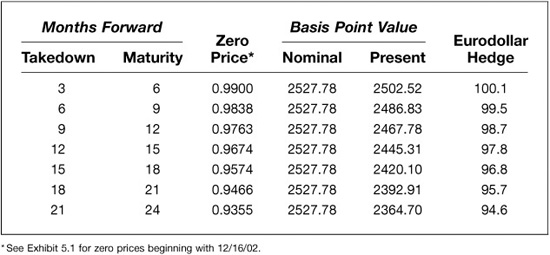
An important implication of this result is that the number of futures needed to hedge a March 2003 forward borrowing would increase with the passing of time. In this example, you would have to add roughly 1 contract per quarter to your hedge. Such an effect is almost glacially slow, but in practice, the effect is large enough to make a difference if the book you are hedging is large enough. Banks that manage several hundreds of billions of dollars of assets and liabilities will find their hedge ratios changing every day.

While such day-to-day adjustments might seem to be a nuisance, the transaction economics of the futures industry is particularly well suited to this kind of fine tuning. For an active participant in the Eurodollar market, the cost of trading 1 contract is simply 1/100th the cost of trading 100 contracts. As a result, the hedger can make small adjustments to his position without incurring unduly large costs.

PRACTICAL CONSIDERATIONS IN REAL HEDGES

In any real hedging problem, you will come up against several gaps and misalignments. For one thing, you will find that you have exposure to a spot interest rate—called the stub rate—that spans the period from today until the first available Eurodollar futures expiration. For another, your own interest rate exposure almost certainly will not line up with the terms covered by Eurodollar futures. And for yet another, the rate at which you will borrow or lend will be done at what is now an unknown spread against LIBOR. All of which suggests that anyone who hedges with Eurodollar futures has to be willing to live with a certain amount of unhedgeable risk or to bring other hedging tools to bear.

The Stub Period

Every pricing and hedging problem with futures must deal with the stub period—the time that separates us from the first available Eurodollar futures contract expiration. In the examples so far in this chapter, we have assumed that the June ′02 contract was still available for trading or hedging. As a practical matter, though, we will find ourselves with several days or weeks between us and the first available contract.

For example, when the June ′02 contract expires, the next contract available in the quarterly contract cycle is the Sep ′02 contract. When that happens, we find that the value of our position may depend on the 3-month rate from the middle of June until the middle of September, but that we have no obvious futures tool for dealing with the risk. Our stub period in this case would be 3 months long, and the stub rate would be a 3-month cash market rate.

The stub period shrinks with the passing of time, of course. By the middle of July, the stub period would have shrunk to 2 months, and the stub rate would be a 2-month cash rate. By the middle of August, our exposure would be to a 1-month cash rate.

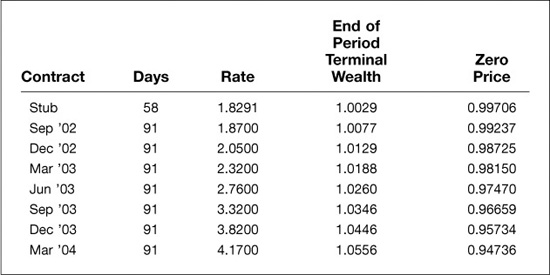
The stub period poses two problems—one for pricing and one for hedging. The pricing problem is not especially difficult to solve. All we need, instead of a futures rate, is an appropriate term value for LIBOR with which we can begin the process of calculating terminal wealths and zero-coupon bond prices. In Exhibit 5.6, which reflects the market as of the close of business on Thursday, July 18, 2002, we found a cash stub rate of 1.8291 percent. The value date for any cash market transaction on Thursday would be the following Monday, July 22. With a value date of September 18 for the rate to which the Sep ′02 futures contract will settle, this stub rate covered 58 actual days. As a result, terminal wealth for the end of the stub period was 1.0029 [= 1 + 0.018291 × (58/360)], which we assume can be rolled over at the rate of 1.87% that was implied by the price of the Sep ′02 Eurodollar contract at the close of business on July 18.

EXHIBIT 5.6
Constructing Terminal Wealths and Zero Prices Using a Stub Rate
Trade Date = Thursday, July 18, 2002
Value Date for Stub Rate = Monday, July 22, 2002

The hedging problem posed by the stub rate is more difficult to solve. Changes in stub rates tend to exhibit a low correlation with changes in Eurodollar futures rates as shown in Exhibit 5.7.

EXHIBIT 5.7
Correlation between Weekly Changes in Lead Eurodollar Futures Rates and Spot LIBOR
January 1997 through July 2002

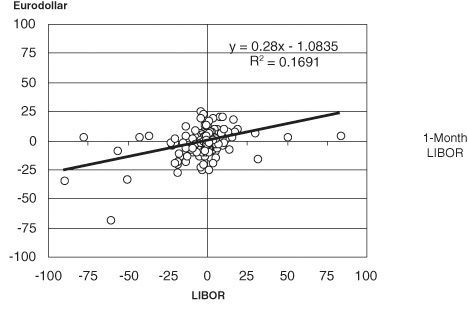
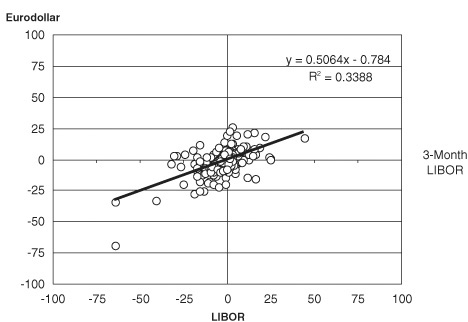
This leaves the hedger with three choices. One is to leave the risk unhedged. Part of the reason for the low correlation between changes in stub rates and changes in the first Eurodollar contract rate is that Fed policy has a very powerful influence over short-term money markets. It is possible for 1-month and 2-month deposit rates to be very stable for long stretches of time. So it is possible for a well-informed hedger to take a considered risk and leave the exposure unhedged.

If the hedger wants to do something about the exposure, though, there are really just two choices. One is to effect a cash market transaction—for example, borrow cash for 58 days in this example at a term money market rate—or piece together a strip of Fed funds futures, which because of the way they settle, tend to provide excellent hedges for very short-term money market exposure.

Date and Term Mismatches

The interest rate that represents the source of your risk almost never will correspond exactly to the 3-month forward rate periods defined by the expirations of Eurodollar futures. The rate you care about typically will have a maturity other than 3 months, and the period spanned by your rate will begin and end on dates that do not line up with Eurodollar expirations.

Consider, for example, a problem in which the source of your risk is a 6-month rate that begins 1 month before the expiration of the Dec ′02 contract and ends 2 months after the expiration of the March ′03 contract. The links between this rate and the relevant Eurodollar futures rates is illustrated in Exhibit 5.8. In this exhibit, we show the terminal wealths that could be calculated from known stub and Eurodollar futures rates on July 18, 2002. We also show interpolated values of terminal wealths for the start and end dates of your 6-month period.

EXHIBIT 5.8
Interpolating Terminal Wealths
July 18, 2002

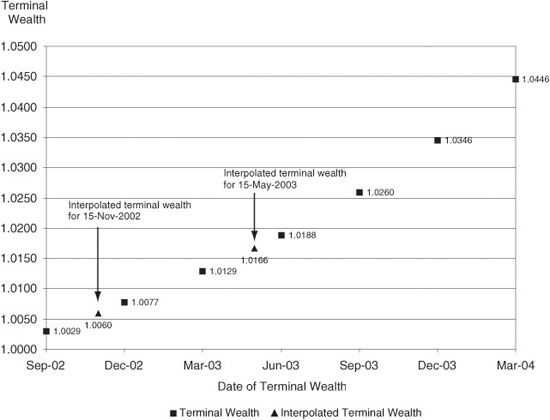
From these interpolated terminal wealths (TW), we can derive the implied forward rate we care about. The forward-starting 6-month rate is 2.10%.

The logical linkage, then, between changes in Eurodollar rates and changes in the rate that is the source of our risk, requires a reliable interpolation routine. For a wide range of hedging problems, we use linear interpolations of the natural logs of known terminals wealths. Just how this is done, along with pros and cons, is described in “Measuring and Trading Term TED Spreads,” chapter 11.

Whole Contracts

In this chapter, we have shown several decimal places when reporting the results of hedge ratio calculations. The decimals are important because the effects of time and the level of interest rates can be subtle and hidden by rounding. At the same time, when you actually want to hedge something, you are constrained to transact in whole numbers of contracts. As a result, you must buy or sell either more or less than specified by the exact hedge ratio. To some extent, you can smooth things out by slightly under-weighting one contract month and slightly overweighting a neighboring contract. Also, the whole contract problem becomes relatively less important as the size of the position you are hedging increases.

Credit Spreads

The U.S. Treasury has a better credit standing than do LIBOR quality banks. As a result, if you value a Treasury bond using Eurodollar zero prices, the present value produced by this approach would be lower than the bond’s price. On the other hand, if we were valuing a junk bond, the present value produced by this approach would be higher than the bond’s price.

If you plan to use futures to value or hedge bonds with credits that are either better or worse than the credit that underpins the LIBOR market, you need a way to determine the credit spread between the two markets. You also must be careful to work with the correct bond price when determining hedge ratios. Both of these problems are dealt with in detail in “Measuring and Trading Term TED Spreads,” chapter 11. This chapter also contains a highly detailed technical appendix that covers problems of date mismatches and differences in day-count conventions that will be useful to anyone who has to do the coding for in-house computer programs.

Variable Credit Spreads

While the Eurodollar contract is tied to LIBOR, almost no one—with the exception of A1/P1 rated banks—actually borrows or lends at LIBOR. Almost all transactions will be done at a spread either above or below LIBOR, and the spread can vary, sometimes a lot. Changes in the spread are perhaps more important for borrowers than for lenders and a careful consideration of your own credit situation can play an important role in whether you decide to use Eurodollar futures to hedge. For example, if you have excellent credit but face the possibility of a worsening of your credit, you might well prefer to lock in your financing rates in the term financing market rather than borrowing at floating rates and using Eurodollar futures to cover your floating rate exposure. Eurodollar futures will protect you against changes in LIBOR but will afford no protection against a worsening of your own spread against LIBOR. In contrast, if your credit is already bad but may improve, you might better your financing costs by using futures to cover your variable rate exposure and leave yourself open to enjoying the benefit of a fall in your own financing rate relative to LIBOR.