4.6. Qualitative Reasoning
An exactly quantitative description of the world being analyzed is not always available. For example, in the early stage of engineering design of a device, one may not know the exact value of all parameters of the device. In this case the incomplete knowledge can be used by representing the device in a qualitative form. By using the qualitative description we can get a better understanding of the device at the desired level. A reasoning based on the qualitative description of the world is called qualitative reasoning. The device’s behaviors can be predicted and the decisions can be made using the reasoning. Therefore, qualitative reasoning is to provide a broad picture of the functioning of the world by taking a step back from the detail. There is a great deal of interest in developing such techniques both by engineers and AI researchers.
In this section, the representation of qualitative reasoning in our multi-granular world model and its reasoning procedure are discussed.
4.6.1. Qualitative Reasoning Models
In common sense, if we say, ‘Someone is 185 cm tall’, it is regarded as a quantitative representation by describing an attribute with numbers. If we just say, ‘Someone is tall’, this is just a qualitative representation. In professional fields, for example, for a differential equation, if an analytical or a numerical solution is required, it needs a quantitative analysis. Meanwhile, only the existence and the properties of the solution are desired, it only needs a qualitative analysis. Qualitative analysis is widespread not only in common sense but also in professional fields.
In AI, researchers have been paying close attention to qualitative description and reasoning recently. They proposed several new fields such as qualitative physics, mechanics, etc. In these fields, people do not seek the precise solution of the problems but only the qualitative variation or variation trend of physical quantities is concerned.
In fact, ‘Tall’ is an uncertain description of ‘185 cm’ height of a person. A qualitative description of a variable is just a coarse-grained description of the variable with real number. Therefore, qualitative reasoning can be represented by a multi-granular world model. However, reasoning on some quotient space may be regarded as ‘quantitative’. But it may also be considered as ‘qualitative’ when the more precise analysis is required and vice versa. Therefore, quantitative and qualitative are relative.
Qualitative reasoning is the reasoning with qualitative representation. From the above observations, it is known that the projection and synthetic approaches of quotient spaces presented in the previous chapters can be applied to qualitative reasoning.
4.6.2. Examples
Example 4.20
Williams (1988) presented a so-called qualitative algebraic reasoning that mixes qualitative with quantitative information. His approach is briefly introduced below.
Let 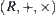 be real with operators ‘+’ and ‘×’. Let
be real with operators ‘+’ and ‘×’. Let 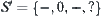 be a qualitative algebra with operators
be a qualitative algebra with operators 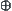 and
and 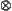 shown below.
shown below.

A unary operator ⊝ is defined as

Define a projection 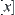 :
: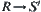 as
as
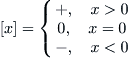
Element ‘?’ corresponds to the entire real axis 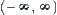 .
.
Qualitative algebra 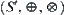 has the following properties.
has the following properties.
Associative Law:
![]()
Identity Element:
![]()
Commutative Law:
![]()
Distributive Law:
![]()
An integral power of element s is defined as 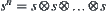 , where n is an integer.
, where n is an integer.
Williams constructed a qualitative reasoning system with numbers based on hybrid algebra 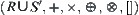 . Its reasoning procedure is the following.
. Its reasoning procedure is the following.
(1) An equation with real number is simplified based on space 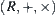 .
.
(2) The simplified equation is projected on space 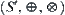 .
.
(3) Then, the projected equation is operated using qualitative operators on space 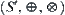 .
.
The advantage of the above qualitative reasoning procedure is the following. If the sign of some quantities is known rather than the precise value, the quantities cannot be operated on real space R using standard real operators. But they can be operated on 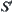 using qualitative operators. Moreover, since on
using qualitative operators. Moreover, since on 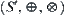 for any element t,
for any element t, 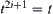 , any polynomial can be transformed into a quadratic polynomial. This is a specific property that does not occur in real space R. But the weakness of operation on
, any polynomial can be transformed into a quadratic polynomial. This is a specific property that does not occur in real space R. But the weakness of operation on 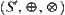 is that the projection of
is that the projection of 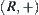 on
on 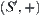 is not homomorphism. In our terms, it means that operator
is not homomorphism. In our terms, it means that operator 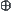 is not a quotient operation of
is not a quotient operation of 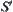 , i.e., the operation
, i.e., the operation 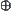 on space
on space 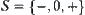 does not necessarily have a unique result. For example,
does not necessarily have a unique result. For example, 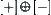 does not have a unique result on S.
does not have a unique result on S.
Now, we analyze Williams’s hybrid algebra from the multi-granular computing viewpoint (Zhang and Zhang, 1989c, 1990b).
Let 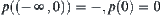 and
and 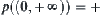 . Therefore,
. Therefore, 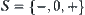 is a quotient space of
is a quotient space of 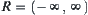 . p is a projection from R to S. Operators
. p is a projection from R to S. Operators  and
and 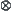 of S are the projections of operators
of S are the projections of operators 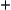 and
and  of R, respectively.
of R, respectively.
It is easy to know that operator  is a quotient operation of S but
is a quotient operation of S but 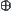 is not. As stated before, the upper bound space of S with respect to operator
is not. As stated before, the upper bound space of S with respect to operator 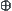 is R itself.
is R itself.
Thus, in our terms, Williams’s qualitative reasoning with numbers is a reasoning on quotient space S with respect to the projections of operators 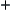 and
and  . Since
. Since 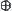 is not a quotient operator on S, in order to get a unique result from the operation, the approximate approach for finding upper bound space as shown in the above section can be used for solving the problem.
is not a quotient operator on S, in order to get a unique result from the operation, the approximate approach for finding upper bound space as shown in the above section can be used for solving the problem.
Example 4.21
Murthy (1988) presented a qualitative reasoning at multiple resolutions. We briefly introduce this as follows.
(1) 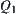 space denoted by
space denoted by 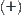
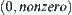 is identical to S={-,0,+}.
is identical to S={-,0,+}.
The relationships  between quantities on
between quantities on 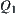 can be expressed as follows.
can be expressed as follows.
If 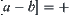 , then
, then 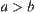 . If
. If 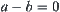 , then
, then 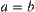 . If
. If 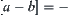 , then
, then 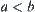 .
.
Where 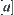 denotes the sign of a.
denotes the sign of a.
It is noted that if 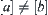 and a and b have different signs, then
and a and b have different signs, then 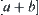 is uncertain. This ambiguity can be solved by moving to the next
is uncertain. This ambiguity can be solved by moving to the next 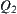 space.
space.
(2) 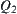 space is denoted by
space is denoted by 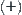 (0, infinitesimality, large).
(0, infinitesimality, large).
Refining 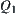 space, first interval
space, first interval 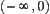 is divided into
is divided into 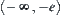 and
and 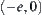 , then interval
, then interval 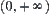 is divided into
is divided into 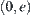 and
and 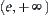 . Interval
. Interval 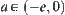 or
or 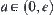 is called ‘infinimality’. Interval
is called ‘infinimality’. Interval 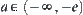 or
or 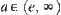 is said to be ‘large’. Therefore, on
is said to be ‘large’. Therefore, on 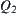 space in addition to relations
space in addition to relations 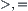 and
and 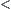 , the other two relations
, the other two relations 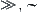 can be introduced as follows.
can be introduced as follows.
Relation 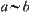 , if both a and b are infinitesimality or large.
, if both a and b are infinitesimality or large.
On 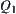 space, operations
space, operations 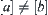 and
and 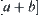 are ambiguity. But on
are ambiguity. But on 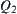 space, if a is large and b is infinitesimality, then
space, if a is large and b is infinitesimality, then 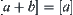 , i.e., the signs of
, i.e., the signs of 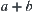 and a are the same. But if both a and b are infinitesimality or large, the sign of
and a are the same. But if both a and b are infinitesimality or large, the sign of 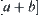 is still uncertain. These ambiguities can be solved by introducing
is still uncertain. These ambiguities can be solved by introducing 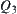 space.
space.
(3) 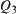 space is denoted by
space is denoted by 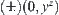 , where y is the base (e.g., 2 or 10 ) and z is an integer.
, where y is the base (e.g., 2 or 10 ) and z is an integer.
The real number is divided by the logarithmic distance between two numbers, i.e., if 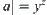 , then
, then 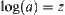 . Therefore, when
. Therefore, when 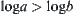 , then
, then 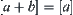 , in other words, when the order of magnitude of a is bigger than b, the orders of magnitude of a+b and a are the same. If
, in other words, when the order of magnitude of a is bigger than b, the orders of magnitude of a+b and a are the same. If 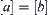 and
and 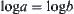 , then
, then 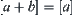 .
.
While  and
and 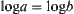 , the sign of
, the sign of 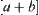 is uncertain. To resolve the ambiguity a finer resolution is needed. The
is uncertain. To resolve the ambiguity a finer resolution is needed. The 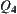 space is introduced.
space is introduced.
(4) 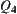 -space is denoted by
-space is denoted by 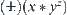 , where y and z as shown in (3) and x is a number with n significant digits. As n increases the accuracy of the description increases, while
, where y and z as shown in (3) and x is a number with n significant digits. As n increases the accuracy of the description increases, while 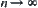 the Q-space approaches the real space R.
the Q-space approaches the real space R.
In order to solve the uncertainty of the sign of 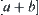 , Murthy gradually refines the Q-space so that the uncertainty of computational results reduces.
, Murthy gradually refines the Q-space so that the uncertainty of computational results reduces.
From the viewpoint presented in this book, Murthy’s Q-spaces of multiple resolutions are quotient spaces of real number at different granularities. The successive refinement approach presented by Murthy is just an approximation method for constructing an operational space of S = {-, 0, +} with respect to real addition. The approximation method for constructing operational space we presented can be used for general quotient space and any binary-operator. So the method can be applied to Murthy’s qualitative reasoning as well.
Example 4.22
Kuipers (1988) proposed a qualitative reasoning with incomplete quantitative measures. His basic idea is the following.
Assume that a system has several parameters and the relations among parameters are represented by algebra formulas, differential equations, or functions. Now, only partial knowledge of the parameters is known, for example, the variation range of the parameters, and the variation range can be represented by intervals. The problem is how to narrow the variation ranges via the known variation ranges of parameters and relations among them. Kuipers called it the propagation of incomplete quantitative knowledge and divides it into four categories.
(1) Propagation via arithmetic constraints 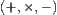 ,
,
(2) Propagation via monotonic function constraints,
(3) Propagation via number spaces,
(4) Propagation via temporal points 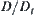 , where
, where 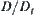 indicates the differential operation on t.
indicates the differential operation on t.
For example, 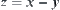 is known. And the variation ranges of x and y are known to be
is known. And the variation ranges of x and y are known to be 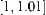 and
and 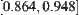 , respectively. It’s easy to find the variation range of z via the arithmetic constraint
, respectively. It’s easy to find the variation range of z via the arithmetic constraint 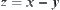 . It’s
. It’s 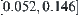 .
.
Again, constraint 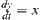 is known. The variation range of x in temporal interval
is known. The variation range of x in temporal interval 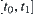 is
is 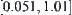 . Assume that
. Assume that 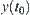 at
at 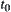 (
(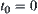 ). Now find the variation range of
). Now find the variation range of 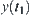 . From the mean value theorem, there exists
. From the mean value theorem, there exists 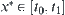 such that
such that 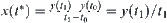 . If the variation range of
. If the variation range of 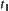 is
is 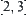 , then the variation range of
, then the variation range of 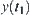 is
is 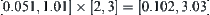 .
.
We next use the quotient space model to explain the above examples.
First, assume that 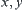 and
and  are three parameters and
are three parameters and 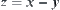 is a constraint.
is a constraint. 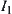 and
and 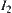 are variation ranges of x and y, respectively. Find the variation range of z.
are variation ranges of x and y, respectively. Find the variation range of z.
Let  and
and 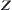 (real sets) be spaces that
(real sets) be spaces that 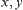 and
and  are located, respectively. Let
are located, respectively. Let 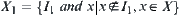 and
and 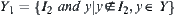 be quotient spaces of X and Y, respectively.
be quotient spaces of X and Y, respectively. 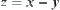 is regarded as a constraint on space
is regarded as a constraint on space  and Z, i.e.,
and Z, i.e., 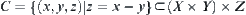 .
. 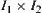 is an element of
is an element of 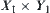 .
.
Second, find the section 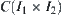 of C on
of C on 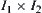 .
.
![]()
Therefore, the propagation of incomplete quantitative knowledge under different constraints is equivalent to finding the quotient constraint of a given quotient space.
4.6.3. The Procedure of Qualitative Reasoning
As viewed from different granularities, a qualitative reasoning is reasoning on some quotient space of the original space. The procedure of qualitative reasoning is summarized as follows.
(1) The variables, parameters and the constraints among these variables and parameters in the original problem space are analyzed and then simplified.
(2) All certain and uncertain information is represented in its proper quotient space.
(3) According to the analytical requirement, a proper qualitative space is constructed. The space is also a quotient space of the original one.
(4) All constraints and operators are projected on the qualitative space.
(5) The reasoning is made in that space.
The concepts of quotient operation, quotient constraint, the projection and synthetic method, and the approximation of upper space presented in the preceding sections can be used for making reasoning on quotient space.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
