The Expansion of Quotient Space Theory
Abstract
In this chapter, we extend the quotient space theory to general cases. It includes two aspects. First, the falsity- and truth-preserving principles are extended to a general quotient space approximation principle. Second, the quotient space theory based on equivalence relations is extended to that based on tolerant relations and closure operations.
When transforming a solution in the original space to a solution in its quotient space, or vice versa, a precise quotient space should be constructed. This is a problem-dependent work. Therefore, we present a general principle, the quotient space approximation principle. By the principle, a set of quotient spaces is constructed to approximate the original space. Then, the solution (or performance) of the original space is estimated from the solutions (or performances) of the quotient spaces. This is just the well-known multi-resolution system analysis and the multi-granular computing.
Since the quotient space approximation is a multi-resolution analysis method, it is closely related to wavelet analysis. Its connection to the second-generation wavelet analysis is discussed. Meanwhile, the concepts of quotient space and fractal geometry have a close relation. We also discuss the relation using the quotient space approximation principle.
Our original quotient space theory is based on equivalence relations, i.e., the boundaries of domain objects are clear-cut. In the chapter, it is extended to structures induced from closure operations and the tolerance relations. We also show that many useful properties in the original theory are still available under the expansion.
Keywords
closure operation; fractal geometry; quotient space approximation; wavelet analysis; tolerant relationChapter Outline
7.1 Quotient Space Theory in System Analysis
7.1.2 Quotient Space Approximation Models
7.2 Quotient Space Approximation and Second-Generation Wavelets
7.2.1 Second-Generation Wavelets Analysis
7.2.2 Quotient Space Approximation
7.2.3 The Relation between Quotient Space Approximation and Wavelet Analysis
7.3 Fractal Geometry and Quotient Space Analysis
7.3.2 Iterated Function Systems
7.4 The Expansion of Quotient Space Theory
7.4.2 Closure Operation-Based Quotient Space Theory
7.4.3 Non-Partition Model-Based Quotient Space Theory
7.4.4 Granular Computing and Quotient Space Theory
7.4.5 Protein Structure Prediction – An Application of Tolerance Relations
7.1. Quotient Space Theory in System Analysis
7.1.1. Problems
is a system, where f is its performance (attribute functions). We have a set 
of quotient spaces, where 
is the quotient performance of 
. Then, the following quotient space approximation problem emerged. That is, when space approaches to X, whether its performance approaches f. If the answer is yes, the f is called quotient space approachable. In this section, we will use the quotient space approximation model to analyze systems’ performances. We will discuss the necessary and sufficient conditions for quotient space approachable function f, and quotient space approximation methods.
, where 
is the convex closure of point set 
, a is an element on [X], or an equivalence class on X.7.1.2. Quotient Space Approximation Models
1. The Performance Description
2. The Convergence of a Set of Quotient Spaces
is a metric one, and d is its distance function.Definition 7.1
, letting 
, 
is called the diameter of 
.Definition 7.2
is an equivalence relation on 
, and [X] is its corresponding quotient space. Let 
. 
is called the fineness of .Definition 7.3
is a set of equivalence relations on X. If 
, then a set of the corresponding quotient spaces converges to X with respect to their grain-size, where 
is the corresponding quotient space of 
.3. Performance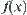 
of system X
Definition 7.4
on is defined as 
. The corresponding function [f] on [X] is defined according to a specified convex closure principle, where [X] is a quotient space of X. [f](a) is the quotient function induced from . 
and 
both are metric spaces. 
and 
are metric functions.Definition 7.5
on X such that 
,
.Definition 7.6
be a metric space composed by all bounded functions on X. Its distance is defined as 
.Definition 7.7
is a series of quotient spaces on X. 
is its corresponding quotient performance functions. When the series of quotient spaces converges to X in accordance with their grain-size, if 
(or simply ) on converges to f, then f is called quotient space absolutely approachable.Proposition 7.1
on metric space is quotient space absolutely approachable; the necessary and sufficient condition is that function on X is uniformly continuous.Proof
, when 
, have 
. Since converges to X, there exists 
such that when 
have 
. When 
,
. Thus
satisfies 
.
, i.e., 
on converges to f.
converges to 
. By reduction to absurdity, assuming that on is not uniformly continuous, there exists 
such that for any 
,
of quotient spaces such that their fineness satisfies 
, meanwhile 
and 
belong to the same class 
on . Let 
. Then, for 
, we have 
. When 
,
. This contradicts with the definition that f is an absolutely approachable function.Example 7.1
is a continuous function on X, 
. [0,1] is divided into i intervals equally. Letting each interval as an equivalence class, we have a quotient space . According to the inclusion principle of gaining quotient functions, we construct a quotient function . Since [0,1] is a bounded close set, is uniformly continuous on [0,1]. From Proposition 7.1, converges to f in accordance with their grain-size.Definition 7.8
of finite quotient spaces such that when the series converges to X, then 
on converges to , where is the corresponding quotient performance functions. f is called quotient space approachable, and 
is called one of its approximate quotient space series, where ‘a finite quotient space’ means that the number of elements in the space is finite.Proposition 7.2
is a metric space. :
is a performance function (measurable function), the necessary and sufficient condition that f is quotient space approachable is that f on X is bounded.Proof
, based on the inclusion principle, define a quotient function 
. Obviously, converges to f. is unbounded, for a finite quotient space [X], there at least exists an element a on [X] such that is unbounded at a. Namely, 
, 
does not always hold.Definition 7.9
Definition 7.10
, where 
indicates that 
and 
are tolerant. Let 
. 
is a quasi-quotient space on .Proposition 7.3
:
is a uniformly continuous function. If a series 
of quasi-quotient spaces converges to X with respect to their grain-size, a series of the corresponding quotient functions converges to f with respect to the grain-size as well.