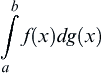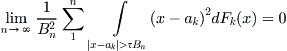Addenda B
Some Concepts and Properties of Integral and Statistical Inference
B.1. Some Properties of Integral
B.1.1. Functions of Bounded Variation
Definition B.1.1
![]()
The supremum of V is called total variation of 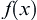 on
on  denoted by
denoted by  .
.
When 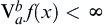 ,
, 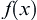 is called a function of bounded variation on
is called a function of bounded variation on  , or
, or 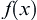 has a bounded variation on
has a bounded variation on  .
.
Proposition B.1.1
A monotonic function is a function of bounded variation.
Proposition B.1.2
A function of bounded variation is bounded.
Proposition B.1.3
The sum, difference and product of two functions of bounded variation are still functions of bounded variation.
Proposition B.1.4
If both 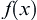 and
and  have a bounded variation and
have a bounded variation and 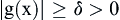 , then
, then 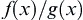 is still a function of bounded variation.
is still a function of bounded variation.
Proposition B.1.6
The necessary and sufficient condition that function 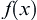 has a bounded variation is that
has a bounded variation is that 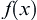 can be represented by the difference of two increasing functions.
can be represented by the difference of two increasing functions.
Proposition B.1.7
If 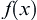 has a bounded variation on
has a bounded variation on  , then
, then 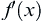 is finite almost everywhere on
is finite almost everywhere on  , and is integrable on
, and is integrable on  , where
, where 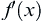 is the differential of
is the differential of 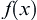 .
.
Proposition B.1.8
Any function of bounded variation can be represented by the sum of its jump function and a continuous function of bounded variation.
Proposition B.1.9 (Herlly’ Principle of Selection)
Define an infinite number 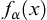 of functions of bounded variation on
of functions of bounded variation on  , and denoted by
, and denoted by 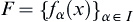 . If there is a constant
. If there is a constant 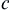 such that
such that  and
and 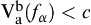 , then a sequence
, then a sequence 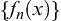 of everywhere convergent functions on
of everywhere convergent functions on  can be selected from F and its limit function
can be selected from F and its limit function 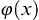 still has a bounded variation.
still has a bounded variation.
B.1.2. LS Integral
Definition B.2.1
![]()
When  , if the sum converges to the same limit
, if the sum converges to the same limit  independent of the selection of
independent of the selection of 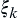 , then limit
, then limit 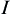 is called
is called 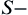 integral of
integral of 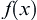 with respect to
with respect to  denoted by
denoted by

Proposition B.2.2
If 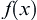 is continuous on
is continuous on  ,
,  has differential
has differential 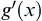 everywhere and
everywhere and 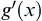 is
is  integrable (Riemann integrable), then
integrable (Riemann integrable), then
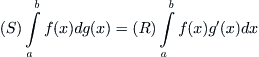
Proposition B.2.3
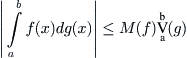
Proposition B.2.4
If  is a function of bounded variation on
is a function of bounded variation on  ,
,  is a sequence of continuous functions on
is a sequence of continuous functions on  and uniformly converges to a continuous function
and uniformly converges to a continuous function 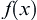 , then
, then 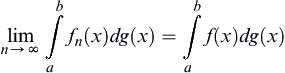 .
.
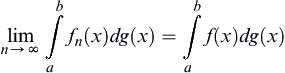 .
.Proposition B.2.5
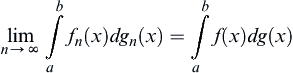 .
.Definition B.2.2
If 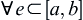 ,
, 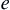 is measurable set and has its corresponding value
is measurable set and has its corresponding value 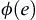 , then
, then 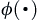 is called a set function on
is called a set function on  . Given
. Given 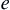 , when
, when 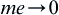 have
have 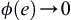 , then
, then 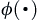 is called an absolutely continuous function, where
is called an absolutely continuous function, where 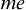 is the measure of
is the measure of 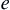 .
.
For countable mutually disjoint measurable sets 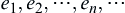 , have
, have 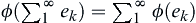 , then
, then 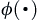 is called a completely additive set function.
is called a completely additive set function.
Definition B.2.3
![]()
Define 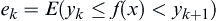 on
on  and construct a sum as
and construct a sum as
![]()
If  and
and  have the same limit
have the same limit  independent of the selection of
independent of the selection of  , then
, then 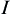 is called
is called 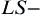 integral (Lebesgue-Stieltjes integral) of
integral (Lebesgue-Stieltjes integral) of 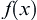 with respect to
with respect to 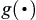 .
.
B.1.3. Limit Under Integral Symbol
Proposition B.3.1
![]()
Definition B.3.1
Assume that  is a family of integrable functions on
is a family of integrable functions on 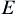 . If for
. If for 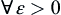 , there exists
, there exists 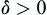 , when
, when  and
and  , for all
, for all 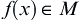 ,
, 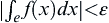 uniformly holds,
uniformly holds, 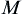 is called absolutely equicontinous integral on
is called absolutely equicontinous integral on 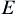 .
.
Proposition B.3.2 (Vitali Theorem)
A sequence 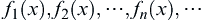 of functions converges in measure to
of functions converges in measure to 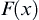 on
on 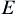 ,
,  is integrable on
is integrable on 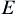 and
and 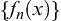 has absolutely equicontinuous integral on
has absolutely equicontinuous integral on 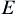 , then
, then 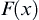 is integrable on
is integrable on 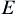 and
and
![]()
Proposition B.3.3
Corollary B.3.1
Assume that 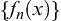 is a sequence of integrable functions and
is a sequence of integrable functions and 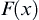 is an integrable function on a measurable set
is an integrable function on a measurable set 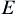 . For any measurable set
. For any measurable set  , if
, if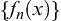 has absolutely equicontinuous integral on
has absolutely equicontinuous integral on 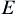 .
.
![]()
Proposition B.3.4
![]()
The necessary and sufficient condition of the above result is that 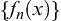 has absolutely equicontinuous integral on
has absolutely equicontinuous integral on 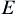 .
.
Proposition B.3.5 (Vallee-Poussin Theorem)
Proposition B.3.6
If  , is a family of functions on
, is a family of functions on 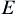 having absolutely equicontinuous integral, then there exists a monotonically increasing function
having absolutely equicontinuous integral, then there exists a monotonically increasing function 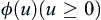 such that
such that 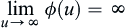 and
and 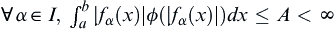 , where
, where 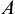 is a constant independent of
is a constant independent of 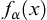 .
.
Proposition B.3.7
B.2. Central Limit Theorem
![]()
Proposition B.2.1
Corollary B.2.1
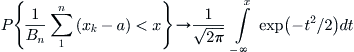
Proposition B.2.2
![]()
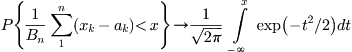
Definition B.2.1
Proposition B.2.3
Proposition B.2.4
B.3. Statistical Inference
B.3.1. SPRT Method
Definition 3.1.1
A hypothesis testing problem: the simple null hypothesis 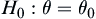 and the simple alternative hypothesis
and the simple alternative hypothesis 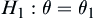 . Let
. Let
![]()
![]()
The testing procedure is the following
Given constants 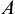 and
and 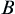 . Assume that
. Assume that 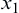 is the first observation of the subsample. Calculate
is the first observation of the subsample. Calculate 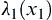 .
.
If 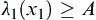 , then stop the observation and reject the null hypothesis
, then stop the observation and reject the null hypothesis 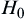 .
.
If 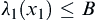 , then stop the observation and accept the null hypothesis
, then stop the observation and accept the null hypothesis 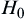 .
.
If 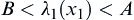 , then continue to get the second observation
, then continue to get the second observation 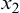 .
.
Generally, if from the 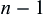 -th observation the ‘stopping decision’ cannot be made, then continue to get the n-th observation
-th observation the ‘stopping decision’ cannot be made, then continue to get the n-th observation 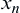 and calculate
and calculate  .
.
If 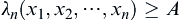 , then stop sampling and reject
, then stop sampling and reject 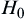 .
.
If 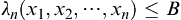 , then stop sampling and accept
, then stop sampling and accept 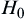 .
.
If 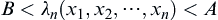 , then continue sampling.
, then continue sampling.
The above testing procedure is called Sequential Probability Ratio Test denoted by SPRT. Constants 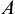 and
and 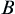 are called the stopping boundaries of SPRT.
are called the stopping boundaries of SPRT.
Proposition 3.1.1
If 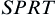 stops with probability 1, its stopping boundaries are constants
stops with probability 1, its stopping boundaries are constants 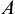 and
and 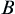 , and significance level is
, and significance level is 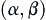 , then
, then
![]()
Proposition 3.1.2
If 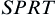 stops with probability 1, stopping boundary
stops with probability 1, stopping boundary  and significance level
and significance level 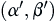 , then
, then 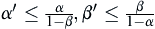 .
.
Let
![]()
![]()
![]()
The stopping rule of 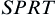 is the following.
is the following.
If 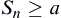 , then reject
, then reject 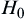 .
.
If 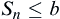 , then accept
, then accept 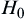 .
.
If  , then continue sampling.
, then continue sampling.
Proposition 3.1.3
If for a given parameter 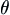 , have
, have 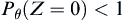 , where
, where 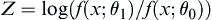 , then there exist
, then there exist 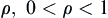 ,
,  and
and 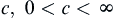 such that
such that .
.
![]()
Proposition 3.1.4
Assume that 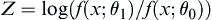 . If for
. If for 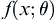 , have
, have 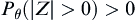 , then
, then 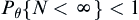 .
.
Proposition 3.1.5
![]()
Especially, if 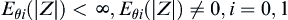 , then
, then
![]()
![]()
Proposition 3.1.6
Assume that 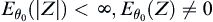 . For a
. For a 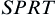 with stopping probability one and significance level
with stopping probability one and significance level 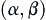 , the following formula holds
, the following formula holds
![]()
![]()
Proposition 3.1.7
For simple null hypothesis 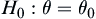 and simple alternative hypothesis
and simple alternative hypothesis 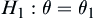 testing, among the testing methods, including sequential and non-sequential, that have
testing, among the testing methods, including sequential and non-sequential, that have 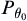 (reject
(reject 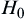 )
) ,
, 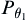 (accept
(accept 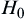 )
)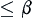 and
and  , the
, the 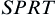 with significance level
with significance level 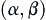 has the minimums of
has the minimums of 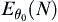 and
and 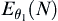 .
.
B.3.2. ASM Method
3.2.1. Normal Distribution
![]()
![]() (II.1)
(II.1)
![]()
When  is unknown, define a sampling process and assume that
is unknown, define a sampling process and assume that 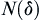 is its stopping variable (when sampling stops Formula (II.1) holds). If
is its stopping variable (when sampling stops Formula (II.1) holds). If 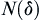 satisfies the following formula
satisfies the following formula
![]()
Then the process is called asymptotically efficient. The corresponding method is called asymptotically efficient testing method with fixed width of the mean confident interval, denoted by ASM. The distribution of xi is assumed to be  .
.
Definition 3.2.1
Let n1, n2 . For each
. For each  , calculate
, calculate 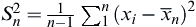 . Define stopping variable
. Define stopping variable 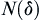 as the minimal integer satisfying the following formula
as the minimal integer satisfying the following formula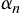 is a series of positive constants and converges to
is a series of positive constants and converges to 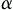 ,
, 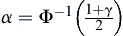 .
.
![]() (II.2)
(II.2)
Proposition 3.2.1
Assume that 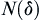 is a stopping variable defined by Formula (II.2). Then, we have the following properties.
is a stopping variable defined by Formula (II.2). Then, we have the following properties.
(1) 
(2) If 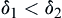 , then
, then 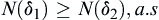 and
and 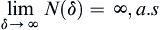
where, symbol a.s means almost everywhere.
(3) 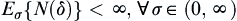 ,
,  holds
holds
(4) 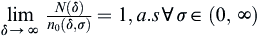
(5) 
(6) 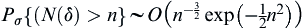
Proposition 3.2.2
Proposition 3.2.3
B.3.2. General Cases
Definition 3.2.2
Define 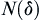 as the minimal integer satisfying the following formula
as the minimal integer satisfying the following formula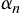 a series of positive constants and converges to
a series of positive constants and converges to 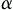 ,
,  .
.
![]() (II.3)
(II.3)
Proposition 3.2.4
Assume that  is a series of positive random variables
is a series of positive random variables 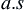 and
and 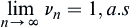 . Let
. Let  be a series of constants satisfying the following condition
be a series of constants satisfying the following condition
![]()
For 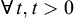 , define
, define 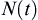 as the minimal integer satisfying the following formula
as the minimal integer satisfying the following formula
![]()
Then, 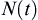 is a non-decreasing stopping variable of t and
is a non-decreasing stopping variable of t and
(1) 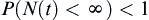
(2) 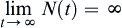
(3) 
(4) 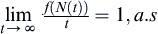 .
.
If 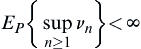 again, then
again, then 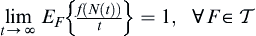 .
.
Proposition 3.2.5 (Chow-Robbins Theorem)
Assume that 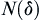 is a stopping variable defined by Formula (II.3). Then,
is a stopping variable defined by Formula (II.3). Then,
Proposition 3.2.6
![]()
Then, we have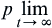 is a convergent in measure limit and
is a convergent in measure limit and 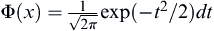 .
.
![]()
The above proposition is the extension of common central limit theorem. In the common theorem N is a constant variable but 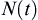 is a random variable.
is a random variable.
Proposition 3.2.7
Let 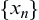 be a sequence of random variables satisfying the following properties
be a sequence of random variables satisfying the following properties
(1) There exist real number 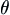 , distribution function
, distribution function 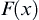 and a series
and a series 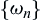 of real such that for all continuous points of F the following formula holds
of real such that for all continuous points of F the following formula holds
![]()
(2) 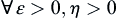 , there exists a sufficiently large
, there exists a sufficiently large 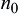 and sufficient small positive number c such that when
and sufficient small positive number c such that when  have
have
![]()
Let 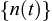 be a sequence of ascending integers and
be a sequence of ascending integers and 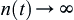 . Let
. Let 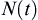 be a stopping variable,
be a stopping variable, 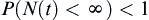 and
and  . Then, for all continuous points of
. Then, for all continuous points of 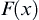 , we have
, we have
![]()
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.