7.4. The Expansion of Quotient Space Theory
7.4.1. Introduction
The quotient space theory we have discussed so far is based on the following two main assumptions. (1) The domain structure is limited to topology. (2) The domain granulation is based on equivalence relations, i.e., classification without overlap. Now, we will relax the two restrictions. First, we consider the structures formed by closure operations that are broader than topological ones. Second, domain granulation will be extended from equivalence relations to tolerance relations.
7.4.2. Closure Operation-Based Quotient Space Theory
There is a variety of closure operations, so different structures can be defined by the operations. The domain structures described by closure operations are broader than topological ones generally. For example, the pre-topology defined by closure operations under the Cech’s sense is more universal than well-known topology defined by open sets (Cech, 1966). But the topology defined by Kuratowski closure operation is equivalent to well-known topology.
Now, we introduce some basic concepts about closure space (see Addenda A for more details).
Definition 7.27
Assume that X is a domain. If mapping 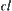 :
: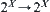 satisfies the following axioms, where
satisfies the following axioms, where 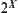 is a power set of X,
is a power set of X,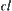 is called a closure operation on
is called a closure operation on  , correspondingly
, correspondingly 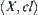 is called a closure space,
is called a closure space,  is a
is a 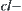 closure of
closure of  , and for simplicity,
, and for simplicity,  is indicated by
is indicated by 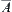 .
.
![]()
![]()
![]()
Proposition 7.6
Assume that 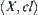 is a closure space, then
is a closure space, then
(1) 
(2) 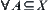 ,
,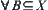 , if
, if 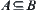 , then
, then 
(3) For any family 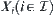 of subsets on
of subsets on  ,
, 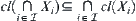 .
.
Definition 7.28
![]()
If 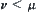 , then
, then  is called coarser than
is called coarser than  , or
, or  is finer than
is finer than  .
.
Proposition 7.7
Binary relation 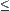 is a semi-order relation on
is a semi-order relation on 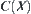 .
. 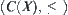 has the greatest element
has the greatest element 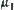 and the least element
and the least element 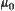 . For
. For 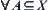 , if
, if 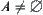 then
then 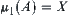 , otherwise
, otherwise 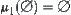 . And for
. And for  ,
, 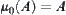 . Furthermore, any subset
. Furthermore, any subset 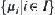 on
on 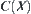 and
and 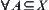 ,
, 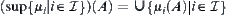 holds, i.e.,
holds, i.e., 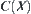 is order complete with respect to ‘
is order complete with respect to ‘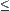 ’.
’.
7.4.2.1. The Construction of Quotient Closure and its Property
![]()
Especially, when 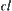 is a topological closure operation, the structure decided by
is a topological closure operation, the structure decided by 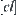 is a corresponding quotient topology on
is a corresponding quotient topology on  .
.
Assume that 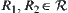 and
and  ,
,  is a nature projection, and
is a nature projection, and 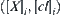 ,
,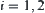 , is a quotient space having a closure structure, or simply a quotient closure structure. Since
, is a quotient space having a closure structure, or simply a quotient closure structure. Since  ,
,  is a nature projection from
is a nature projection from 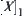 to its quotient set
to its quotient set 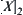 .
.  on
on 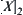 is a closure operation induced from projection
is a closure operation induced from projection 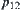 with respect to closure operation
with respect to closure operation 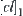 . Thus,
. Thus, 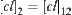 (Cech, 1966). Generally, the similar result can be obtained for a chain of equivalence relations. Then we have the following proposition.
(Cech, 1966). Generally, the similar result can be obtained for a chain of equivalence relations. Then we have the following proposition.
Proposition 7.8
Assume that 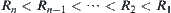 is a chain of equivalence relations on
is a chain of equivalence relations on 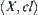 .
. is a nature projection.
is a nature projection. 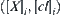 ,
,  , is a corresponding quotient closure space.
, is a corresponding quotient closure space. 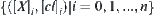 composes a hierarchical structure, where
composes a hierarchical structure, where 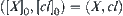 .
.
The similar falsity-preserving principle in closure spaces is the following (Chen, 2005).
Proposition 7.9
If 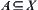 is a connected subset on
is a connected subset on 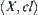 , the image
, the image 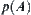 of
of 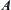 under the projection p is a connected subset on
under the projection p is a connected subset on 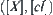 .
.
Theorem 7.6 (Falsity-Preserving Principle)
From Chapter 1, it’s known that a semi-order relation under the quotient mapping only maintains the reflexivity and transitivity but does not necessarily maintain anti-symmetry generally. For the closure spaces, we will prove that the quasi-semi-order structures are invariant under the quotient mapping (projection), with the help of the continuity of the mapping, but the semi-order structure cannot maintain unchanged under the mapping generally.
Proposition 7.10
Assume that 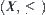 is a quasi-semi-order space.
is a quasi-semi-order space. 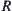 is an equivalence relation on X, and
is an equivalence relation on X, and  is the corresponding quotient set. Then, there exists a quasi-semi-order
is the corresponding quotient set. Then, there exists a quasi-semi-order 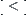 on
on  such that the nature projection is order-preserving, i.e.,
such that the nature projection is order-preserving, i.e.,  , we have
, we have
![]()
Proof
Since 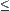 is a quasi-semi order on X, define an operation induced from
is a quasi-semi order on X, define an operation induced from 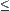 as follows
as follows
![]()
It’s easy to prove that 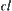 is a closure operation on X. In fact,
is a closure operation on X. In fact, 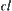 is a topologic closure operation with the Alexandroff property. If from closure space
is a topologic closure operation with the Alexandroff property. If from closure space 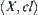 define a quasi-semi-order
define a quasi-semi-order 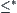 as
as 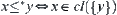 , then
, then 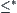 is the same as
is the same as 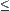 . This means that closure operation
. This means that closure operation 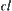 and quasi-semi order
and quasi-semi order 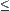 are interdependent.
are interdependent.
If 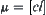 is a quotient closure operation on
is a quotient closure operation on  with respect to
with respect to 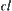 , then
, then 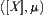 is a topologic closure space. Define a quasi-semi-order
is a topologic closure space. Define a quasi-semi-order 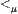 on
on  as
as
![]()
Finally, we show that 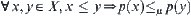 . In fact, we have
. In fact, we have
![]()
![]()
![]()
In summary, there exists a quasi-semi-order relation on the quotient structure of a quasi-semi-order space such that the corresponding nature projection is order-preserving.
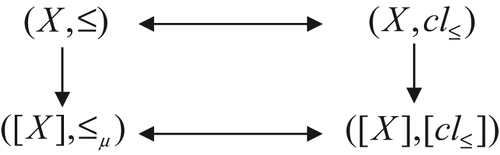
The order-preserving processing processes of quotient closure spaces are shown in Fig. 7.3, where 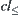 indicates the closure topology induced from ≤,
indicates the closure topology induced from ≤, 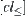 is its corresponding quotient topology,
is its corresponding quotient topology, 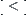 is a quasi-semi-order on [X] induced from
is a quasi-semi-order on [X] induced from 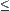 ,
,  is a quasi-semi-order induced from topology
is a quasi-semi-order induced from topology  , and [cl] on [X] is a topology induced from cl.
, and [cl] on [X] is a topology induced from cl.
The whole quasi-semi-order relations satisfying reflexivity and transitivity on a domain and the whole Alexandroff topologies on the domain are one–one correspondence. Especially, the whole semi-order relations, i.e., the quasi-semi-order satisfying anti-symmetry as well, and whole Alexandroff topologies satisfying 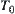 -separation axiom are one–one correspondence. So the order structure may be regarded as a specific topological structure, and a specific closure structure spontaneously.
-separation axiom are one–one correspondence. So the order structure may be regarded as a specific topological structure, and a specific closure structure spontaneously.
Since 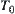 -separation axiom does not satisfy divisibility, the order relation
-separation axiom does not satisfy divisibility, the order relation 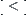 on quotient space
on quotient space  of semi-order space
of semi-order space 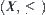 that is constructed by the above method does not have anti-symmetry generally, although its nature projection is an order-preserving mapping. As in Chapter 1, by merging and decomposing, the original equivalence relation R can be changed to R∗ such that corresponding relation
that is constructed by the above method does not have anti-symmetry generally, although its nature projection is an order-preserving mapping. As in Chapter 1, by merging and decomposing, the original equivalence relation R can be changed to R∗ such that corresponding relation 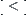 satisfies the anti-symmetry in space
satisfies the anti-symmetry in space 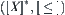 .
.
7.4.2.2. The Synthesis of Different Grained Worlds
So far we have shown that a new space can be constructed from given spaces through synthesis methods, when their structure is topologic. We also show that the synthetic space is the least upper bound one, and the projection from the synthetic space on the given spaces plays an important role. In fact, the synthetic principle can be represented as an optimization problem with respect to 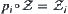 , where
, where 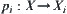 is a projection from the original to quotient spaces,
is a projection from the original to quotient spaces, 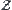 and
and 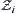 represent the domain, topological structure, or attribute function of the original and quotient spaces, respectively. The synthetic space is either the least upper bound, or the greatest lower bound space among the given spaces. In this section, we will consider the synthetic problem under the closure structures.
represent the domain, topological structure, or attribute function of the original and quotient spaces, respectively. The synthetic space is either the least upper bound, or the greatest lower bound space among the given spaces. In this section, we will consider the synthetic problem under the closure structures.
Define  .
. 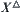 is a quotient set corresponding to
is a quotient set corresponding to 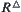 , and the least upper bound of
, and the least upper bound of 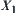 and
and 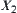 in partition lattice
in partition lattice  . Both
. Both 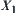 and
and 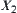 are quotient sets of
are quotient sets of 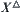 .
. 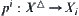
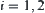 are their corresponding projections. It’s easy to show that for each
are their corresponding projections. It’s easy to show that for each 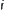 , there exists
, there exists 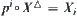 such that
such that 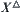 is projected onto
is projected onto  by projection
by projection 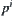 , and quotient space
, and quotient space 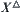 satisfies the synthetic principle, i.e.,
satisfies the synthetic principle, i.e., 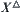 is the coarsest partition among all partitions that satisfy
is the coarsest partition among all partitions that satisfy 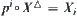 . Dually, define
. Dually, define 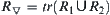 , where
, where 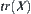 denotes the set obtained after implementing transitive operation on elements of X. Quotient space
denotes the set obtained after implementing transitive operation on elements of X. Quotient space 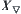 corresponding to
corresponding to 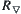 is the greatest lower bound of
is the greatest lower bound of 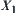 and
and 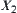 in partition lattice
in partition lattice 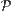 . For
. For 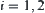 ,
, 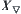 is the quotient set of
is the quotient set of  , and its corresponding projection is
, and its corresponding projection is  . It’s easy to show that
. It’s easy to show that 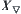 satisfies the synthetic principle, i.e.,
satisfies the synthetic principle, i.e., 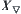 is the finest partition among all partitions that satisfy
is the finest partition among all partitions that satisfy 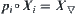 .
.
According to the synthetic principle,  should be defined as the solution of a set
should be defined as the solution of a set  ,
,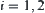 , of equations. If their solution is not unique, some optimization criteria should be added in order to have an optimal one. Dually,
, of equations. If their solution is not unique, some optimization criteria should be added in order to have an optimal one. Dually, 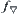 should be defined as the solution of a set
should be defined as the solution of a set 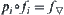 ,
,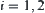 , of equations which similar to solving
, of equations which similar to solving  .
.
A new closure operation can be constructed in the following way, i.e., a new closure operation (or a set of closure operations) can be generated projectively, or inductively by a known mapping (or a set of mappings), respectively. The following proposition shows the relation between the two generation methods.
Proposition 7.11 (Cech, 1966)
First, we consider the construction of closure operation 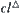 .
. 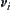 is a closure operation on
is a closure operation on  that generated projectively by
that generated projectively by 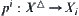 with respect to closure operation
with respect to closure operation 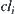 . Since
. Since 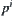 is a surjection,
is a surjection, 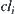 is generated inductively by
is generated inductively by 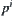 with respect to closure operation
with respect to closure operation 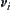 . Space
. Space 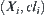 is a quotient closure space of
is a quotient closure space of 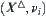 with respect to equivalence relation
with respect to equivalence relation 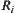 . Defining closure operation
. Defining closure operation 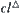 as
as  , then
, then 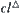 on
on 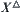 is the coarsest one among all closure operations that make each
is the coarsest one among all closure operations that make each  continuous. Closure space
continuous. Closure space  is the least upper bound of synthetic spaces
is the least upper bound of synthetic spaces 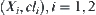 , but an explicit expression of
, but an explicit expression of 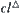 cannot be obtained generally.
cannot be obtained generally.
Dually, the construction of closure operation 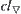 is as follows.
is as follows. 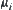 is a closure operation on
is a closure operation on 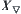 that generated inductively by
that generated inductively by  with respect to closure operation
with respect to closure operation 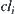 , i.e.,
, i.e., 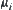 is the finest one on
is the finest one on 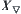 among all closure operations that make each
among all closure operations that make each 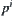
 continuous. Defining closure operation
continuous. Defining closure operation 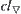 as
as 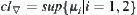 , then
, then 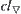 is the finest one on
is the finest one on 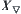 among all closure operations that make each
among all closure operations that make each  continuous. Closure space
continuous. Closure space 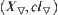 is the greatest lower one of synthetic spaces
is the greatest lower one of synthetic spaces 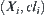
 . The expression of
. The expression of 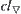 is the following.
is the following.
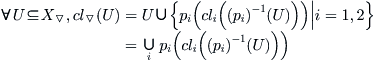
The synthetic process of quotient closure spaces can intuitively be shown in Fig. 7.4.
7.4.3. Non-Partition Model-Based Quotient Space Theory
The quotient space theory that we have discussed so far is based on a partition model, i.e., a complete lattice composed by all equivalence relations on a domain, or a partition lattice. The quotient space theory based on the partition model that we called traditional theory is too rigorous. Many real problems do not necessarily meet the requirement, for example, classification with overlap, or with incomplete knowledge, etc. If abandoning the transitivity condition in an equivalence relation, then we have a tolerance relation. Tolerance relation is a broader binary relation than the equivalence one, but still has good attributes. So the tolerance relation-based quotient space theory is a very useful extension of the traditional one.
7.4.3.1. Tolerance Relations
Definition 7.29
Definition 7.30
For 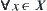 , define
, define 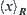 as a
as a 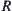 -relevant class of
-relevant class of  , i.e.,
, i.e.,  . The whole
. The whole 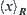 is denoted by
is denoted by  , where
, where 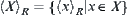 , for simplicity,
, for simplicity, 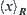 and
and  are denoted by
are denoted by 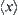 and
and 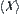 respectively, if it does not cause confusion.
respectively, if it does not cause confusion.
Proposition 7.12
If and only if tolerance relation 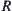 satisfies transitivity, then
satisfies transitivity, then  is a partition of X.
is a partition of X.
Theorem 7.7
Assume that 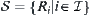 is the whole tolerance relations on X, and
is the whole tolerance relations on X, and 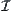 is a set of subscripts.
is a set of subscripts.
(1)  and
and  are tolerance relations on X.
are tolerance relations on X.
(2) Define a binary relation 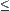 on
on 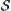 as
as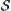 composes a complete lattice with respect to relation
composes a complete lattice with respect to relation 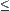 , denoted by
, denoted by 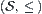 . The intersection operation
. The intersection operation 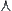 and union operation
and union operation 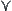 on lattice
on lattice 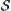 are defined as follows.
are defined as follows. and
and 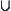 are set intersection and union operations, respectively.
are set intersection and union operations, respectively.
![]()
![]()
(3) 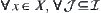 ,
, 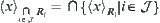 ,
, 
The proof of the theorem is obvious.
A complete lattice 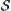 , composed by all tolerance relations on a domain, is similar to a complete lattice
, composed by all tolerance relations on a domain, is similar to a complete lattice 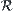 , composed by all equivalence relations on the domain or a partition lattice
, composed by all equivalence relations on the domain or a partition lattice 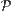 . Both can be used to describe multi-granular worlds but they are different. In partition, the classes are mutually disjointed. In classification based on tolerance relations the classes do not necessarily mutually disjoint.
. Both can be used to describe multi-granular worlds but they are different. In partition, the classes are mutually disjointed. In classification based on tolerance relations the classes do not necessarily mutually disjoint.
7.4.3.2. Tolerance Relation-Based Quotient Space Theory
Definition 7.31
t is a mapping from set  to set
to set 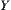 . An equivalence relation
. An equivalence relation 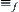 on
on  can be induced from t as follows
can be induced from t as follows
![]()
For simplicity, 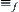 is denoted by
is denoted by  .
. 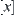 ,
, 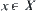 , is an equivalence class with respect to equivalence relation
, is an equivalence class with respect to equivalence relation  .
.  is the corresponding quotient set, and
is the corresponding quotient set, and 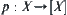 is a nature projection.
is a nature projection.
Definition 3.30
(1) t is a surjection
(2) for 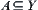 ,
, 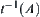 is an open set on
is an open set on 
then, Proposition 7.13
t is a quotient mapping from topologic space 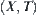 to topologic space
to topologic space 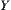 .
.  is an equivalence relation on
is an equivalence relation on  induced from t.
induced from t.  is a quotient topologic space with respect to nature projection
is a quotient topologic space with respect to nature projection 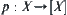 . Then, topologic spaces
. Then, topologic spaces  and
and 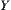 are homeomorphism, where homeomorphous mapping
are homeomorphism, where homeomorphous mapping 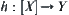 satisfies
satisfies 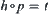 , equivalently,
, equivalently, 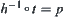 .
.
The proposition shows that when 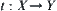 is a quotient mapping,
is a quotient mapping, 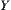 can be regarded as a quotient space of
can be regarded as a quotient space of  . t is just the corresponding pasting mapping. In fact, quotient spaces and quotient mappings are closely related concepts. The nature projection discussed in Chapter 1 is a specific quotient mapping that satisfies the conditions (1) and (2) in Definition 7.32.
. t is just the corresponding pasting mapping. In fact, quotient spaces and quotient mappings are closely related concepts. The nature projection discussed in Chapter 1 is a specific quotient mapping that satisfies the conditions (1) and (2) in Definition 7.32.
Definition 7.33
t is a surjection from 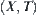 onto
onto 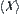 . For
. For 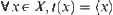 , define a topology on
, define a topology on 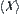 as
as 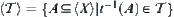 . That is,
. That is, 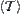 is the finest among topologies that make the surjection t from topologic space
is the finest among topologies that make the surjection t from topologic space 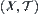 onto
onto  continuous.
continuous.
Proposition 7.14
t is a quotient mapping from space 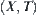 to
to 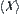 . Topologic spaces
. Topologic spaces  and
and 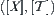 are homeomorphism, where
are homeomorphism, where 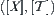 is a pasting space induced from t.
is a pasting space induced from t.
Although 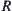 is not an equivalence relation, i.e.,
is not an equivalence relation, i.e., 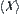 cannot compose a partition on X, since there is no distinction among homeomorphous spaces in some sense, from Proposition 3.17 it’s shown that the traditional quotient space theory is still available to the tolerance relation. But since the elements on
cannot compose a partition on X, since there is no distinction among homeomorphous spaces in some sense, from Proposition 3.17 it’s shown that the traditional quotient space theory is still available to the tolerance relation. But since the elements on 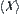 as subsets on X are no longer mutually disjointed, the computational complexity discussed in Chapter 2 will not hold, likely increases.
as subsets on X are no longer mutually disjointed, the computational complexity discussed in Chapter 2 will not hold, likely increases.
The construction of quotient attribute 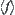 is the same as that of a traditional one. Therefore, if tolerance relation
is the same as that of a traditional one. Therefore, if tolerance relation 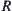 and space
and space 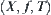 are given, the quotient space
are given, the quotient space 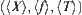 can be constructed.
can be constructed.
Similar to the traditional theory, we have the following property.
Proposition 7.15
If 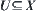 is a connected subset on X, then
is a connected subset on X, then 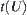 is a connected subset on
is a connected subset on 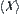 .
.
Now, we consider the order preserving property. Assume that 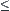 on
on  is a quasi-semi-order structure.
is a quasi-semi-order structure.  on
on 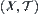 is an Alexzandroff topology determined by the quasi-semi-order
is an Alexzandroff topology determined by the quasi-semi-order 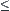 .
. 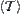 on
on  is a quotient topology with respect to quotient mapping
is a quotient topology with respect to quotient mapping 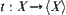 . Define a binary relation
. Define a binary relation 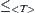 on
on 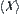 as follows
as follows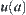 is an open neighborhood of
is an open neighborhood of  .
.
![]()
Relation 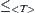 is just a specified quasi-semi-order determined by
is just a specified quasi-semi-order determined by 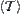 . Since
. Since  and
and 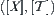 are homeomorphism, from Proposition 3.13, there exists a quasi-semi-order
are homeomorphism, from Proposition 3.13, there exists a quasi-semi-order 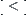 on
on  such that
such that  , if
, if 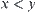 then
then 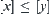 . The following proposition shows that quasi-semi-order relation
. The following proposition shows that quasi-semi-order relation 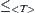 has the order preserving property.
has the order preserving property.
Proposition 7.16
If  and
and 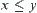 , then
, then 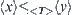 .
.
Proof
Since 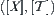 and
and  are homeomorphous, the quasi-semi-order
are homeomorphous, the quasi-semi-order 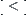 on [X] induced from
on [X] induced from 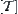 and the quasi-semi-order
and the quasi-semi-order 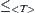 on
on 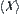 induced from
induced from 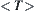 are equivalent.
are equivalent.
Again from the order preserving of 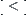 ,
, 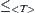 on
on 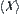 has order-preserving as well.
has order-preserving as well.
The order-preserving property in tolerance relation-based quotient spaces can be shown in Fig. 7.5 intuitively.
When we discuss the order-preserving property, the homeomorphism of topologic spaces  and
and 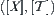 plays an important role. Similarly, the above homeomorphous relation can still play a significant role in the synthetic problem.
plays an important role. Similarly, the above homeomorphous relation can still play a significant role in the synthetic problem.
7.4.4. Granular Computing and Quotient Space Theory
Quotient space-based problem-solving theory is a multi-granular computing model under the framework of set theory. We have dealt with the following problems. First, the projection problem is that given a quotient set, to find the representations of attribute and structure on the set, i.e., the descriptions of the coarse-grained world and the relation to the original one. Second, the synthesis problem is that given different views of the world, to find a new understanding of the world based on the known knowledge. Third, the reasoning problem is the reasoning over different grain-size worlds. The final problem is how to choose a proper grain-size world in order to reduce the computational complexity of multi-granular computing.
Now, we discuss granulation and granular computing from the quotient space theory view point.
7.4.4.1. Granule, Granulation and Granular World
In quotient space theory, a ‘granule’ is defined as a subset in a space (domain). In the partition model, the subset is an equivalence class and an element in its quotient space, whose inner structure is determined by the corresponding partition. Each subset can be represented by a complete graph. For example, in a grained level {[1],[4]}={{1,2,3},{4,5}}, element [1] has three components (elements) {1,2,3} and can be represented by a complete graph. Similarly, element [4] has two components {4,5} and can be represented by a complete graph as well. Any two elements are mutually disjointed. In the tolerance relation model, the subset consists of all elements that have tolerance relations. They may have a center that can be represented by a stellate graph. They may have several centers that can also be represented by a stellate graph, when the centers are regarded as a whole. For example, in a grained level {<1>,<2>,<4>,<5>}={{1,2},{1,2,3,4},{2,3,4,5},{3,4,5}}, where ‘bold’ Arabic numerals indicate ‘centers’. Element <1> is a graph with component ‘1’ as a center. Element <4> is a graph with components {3,4} as centers, while components ‘2’ and ‘5’ do not have any connected edge.
In quotient space theory, the granulation criterion is equivalence or tolerance relation. The relation may be induced from attributes, or relevant to them. This is different from the rough set theory. When an equivalence or tolerance relation is given, we have a coarse-grained world. In the world, each element can be regarded as independent; while as subsets in the original domain, they may be mutually disjointed or have an overlapping portion. In addition, a coarse-grained world may have a structure, for example, topologic, closure or order structure. The structure is obtained by a quotient mapping from the original world. The continuity of the quotient mapping plays an important role that we have discussed in previous sections adequately.
7.4.4.2. The Multi-Granular Structure
When a granulation criterion is given, we have a grained world. When several granulation criteria are given, then we have a multi-grained world. What relation exists within the multi-granular world? In other words, what structure the multi-granular world has? In partition model, all equivalence relations compose a complete lattice. Correspondingly, all partitions compose a complete lattice as well. In the tolerance relation model, all tolerance relations compose a complete lattice. Specially, a chain of equivalence relations or tolerance relations is chosen, we have a hierarchical structure. In addition, the existence of complete lattice guarantees the closeness of the newly constructed grained worlds.
7.4.4.3. Granular Computing
In granular computing, the computational and inference object is ‘granules’. Quotient space theory deals with several basic problems of granular computing. For example, considering the computation of quotient attribute functions in a certain grained level, since the arguments of the functions are ‘granules’, their values may adopt the maximum, minimum, or mean of the attribute functions of all elements in the granule. If an algebraic operation is defined on a domain, it’s needed to consider the existence and uniqueness of its quotient operation on a certain grained level. We have discussed this problem in Chapter 4.
The descriptions of a problem in several grain-size worlds are given, how to choose a proper grain-size world to carry out the problem solving? Quotient space theory deals with the problem by information synthesis that mirrors the characteristics of human problem solving, i.e., viewing the same problem from different granularities, translating from one abstraction level to the others freely, and solving the problem at a proper grained level. Information synthesis includes domain, structure and attribute function. Here, the homomorphism principle plays an important role.
Falsity-preserving property is very important in the inference over a multi-granular world. With the help of the continuity of quotient mappings and the connectivity of sets, and considering the structure of domain, the computational complexity can be reduced by multi-granular computing based on quotient space theory.
7.4.5. Protein Structure Prediction – An Application of Tolerance Relations
In the section, we will use the binary relation satisfying anti-reflexivity and symmetry, i.e., equivalent to a tolerance relation, to define the sequence adjacency and topology adjacency in the amino acid sequence folding. Furthermore, we will explain the enhancement method for estimating the lower bound of energy of a protein obtained by the folding of its amino acid sequence, using the concept of tolerance relations.
7.4.5.1. Problem
Protein structure prediction is the prediction of the three-dimensional structure of a protein from its amino acid sequence that is a hot topic in bioinformatics (Martin, 2000). Generally, there are three methods to dealing with the problem, molecular dynamics, protein structure prediction and homology modeling. Different protein models may be established depending on the ways of describing the protein molecular and treating the interaction between amino acid residues and solution. The experimental result for small proteins implies that the primary state of proteins approaches the minimum of free energy. This widely accepted assumption becomes the foundation of protein structure prediction from a given amino acid sequence by means of computation.
Due to the complexity and large scale of protein structure, the simple models are adopted generally. A lattice model is one of the well-known models (Dill et al., 1995). In lattice models, each amino acid residue is represented as an equal size and is confined to regular lattices, the connection between them is assumed to be the same length. For simplicity, 2D rectangle or 3D cuboid lattice point representation of lattice models is adopted. We will only discuss the 2D lattice model below.
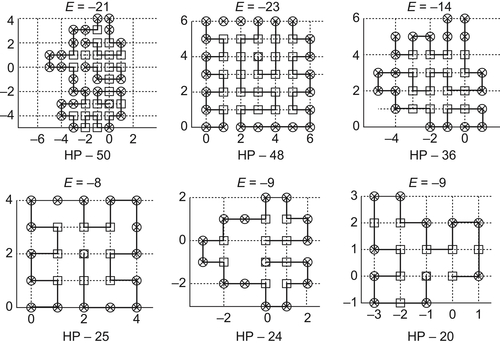
HP lattice model is a representative one (Lau and Dill, 1989, 1990). In the model, amino acids are divided into two categories: hydrophobic (H) and hydrophilic (P). The hydrophilic force is the important driving force behind the folding process. Under the impact of the force, after the folding of the amino acid sequence, the hydrophobic amino acids will concentrate in the center of the protein as far as possible in order for them to keep out of water. In Fig. 7.6(a) the inappropriate folding, (b) the appropriate folding of amino acid sequences are shown.
A sequence 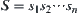 of amino acids is given, where
of amino acids is given, where 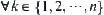 ,
, 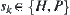 . After the folding of
. After the folding of 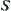 , we have protein
, we have protein 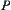 represented in a 2D-HP model as follows. Amino acids
represented in a 2D-HP model as follows. Amino acids 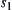 and
and 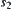 are confined in coordinates
are confined in coordinates 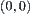 and
and 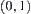 , respectively. For
, respectively. For  , the coordinate of
, the coordinate of 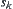 is represented by the directions of
is represented by the directions of 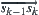 relative to
relative to 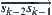 , i.e., forward, towards the left, and towards the right, respectively. Assume that the interaction of amino acids happens inside a topology adjacent pair, i.e., the amino acids in a pair are adjacent in their lattice but are not adjacent in their sequence. The interaction
, i.e., forward, towards the left, and towards the right, respectively. Assume that the interaction of amino acids happens inside a topology adjacent pair, i.e., the amino acids in a pair are adjacent in their lattice but are not adjacent in their sequence. The interaction 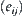 of amino acid pair
of amino acid pair  with type
with type 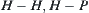 , or
, or 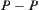 , is defined as follows respectively.
, is defined as follows respectively.
![]()
The energy of protein obtained by the folding of its amino acid sequence is defined as 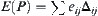 , where if and only if
, where if and only if 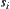 and
and 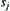 are topology adjacent,
are topology adjacent, 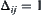 , otherwise
, otherwise 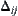 = 0.
= 0.
An amino acid sequence 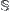 with length
with length  is given. Let
is given. Let 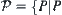 obtained by the folding of
obtained by the folding of 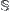 and the hydrophobic amino acids concentrate in the center of
and the hydrophobic amino acids concentrate in the center of 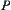 }. Under the widely accepted assumption, the protein-folding problem can be represented as follows.
}. Under the widely accepted assumption, the protein-folding problem can be represented as follows.
![]()
It has been shown in Nayak et al. (1999) that this is a NP-hard problem. There exists an (or several) optimal solution, or only several sub-optimal solutions.
7.4.5.2. The Estimation of the Lower Bound of Energy
Each anti-reflexive relation corresponds to a reflexive relation uniquely, and vice versa. Correspondingly, each anti-reflexive and symmetric binary relation corresponds to a tolerance relation uniquely. Therefore, in the isomorphism sense, there is no distinction between an anti-reflexive and symmetric binary relation and a tolerance relation.
Assume that 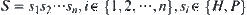 is an amino acid sequence. Protein
is an amino acid sequence. Protein 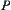 is obtained from the folding of S, and represented in 2D
is obtained from the folding of S, and represented in 2D 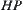 lattice model. For simplicity,
lattice model. For simplicity, 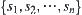 is indicated by
is indicated by 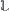 .
.
Definition 7.34
Define 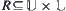 as
as  , or
, or 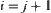 .
.
Definition 7.35
Define 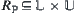 as
as  ,
, 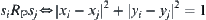 , where
, where  and
and 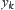 represent the horizontal and vertical coordinates of
represent the horizontal and vertical coordinates of 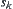 ,
, 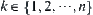 , in the 2D
, in the 2D 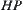 lattice model, respectively.
lattice model, respectively.
Binary relation 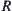 is an anti-reflexive and symmetric relation on
is an anti-reflexive and symmetric relation on 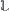 induced from
induced from 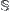 . It indicates the adjacency of two amino acids with respect to
. It indicates the adjacency of two amino acids with respect to 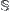 sequence, and is called a sequence adjacent relation. In the 2D
sequence, and is called a sequence adjacent relation. In the 2D 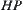 model, if and only if
model, if and only if 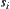 and
and 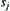 satisfy that one of their coordinates is equal and the difference of the other coordinates is 1 unit, then
satisfy that one of their coordinates is equal and the difference of the other coordinates is 1 unit, then 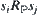 holds. Obviously,
holds. Obviously, 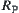 satisfies anti-reflexivity and symmetry, and is called a structure adjacent relation.
satisfies anti-reflexivity and symmetry, and is called a structure adjacent relation.
Now, we define a topology adjacent relation in 2D HP lattice model as follows.
Definition 7.36
Define 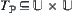 as
as  ,
, 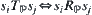 and
and 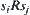 .
.
Obviously, the topology adjacent relation is the difference between the structure and sequence adjacent relations, as they can be regarded as a subset on  . In other words,
. In other words,  , where
, where 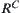 is a complement set of R.
is a complement set of R.
From the widely accepted assumption, the energy of primary state of a protein approaches the minimum. While in the 2D HP lattice model, the hydrophobic amino acids is required to concentrate in its center as far as possible after the folding. Assume that protein P is located in the 2D lattice model with length l and width m, after the folding of an amino acid sequence with length n. In the ideal situation, an amino acid is placed in each lattice point, and the hydrophobic ones are placed in the center lattice points as far as possible. Let 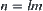 and
and 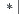 be the number of elements in set ‘
be the number of elements in set ‘ ’. Then,
’. Then, 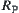 satisfies
satisfies
![]()
While
![]()
![]()
Since
![]()
![]() (7.17)
(7.17)
From 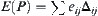 and the definition of
and the definition of 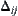 , if and only if
, if and only if 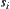 and
and 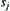 are topology adjacent,
are topology adjacent, 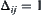 , otherwise
, otherwise 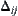 =0. Therefore, the Formula (7.17) is the estimation of the lower bound of
=0. Therefore, the Formula (7.17) is the estimation of the lower bound of 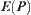 , i.e.,
, i.e., 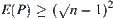 . The estimation does not eliminate topology adjacent that consists of amino acid pairs with P–P or H–P type. While the interaction among the amino acid pairs either with P–P type or H–P type is zero, and has no effect on the
. The estimation does not eliminate topology adjacent that consists of amino acid pairs with P–P or H–P type. While the interaction among the amino acid pairs either with P–P type or H–P type is zero, and has no effect on the 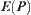 . The lower bound obtained above is not satisfactory. It’s known that only the topology adjacent amino acid pairs with H–H type play a part in
. The lower bound obtained above is not satisfactory. It’s known that only the topology adjacent amino acid pairs with H–H type play a part in 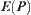 . In more ideal cases, the topology adjacent amino acid pairs with H–H type only appear on the rectangle
. In more ideal cases, the topology adjacent amino acid pairs with H–H type only appear on the rectangle 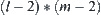 that within the rectangle lm. Now, the number of topology adjacent amino acids with H–H type is at most
that within the rectangle lm. Now, the number of topology adjacent amino acids with H–H type is at most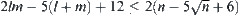 .
.
![]()
Let f be the number of amino acid pairs with H–H type in sequence  , including the head and the end amino acids of the sequence are H type. We have
, including the head and the end amino acids of the sequence are H type. We have
![]() (7.18)
(7.18)
This is also a lower bound estimation of  .
.
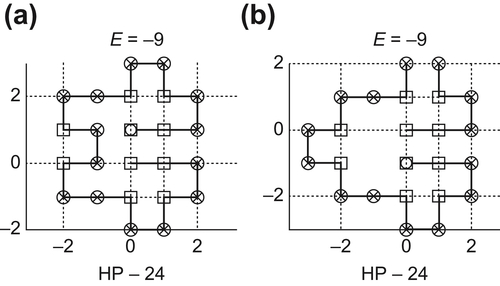
Fig. 7.7 shows the results that are obtained by the folding of HP benchmark sequences in Unger and Moult (1993) via genetic algorithms (GA). The results of the lower bound of energy obtained by genetic algorithms (GA) are shown in Table 7.1.
Table 7.1
The Results of the Lower Bound of Energy via GA
| Name | Length | Sequence | f | LB1 | LB2 | E |
| HP-20 | 20 | HPHP2H2PHP2HPH2P2HPH | 3 | -12 | invalid | -9 |
| HP-24 | 24 | H2P2(HP2)6H2 | 3 | -16 | 3-12=-9 | -9 |
| HP-25 | 25 | P2HP2 (H2P4)3H2 | 4 | -16 | 4-12=-8 | -8 |
| HP-36 | 36 | P3H2P2H2P5H7P2H2P4H2P2H P2 | 10 | -25 | 10-24=-14 | -14 |
| HP-48 | 48 | P2H (P2H2)2P5H10P6(P2H2)2HP2H5 | 17 | -36 | 17-40=-23 | -23 |
| HP-50 | 50 | H2(PH)3PH4P(PH3)3P(HP3)2HPH4(PH)4H | 17 | -48 | 17-41=-24 | -21 |

7.4.6. Conclusions
In the section, we extend the quotient space theory from the aspects of the structure and granulation of a domain. That is, further consider the structure produced by closure operations, and the granulation by tolerance relations. The domain structure plays an important role in quotient space theory, and also is one of the characteristics of the theory. With the help of the continuity of mappings and the connectivity of sets, we have the falsity-preserving property that is very useful in reasoning. The order relation is a specific topological structure. We pay attention to the order-preserving property that is also very useful in reality. Fortunately, these good properties still maintain under the expansion.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
