4.5. Operations and Quotient Structures
There is a variety of operations defined on a domain. In fact, an operation implicitly defines an interrelationship among elements of the domain. Under different grain-size worlds, the following issues should be answered. The induction of a corresponding operation on a quotient space from an operation defined on its original space, and the synthesis of two operations defined on different grain-size spaces becomes a new operation on their synthetic space, i.e. a finer space.
Let us consider two simple examples.
Example 4.10
Let ‘+’ be a common addition operation on X. Define an operation on 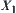 as follows.
as follows.
![]()
Let 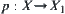 be a natural projection.
be a natural projection.
Obviously, for 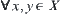 , we have
, we have 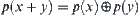 .
.
It implies that the projection of the sum ‘+’ of any two elements x and y on X is identical to the sum ‘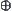 ’ of the projections of these two elements on
’ of the projections of these two elements on 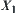 . Projection p with the preceding property is called a ‘homomorphism transform’ from
. Projection p with the preceding property is called a ‘homomorphism transform’ from 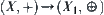 . Operation ‘
. Operation ‘ ’ can be regarded as an induced addition operation on
’ can be regarded as an induced addition operation on 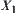 from the addition operation ‘+’ on X.
from the addition operation ‘+’ on X.
Unfortunately, there is not such an induced operation for many operations in general.
Example 4.11
Now we discuss operation ‘+’ on X. We show there does not have any induced operation ‘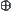 ’ on
’ on 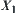 such that projection
such that projection  is homomorphic.
is homomorphic.
Proof
By reduction to absurdity, otherwise assume there is an induced operation 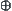 on X1.
on X1.
By taking  and
and  , from the homomorphism property of p we have
, from the homomorphism property of p we have
![]()
If taking  and
and 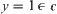 , then we have
, then we have
![]()
This is a contradiction, and hence there does not have to be any induced operation such that p is homomorphic.
However, in what conditions does a homomorphic-induced operation exist? In modem algebra, for some structures such as groups there are some related results. A result is given below as an example.
Example 4.12
X is a group, 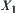 is a normal sub-group of X. Let
is a normal sub-group of X. Let 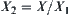 be a quotient group of X with respect to
be a quotient group of X with respect to 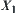 . An induced operation is defined on
. An induced operation is defined on 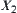 as follows.
as follows.
![]()
If p is a 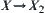 projection, then p is a homomorphism transformation.
projection, then p is a homomorphism transformation.
From the example, it is known that only under certain conditions can an operation with homomorphism property on a quotient space be induced.
Assume that N is an operation on X and  is a quotient space of X. If there exists an operation
is a quotient space of X. If there exists an operation 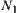 on
on 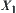 such that
such that 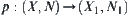 is a homomorphism projection, then
is a homomorphism projection, then 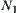 is said to be a quotient operation on
is said to be a quotient operation on 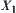 with respect to N, or simply a quotient operation.
with respect to N, or simply a quotient operation.
As mentioned before, generally, there is not a quotient operation on a quotient space. Similar to semi-order discussed in Chapter 1, we can adjust the quotient space by merging and refining approaches such that a corresponding quotient operation exists.
4.5.1. The Existence of Quotient Operations
X is a domain. 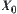 is the coarsest quotient space of X, namely, a quotient space regarding all elements of X as an equivalence class.
is the coarsest quotient space of X, namely, a quotient space regarding all elements of X as an equivalence class.
Assume that N is a binary-operation on X, namely
![]()
Given a quotient space 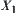 of X, obviously, we have
of X, obviously, we have 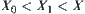 .
.
It is obvious that N has a corresponding quotient operation 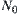 on
on 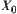 as long as we define
as long as we define  .
.
If there is not a quotient operation 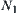 on
on 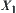 , the problem is whether the finest quotient space
, the problem is whether the finest quotient space 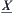 exists such that
exists such that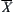 exists such that
exists such that
![]()
![]()
If such quotient operations exists, 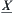 and
and 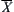 are operational lower and upper bound spaces of
are operational lower and upper bound spaces of 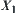 with respect to operation N, respectively,
with respect to operation N, respectively, 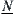 and
and  are lower and upper quotient operations of N corresponding to
are lower and upper quotient operations of N corresponding to 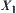 , respectively, or simply lower and upper quotient operations of
, respectively, or simply lower and upper quotient operations of 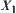 .
.
Obviously, if  , then
, then 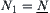 is a quotient operation on
is a quotient operation on 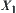 .
.
We next discuss the existence of upper and lower quotient operations.
Proposition 4.2
X is domain. N is a binary-operation on X. 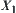 is a quotient space of X. There exist upper and lower quotient operations of N corresponding to
is a quotient space of X. There exist upper and lower quotient operations of N corresponding to 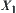 .
.
Proof
Let
![]()
![]()
Since 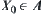 and
and 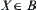 , i.e., A and B are non-empty, from Proposition 1.2 in Chapter 1, we know that all quotient spaces of X constitute a complete semi-order lattice according to the quotient inclusion relation. Therefore, there exist both the least upper bound space
, i.e., A and B are non-empty, from Proposition 1.2 in Chapter 1, we know that all quotient spaces of X constitute a complete semi-order lattice according to the quotient inclusion relation. Therefore, there exist both the least upper bound space  on A and the greatest lower bound space
on A and the greatest lower bound space 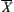 on B.
on B.
We only need to show there exist quotient operations on 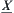 and
and 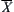 , respectively.
, respectively.
From the definition of the least upper bound space, we can see that for 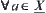 , there exists
, there exists 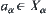 such that
such that 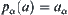 , where
, where 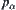 is the projection from
is the projection from 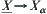 . Regarding
. Regarding  and
and  as sub-sets of X and
as sub-sets of X and 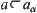 , we have
, we have 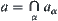 . As stated above, it is known that
. As stated above, it is known that 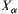 has a quotient operation
has a quotient operation 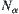 .
.
For 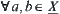 , let
, let 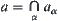 and
and 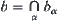 , where
, where 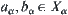 . From
. From 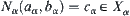 , letting
, letting 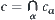 , since
, since 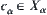 , we have
, we have 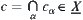 .
.
Define 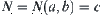 . Since
. Since 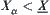 , then given
, then given 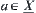 letting
letting  and
and 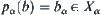 ,
, 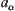 and
and 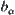 are unique. Therefore, c defined above is unique, namely,
are unique. Therefore, c defined above is unique, namely, 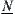 is uniquely defined.
is uniquely defined.
We next only need to prove that 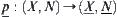 is homomorphic.
is homomorphic.
Let 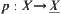 and
and  .
.
Since 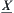 is the least upper bound space of
is the least upper bound space of 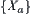 , we have that for
, we have that for  ,
,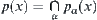 holds.
holds.
Given 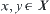 , let
, let  and
and 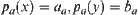 .
.
Assume 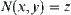 . Let
. Let 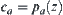 and
and 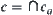 . Since
. Since 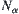 is a quotient operation, we have
is a quotient operation, we have 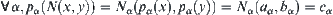 .
.
By intersection operation, we have
![]()
From the definition of  , we have
, we have 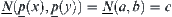 .
.
Finally, we can write
![]()
Namely, 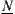 is a quotient operation on
is a quotient operation on 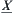 . In other words,
. In other words, 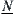 is a lower quotient operation of X1.
is a lower quotient operation of X1.
We now prove there is an upper quotient operation of X1.
Let 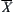 be the infimum of B. For
be the infimum of B. For 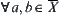 , let
, let
![]()
We now show that any two elements in d are 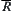 -equivalent, where
-equivalent, where  is an equivalence relation corresponding to
is an equivalence relation corresponding to 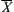 .
.
Given 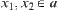 and
and 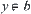 , let
, let 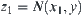 and
and  . Since
. Since 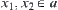 and
and 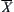 is the infimum of B, there exist
is the infimum of B, there exist 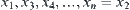 such that
such that
![]()
There is no lost generality in assuming that 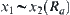 , we have
, we have
![]()
![]()
Since 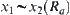 , we have
, we have 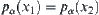 .
.
Thus, 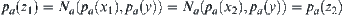 .
.
As 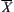 is the infimum of B, from the definition of infimum we obtain
is the infimum of B, from the definition of infimum we obtain 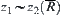 .
.
Similarly, for 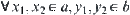 ,
, 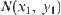 and
and 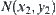 are
are  -equivalent.
-equivalent.
We conclude that any two of elements in d are 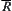 -equivalent.
-equivalent.
Let c be an equivalence class on 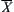 containing d. Define
containing d. Define 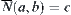 .
.
From the result above, c is uniquely defined and satisfies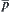 is a projection from
is a projection from 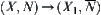 .
.
![]()
It follows that 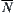 is an upper quotient operation of N with respect to
is an upper quotient operation of N with respect to 
4.5.2. The Construction of Quotient Operations
We have proved that for any quotient space there exist unique upper and lower quotient operations. Now we discuss the construction of them, namely, 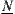 and
and 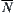 , when X, N and X1 are given, especially, if X is a finite set. In this section, X is assumed to be a finite set.
, when X, N and X1 are given, especially, if X is a finite set. In this section, X is assumed to be a finite set.
Lower Quotient Operation
N is a binary-operation on X. 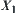 is a quotient space of X.
is a quotient space of X. 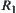 is an equivalence relation corresponding to
is an equivalence relation corresponding to 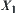 .
.
Define relation 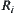 recursively as follows.
recursively as follows.
![]()
![]()
Let 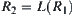 . Generally, define
. Generally, define 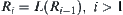 .
.
Since X is a finite set, there exists a minimal integer n such that 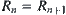 .
.
Let  be an equivalence relation with
be an equivalence relation with 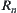 as its base. Namely,
as its base. Namely,
![]()
Let X be a quotient space with respect to 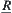 . For
. For 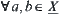 , let
, let
![]()
We next show that any two of elements in d are 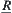 -equivalent.
-equivalent.
For 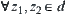 , there exist
, there exist 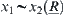 and
and  such that
such that 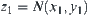 and
and  .
.
From the definition of 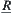 , there exist
, there exist  and
and 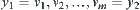 such that
such that  and
and 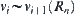 .
.
Letting  then
then 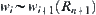 . Since
. Since 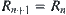 , have
, have 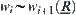 ,
,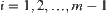 .
.
Especially, 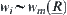 , hence
, hence 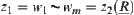 .
.
Namely, any two of elements in d are 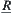 equivalent.
equivalent.
Let c be an equivalence class in X containing d. Hence c is an element of 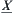 .
.
Define 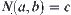 , from the definition, N is uniquely defined. Similar to Proposition 4.2, it can be proved that N is a quotient operation on
, from the definition, N is uniquely defined. Similar to Proposition 4.2, it can be proved that N is a quotient operation on  .
.
Finally, it only needs to show that 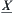 is the upper bound of a family of quotient spaces A defined in Section 4.5.1.
is the upper bound of a family of quotient spaces A defined in Section 4.5.1.
Suppose there exists a quotient operation 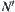 on space
on space 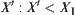 and
and 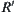 is an equivalence relation corresponding to
is an equivalence relation corresponding to  .
.
Since 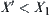 ,
,  . Namely, from
. Namely, from 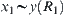 , we have
, we have 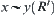 .
.
By induction, when i=1, 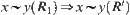 holds. Assuming that for
holds. Assuming that for 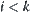
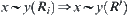 holds, we next show that for
holds, we next show that for 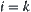 the conclusion holds as well.
the conclusion holds as well.
From 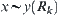 and based on the definition of relation
and based on the definition of relation 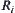 , we have two cases.
, we have two cases.
One is 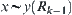 , and then we have
, and then we have 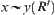 . Or there exist
. Or there exist 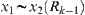 and
and  such that
such that 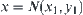 and
and  . Then
. Then 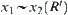 and
and 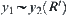 .
.
Since  is a quotient operation, we can write
is a quotient operation, we can write
![]()
That is, 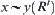 holds.
holds.
By induction, for any 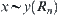 , we have
, we have  . Since
. Since 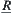 is an equivalence relation with
is an equivalence relation with  as its base, we have
as its base, we have 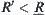 .
.
Therefore, X is the upper space of A. And N is the lower quotient operation of N with respect to 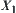 .
.
The above result is stated by the proposition below.
Proposition 4.3
X is a finite set. X1 is a quotient space of X. N is a binary-operation on X. The operation N defined as before is the lower quotient operation of X1, and X is the operational lower bound space of X1 with respect to N.
Example 4.13
Assume that 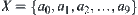 . Operation ‘+’ on X is defined as
. Operation ‘+’ on X is defined as
![]()
Let 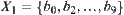 , where
, where 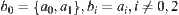 . Find the lower quotient operation and the lower bound space on
. Find the lower quotient operation and the lower bound space on 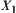 with respect to operation ‘+’.
with respect to operation ‘+’.
Solution
Let 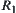 be an equivalence relation with respect to
be an equivalence relation with respect to 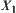 . Now we find
. Now we find 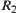 .
.
Since  , we have
, we have 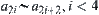 .
.
Similarly, 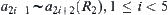 .
.
It is easy to know that 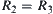 . Namely,
. Namely,
![]()
Operation 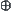 defined on
defined on 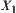 is as follows
is as follows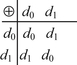
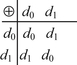
Upper Quotient Operation
X is a domain. N is a binary-operation on X. 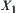 is a quotient space of X.
is a quotient space of X. 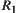 is an equivalence relation corresponding to
is an equivalence relation corresponding to  .
.
Define 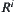 recursively as follows.
recursively as follows.
Let 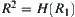
It is easy to show by induction that 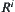 is an equivalence relation.
is an equivalence relation.
Generally, define 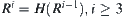 . Since X is finite, there exists a minimal integer
. Since X is finite, there exists a minimal integer  such that
such that 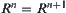 .
.
Let  .
. 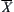 is a quotient space corresponding to
is a quotient space corresponding to 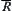 . Now we define an operation
. Now we define an operation 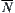 on
on 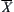 as follows.
as follows.
![]()
We first show that any two of elements in d are 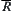 -equivalent.
-equivalent.
For 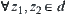 , assume that
, assume that 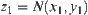 and
and 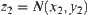 , where
, where 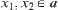 and
and 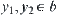 , namely,
, namely, 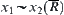 and
and 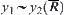 .
.
Since  we can write
we can write 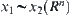 and
and 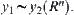
From the definition of 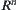 , it follows that
, it follows that 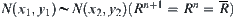 .
.
Namely, 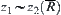 holds.
holds.
By letting c be an element of 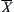 containing d, obviously c is uniquely defined by a and b.
containing d, obviously c is uniquely defined by a and b.
Define 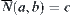 . We next show that
. We next show that 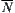 is a quotient operation on
is a quotient operation on 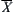 .
.
For 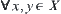 , letting
, letting 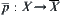 and
and 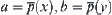 , then
, then 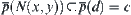 .
.
Moreover, 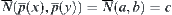 .
.
Since c is an element of  and
and 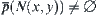 , then
, then 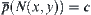 .
.
Thus, 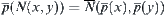 .
.
Finally, we show that quotient space 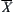 is the infimum of a family of quotient spaces B defined in Section 4.5.1.
is the infimum of a family of quotient spaces B defined in Section 4.5.1.
Given 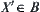 ,
, 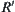 is its corresponding equivalence relation. Since
is its corresponding equivalence relation. Since 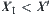
 , namely, for
, namely, for 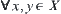 , if
, if 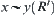 then
then 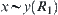 holds.
holds.
By induction on i, assuming that for i<k, if 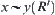 then
then 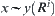 . We show next that the conclusion still holds for i=k.
. We show next that the conclusion still holds for i=k.
Assume that 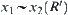 and
and 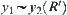 . From the induction assumption, for
. From the induction assumption, for 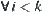 ,
, 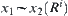 and
and 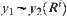 hold.
hold.
Since 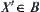 , there exists a quotient operation
, there exists a quotient operation 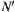 such that
such that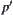 is a projection from
is a projection from 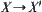 .
.
![]()
We have 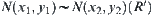 .
.
Similarly,  .
.
From the induction assumption, it is known that for k-1
![]()
From the definition of 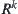 , obtain
, obtain 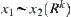 .
.
By induction, for 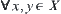 ,
, 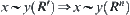 holds. Namely,
holds. Namely,  holds or
holds or 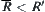 .
.
There is a quotient operation on 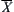 and
and  is the infimum of B. In other words,
is the infimum of B. In other words, 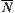 is the upper quotient operation on
is the upper quotient operation on 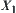 .
.
We have the following proposition.
Proposition 4.4
X is a finite set. X1 is a quotient set of X. N is a binary-operation on X. 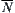 defined above, i.e.,
defined above, i.e., 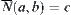 , is the upper quotient operation on X1 and
, is the upper quotient operation on X1 and  is the operational upper bound space of X1 with respect to N.
is the operational upper bound space of X1 with respect to N.
The approach for constructing 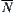 and
and 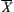 shown in Proposition 4.4 can be improved so that it is easy to be computed.
shown in Proposition 4.4 can be improved so that it is easy to be computed.
(X,N) is given, where X is a finite set. 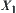 is a quotient space of X.
is a quotient space of X. 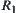 is an equivalence relation corresponding to
is an equivalence relation corresponding to 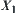 .
.
Let 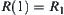 . Define a relation
. Define a relation 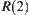 as follows.
as follows.
Let 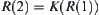 . Generally, define
. Generally, define 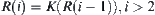 .
.
It is easy to prove that 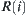 is an equivalence relation.
is an equivalence relation.
Since X is a finite set, there exists a minimal integer n such that  .
.
Let 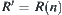 and
and 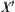 be a quotient space corresponding to
be a quotient space corresponding to 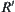 .
.
![]()
Let c be an equivalence class on 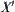 containing d
containing d
Define 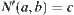 .
.
We have a proposition below.
Proposition 4.5
Under the definition and notations above,  is an operational upper bounded space of X1, and
is an operational upper bounded space of X1, and 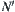 is an upper quotient operation of X1 with respect to N.
is an upper quotient operation of X1 with respect to N.
Proof
The proposition can be proved in much the same way as that in Proposition 4.4.
Note that definition 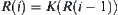 differs from definition
differs from definition 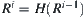 (see Section 4.5.2). The former is that for all
(see Section 4.5.2). The former is that for all  ,
,  and
and 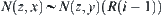 hold. However, the latter is that for all
hold. However, the latter is that for all  ,
, 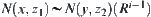 and
and  hold. Obviously, the former is a specific case of the latter. Therefore, finding
hold. Obviously, the former is a specific case of the latter. Therefore, finding 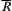 from
from 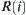 is much easier than from
is much easier than from 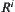 .
.
Note that instead of definition 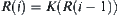 , we may use definition
, we may use definition 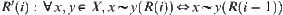 and for
and for 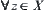 ,
, 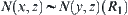 and
and 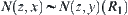 hold.
hold.
Assume that n is a minimal integer such that 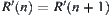 .
.
Let 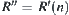 and
and  be a quotient space corresponding to
be a quotient space corresponding to 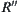 . We have the following property.
. We have the following property.
Property 4.1
For 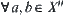 , letting
, letting 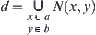 , we can see that
, we can see that 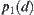 is an element of
is an element of  , where
, where 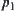 is a projection from X to
is a projection from X to 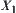 .
.
This property indicates that the result obtained from operation N on 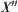 is uniquely defined on
is uniquely defined on 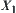 . Sometimes, for example in qualitative reasoning, it’s only needed that the quotient space rather than its quotient operation corresponding to N has such a property. Generally,
. Sometimes, for example in qualitative reasoning, it’s only needed that the quotient space rather than its quotient operation corresponding to N has such a property. Generally, 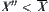 , sometimes it’s only needed to find
, sometimes it’s only needed to find 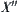 instead of
instead of 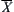 so that the computational complexity will be reduced.
so that the computational complexity will be reduced.
To illustrate the procedure of finding (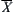 ,
,  ), we give an example below.
), we give an example below.
Example 4.14
Assume that 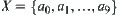 . Define an operation
. Define an operation 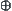 on X as
on X as
![]()
Let quotient space  . Find the upper quotient operation
. Find the upper quotient operation 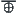 on
on 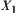 with respect to
with respect to 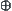 .
.
Solution
Let 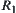 be an equivalence relation corresponding to
be an equivalence relation corresponding to 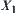 . Find
. Find 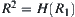 .
.
Let 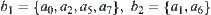 and
and  .
.
Since 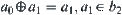 and
and 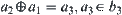 ,
, 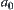 and
and  are not equivalent with respect to
are not equivalent with respect to  .
.
Similarly,  and
and 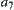 ,
, 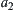 and
and 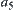 are not
are not 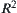 -equivalent. However,
-equivalent. However,  and
and 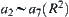 . Therefore,
. Therefore, 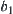 is decomposed into
is decomposed into 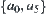 and
and 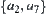 .
.
Similarly, it can be proved that  and
and  .
.
Finally, we have 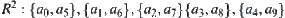 .
.
We observe that 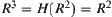 . Namely,
. Namely,  .
.
Let 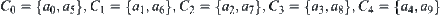 .
.
We have a quotient operation  on
on 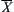 as follows.
as follows.

Note that since operation 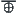 is commutative, the table above is symmetric.
is commutative, the table above is symmetric.
The above approach is only available when X is finite. When X is an infinite set, finding the upper (lower) quotient operation is more complicated. We next show some specific cases, i.e., X is a real set.
Quotient Operations on Real Quotient Spaces
X is a one-dimensional Euclidean space, i.e., real axis. Let quotient space 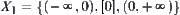 or simply
or simply  . This kind of quotient space is used in qualitative reasoning with numbers extensively (Murthy, 1988; William, 1988). We will discuss the structure of upper (lower) quotient operation of common ‘addition’ and ‘multiplication’ with respect to
. This kind of quotient space is used in qualitative reasoning with numbers extensively (Murthy, 1988; William, 1988). We will discuss the structure of upper (lower) quotient operation of common ‘addition’ and ‘multiplication’ with respect to 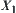 below.
below.
Common ‘addition’ on X is denoted by N. We find the upper (or lower) quotient operation of N with respect to 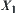 .
.
It’s obvious that the quotient space corresponding to the lower quotient operation N of N with respect to 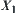 is
is 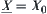 , i.e., the coarsest quotient space.
, i.e., the coarsest quotient space.
We now show that the quotient space corresponding to the upper quotient operation 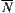 on
on 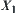 is
is  .
.
Assume that 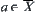 . If a contains more than one element of X, then assume that
. If a contains more than one element of X, then assume that 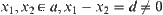 . Since
. Since  is a quotient operation, letting
is a quotient operation, letting 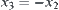 we have
we have
![]()
![]()
Namely, 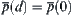 or
or  , where
, where  :
: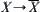 is a projection.
is a projection.
Since 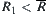 , we have
, we have 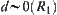 . But
. But 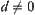 , this is a contradiction. Therefore, any element of
, this is a contradiction. Therefore, any element of 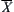 can only contain one element of X at most, i.e.,
can only contain one element of X at most, i.e.,  .
.
From the discussion above, unfortunately, the upper (lower) bound space with respect to  is the finest (coarsest) space. This is worthless. We will find a new way to solve the problem in the subsequent section.
is the finest (coarsest) space. This is worthless. We will find a new way to solve the problem in the subsequent section.
Now we discuss the quotient operation of common ‘multiplication’.
The common multiplication on X is denoted by  . We find the upper (lower) quotient operation of
. We find the upper (lower) quotient operation of 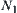 with respect to
with respect to 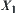 .
.
For simplicity, let 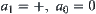 and
and 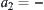 .
.
It is obvious that 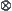 is a quotient operation on
is a quotient operation on 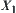 and satisfies:
and satisfies:
(1) 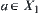 ,
,  thus
thus 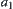 is an identity element on
is an identity element on  .
.
(2) 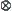 is commutative and associative, so an integral power of an element on
is commutative and associative, so an integral power of an element on 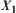 can be defined as follows.
can be defined as follows.
4.5.3. The Approximation of Quotient Operations
In the preceding section, we have shown that in the quotient space 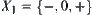 of real space X, the upper and lower space corresponding to ‘addition’ operation are the finest and coarsest ones, respectively. So the upper and lower quotient operations obtained are valueless in reality. But in qualitative reasoning with numbers, space
of real space X, the upper and lower space corresponding to ‘addition’ operation are the finest and coarsest ones, respectively. So the upper and lower quotient operations obtained are valueless in reality. But in qualitative reasoning with numbers, space 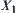 is widely used. We need to find a way to extricate ourselves from this predicament.
is widely used. We need to find a way to extricate ourselves from this predicament.
First let us see an example.
Example 4.15
A bathtub is shown in Fig. 4.8. 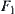 is the variation of input flow.
is the variation of input flow. 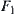 is the variation of output flow. H is the variation of gage height. We have
is the variation of output flow. H is the variation of gage height. We have
![]()
Let 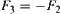 , we obtain
, we obtain 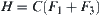 .
.
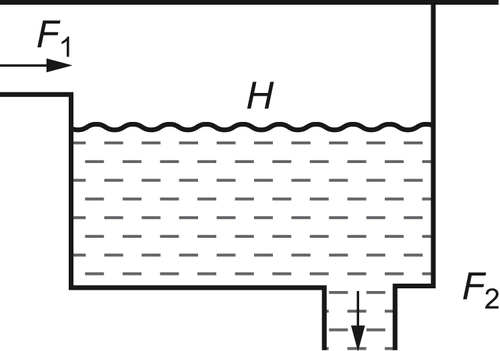
From the preceding formula, it is known that the sign of H can’t be determined exactly by the signs of 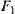 and
and 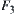 . Namely, we can’t judge the value of H exactly on quotient space
. Namely, we can’t judge the value of H exactly on quotient space  .
.
If 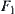 is fixed, for example,
is fixed, for example, 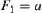 , then refining
, then refining 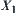 we have
we have 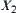 as follows
as follows
![]()
The elements of 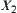 are denoted by
are denoted by 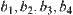 and
and 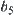 , respectively.
, respectively.
Hence, we have
![]()
In other words, if 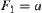 then the sign of H can be decided exactly by the variation of
then the sign of H can be decided exactly by the variation of 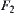 on
on 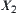 . Or the value of H on
. Or the value of H on 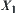 can be determined by the value of
can be determined by the value of 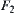 on
on 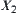 uniquely.
uniquely.
The example shows that under some given initial conditions, when we analyze a system at 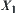 space, it is not necessary to find the upper (lower) quotient operation on
space, it is not necessary to find the upper (lower) quotient operation on 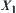 with respect to N. As long as
with respect to N. As long as 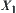 is properly refined, it can still meet the demand of a certain qualitative analysis.
is properly refined, it can still meet the demand of a certain qualitative analysis.
Two refinement approaches are given below.
Successive Refinement Method
N is a binary-operation on X denoted by 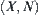 .
. 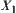 is a quotient space of X.
is a quotient space of X. 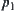 :
: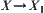 is a projection.
is a projection.
Define an operation on 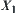 as follows. It is called a pseudo-quotient operation corresponding to N.
as follows. It is called a pseudo-quotient operation corresponding to N.
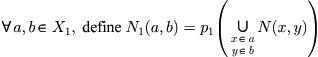
If in the right hand side of the formula, for  ,
, 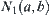 is an element of
is an element of 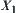 , then
, then 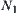 is a quotient operation on
is a quotient operation on 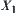 , otherwise
, otherwise 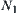 is a pseudo-quotient operation. Now transforming the problem represented at space
is a pseudo-quotient operation. Now transforming the problem represented at space 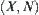 to space
to space 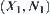 , if we find some results obtained from operation
, if we find some results obtained from operation 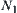 are not unique on
are not unique on 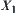 , for example,
, for example,  is not single value on
is not single value on 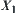 , then
, then 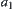 and
and 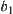 are refined. After refinement, if some results of operation
are refined. After refinement, if some results of operation 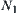 we are interested in are still not single-valued, the refining process continues until all results we needed are single-valued.
we are interested in are still not single-valued, the refining process continues until all results we needed are single-valued.
If a problem represented at space 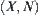 is deterministic, the refining process can go on until a proper space is obtained. If a problem represented at
is deterministic, the refining process can go on until a proper space is obtained. If a problem represented at 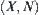 is not completely certain, the proper space may not be found.
is not completely certain, the proper space may not be found.
Let us see Example 4.15 again.
From 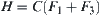 , when
, when 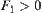 and
and 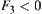 , we can see that the value of
, we can see that the value of 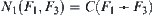 on space
on space 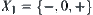 is not single-valued. The equivalence classes
is not single-valued. The equivalence classes 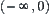 and
and 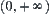 that
that  and
and  belong to must further be refined.
belong to must further be refined.
Generally, for the sum of 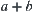 , if
, if 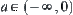 and
and 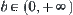 , then letting
, then letting  be an integer, intervals
be an integer, intervals 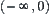 and
and 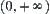 are divided into
are divided into 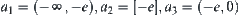 and
and 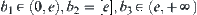 , respectively. Thus, the sum of
, respectively. Thus, the sum of 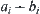 can be listed as follows.
can be listed as follows.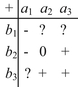
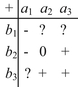
After refinement, only two out of nine combinations are uncertain. If the values that we are interested in are not contained in these two uncertain classes, we will have a proper space 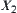 and in the space the sum ‘+’ can be uniquely defined. Otherwise, space
and in the space the sum ‘+’ can be uniquely defined. Otherwise, space 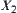 will further be decomposed.
will further be decomposed.
The deficiency of the method is that we don’t have a clear and definite criterion for judging what the proper refinement is needed.
Next, we give a successive approximation of the refinement method similar to the approach for finding  , when X is finite (see Propositions 4.4 and 4.5).
, when X is finite (see Propositions 4.4 and 4.5).
Successive Approximation
Given (X,N). 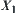 is a quotient space of X corresponding to
is a quotient space of X corresponding to 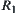 . Let
. Let 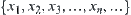 be a sequence of elements on X
be a sequence of elements on X
Define a relation 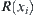 as follows
as follows
![]()
![]()
Generally, define
![]()
![]()
![]()
We show that 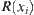 is an equivalence relation below.
is an equivalence relation below.
From induction on n, when n=1, for 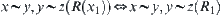 and
and 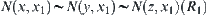 ,
, 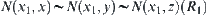 .
.
Since 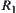 is an equivalence relation, we have that
is an equivalence relation, we have that 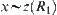 and
and 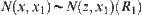 ,
, 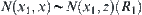 . Hence,
. Hence, 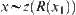 holds.
holds.
Namely, R(x1) is an equivalence relation.
Assuming that for 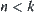 ,
, 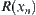 is an equivalence relation, we show that
is an equivalence relation, we show that 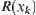 is also an equivalence relation.
is also an equivalence relation.
We only need to show that the transitivity of the relation holds.
Assume that  . From the definition of
. From the definition of 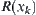 , we know that
, we know that 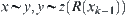 . Since
. Since 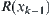 is an equivalence relation,
is an equivalence relation, 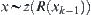 . Again from
. Again from 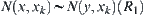 and
and 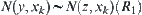 , we have
, we have 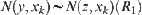 .
.
Similarly, 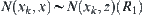 .
.
Therefore, 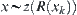 .
.
We obtain that 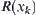 is an equivalence relation.
is an equivalence relation.
By induction, we conclude that 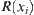 is an equivalence relation.
is an equivalence relation.
Let 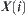 be a quotient space corresponding to
be a quotient space corresponding to 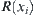 . Hence, the results obtained from operation N on any element in
. Hence, the results obtained from operation N on any element in 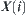 and one of elements
and one of elements 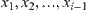 are unique. Namely, for
are unique. Namely, for 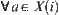 , by letting
, by letting 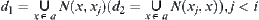 ,
,  or
or 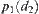 is an element of
is an element of  , where
, where 
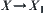 is a projection.
is a projection.
To a certain degree 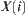 can be regarded as an approximation of
can be regarded as an approximation of 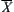 . Here, a sequence of elements
. Here, a sequence of elements 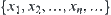 is selected in accordance with specific conditions, for example, the initial values. The deficiency of the method is that
is selected in accordance with specific conditions, for example, the initial values. The deficiency of the method is that 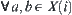 ,
,  may not be ensured to be single-valued on
may not be ensured to be single-valued on 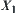 .
.
Since 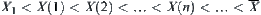 the successive approximation method is regarded as a refinement one as well.
the successive approximation method is regarded as a refinement one as well.
To show the refining process, we give a simple example.
Example 4.16
X is a real set. N is a common addition. 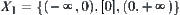 . Taking a sequence {–3, 2, 10, –8,…} of elements on X, find the successive approximation of N with respect to
. Taking a sequence {–3, 2, 10, –8,…} of elements on X, find the successive approximation of N with respect to 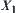 .
.
Solution
From 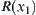 and
and 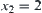 , we have
, we have
![]()
Similarly,
![]()
A sequence 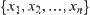 of elements on X is given. With
of elements on X is given. With 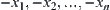 and zero as points of division, divide interval
and zero as points of division, divide interval 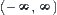 into (n+2) open sets. It’s easy to know that
into (n+2) open sets. It’s easy to know that 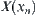 is just a quotient space composed by the corresponding (n+2) open sets and (n+1) points of division.
is just a quotient space composed by the corresponding (n+2) open sets and (n+1) points of division.
We summarize the methods for finding  ,
,  and the approximation of
and the approximation of 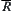 in Table 4.6, where X is a domain, N is a binary-operation on X,
in Table 4.6, where X is a domain, N is a binary-operation on X, 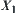 is a quotient space of X, and
is a quotient space of X, and 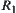 is its corresponding equivalence relation.
is its corresponding equivalence relation.
4.5.4. Constraints and Quotient Constraints
In many reasoning processes, we are confronted with a variety of constraints. Therefore, in a hierarchical reasoning process, the constraint propagation across different grain-size worlds must be considered.
The Definition of Constraints
Table 4.6
The formulas for finding ![]() and the approximation of
and the approximation of ![]()
| X is a finite set | Find | |
| Find | ||
| X is an infinite set | Given a set |

Definition 4.2
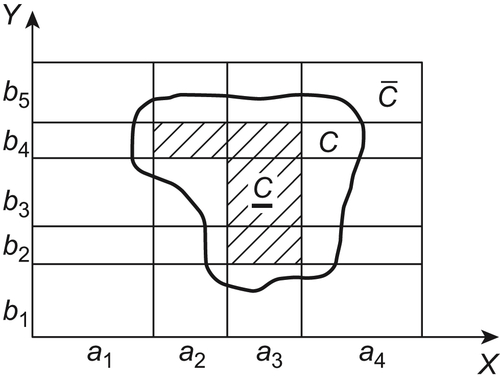
If C is a subset of a product space 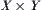 , then C is said to be a constraint on X and Y. When X=Y, C is simply called a constraint on X.
, then C is said to be a constraint on X and Y. When X=Y, C is simply called a constraint on X.
From the definition, it is known that a constraint C on X and Y is a relation on X and Y.
For  , let
, let 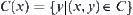 .
.
C(x) is said to be a section of C at x∈X.
Similarly, a section  of C at
of C at 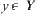 can be defined.
can be defined.
For example, 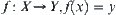 is a function.
is a function.
Letting 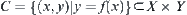 , then C is a constraint corresponding to function
, then C is a constraint corresponding to function 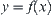 .
.
Again, given inequality 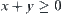 , by letting
, by letting 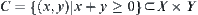 , then C is a constraint corresponding to
, then C is a constraint corresponding to 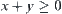 .
.
If N is a binary-operation on X, letting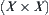 and X. In other words, an operation can be regarded as a constraint.
and X. In other words, an operation can be regarded as a constraint.
![]()
We next discuss the representations of constraints at different grain-size worlds.
Quotient Constraints
First, we consider the quotient space representation of a product space.
![]()
Definition 4.3
C is a constraint on X and Y. 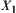 and
and 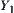 are quotient spaces of X and Y, respectively. Their corresponding equivalence relations are
are quotient spaces of X and Y, respectively. Their corresponding equivalence relations are 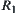 and
and 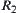 , respectively. Define
, respectively. Define
![]()
Example 4.17
When using 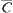 as a quotient constraint on quotient spaces
as a quotient constraint on quotient spaces 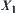 and
and 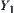 , the strong point is that the homomorphism principle is satisfied. Namely, if a problem on X has a solution satisfying constraint C, then the same problem on
, the strong point is that the homomorphism principle is satisfied. Namely, if a problem on X has a solution satisfying constraint C, then the same problem on 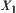 must have a solution satisfying constraint
must have a solution satisfying constraint 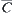 . If set
. If set 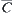 is much larger than C, under the weak constraint
is much larger than C, under the weak constraint 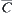 the solution on
the solution on 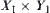 may not provide a useful cue for solving the same problem on X. Therefore, some stronger constraint
may not provide a useful cue for solving the same problem on X. Therefore, some stronger constraint 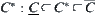 may be used to narrow the problem-solving space on X but it doesn’t guarantee the satisfaction of the homomorphism principle.
may be used to narrow the problem-solving space on X but it doesn’t guarantee the satisfaction of the homomorphism principle.
Example 4.18
In qualitative reasoning with numbers, Kuipers (1988) presented a concept of ‘envelope constraints’. We next show the relationship between his notion of ‘constraint’ and ours.
Assume that 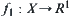 and
and 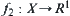 , where
, where 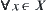 ,
, 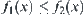 , and
, and 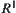 is a real set.
is a real set.
If 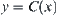 is a set-valued mapping from X to
is a set-valued mapping from X to 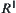 and satisfies
and satisfies is just the envelope constraint of x and y defined by Kuipers.
is just the envelope constraint of x and y defined by Kuipers. 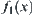 and
and 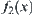 are called upper and lower envelopes, respectively and denoted by
are called upper and lower envelopes, respectively and denoted by 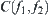 .
.
![]()
Let
![]()
From our definition, C is a constraint on X and  , and it’s just the envelope constraint
, and it’s just the envelope constraint  . It is obvious that the envelope constraint is a specific case of the constraint defined in this section.
. It is obvious that the envelope constraint is a specific case of the constraint defined in this section.
Kuipers also presented an envelope constraint propagation approach. We cite it here.
The upper and lower envelopes 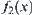 and
and 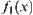 of the constraint between x and y are given as shown in Fig. 4.10. Let
of the constraint between x and y are given as shown in Fig. 4.10. Let 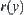 and
and 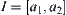 be the variation range of y and x, respectively. Now, we find the new variation range of x, when range
be the variation range of y and x, respectively. Now, we find the new variation range of x, when range  propagates across
propagates across 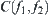 .
.
According to the envelope constraint propagation method, projecting the lower endpoint of 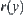 across envelope
across envelope 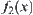 , we have a point b2 on X. Similarly, when projecting the upper endpoint of r(y) across envelope
, we have a point b2 on X. Similarly, when projecting the upper endpoint of r(y) across envelope  , we have
, we have 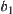 . Finally, we obtain an interval
. Finally, we obtain an interval 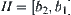 on X. Letting
on X. Letting  , we have
, we have 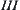 . This is a new variation range of X.
. This is a new variation range of X.
From our viewpoint, a quotient space of  is defined as
is defined as
![]()
Let
![]()
Finding the projection 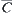 of C on
of C on 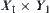 and the section
and the section  of
of 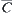 at
at 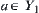 , we have
, we have 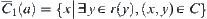 . Namely,
. Namely, 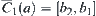 .
.
The section  indicates the variation range of x under the constraint C when
indicates the variation range of x under the constraint C when 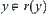 . By intersecting
. By intersecting  with
with  , we have an interval
, we have an interval  . This is the same as the variation range of x obtained by the Kuipers method. Therefore, the envelope constraint propagation presented by Kuipers is a specific example of the quotient constraint construction methods.
. This is the same as the variation range of x obtained by the Kuipers method. Therefore, the envelope constraint propagation presented by Kuipers is a specific example of the quotient constraint construction methods.
The Relationship of Constraints
Projection of Constraints
C is a constraint on X and Y. 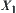 and
and 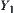 are quotient spaces of X and Y, respectively. Now, we find a constraint on
are quotient spaces of X and Y, respectively. Now, we find a constraint on 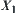 and
and 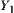 corresponding to C.
corresponding to C.
We have defined the equivalence relation corresponding to quotient space  of
of  . However, C is a subset of
. However, C is a subset of 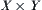 . The constraint on
. The constraint on 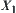 and
and 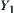 should be a subset of
should be a subset of 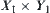 . Naturally, the induced constraint of C on
. Naturally, the induced constraint of C on 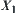 and
and 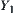 is defined as p(C), where p is a projection from
is defined as p(C), where p is a projection from 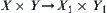 .
.
It is easy to know that 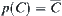 , where
, where 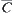 is the outer quotient constraint of C.
is the outer quotient constraint of C.
The combination of Constraints
![]()
If the combination constraint  is only expected to satisfy either
is only expected to satisfy either 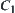 or
or 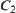 , then it’s denoted by
, then it’s denoted by
![]()
The Synthesis of Constraints
The synthesis of constraints 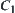 and
and 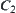 is defined as follows.
is defined as follows.
Let 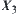 be the supremum of
be the supremum of 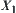 and
and 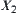 ,
, 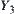 be the supremum of
be the supremum of 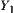 and
and 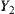 ,
, 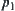 and
and 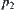 be the projections from
be the projections from 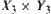 to
to  and
and 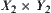 , respectively.
, respectively.
Let 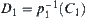 and
and 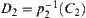 .
.
Define 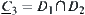 ,
, 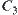 is said to be an inner synthetic constraint of
is said to be an inner synthetic constraint of 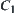 and
and 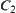 .
.
Define 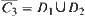 ,
, 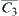 is said to be an outer synthetic constraint of
is said to be an outer synthetic constraint of 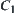 and
and 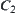 .
.
According to different situations, any 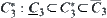 can be chosen as synthetic constraint of
can be chosen as synthetic constraint of 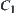 and
and 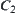 .
.
The synthesis of 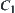 and
and 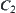 can also be constructed in much the same way as that stated in Chapter 3. To illustrate we show an example below.
can also be constructed in much the same way as that stated in Chapter 3. To illustrate we show an example below.
Example 4.19
X and Y are real sets. Lebesgue measures 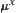 and
and 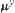 are defined on X and Y, respectively.
are defined on X and Y, respectively.
Let  and
and 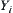 be quotient spaces of X and Y, respectively. Assume that each element of
be quotient spaces of X and Y, respectively. Assume that each element of 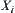 and
and  , i=1,2, is measurable on
, i=1,2, is measurable on 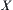 and
and 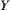 , respectively.
, respectively.
Let 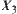 be the supremum space of
be the supremum space of 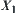 and
and 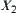 .
. 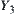 be the supremum space of
be the supremum space of 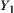 and
and 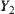 . Since all elements on
. Since all elements on 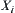 and
and 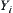 are measurable on X and Y, respectively, the elements of
are measurable on X and Y, respectively, the elements of 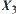 and
and 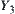 are measurable as well.
are measurable as well.
Let 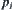 , i=1,2, be a projection from
, i=1,2, be a projection from 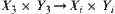 .
.
Assume that  is a measurable set on
is a measurable set on 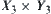 and satisfies
and satisfies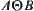 indicates the symmetric difference between A and B and is defined as
indicates the symmetric difference between A and B and is defined as
![]()
![]()
Namely, the synthetic constraint of 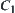 and
and  is defined as a set
is defined as a set 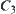 on
on 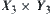 such that the sum of the measures of its symmetric differences with
such that the sum of the measures of its symmetric differences with 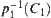 and
and  is minimum.
is minimum.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.

